文章编号: 1004-0609(2005)01-0049-06
镍基定向凝固高温合金力学性能的统计分析
郭运强, 张克实, 耿小亮, 刘 芹
(西北工业大学 力学与土木建筑学院, 西安 710072)
摘 要: 通过随机抽样和统计的方法对定向凝固高温合金的弹性常数进行了分析。 结果表明: 由于合金晶粒数目较少, 弹性常数统计结果的变异系数较大, 证实定向凝固高温合金横向性能分散性较大; 由抽样检验发现, 定向凝固高温合金的弹性常数统计上近似服从正态分布; 应该采用统计方法描述定向凝固合金的力学行为。
关键词: 定向凝固高温合金; 横观各向同性; 弹性常数; 正态分布 中图分类号: O344.6; TG113
文献标识码: A
Statistical analysis of mechanical behavior of nickle-base directionally solidified superalloy
GUO Yun-qiang, ZHANG Ke-shi, GENG Xiao-liang, LIU Qin
(School of Mechanics, Civil Engineering and Architecture,
Northwestern Polytechnical University, Xi'an 710072, China )
Abstract: Directionally solidified superalloys elastic constants were analyzed by employing statistical and random sampling methods. The results show that the coefficient of variation of elastic constants is fairly large because specimen has very few grains, which proves that the transverse elastic properties of directionally solidified superalloy present considerably scattered and satisfy normal distribution. The statistical analysis should be employed to describe directionally solidified superalloys mechanical behavior.
Key words: directionally solidified superalloy; transverse-isotropic; elastic constants; normal distribution
定向凝固高温合金已广泛应用于国内外航空发动机制作涡轮叶片和导向叶片。 定向凝固合金的结晶方向平行于零件的最大应力方向, 基本上消除了垂直于最大应力方向的横向晶界。 从材料结构上来说, 定向凝固合金是各向异性材料, 由于横截面内各晶粒取向随机分布, 目前的研究通常假设其为横观各向同性[1-4], 即横截面内为各向同性, 而结晶方向呈现不同的力学性能。 与将晶粒随机取向的多晶集合体简化为各向同性体的情形类似, 在晶粒数目足够多时这样的简化才具有合理性。 航空发动机定向凝固涡轮叶片只有几个或十几个晶粒[5, 6], 涡轮叶片的结构尺寸和晶粒尺寸几乎具有相同的数量级, 横观各向同性假设的合理性令人质疑。 通过单晶的性质来预测多晶集合体的宏观力学行为是一个较为直接而且有效的途径。 Buge等[7]研究了单个晶粒与多晶集合体弹性性质之间的关系。 在此基础上, Masatsugu等[8]利用自洽的方法研究了晶粒取向偏差与晶粒纵横比对柱状晶集合体弹性性质的影响。 张克实等[9]对定向凝固涡轮叶片进行了考虑晶粒结构的高温蠕变分析, 但只考虑了一种抽样结果, 没有做深入的统计分析。
以往的研究者[10-13]侧重于对定向凝固合金高温宏观力学性能的研究, 而对这类材料采用横观各向同性假设是否合理以及弹性常数分散性的问题一直未见报导。 为此, 本文作者以定向凝固高温合金DZ125为研究对象, 采用统计的分析方法, 研究了80个随机取向试样弹性常数Eij、 νij的数值模拟测试结果的统计分布规律。
1 数值模型
根据陈荣章等[6]的DZ125合金涡轮叶片金相腐蚀照片(见图1), 可以明显地看到并排的柱状晶粒, 晶粒的尺寸为2~4mm。 为了近似地模拟发动机涡轮叶片的力学性能, 作为初步的定性分析, 本文作者设计了一个尺寸为40mm×10mm×100mm的板试样(涡轮叶片的近似尺寸), 晶粒形状和排布方式仿照Jorn[14]的模型建立, 模型含有19个晶粒, 模型的晶粒排布和网格划分如图2所示。 19个晶粒在横截面内取向随机分布, 各晶粒[001]取向允许与结晶方向有不超过15°的偏差, 偏轴程度从0°到15°随机分布(同铸造的质量要求相一致)。 图3所示为柱状晶粒在横截面内随机取向的示意图。

图1 DZ125合金涡轮叶片(已显露晶粒)
Fig.1 Turbine blade of DZ125 alloy

图2 模型的晶粒排布和网格划分
Fig.2 Grains arrangement and mesh of model
利用单轴拉伸实验测定材料的弹性常数。 测量 [001]取向材料参数时, 采用位移加载。 z=0平面上, z方向位移w=0, z=100平面上, w=0.01, 即在[001]取向上试样拉伸0.01%的应变。 材料变形过程中, 保证x=0、 y=0、 z=100, 3个平面始终保持为平面, [100]、 [010]取向测量时, 采用与此类似的加载方式。
2 横观各向同性假设
定义3轴为结晶轴, 1轴和2轴位于横截面上, 当采用横观各向同性假设时, 材料在横截面内为各向同性。 由于假设E1=E2, ν12=ν21, ν31=ν32, ν13=ν23, ν13/E1=ν31/E3, G13=G23, 故横观各向同性的应力应变关系可以表示为

式中 剪切模量G12不是独立的, 它可以用1, 2平面内的弹性模量E1和泊松比ν12表示:
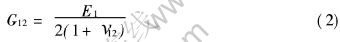
因此, 式(1)中只有E1、 ν12、 ν13、 E3和G13 5个独立的弹性常数。

图3 横截面的晶粒形状和取向分布示意图
Fig.3 Grains shape and orientation distribution of cross section
3 晶粒材料常数的确定
以定向凝固高温合金DZ125为研究对象, 其晶粒为面心立方结构(FCC), 因此沿3个材料主轴方向(晶体轴)具有相同的性质(只有E、 ν、 G 3个独立常数), 由于缺乏晶粒的材料参数, 作者取DZ125合金纵向测得的常数E、 ν、 G作为晶粒的弹性常数, E=127GPa, ν=0.410, G=107GPa[4]。
作者对该取法的合理性进行了验证。 当柱状晶粒的弹性常数取表1所列的值时, 采用图2所示的几何模型进行验算, 得到了表1中矩形试样的弹性常数(不考虑晶粒偏轴)。 由此可以看出, 两者的差别几乎可以忽略不计, 验算结果表明, 可以用DZ125纵向测得的弹性常数作为其单晶晶粒的弹性常数。
表1 [001]取向的弹性常数的验算结果
Table 1 Calculated computations result of elastic contants along [001]

4 结果与讨论
由于定向凝固合金制取工艺复杂, 且合金成分含有铪、 钽等贵重元素, 合金成本较高[12], 目前还不能用大量实验的方法来获得材料常数的分布规律, 而采用数值模拟的方法, 可以对铸造过程中的晶粒取向随机性对结果的影响进行模拟分析。 即通过改变随机取向来模拟实验中随机抽取的试样, 然后利用有限元分析对随机取向定向凝固合金试样做大量的模拟拉伸实验, 这一方法可以解决实验中泊松比不易测量的难题。
对80个随机试样的材料性能的统计结果如表2所示。 材料常数的平均值与材料手册[4]给出的实验值差别不大, 但横向性能的统计变异系数(标准差与平均值之比)要比[001]方向的大得多, 表明结果的分散性较大。 这些结果中ν12、 ν21变异系数最大。 从表2还可以看出, 弹性常数的最值与其实验值差别较大, 因此, 若用按平均方法得到的横观各向同性材料常数去分析某一个随机的试样, 会得出误差较大的结果。
图4分别给出了ν12、 ν13、 E1、 ν21、 ν23、 E2、 ν31、 ν32、 E3的分布规律, 并用正态分布曲线进行了拟合。 由图可以看出, DZ125合金抽样测得的弹性常数趋近于正态分布。 由于统计结果的标准差较大, 对定向凝固合金力学行为的描述应考虑采用统计方法进行评估。
需要指出的是, 横观各向同性假设的引入还会带来应力分布估计的误差。 如果材料满足横观各向同性假设, 则[001]方向拉伸时, 材料的横截面上的拉伸应力应该相同。 图5所示为材料的应力分量分布云图, 由图可以看出, 单向拉伸实验时, 横截面上拉伸应力的分布不再均匀, 拉伸应力从12~15MPa不等, 在各个晶粒之间应力的偏差高达25%。 应力的最值发生在三叉晶界附近,并且在晶界处有较大的应力梯度, 与Tvergaard等[15]的结论相一致。
表2 材料常数的统计结果(80个随机试样)
Table 2 Statistical analysis of elastic constants from 80 random specimens


图4 材料常数的统计结果
Fig.4 Statistical analysis of material constants

图5 材料的应力分量分布云图([001]方向拉伸)
Fig.5 Contour of stress component (tensile along [001])
5 结论
1) 对仅有十几个晶粒的定向凝固合金DZ125而言, 其横向弹性常数是分散的, 且近似服从正态分布。 对定向凝固合金力学行为的描述, 应考虑采用统计方法来进行评估。 若用平均的横观各向同性材料常数对某一个随机的试样进行力学分析, 结果与实际情形会有较大的误差。
2) 定向凝固合金DZ125宏观试样与其柱状单晶晶粒(立方对称)在[001]取向具有相同的弹性性能, 因此在数值计算中可以用定向凝固合金柱晶的纵向弹性常数作为其单晶晶粒的弹性常数。
3) 由于定向凝固材料横向弹性常数的分散性, 在实验中精确测得材料横向弹性常数的分布规律困难较大, 而数值模拟可以弥补这一缺陷, 能较为方便且较精确地得出其分布规律。
REFERENCES
[1]Zhang W F, Li Y J. Recrystallization and fatigue failure of DS alloy blades[EB/OL]. Http://www.sciencedirect.com.
[2]饶寿期, 田爱梅, 岳彦芳. 定向结晶气冷涡轮叶片应力分析[J]. 航空动力学报, 1994, 9(1): 122-126.
RAO Shou-qi, TIAN Ai-mei, YUE Yan-fang. DS air-cooled turbine blade stress analysis[J]. Journal of Aerospace Power, 1994, 9(1): 122-126.
[3]张谦琳, 周劲林. 定向结晶合金材料全部工程弹性常数的超声测定[J]. 实验力学, 1997, 12(4): 506-512.
ZHANG Qian-lin, ZHOU Jin-lin. Determination of all engineering elastic constants for an orientational crystalline alloy with ultrasonic method[J]. Journal of Experimental Mechanics, 1997, 12(4): 506-512.
[4]《中国航空材料手册》编辑委员会. 中国航空材料手册(第2卷)[M]. 第2版. 北京: 中国标准出版社, 2003.
Editorial Board of China Aeronautical Materials Handbook. China Aeronautical Materials Handbook (Vol. 2) [M]. 2nd ed. Beijing: China Standard Press, 2003.
[5]岳珠峰, 吕震宙. 晶体塑性理论在定向结晶材料与构件上的应用[J]. 中国机械工程, 1999, 10(1): 64-66.
YUE Zhu-feng, LU Zheng-zhou. The application of crystallographic theory on the directionally solidified materials and structures[J]. China Mechanical Engineering, 1999, 10(1): 64-66.
[6]陈荣章, 佘力, 张宏炜. DZ125定向凝固高温合金的研究[J]. 航空材料学报, 2000, 20(4): 14-19.
CHEN Rong-zhang, SHE Li, ZHANG Hong-wei, et al. Investigation of directionally solidified alloy DZ125[J]. Journal of Aeronautical Materials, 2000, 20(4): 14-19.
[7]Bunge H J, Kiewel R, Reinert T, et al. Elastic properties of polycrystals influence of texture and stereology[J]. Journal of the Mechanics and Physics of Solids, 2000, 48(1): 29-66.
[8]Masatsugu Y, Esteban P B. On the accuracy of self-consistent elasticity formulations for directionally solidified polycrystal aggregates[J]. International Journal of Solids and Structure, 2005, 42(3): 1073-1089.
[9]张克实, 杨士杰, 周柏卓. 定向凝固涡轮叶片的晶体热粘塑性变形与损伤分析[J]. 航空动力学报, 2004, 19(6): 762-770.
ZHANG Ke-shi, YANG Shi-jie, ZHOU Bai-zhuo. Crystalline thermo visco-plastic deformation and damage of directionally solidified turbine blade[J]. Journal of Aerospace Power, 2004, 19(6): 762-770.
[10]张国栋, 刘绍伦, 何玉怀, 等. 定向合金DZl25热/机械疲劳寿命预测模型评估[J]. 航空动力学报, 2004, 19(1): 17-22.
ZHANG Guo-dong, LIU Shao-lun, He Yu-huai, et al. Life predication of thermomechanical fatigue in DS superalloy DZ125[J]. Journal of Aerospace Power, 2004, 19(1): 17-22.
[11]袁超, 郭建亭, 杨洪才. 定向凝固镍基高温合金的高温恒载拉伸蠕变行为[J]. 中国有色金属学报, 1998, 8(S2):202-205.
YUAN Chao, GUO Jian-ting,YANG Hong-cai. Deformation mechanism for high temperature creep of a directionally solidified nickel-base superalloy[J]. The Chinese Journal of Nonferrous Metal, 1998, 8(S2):202-205.
[12]戴福隆, 尚海霞, 林国松, 等. 定向结晶材料高温蠕变规律研究[J]. 力学学报, 2002, 34(2): 186-191.
DAI Fu-long, SHANG Hai-xia, LIN Guo-song, et al. Study of high temperature creep deformation for crystallizing materials[J]. Acta Mechanica Sinica, 2002, 34(2): 186-191.
[13]谭检秀, 聂景旭. 定向凝固高温合金涡轮冷却叶片的热应力分析[J]. 航空学报, 1991, 12(7): 428-430.
TAN Jian-xiu, NIE Jing-xu. Thermal stress analysis on turbine cooling blade mode from orient clotting high temperature alloy[J]. Acta Aeronautica et Astronautica Sinica, 1991, 12(7): 428-430.
[14]Jorn H. A crystallographic model for the study of local deformation processes in polycrystals[J]. International Journal of Plasticity, 1999, 15(6): 605-624.
[15]Tvergaard V, Hutchinson J W. Microcracking in ceramics induced by thermal expansion or elastic anisotropy[J]. Journal of the American Ceramic Society, 1988, 71(3): 157-166.
基金项目: 国家自然科学基金资助项目(10472092); 航空基础科学基金资助项目(04C53027)
收稿日期: 2004-06-09; 修订日期: 2004-10-08
作者简介: 郭运强(1978-), 男, 博士研究生.
通讯作者: 郭运强, 博士研究生; 电话: 029-88493431; 传真: 029-88493468; E-mail:yefengnpu@163.com
(编辑李向群)