四肢缀条轴压钢管混凝土格构柱承载能力分段合成法
周旺保,蒋丽忠
(中南大学 土木工程学院,湖南 长沙,410075)
摘要:采用泰勒级数作为分段插值函数,在考虑多个截面的平衡条件和紧箍效应钢管混凝土应力-应变关系、剪切变形及初弯曲影响的基础上,建立杆件截面的平衡方程,提出四肢缀条轴压钢管混凝土格构柱弹塑性极限承载力数值方法,并编制相应的计算程序。利用提出的计算方法和编制的程序对国内已有轴压四肢钢管混凝土格构柱试件进行计算,并与现有一些规程进行比较。同时,结合数值计算结果及长细比折减系数计算模型,提出长细比折减系数计算公式。利用提出的长细比折减系数计算公式对国内已有轴压四肢钢管混凝土格构柱试件进行计算,并与数值计算结果及试验结果进行比较。研究结果表明:该方法适用于轴压长柱和短柱的弹塑性极限承载力的计算。规程计算方法结果偏于保守,计算误差大,本文方法的计算结果与试验结果较吻合;本文提出的长细比折减系数计算公式正确。
关键词:极限承载能力;轴心受压;钢管混凝土;格构柱;初弯曲
中图分类号:TU398.9;TU312;TU973+.2 文献标志码:A 文章编号:1672-7207(2011)07-2063-08
Piecewise synthesis method of bearing capacity on axial compressed four-tube concrete-filled steel tubular laced column
ZHOU Wang-bao, JIANG Li-zhong
(School of Civil Engineering, Central South University, Changsha 410075, China)
Abstract: Based on the equilibrium condition of several sections, the stress-strain relationship of the concrete-filled steel tube under the effect of confinement and the influence of the initial bending and shear, the equilibrium equation of the section was established. At the same time, the numerical method for calculating the elastic-plastic ultimate loads of the concrete-filled tubular laced columns was presented by adopting the Taylor’s series as the piecewise interpolation function and the corresponding computer program was compiled. Some axial compressed four-tube concrete-filled steel tubular laced columns were computed using the numerical method and the program, and the results were compared with the calculation results of some existing codes. The calculation formula of slender ratio reduced coefficient was proposed combining numerical calculation results and the slender ratio reduced coefficient model. The calculation results were compared with the numerical calculation results and the test results. The results show that this method is suitable for the elastoplasticity ultimate bearing capacity calculation of the long and short axial compressed columns. The code computational methods are conservative, the computational errors are great, and the computed results in this article agree well with the test results. The rationality of slender ratio reduced coefficient calculation formula has been attested.
Key words: ultimate bearing capacity; axial compression; concrete-filled steel tube; latticed column; initial bending
钢管混凝土构件具有承载能力强、塑性和韧性好、施工方便快捷、耐火性好以及造价经济合理等优点,近年来在房屋和桥梁结构中得到广泛的应用。而钢管混凝土格构式柱能以较小直径的柱肢取得较大的截面抗弯刚度,且柱肢以受轴压力为主,充分发挥了钢管混凝土柱受压强度大的特性和优势,因此,被大量应用于荷载偏心率较大或长细比较大的结构中,如单层工业厂房的柱子、设备构架柱、地铁站台柱、送变电杆塔、钢管混凝土拱桥、高层和超高层建筑结构等。目前国内外对单肢钢管混凝土柱的研究非常深入[1-11],并形成了相应的设计规程[4-6],而对于钢管混凝土格构柱的研究并不多,目前在格构柱设计上参照《钢结构设计规范GB 50017—2003》[12]。该规范将钢管混凝土格构柱比拟成钢格构柱的计算方法,没有考虑剪切变形的影响,也没有反映钢管混凝土柱肢的抗压强度和抗拉强度有重大差异这一特点。陈宝春等[13-17]对格构柱极限承载力进行了系列试验研究并提出了近似计算公式,试验结果表明:比拟计算方法精确度较低,计算值与试验值存在着较大误差。同时,在轴心压力作用下,不存在理想的轴压构件,在实际工程中构件常常带有微小的初始缺陷,对格构柱力学性能有影 响,因此,对轴压钢管混凝土格构柱进行深入的理论分析,提出较为精确的数值计算方法非常必要。本文作者在考虑构件剪切变形和初始缺陷影响基础上,提出了四肢缀条钢管混凝土格构柱长柱和短柱轴压极限承载力分段合成数值计算方法,同时编制了相应的计算程序,并将计算结果与现有规程计算方法以及现有的试验结果进行了比较,从而验证了本文数值计算方法的正确性,最后在分析大量数值计算结果的基础上提出了较为精确的钢管混凝土格构柱轴压极限承载力的计算公式。
1 基本假设
为简化分析,可对四肢缀条钢管混凝土格构柱进行如下假设:
(1) 格构柱达到极限承载力前柱肢不发生局部失稳,钢管和混凝土黏结良好,两者之间无相对滑移现象。
(2) 可假设在加载过程中,钢管混凝土截面和柱肢截面始终保持平面,钢管形状和面积始终保持不 变[14]。
(3) 外层钢管和核心混凝土的应力-应变关系为分段多项式。
(4) 缀条与柱肢组成桁架体系,即缀条与柱肢铰接。
(5) 假设格构柱达到极限荷载前缀条仍处于弹性阶段,即缀条在横向剪力作用下处于弹性阶段[14]。
(6) 柱子破坏时仍然为小挠度,既采用小挠度计算理论。
(7) 假设初弯曲曲线为挠度为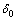 的半波正弦曲线,即
的半波正弦曲线,即
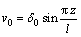
式中:v0为杆件的变形挠度;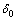 为杆件中截面初始挠度;l为杆件长度;z为杆件坐标。
为杆件中截面初始挠度;l为杆件长度;z为杆件坐标。
2 钢管及核心混凝土的应力与应变关系
2.1 钢管的应力与应变关系
钢管应力-应变关系[1]的表达式如下。
弹性段:
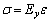 , 0≤ε≤εe1
, 0≤ε≤εe1
屈服段:
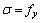 , εe1≤ε≤εe2
, εe1≤ε≤εe2
强化段:
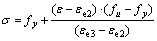 , εe2≤ε≤εe3
, εe2≤ε≤εe3
二次塑流段:
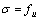 , ε≥εe2
, ε≥εe2
式中: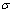 为钢管应力;
为钢管应力;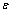 为应变;Ey为钢材弹性阶段的弹性模量;εe1为弹性极限应变;fy和fu分别为钢材的屈服强度和极限强度;取屈服极限应变εe2=10εe1;强化极限应变εe3=100εe1;钢材极限强度fu=1.6fy。
为应变;Ey为钢材弹性阶段的弹性模量;εe1为弹性极限应变;fy和fu分别为钢材的屈服强度和极限强度;取屈服极限应变εe2=10εe1;强化极限应变εe3=100εe1;钢材极限强度fu=1.6fy。
2.2 核心混凝土的应力-应变关系
核心混凝土应力-应变关系参考文献[3],其具体的表达式如下。
受压区:

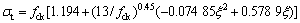
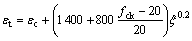

式中:套箍系数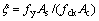 ;
;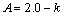 ;
;
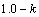 ;
;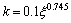 ;
;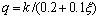 ;
;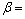
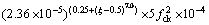 ;As和Ac分别为钢管和混凝土的截面积;fy为钢材的屈服强度;fck为混凝土的抗压强度;εc为普通混凝土应力-应变关系曲线峰值点对应的应变;εt和σt分别为核心混凝土应 力-应变关系曲线第1段与第2段交接点的应变和 应力。
;As和Ac分别为钢管和混凝土的截面积;fy为钢材的屈服强度;fck为混凝土的抗压强度;εc为普通混凝土应力-应变关系曲线峰值点对应的应变;εt和σt分别为核心混凝土应 力-应变关系曲线第1段与第2段交接点的应变和 应力。
受拉区:
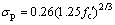
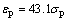
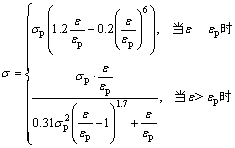
式中: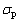 为混凝土峰值拉应力;
为混凝土峰值拉应力;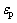 为混凝土峰值拉应变;
为混凝土峰值拉应变;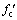 为混凝土圆柱体抗压强度;
为混凝土圆柱体抗压强度;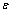 为混凝土应变。
为混凝土应变。
3 考虑压杆初弯曲和剪切变形的截面平衡方程
3.1 附加弯矩引起的压杆曲率公式推导
以斜缀条同向布置的四肢钢管混凝土格构柱的一半即双肢格构柱为例进行分析,四肢格构柱的承载力为则双肢格构柱承载力的2倍。受力分析如图1所示。
结合假设(6)及文献[15]可知:压杆剪力为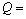
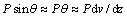 。剪力Q使压杆产生剪切挠曲v1;附加弯矩使压杆产生弯曲挠曲v2。因此,压杆的变形挠曲为v1+v2[18];由假设(7)可知压杆初始挠曲为v1,因此,压杆的总挠曲为v=v0+v1+v2[15](如图1所示)。由图1所示的受力分析可知压杆剪切应变为:
。剪力Q使压杆产生剪切挠曲v1;附加弯矩使压杆产生弯曲挠曲v2。因此,压杆的变形挠曲为v1+v2[18];由假设(7)可知压杆初始挠曲为v1,因此,压杆的总挠曲为v=v0+v1+v2[15](如图1所示)。由图1所示的受力分析可知压杆剪切应变为:
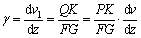 (1)
(1)
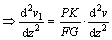 (2)
(2)
式中:γ为压杆剪切应变;P为压力;θ为截面转角;G为压杆等效剪切模量;K为考虑剪应力沿压杆横截面分布不均匀的系数,对于圆形截面K=1.11,对于矩形截面K=1.12,对于工字形截面K=2;F为压杆柱肢等效横截面面积。
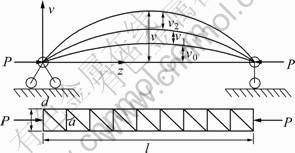
图1 受力分析图示
Fig.1 Analysis of force
压杆截面弯矩平衡微分方程为:
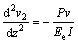 (3)
(3)
式中:Ee为考虑紧箍效应的钢管混凝土等效割线模量;I为压杆的等效惯性矩。
将式(2)和(3)相加得:
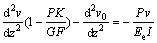 (4)
(4)
将初始挠曲表达式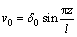 代入上式得:
代入上式得:
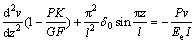 (5)
(5)
比较式(3)和(5)可得附加弯矩引起的压杆曲率公式为:
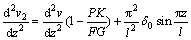 (6)
(6)
当压杆斜缀条反向布置时,单位剪力产生的剪应变[7]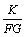 为:
为:
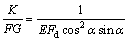 (7)
(7)
当压杆斜缀条同向布置时,单位剪力产生的剪应变[7]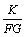 为:
为:
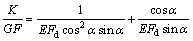 (8)
(8)
式中: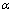 为压杆斜缀条与平缀条的夹角;E为压杆斜缀条弹模;Fd为压杆斜缀条横截面积。
为压杆斜缀条与平缀条的夹角;E为压杆斜缀条弹模;Fd为压杆斜缀条横截面积。
3.2 压杆截面平衡方程的推导
同样以斜缀条同向布置的四肢钢管混凝土格构柱的一半即双肢格构柱为例来进行分析,四肢格构柱的承载力为双肢格构柱承载力的2倍。对压杆各柱肢截面进行单元划分后(见图2)可得:
压力较大侧柱肢的抗力为:
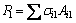 (9)
(9)
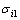 由
由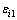 确定,
确定,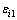 由下式确定:
由下式确定:
 (10)
(10)
由式(6)得:
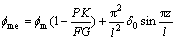 (11)
(11)
式中: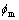 为压杆总曲率;
为压杆总曲率;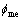 为压杆附加弯矩产生的弯曲曲率;d为压杆两柱肢重心间距离;
为压杆附加弯矩产生的弯曲曲率;d为压杆两柱肢重心间距离;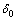 为压杆中截面初始挠度;Ai1为压力较大侧柱肢截面划分单元面积;yi1为压力较大侧柱肢截面划分单元中心到压杆截面中心的距离;ε0为压杆截面中心应变;εi1为压力较大侧柱肢截面划分单元的应变;应力σi1由εi1及第2节所介绍的应力应变关系确定。
为压杆中截面初始挠度;Ai1为压力较大侧柱肢截面划分单元面积;yi1为压力较大侧柱肢截面划分单元中心到压杆截面中心的距离;ε0为压杆截面中心应变;εi1为压力较大侧柱肢截面划分单元的应变;应力σi1由εi1及第2节所介绍的应力应变关系确定。

图2 截面单元划分及条带应变计算
Fig.2 Element and strain calculation of cross-section
对于斜缀条同向布置的压杆,由式(8)可知:
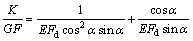
压力较小侧柱肢的抗力为:
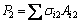 (12)
(12)
σi2由εi2确定,εi2由下式确定:
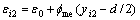 (13)
(13)
式中:Ai2为压力较小侧柱肢截面划分单元面积;yi2为压力较小侧柱肢截面划分单元中心到压杆截面中心的距离;εi2为压力较小侧柱肢截面划分单元的应变;应力σi2由εi2及第2节所介绍的应力应变关系确定。
由压杆截面内外力平衡得:
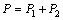 (14)
(14)
压杆截面抵抗弯矩为:
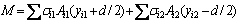 (15)
(15)
由压杆截面内外弯矩平衡得:
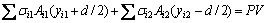 (16)
(16)
当斜缀条反向布置时,式(11)中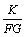 为:
为:
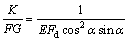
其他计算过程与斜缀条平行布置的计算过程一样。对于其他缀条布置形式亦进行相似的处理。
4 数值计算的实现
4.1 数学迭代公式
构件长度单元划分如图3所示。取迭代公式如 下[15]:
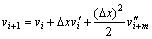 (17)
(17)
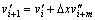 (18)
(18)
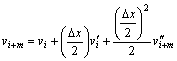 (19)
(19)
式中:vi表示第i微段右端点总挠度;?x表示微段长度;vi+m在计算过程中以第i+1段的中点总挠度代替。
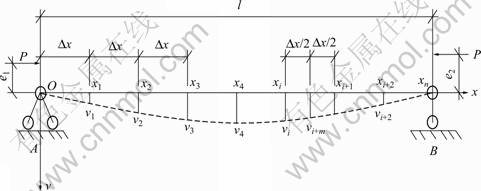
图3 构件长度单元划分
Fig.3 Length units’division of components
4.2 单肢短柱极限承载力
若有格构柱单肢短柱极限承载力试验值,则以试验值为准;若无试验值,则格构柱单肢短柱极限承载力按以下公式[2]进行计算:
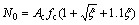 (20)
(20)
式中:N0为单肢钢管混凝土短柱极限承载力;Ac为单肢钢管混凝土核心混凝土面积;fc为单肢钢管混凝土核心混凝土强度;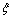 为单肢钢管混凝土套箍系数。
为单肢钢管混凝土套箍系数。
4.3 有初弯曲的轴压杆件极限荷载数值算法的实现
(1) 将压杆分为若干段(如图3)所示,各段长度可以不同,并确定各段两端和中点的坐标。
(2) 将各柱肢截面划分为若干个面积单元(如图2所示),确定各划分单元的面积Ai和中点坐标yi。
(3) 给定轴压力P。
(4) 假定由P力产生的杆端A点的转角θA即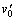 ,从杆端A开始向杆端B依次逐段计算。
,从杆端A开始向杆端B依次逐段计算。
(5) 假定第1段中点曲率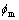 和截面形心处的平均应变ε0。
和截面形心处的平均应变ε0。
(6) 按式(10)和(13)计算每段中截面上的柱肢各划分单元应变。
(7) 按式(9)和(12)计算压杆柱肢每段中截面的合抵抗力。
(8) 校合压杆每段中截面内外轴力平衡条件,即是否满足式(14),若不满足规定的精度要求,则调整ε0,重复步骤(6)~(8)的计算直到满足要求为止。
(9) 按式(19)计算压杆每段中点位移。
(10) 按式(16)检算压杆每段中截面内外力矩平衡条件,若不满足规定的精度要求,则调整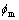 ,重复步骤(6)~(10)的计算直到满足为止。
,重复步骤(6)~(10)的计算直到满足为止。
(11) 按式(17)和(18)计算压杆每段终点的位移和斜率。
(12) 进入下一段的计算,可以用前一段已计算得到的曲率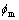 和平均应变ε0作为假定值,重复步骤(6)~(12)的计算,直到最后一段。
和平均应变ε0作为假定值,重复步骤(6)~(12)的计算,直到最后一段。
(13) 校核杆端B点的边界条件是否满足,即v=vB,若不满足规定的精度要求,则调整θA,重复步骤(3)~(13)的计算,直到满足精度要求为止。
(14) 按式(20)判断单肢是否达到极限承载能力,如有单肢短柱试验值,则以试验值为准。若单肢达到极限承载能力则退出循环,若未达到则增加荷载P,重复步骤(4)~(13)步的计算,便可逐步确定荷载-位移曲线。若步骤(13)不能完成,即出现发散现象,说明压弯杆件已达到或接近极限承载能力,开始进入不稳定状况。由文献[15]知:刚出现发散现象时的荷载则为极限荷载的近似值。当需要计算荷载—位移曲线的下降段时,可在求出极限荷载后,减小荷载P,调整θA和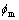 ,重复步骤(6)~(13)的计算来取得。
,重复步骤(6)~(13)的计算来取得。
5 长细比折减系数计算公式的推导
四肢缀条钢管混凝土格构柱换算长细比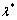 公式可参考文献[2],并作适当的调整后,如下式所示:
公式可参考文献[2],并作适当的调整后,如下式所示:
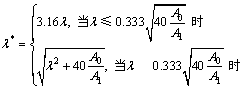 (21)
(21)
式中: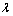 为四肢缀条钢管混凝土格构柱长细比;A0为格构柱各柱肢横截面换算面积之和;A1为格构柱横截面所截平面内各斜缀条毛截面积之和。
为四肢缀条钢管混凝土格构柱长细比;A0为格构柱各柱肢横截面换算面积之和;A1为格构柱横截面所截平面内各斜缀条毛截面积之和。
将文献[16]中钢结构相对长细比计算公式进行适当调整后,可得到考虑剪切变形及紧箍效应的四肢缀条钢管混凝土格构相对长细比计算公式如下:
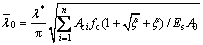 (22)
(22)
式中: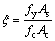 ;Aci及Ac为格构柱各柱肢核心混凝土面积;fc为格构柱柱肢核心混凝土强度;As为格构柱柱肢钢管面积;Es为格构柱柱肢钢管弹性模量;n为柱肢数。
;Aci及Ac为格构柱各柱肢核心混凝土面积;fc为格构柱柱肢核心混凝土强度;As为格构柱柱肢钢管面积;Es为格构柱柱肢钢管弹性模量;n为柱肢数。
考虑钢材强度及混凝土强度对四肢缀条钢管混凝土格构柱相对长细比折减系数的影响,将四肢缀条钢管混凝土格构柱相对长细比作适当调整后,如下式 所示:
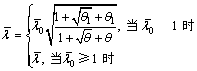 (23)
(23)
参考文献[16]中钢结构相对长细比折减系数公式,并将钢结构的长细比换成考虑剪切变形及紧箍效应的四肢缀条钢管混凝土格构柱相对长细比后,可得四肢缀条钢管混凝土格构柱相对长细比折减系数公式如下:
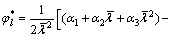
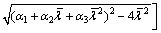 (24)
(24)
式中: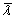 为格构柱相对长细比;
为格构柱相对长细比;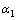 ,
,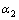 和
和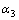 为待定系数;
为待定系数;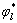 为长细比折减系数。
为长细比折减系数。
将四肢缀条钢管混凝土格构柱压杆中截面初始挠度考虑成压杆长度的1/1 000,利用本文数值计算方法对不同形式轴压杆件进行了大量数值计算。同时以式(24)作为相对长细比折减系数计算公式原型,利用数值计算结果对其系数进行拟合后,得出相对长细比折减系数半经验半理论公式如下:

将上式化简后得:
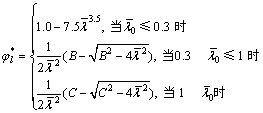 (25)
(25)
式中: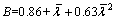 ;
;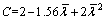 。
。
利用式(25)可得轴压四肢缀条钢管混凝土格构柱的极限承载力为:
 (26)
(26)
式中: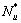 为极限承载力;
为极限承载力;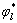 为格构柱相对长细比折减系数,由式(25)确定;N0i为格构柱单肢短柱极限承载力,由式(20)确定,若有单肢短柱极限承载力试验值,以试验值为准。
为格构柱相对长细比折减系数,由式(25)确定;N0i为格构柱单肢短柱极限承载力,由式(20)确定,若有单肢短柱极限承载力试验值,以试验值为准。
6 计算方法及计算公式的验证
利用上述数值计算方法对文献[14]中的6个缀条同向布置的轴压四肢钢管混凝土格构柱试件和本文所做的5个缀条反向布置的轴压四肢缀条钢管混凝土格构柱试件在取压杆中截面初始挠度为压杆长度的 1/1 000时的极限承载力进行计算,并与常用规程[4]的计算结果进行比较。其中本文所做试件的参数与构造见表1和图4;数值计算结果、规范计算结果、公式(26)计算结果及试验结果的比较见表2。
从表2可以看出:常用规程[4]的计算结果与本文数值计算结果及试验结果均有一定偏差;本文数值计算结果与试验结果较吻合,偏差平均值为0.999,方差为0.000 1,验证了本文数值计算方法的正确性及稳定性;本文中(26)计算结果与数值计算结果及试验结果较吻合,其与试验结果偏差平均值为0.983,方差为0.000 4,从而验证了本文计算式(26)的正确性及稳定性。
表1 试件参数
Table 1 Parameters of specimens
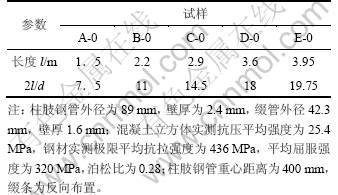
表2 计算结果比较
Table 2 Comparisons of results
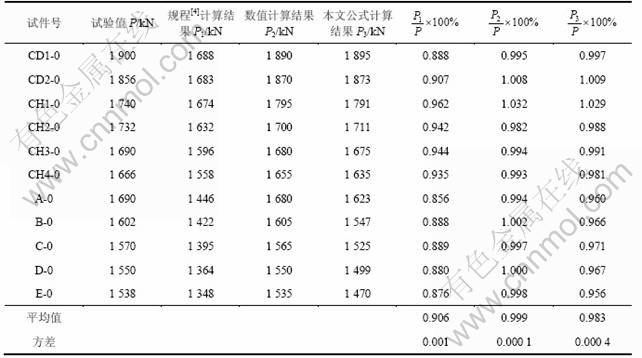
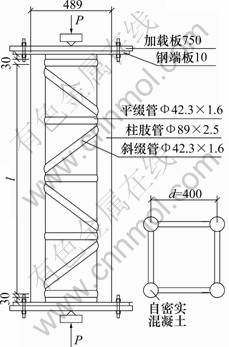
图4 试件构造图(单位:mm)
Fig.4 Configuration of specimens
7 结论
(1) 当取半正弦波初弯曲挠度为构件长度的 1/1 000时,数值计算结果与试验结果吻合良好, 偏差平均值为0.999,方差为0.000 1,验证了本文数值计算方法的正确性,同时也说明取初始挠度为构件长度 1/1 000的半正弦波模拟构件初始缺陷是合理的。
(2) 本文计算公式与试验结果较吻合,偏差平均值为0.983,方差为0.000 4,可用于规程的修订参考。
参考文献:
[1] 陈宝春, 陈友杰, 王来永, 等. 钢管混凝土偏心受压应力-应变关系模型研究[J]. 中国公路学报, 2004, 17(1): 23-28.
CHEN Bao-chun, CHEN You-jie, WANG Lai-yong, et al. Stadu of stress-strain relation of concrete filled steel tubular eccentric compression solumn[J]. China Journal of Highway and Transport, 2004, 17(1): 23-28.
[2] 蔡绍怀. 现代钢管混凝土结构[M]. 修订版. 北京: 人民交通出版社, 2007: 1-42.
CAI Shao-huai. Modern steel tube confined concrete structures[M]. Rev Ed. Beijing: China Communication Press, 2007: 1-42.
[3] 韩林海. 管混凝土结构[M]. 北京: 科学出版社, 2007: 1-35.
HAN Lin-hai. Concrete filled steel tube structure[M]. Beijing: Science Press, 2007: 1-35.
[4] CECS 28:90. 钢管混凝土结构设计与施工规程[S].
CECS 28:90. Concrete filled steel tube structure design and construction code[S].
[5] DL/T 5085—1999. 钢管混凝土组合结构设计规程[S].
DL/T 5085—1999. Concrete filled steel tube composite structure design code[S].
[6] JCJ 01—89. 钢管混凝土结构设计与施工规程[S].
JCJ 01—89. Concrete filled steel tube structure design and construction rules[S].
[7] 邓玉孙, 熊刚, 聂诗东. 双肢缀条格构柱换算长细比的补充[J]. 工业建筑, 2006, 36(增刊): 445-447.
DENG Yu-sun, XIONG Gang, NIE Shi-dong. Supplement to modified column slenderness ratio of built-up member with tie plates[J]. Industrial Construction, 2006, 36(Supple): 445-447.
[8] 蒋丽忠, 周旺保. 一种钢管混凝土格构柱极限承载力的快速计算方法[J]. 计算力学学报, 2010, 27(4): 1-5.
JIANG Li-zhong, ZHOU Wang-bao. A high-speed calculating method of the bearing capacity of the latticed column of concrete filled steel tube[J]. Chinese Journal of Computational Mechanics, 2010, 27(4): 1-5.
[9] 蒋丽忠, 周旺保, 伍振宇, 等. 四肢钢管混凝土格构柱极限承载力的试验研究与理论分析[J]. 土木工程学报, 2010, 43(9): 1-8.
JIANG Li-zhong, ZHOU Wang-bao, WU Zhen-yu, et al. Experimental study and theoretical analysis on the ultimate load carrying capacity of four-tube concrete filled steel tubular lattice columns[J]. China Civil Engineering Journal, 2010, 43(9): 1-8.
[10] 蒋丽忠, 周旺保, 唐斌. 钢管混凝土格构柱偏压承载力分析的数值方法[J]. 计算力学学报, 2010, 27(1): 127-131.
JIANG Li-zhong, ZHOU Wang-bao, TANG Bin. The numerical analysis method of the eccentric compression bearing capacity for the concrete filled steel tubular latticed columns[J]. Chinese Journal of Computational Mechanics, 2010, 27(1): 127-131.
[11] Kil P A E, Vija Y R B. Tests on high-strength concrete-filled steel tubular columns[J]. ACI Structural Journal, 1999, 96(2): 268-274.
[12] GB 50017—2003. 钢结构设计规范[S].
GB 50017—2003. Steel structure design code[S].
[13] 陈宝春, 欧智菁. 钢管混凝土格构柱极限承载力计算方法研究[J]. 土木工程学报, 2008, 41(1): 55-63.
CHEN Bao-chun, OU Zhi-jing. Calculation method for the ltimate load carrying capacity of concrete-filled steel tubular lattice columns[J]. China Civil Engineering Journal, 2008,41(1): 55-63.
[14] 陈宝春, 欧智菁. 四肢钢管混凝土格构柱极限承载力试验研究[J]. 土木工程学报, 2007, 40(6): 32-41.
CHEN Bao-chun, OU Zhi-jing. Experimental study on the ultimate load carrying capacity of four-tube concrete filled steel tubular laced columns[J]. China Civil Engineering Journal, 2007, 40(6): 32-40.
[15] 夏志斌, 潘有昌. 结构稳定理论[M]. 北京: 高等教育出版社, 1987: 160-168.
XIA Zhi-bin, PAN You-chang. Structural stability theory[M]. Beijing: Higher Education Press, 1987: 160-168.
[16] 沈祖炎, 陈扬骥, 陈以一. 钢结构基本原理[M]. 北京: 中国建筑工业出版社, 2005: 101-110.
SHEN Zu-yan, CHEN Yang-yi, CHEN Yi-yi. Steel structure basic principle[M]. Beijing: China Architecture & Building Press, 2005: 101-110.
[17] 陈宝春, 欧智菁. 钢管混凝土偏压格构柱长细比影响试验研究[J]. 建筑结构学报, 2006, 27(4): 72-79.
CHEN Bao-chun, OU Zhi-jing. Experimental study on influence of slenderness ratio in concrete filled steel tubular laced columns under eccentric compression[J]. Journal of Building Structures, 2006, 27(4): 72-79.
[18] 刘晶波, 杜修力. 结构动力学[M]. 北京: 机械工业出版社, 2006: 157-158.
LIU Jin-bo, DU Xiu-li. Structural dynamics[M]. Beijing: China Machine Press, 2006: 157-158.
(编辑 赵俊)
收稿日期:2010-08-20;修回日期:2010-11-02
基金项目:国家自然科学基金资助项目(50778177);湖南省杰出青年基金资助项目(07JJ1009)
通信作者:周旺保(1982-),男,湖南岳阳人,博士研究生,从事组合结构和工程抗震研究;电话:15116335688;E-mail: zhouwangbao@163.com