J. Cent. South Univ. (2017) 24: 1594-1601

DOI: 10.1007/s11771-017-3564-z

System structural analysis of communication networks based on DEMATEL-ISM and entropy

FU Kai(付凯)¹, XIA Jing-bo(夏靖波)², ZHANG Xiao-yan(张晓燕)¹, SHEN Jian(申健)¹

1. Information and Navigation College, Air Force Engineering University, Xi’an 710077, China;

Central South University Press and Springer-Verlag Berlin Heidelberg 2017

Abstract: A method of system structural analysis based on decision making trial and evaluation laboratory together with interpretative structural modeling (DEMATEL-ISM) and entropy is proposed to clarify system structure of communication networks and analyze mutual influencing degree between different networks. Mutual influencing degree and importance degree of elements are both considered to determine weights of elements, and the entropy of expert judgment results is used to omit unimportant influence relation and simplify system structure. Structural analysis on communication networks system shows that the proposed method can quantificationally present weights and mutual influencing degree of elements, and reasonably simplify system structure. The results indicate the rationality and feasibility of the method.

Key words: communication networks; system structural analysis; decision making trial and evaluation laboratory (DEMATEL); interpretative structural modeling (ISM); entropy

1 Introduction

With the development of information technologies such as information grid [1], cloud computing, and network virtualization [2], communication networks progress in extensive interconnection by multi-means and mixing of multi-networks, and its functions change from traditional message transmission to intelligent information service [3]. With the progress of network construction, communication networks turn into a complex system, which brings great challenges to management and performance evaluation of networks. It is important to clarify system structure of communication networks and analyze mutual influencing degree between different networks for realizing intelligent network management.

Methods such as decision making trial and evaluation laboratory (DEMATEL) [4], interpretative structural modeling (ISM) [5], analytic hierarchy and network processes (AHP/ANP) [6, 7] have been widely used in domain of system structural analysis. DEMATEL method clarifies contribution degree and relation degree of elements in system, ISM method realizes grade division of system structure, and ANP method adds mutual influence relation of elements based on AHP method. Many researchers proposed integrating methods to overcome the weakness of applying one of these methods alone as they are complementary in function. As a new way of system structural analysis, DEMATEL-ISM [8, 9] method integrates two methods to analyze system structure by converting the total influence matrix to the reachability matrix, but it ignores mutual influencing degree between elements. ZHANG et al [10] researched structural model of key factors in enterprise management information system of manufacturing industries, which obtained the reachability matrix with improved Boolean algebra algorithms and realized quantification of mutual influencing degree between elements and grade division of system structure. LI et al [11, 12] proposed a new system structural analysis arithmetic with reachable effect factor based on DEMATEL-ISM, which effectively implemented the system structure analysis based on the fact that unimportant elements and their influence relations were omitted, and that they realized the quantification of mutual influencing degree between important elements, but it was possible to lead to a wrong grade division of isolated elements after omitting elements. Since DEMATEL method neglected the distinction of weights of elements, DEMATEL-ANP method [13, 14] introduced comprehensive weights of elements, but it was complicated for implementing expert judgment of influence relation and importance degree of elements. YUAN et al [15] integrated three kinds of method including DEMATEL, ISM and ANP to analyze vulnerability factors for urban rail transit system.

In this work, a method of system structural analysis based on DEMATEL-ISM and entropy is proposed, aimed at solving problems in above methods. Basic principle of the proposed method is elaborated at first, the implementation process is given then, and example analysis of communication networks testifies the rationality and superiority of the method finally.

2 Method of system structural analysis

2.1 Basic principle

The proposed method implemented system structural analysis in consideration of mutual influencing degree between elements, importance degree of elements and effect of grade division, and it quantificationally analyzed weights and mutual influencing degree between elements. In the process of analyzing influence relation between elements, comprehensive judgment grade was designed, considering mutual influencing degree and importance degree of elements to obtain weighted influence matrix, which reduced times of expert judgment and avoided the problem that important degree of elements was neglected. In the process of grade division, mutual influencing degree between elements and the entropy of expert judgment results were both considered to omit unimportant influence relation, which increased the certain degree in omitting influence relation. At last, system structure repair was made for isolated elements generated by omitting influence relation in order to simplify but not destroy system structure.

2.2 Implementation process

Step 1: Analyze elements of system

Let n elements of system be E_i (i=1, 2, …, n).

Step 2: Calculate the weighted direct influence matrix A according to expert judgment results

Some experts are asked to rate the direct influence that element E_i has on element E_j and the relative importance degree between element E_i and element E_j using an integer scale ranging from 0 to 10 as shown in Table 1. The judgment degree of element E_i to element E_j is big if element E_i has great direct influence on element E_j, and element E_i is more important than element E_j. Then the weighted direct influence matrix A is calculated according to the average value of judgment results of m experts. The matrix A represents mutual influencing degree and relative importance degree between elements, so it can be regarded as a weighted influence matrix.

Table 1 Comprehensive judgment grade

Step 3: Calculate the normalized direct influence matrix N

The normalized direct influence matrix N can be obtained by normalizing the weighted direct influence matrix A as

                           (1)

Step 4: Calculate the weighted total influence matrix T

In original DEMATEL method, experts just rate the mutual influencing degree between elements, and the total influence matrix calculated by the direct influence matrix represents direct and indirect influencing degree between elements. In the proposed method of this work, grades 1-3 in the weighted direct influence matrix just represent relative importance degree rather than mutual influencing degree between elements. So, when indirect influencing degree is calculated the additional influence generated by transmission of relative importance degree should be omitted, and elements in the weighted total influence matrix should be calculated according to the grades of elements in the weighted direct influence matrix as follows. For influence relations in grades 1-3 that represent no direct influence between elements, the total influencing degree is calculated by relative importance degree plus the possible indirect influencing degree. For influence relations in grades 4-9 that represent little or great direct influence between elements, the total influencing degree is calculated by weighted direct influencing degree plus weighted indirect influencing degree. The matrix T can be calculated as

                        (2)

     (3)

                     (4)

where I is the unit matrix, and

Step 5: Calculate weights of elements

Let the row sum P_i of the total relation matrix T be the degree of influence of element E_i and the column sum Q_i be the degree of being influenced of element E_i. W_i is defined as the weight of element E_i by calculating the normalized value of the quotient of P_i and Q_i, and it can be calculated as

                                  (5)

                                  (6)

                                 (7)

                              (8)

The weight of element represents importance degree of element and its influence on other elements, and it is big if the element is more important than other elements and has great influence on other elements. The degree of influence and degree of being influenced in this work are weighted influencing degree, so it is reasonable to calculate weights by the quotient of them.

Step 6: Calculate the entropy matrix S

In order to simplify system structure, unimportant influence relation between elements should be omitted. Because expert judgment results are seriously affected by personal experience and subjective factors, and only unanimous judgment results can be highly trusted. The entropy [16] is used to describe the certain degree of judgment results in this work, and only very certain and little influence relation in grades 4-6 can be omitted, thus reducing the risk of omitting important influence relation caused by subjective judgment of experts.

Let expert judgment results of E_i to E_j be to and The value of can be regarded as disperse probability distribution of m results, and the entropy of expert judgment results is calculated only for little influence relations in grades 4-6. The entropy matrix S of expert judgment results is defined as [17]

(9)

Step 7: Calculate the weighted holistic influence matrix H and weighted reachability matrix R

The matrix T^* obtained in the process of getting matrix T is calculated after omitting element relation of no direct influence, so it represents the sum of direct and indirect influencing degree between elements. Added with the influence on the element itself, the weighted holistic influence matrix H is obtained as

                                (10)

In order to simplify system structure, the weighted reachability matrix R can be obtained from matrix H by omitting unimportant influence relation according to the classification as follows. Influence relations in grades 1-3 which contain neither direct influence nor indirect influence is omitted. Influence relations in grades 1-3 which contain indirect influence rather than direct influence is omitted if its total influence value of matrix T_ij is smaller than the threshold, T_m. Influence relations in grades 4-6 which contain little direct influence is omitted if its entropy is greater than the threshold, S_m. Influence relations in grades 7-9 which contains great direct influence is not omitted. The weighted reachability matrix R obtained after omitting influence relations can present mutual influencing degree between elements quantificationally, and the value of matrix R_ij calculated as Eq. (11) is just mutual influencing degree between element E_i and element E_j.

              (11)

Step 8: Implement domain decomposition for matrix H

The matrix H represents holistic influence relation of elements, so implementing domain decomposition for matrix H can avoid the mistake in domain decomposition after omitting relation. For element E_i, calculate the reachable setand the antecedent set n} according to the matrix H. Let If E_p and are two disparate elements in set and E_p, E_q and elements in and are in the same domain, otherwise they are in different domains.

Step 9: Implement grade division for matrix R

The matrix R only represents important influence relation of elements, so implementing grade division for matrix R can simplify system structure. For element E_i, calculate the reachable set and the antecedent set according to the matrix R. Let For elements in the same domain, take elements in set E(E_i) as the highest grade. Then, omit the elements ranked, and obtain elements in the lower grade in the same way till all elements in the system are ranked.

After omitting influence relation between elements, some isolated elements in low grade are likely to be put into the highest grade. So, original system structure is destroyed, and system structure repair is necessary. If the influencing degree value between element E_p and other elements is zero after omitting influence relation and E_p has direct influence on at least one element E_q in the present grade (A_pq>3), put element E_p into the adjacent lower grade. Repeat it till above conditions are not satisfied or element E_p is in the lowest grade.

Step 10: Draw the system structure chart

Draw the system structure chart which quantificationally presents weights and mutual influencing degree of elements.

According to above steps, implementation flow of the proposed method of system structural analysis based on DEMATEL-ISM and entropy is shown in Fig. 1.

Fig. 1 Implementation flow of proposed method

2.3 Parameters setting

Parameter T_m and S_m are related to the quantity of omitted relation. Parameters setting should omit influence relation to simplify system structure and not destroy the system structure meanwhile.

Parameter T_m is used to omit little influence relation according to the total influencing degree between elements, and relative value of total influencing degree is related to all the value of that, so T_m is defined as

          (12)

where is the nonzero value of total influencing degree of element E_i to element E_j, and 0<λ<1, let λ=1/3 in this work.

Parameter S_m is used to omit unimportant influence relation according to the entropy of expert judgment results. S_m is set in the range of 0.9-1 generally, and it is set according to the ratio of omitting influence relation R_o defined as Eq. (13) and the ratio of losing influence value R_l defined as Eq. (14) in this work. R_o represents the degree of omitting influence relation, and R_l represents the degree of destroying system structure. Parameters should be set to increase value of R_o and decrease value of R_l, namely increasing the value of R_o/R_l.

                                 (13)

                                  (14)

where Q_om is the quantity of omitted influence relation, Q_or is the quantity of original influence relation before omitting influence relation, V_om is the sum of omitted total influence value, and V_or is the sum of original total influence value before omitting influence relation.

3 System structural analysis of communication networks

Communication networks researched in this work contain ten kinds of network including fiber network, satellite network, data communication network, telephone network and so on, and wired and wireless communication means are used to provide many kinds of communication service such as voice, data and video. Various influence relation exists among networks, and all networks jointly constitute the complex system of communication networks. In order to clarify system structure of the communication networks and analyze mutual influencing degree between networks, the proposed method in this work is applied. Let each network in the communication networks system be the element E_i (i=1, 2, …, 10), and five experts familiar with communication networks are asked to judge the influence relation between networks. Then, the weighted direct influence matrix A and the weighted total influence matrix T are calculated.

The degree of influence, P_i, the degree of being influenced, Q_i, and the weight, W_i, of networks are calculated as shown in Table 2, and the influence relation of networks is visually shown in Fig. 2. The horizontal coordinate of each point in Fig. 2 represents the degree of being influenced while the vertical coordinate of each point represents the degree of influence, and the slope of the line connected by each point and the original point represents the weight of each network.

Table 2 Calculated parameters of networks

Parameters T_m and S_m need to be set reasonably in order to omit unimportant influence relation. According to the matrix T^*, the quantity of original relation is 23, and the sum of original total influence value is 2.19. Let T_m=0.06 by using Eq. (12), and results of R_o and R_l in different cases where values of S_m varies from 0.9 to 1 are shown in Table 3.

As is shown in Table 3, the value of R_o/R_l both achieves the maximum when S_m is 0.92, 0.93 and 0.94, and the value of R_o and R_l are in acceptable range meanwhile. Parameter S_m is expected to be big because it can increase the certain degree in omitting influence relation, so let S_m=0.94.

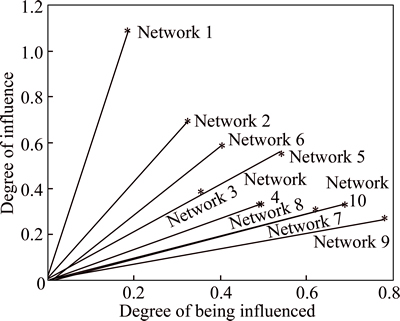
Fig. 2 Influence relation of networks

Table 3 Parameter setting for S_m

After parameters setting, the weighted reachability matrix R is calculated by the weighted holistic influence matrix H.

Implement domain decomposition for matrix H, and all elements are proved to be in the same domain. Implement grade division for matrix R, and the process is shown in Table 4.

Table 4 Process of grade division

After preliminary grade division, networks 3 and 4 in grade 1 are isolated elements which have direct influence on some elements in grades 1 and 2 (values of A₃₅, A₃₇, A₄₅ and A₄₇ are all greater than 3), so network 3 and 4 are put into grade 3 through system structure repair. Final result of grade division is that the system is divided into three grades, namely grade 1 including elements E₇, E₈, E₉ and E₁₀, grade 2 including elements E₅ and E₆, grade 3 including elements E₁, E₂, E₃ and E₄. System structure of communication networks is shown in Fig. 3, which can quantificationally present weights and mutual influencing degree of networks.

As is shown in Fig. 3, networks 1 and 2 with big weight are extremely important in communication networks system, and should be paid more attention to in daily network management. Network 1 has homogeneous influence on the four carrying networks including networks 5-8, but network 2 has greater influence on network 9 than that on networks 5 and 6. So, if there is something wrong with network 2, its’ influence on other networks are different. Networks 3 and 4 have little influence on other networks, so influence relation of the two networks are omitted. Networks 5 and 6 have influence on others and are influenced by others, while networks 7-10 are only influenced by others. Above analysis can help to obtain systemic understanding on system structure and influence relation of communication networks, and provide valuable reference for network construction and management.

Compared with other methods, the proposed method in this work takes mutual influencing degree and importance degree of elements into account. Meanwhile it simplify system structure by omitting unimportant influence relation has good effect of grade division. Comparison of methods is shown in Table 5.

4 Conclusions

1) A method of system structural analysis based on DEMATEL-ISM and entropy is proposed and applied to communication networks, which is significant for performance evaluation and fault diagnosis of communication networks. Example analysis indicates that the proposed method can clarify system structure of communication networks and quantificationally analyze mutual influencing degree between different networks, and has advantages in evaluating weights of networks and grade division.

2) Expert judgment is implemented once and the entropy of expert judgment results is used to omit unimportant influence relation in the proposed method, but the problem that expert judgment is seriously affected by subjective factors and difficult to be implemented is inevitable. Methods such as neural network [18] will be considered in future research.

Fig. 3 System structure of communication networks

Table 5 Comparison of methods

References

[1] HUNG B, DEFRANCESCO D, CHENG B N, SUKUMAR P. An evaluation of IP header compression on the GIG joint IP modem system [C]// Proceedings of 2014 IEEE Military Communications Conference. Baltimore, USA: IEEE, 2014: 1484-1490.

[2] CHOWDHURY N M K, BOUTABA R. A survey of network virtualization [J]. Computer Networks, 2010, 54(5): 862-876.

[3] WU Qing-hua, LI Zhen-yu, Zhou Jian-er, JIANG Heng, HU Zhi-yang, LIU Yun-jie, XIE Gao-gang. SOFIA: Toward service- oriented information centric networking [J]. IEEE Network, 2014, 28(3): 12-18.

[4] TSENG M L. Using the extension of DEMATEL to integrate hotel service quality perceptions into a cause-effect model in uncertainty [J]. Expert Systems with Applications, 2009, 36(5): 9015-9023.

[5] LIANG Ying. Online experiment mode of computer basic courses based on ISM method [C]// Proceedings of the 6th International Conference on Computer Science & Education (ICCSE 2011), SuperStar Virgo, Singapore: ICCSE, 2011: 974-977.

[6] SAATY T L. Decision making-the analytic hierarchy and network processes (AHP/ANP) [J]. Journal of Systems Science And Systems Engineering, 2004, 13(1): 1-35.

[7] JAYAKRISHNA K, VIMAL K E K, SEKAR V. ANP based sustainable concept selection [J]. Journal of Modelling in Management, 2015, 10(1): 118-136.

[8] ZHOU De-qun, ZHANG Ling. Establishing hierarchy structure in complex systems based on the integration of DEMATEL and ISM [J]. Journal of Management Sciences in China, 2008, 11(2): 20-26. (in Chinese)

[9] SHEN Gui-xiang，SUN Shu-guang，ZHANG Ying-zhi，WANG Zhi-qiong, CHEN Bing-kun, MA Chuang. System failure analysis based on DEMATEL-ISM and FMECA [J]. Journal of Central South University, 2014, 21(12): 4518-4525.

[10] ZHANG Xiang-bin, JIANG Yan-li, XU Chang. Analysis of factors influencing implementing enterprise management information System (ERP) in the manufacturing industries [J]. Information Science, 2006, 24(12): 1866-1869. (in Chinese)

[11] LI Ming-hui, XIA Jing-bo, CHEN Cai-qiang. Network pedigree model with reachable effect factor base on DEMATEL & ISM [J]. Journal of Jilin University: Engineering and Technology Edition, 2012, 42(3): 782-788. (in Chinese)

[12] LI Ming-hui, XIA Jing-bo, CHEN Cai-qiang, YIN Bo, WANG Kai. A new system structure analysis arithmetic with reachable effect factor [J]. Transaction of Beijing Institute of Technology, 2012, 32(2): 135-140. (in Chinese)

[13] HUANG C N, LIOU J J H, CHUANG Y C. A method for exploring the interdependencies and importance of critical infrastructures [J]. Knowledge-Based Systems, 2014, 55: 66-74.

[14] HSU C C, LIOU J J H, CHUANG Y C. Integrating DANP and modified grey relation theory for the selection of an outsourcing provider [J]. Expert Systems with Applications, 2013, 40(6): 2297-2304.

[15] YUAN Peng-wei，SONG Shou-xin，DONG Xiao-qing, LIN Xiao-fei. Vulnerability identification model of urban rail transit system [J]. Journal of Transportation Systems Engineering and Information Technology, 2014, 14(5): 110-118. (in Chinese)

[16] BATTY M, MORPHET R, MASUCCI P, MASUCCI P. Entropy, complexity, and spatial information [J]. Journal of Geographical Systems, 2014, 16(4): 363-385.

[17] ZHU Chun-yan, YANG Ming-shun, GAO Xin-qin, YANG Xu-chang. Modifying the importance ratings of customer requirements based on DEMATEL and entropy [J]. Industrial Engineering and Management, 2012, 17(3): 97-101. (in Chinese)

[18] QIN Xiao-nan, LU Xiao-li. A BP-DEMATEL-Model-based research of the factors that affect coastal urban ecological security system [J]. Management Review, 2015, 27(5): 48-57. (in Chinese)

(Edited by DENG Lü-xiang)

Cite this article as: FU Kai, XIA Jing-bo, ZHANG Xiao-yan, SHEN Jian. System structural analysis of communication networks based on DEMATEL-ISM and entropy [J]. Journal of Central South University, 2017, 24(7): 1594-1601. DOI: 10.1007/s11771-017-3564-z.

Foundation item: Project(20141996018) supported by Aerospace Science Foundation of China; Project(2012JZ8005) supported by the Natural Science Fundamental Research Planned Project of Shanxi Province, China

Received date: 2015-12-16; Accepted date: 2016-08-01

Corresponding author: FU Kai, PhD Candidate; Tel: +86-18176262801; E-mail: fukaia3@163.com