DOI: 10.11817/j.issn.1672-7207.2015.09.046
火电单元机组机炉协调柔性自抗扰控制
董君伊,孙立,李东海
(清华大学 热能工程系,电力系统国家重点实验室,北京,100084)
摘要:针对火电单元机组机炉协调系统中普遍存在的强耦合、参数时变、大范围变工况运行等问题设计柔性自抗扰控制方案。首先,利用柔性控制结构调整系统接近能量供需平衡,解决系统输出在快速性和稳定性之间的矛盾。在此基础上,设计自抗扰控制器对系统中的扰动、不确定性等进行估计和补偿,使控制系统具有较强的抗干扰能力和对机组变工况运行的自适应能力。根据实际控制要求,进行设定值跟踪实验、输入扰动实验、变工况实验和蒙特卡罗实验。研究结果表明:所设计方案综合柔性控制结构和自抗扰控制器的优点,具有良好的控制品质和很强的性能鲁棒性。
关键词:火电单元机组机炉;柔性控制;自抗扰控制;蒙特卡罗实验;鲁棒性
中图分类号:TK323 文献标志码:A 文章编号:1672-7207(2015)09-3503-10
Flexible active disturbance rejection control for boiler–turbine unit
DONG Junyi, SUN LI, LI Donghai
(State Key Laboratory of Power Systems, Department of Thermal Engineering, Tsinghua University,
Beijing 100084, China)
Abstract: Considering that the boiler–turbine unit, which has strong coupling, large inertia and parameter uncertainties, is a critical part to the modern power plant, a novel flexible active disturbance rejection control scheme for a boiler-turbine system was presented. Firstly, a flexible structure was utilized to achieve the energy feed-demand balance, which can improve the dispatch rate while keep the steam pressure stable at the same time. Secondly, the active disturbance rejection controller was applied to estimate and actively compensate the disturbances, the parameter uncertainties as well as the unmodeled dynamics in the system. Simulations were conducted under different operating conditions. The results show that the proposed control scheme illustrates the advantages of flexible structure and active disturbance rejection controller, and has excellent performance and strong robustness.
Key words: boiler–turbine unit; flexible control; active disturbance rejection controller; Monte Carlo experiment; robustness
火电单元机组机炉协调系统是一个复杂的多变量系统,具有大惯性、强耦合、参数时变等特点,对其有效控制对实现电网的自动调度意义重大。机炉协调控制的主要目标是满足电网对负荷的需求,同时维持机组运行参数稳定[1]。然而,锅炉和汽机在能量转换过程中的速度相差较大,导致系统输出在快速性和稳定性之间存在固有矛盾,因此,机炉协调控制一直是单元机组控制中的难题。目前,国内外很多学者对机炉协调控制进行了研究。在这些研究中,虽然使用的控制算法各异,但控制方案的设计大致分为2类:第1类方案对模型进行线性化处理并设计线性控制器。Hamed等[2]在模型反馈线性化的基础上设计PI控制器;Chen等[3]将非线性的机炉协调系统转换为一个变参数的线性系统,设计状态反馈控制器;Jalali等[4]采用多模型控制,基于局部线性化模型设计一族PI控制器。第2类方案采用非线性控制器处理机炉协调系统中的非线性环节。Fang等[5]基于反演法设计非线性自适应控制器;Yang等[6]首先设计1个有限时间收敛的控制器使状态变量收敛到各自的设定值,然后针对系统中的非线性和不确定性设计自适应控制器;Li等[1, 7-8]建立TS模糊模型来逼近机炉协调系统的动态特性,分别设计基于遗传算法的模型预测控制器、基于迭代学习的模型预测控制器以及H∞非线性状态反馈跟踪控制器。上述控制方案虽然改善了机炉协调系统的控制品质,但都不可避免地存在一些弊端,如依赖对象精确模型、控制结构复杂、计算量大、计算时间长等[9],这些缺点限制了上述控制方案的工程应用。单元机组的本质是实现物质以及能量的转换。于达仁等[10]从能量供需的角度分析了机炉协调系统的动态特性,指出能量供应不足导致主汽压力波动过大,能量供应缓慢导致负荷适应性较差,并提出可以通过柔性结构调整系统实现能量供需的平衡。本文在柔性结构的框架下,为机炉协调系统设计自抗扰控制器(active disturbance rejection controller, ADRC),以提高控制系统的抗干扰能力、鲁棒性以及对机组变工况运行的自适应能力。自抗扰控制器具有结构简单、不依赖于对象精确模型、鲁棒性强等特点。ADRC的核心是将被控对象中的非线性、干扰、不确定性等看作扩张状态进行估计,估计量由控制率来补偿[11]。赵志良[12]证明了ADRC在扩张状态有界时的收敛性,Yang等[13]给出了ADRC可以估计的扰动范围。为了便于ADRC的工程应用,Gao[14]将ADRC简化为线性形式并提出了基于带宽的参数整定方法,使ADRC的参数整定环节简单易行。目前,ADRC已被用于控制永磁同步电机[15]、热连轧板宽板厚[16]等,取得了良好的控制效果,显示了ADRC在实际应用中的发展前景。本文作者以某300 MW燃煤直流炉再热机组在100%负荷工作点处的线性化模型为被控对象,设计柔性自抗扰控制方案。首先,以时间乘以误差绝对值积分指标作为评价标准,选取最优柔性因子,使系统接近于能量供需平衡,解决机组快速性和稳定性之间的矛盾。在此基础上,用自抗扰控制器对系统中的扰动、未建模动态等进行估计和补偿,使控制系统具有较强的抗干扰能力和鲁棒性;将基于100%工况设计的控制器用于70%工况,检验控制器对变工况运行的适应能力。
1 机炉协调系统柔性控制结构
火电单元机组的主要任务是将燃料的化学能转换为电能并输出给电网。图1所示为单元机组的示意图。图1中:uB为燃烧率;uT为汽机阀门开度;NE为机组实发电功率;PT为机前主汽压力。机炉协调控制的首要目标是在满足电网对负荷需求的同时维持主汽压力的稳定。因此,通常将协调控制系统设计为以uB和uT为输入,NE和PT为输出的系统。目前,机炉协调控制常用的策略有基于“机跟炉”的协调控制和基于“炉跟机”的协调控制。前者可维持主汽压力在运行过程中处于相对稳定状态,但负荷适应性差;后者虽可使负荷响应迅速,但主汽压力波动较大。从能量转换的角度看,锅炉侧由于包含大惯性环节,能量转换速度较汽机侧慢很多。锅炉和汽机在能量转换速度上的差异导致能量供需不平衡,使得系统输出在快速性和稳定性之间存在矛盾[10]。基于此,于达仁等[10]提出柔性控制结构,通过对不同速度的能量转换过程进行协调,寻求锅炉和汽机间的能量供需平衡。图2所示为柔性控制结构的示意图[10]。图2中:NS和 PS分别表示功率回路和压力回路的设定值。将功率信号和汽压信号以加权方式同时送入锅炉控制器和汽机控制器,各通道增益(加权系数)分别为 ,
,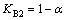 (
( 为柔性因子),
为柔性因子), ,
, ,可知:当
,可知:当 =0时,KB1=0,KB2=1,KT1=1,K T2=0,机组运行方式为基于“机跟炉”的协调控制,系统以能量供应为控制目标;当
=0时,KB1=0,KB2=1,KT1=1,K T2=0,机组运行方式为基于“机跟炉”的协调控制,系统以能量供应为控制目标;当 =1时,KB1=1,KB2=0,KT1=0,K T2=1。机组运行方式为基于“炉跟机”的协调控制,系统以能量需求为控制目标;当
=1时,KB1=1,KB2=0,KT1=0,K T2=1。机组运行方式为基于“炉跟机”的协调控制,系统以能量需求为控制目标;当 时,机组协调控制以“机跟炉”为主,控制目标更多地考虑能量供给;当
时,机组协调控制以“机跟炉”为主,控制目标更多地考虑能量供给;当 时,机组协调控制以“炉跟机”为主,控制目标更多地考虑能量需求。因此,
时,机组协调控制以“炉跟机”为主,控制目标更多地考虑能量需求。因此, 为协调能量供需的柔性因子,对
为协调能量供需的柔性因子,对 进行调整,可使机组接近能量供需平衡。处于能量供需平衡的机组,既具有较强的负荷跟踪能力,又能保证主汽压力在较小范围内波动。
进行调整,可使机组接近能量供需平衡。处于能量供需平衡的机组,既具有较强的负荷跟踪能力,又能保证主汽压力在较小范围内波动。

图1 单元机组示意图
Fig. 1 Diagram of boiler–turbine unit
2 自抗扰控制器设计
单元机组包含复杂的能量转换过程,存在很强的不确定性,且需要根据电网需求变负荷运行。在柔性结构的基础上,选用不依赖对象精确模型,鲁棒性强的ADRC作为锅炉和汽机的控制器,得到柔性自抗扰控制方案,其结构如图3所示,其中,ud1和 ud2分别模拟可能存在的锅炉侧和汽机侧的扰动。
2.1 自抗扰控制器原理
将机炉协调系统的输入简记为u1和u2,输出简记为y1和y2,考虑系统中存在未知形式的扰动ud1和 ud2, 则系统可用如下传递函数矩阵表示:

不失一般性,令
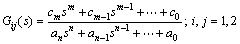
其中: ;
; ;
; ;模型参数和阶次为未知量。Gd1(s)和Gd2(s)的表达式与式(2)的类同。考虑系统的第1个回路,由式可得:
;模型参数和阶次为未知量。Gd1(s)和Gd2(s)的表达式与式(2)的类同。考虑系统的第1个回路,由式可得:

令 ,对该式进行拉普拉斯反变换得到
,对该式进行拉普拉斯反变换得到



图2 单元机组柔性控制结构示意图
Fig. 2 Diagram of flexible control for boiler-turbine unit

图3 机炉协调柔性自抗扰控制结构图
Fig. 3 Diagram of flexible ADRC for boiler-turbine unit
对于任意正整数k≥1,定义k重积分[17]:

对式中等号两端进行n-1重积分得


其中: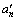 (n=1, 2, …)和
(n=1, 2, …)和 (m=1, 2, …)分别为an和cm积分后的系数。
(m=1, 2, …)分别为an和cm积分后的系数。
对式进行等价变换得



由于模型参数和阶次均为未知量,称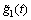 为系统内部的未知动态。同理,令
为系统内部的未知动态。同理,令 。
。 ,并分别对式(6)和(7)进行拉普拉斯反变换。在ADRC框架下,不需要知道耦合和干扰的具体时域形式,只给出其表达式:
,并分别对式(6)和(7)进行拉普拉斯反变换。在ADRC框架下,不需要知道耦合和干扰的具体时域形式,只给出其表达式:

将式简记为

由线性叠加性原理得
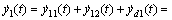

将 称为系统的扩张状态,其包含了系统内部的未知动态
称为系统的扩张状态,其包含了系统内部的未知动态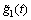 、回路间的耦合
、回路间的耦合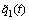 以及扰动
以及扰动 。易知扩张状态f1(t)为未知量。定义状态变量
。易知扩张状态f1(t)为未知量。定义状态变量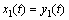 ,扩张状态变量
,扩张状态变量 ,要求
,要求 为可测量,
为可测量, 具有一阶连续导数,则式可表示为
具有一阶连续导数,则式可表示为

为了获得 的信息,Gao等[14]设计扩张状态观测器(extended state observer, ESO),其数学表达式为
的信息,Gao等[14]设计扩张状态观测器(extended state observer, ESO),其数学表达式为

其中: 和
和 为观测器参数。当ESO准确整定时,
为观测器参数。当ESO准确整定时, 和
和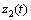 将分别跟踪
将分别跟踪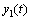 和
和 。式表示的对象设计控制率为
。式表示的对象设计控制率为

联立式和, 当ESO准确整定时,有

至此,包含未知动态、耦合、扰动的扩张状态 在被ESO估计后,由控制率进行补偿。被控对象转换为一个积分环节
在被ESO估计后,由控制率进行补偿。被控对象转换为一个积分环节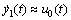 。该积分环节设计比例控制器为
。该积分环节设计比例控制器为
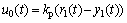
其中:r1(t)为参考输入。联立式和可得闭环微分方程:
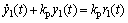
相应的闭环传递函数为

根据上述推导过程,所得ADRC的结构图见图4。同理,可为第2个回路设计自抗扰控制器。
2.2 自抗扰控制器参数整定方法
针对图4所示控制器结构,Gao[14]引入带宽的概念,将kp转换为控制器带宽 的函数,将
的函数,将 和
和 转换为观测器带宽
转换为观测器带宽 的函数,即
的函数,即
 ,
, ,
,

图4 自抗扰控制器结构
Fig. 4 Diagram of ADRC structure
至此,ADRC有3个参数需要整定,分别是 ,
, 和b0。这3个参数在实际整定过程中遵循如下规律:
和b0。这3个参数在实际整定过程中遵循如下规律:
1) 越大,ESO的观测能力越强,但这会增加观测器对噪声的敏感性。因此,
越大,ESO的观测能力越强,但这会增加观测器对噪声的敏感性。因此, 应从1个较小的值逐渐增大,直至观测精度满足要求为止。
应从1个较小的值逐渐增大,直至观测精度满足要求为止。
2) 越大,b0越小,控制作用越强,系统输出响应越快,但超调和振荡会越严重。
越大,b0越小,控制作用越强,系统输出响应越快,但超调和振荡会越严重。
在通常情况下,需根据具体的控制要求对 ,
, 和b0进行调整,使系统的动静态性能达到最优。
和b0进行调整,使系统的动静态性能达到最优。
3 仿真研究
以某300 MW燃煤直流炉再热机组为研究对象。刘翔等[18]给出了该机组在100%负荷工作点处的线性化传递函数矩阵:

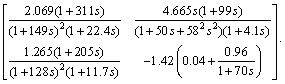

首先,对系统的开环动态特性进行分析,图5所示为该对象的开环单位阶跃响应曲线。

图5 机炉协调系统开环单位阶跃响应曲线
Fig. 5 Open-loop step responses of boiler-turbine unit
由图5可知:机炉协调系统两回路之间存在耦合,即燃烧率指令或汽机阀门开度指令的改变会引起汽机功率和主汽压力同时发生变化;此外,锅炉侧对象存在大惯性环节,动态响应速度较慢,在103 s数量级才能达到稳定。该大惯性环节的存在将使系统的稳定性降低,动态响应品质下降,控制难度加大[19]。
根据上述分析,为机炉协调系统设计柔性自抗扰控制方案,控制目标是使系统满足以下要求:
1) 功率输出能快速响应电网对负荷的需求。
2) 负荷变化时,机前主汽压力保持稳定,仅允许在小范围内波动。
3) 系统处于稳定工作点时,控制器能够有效地抑制系统中的各种扰动。
4) 机组大范围变工况时,控制器有足够强的鲁棒性维持系统稳定。
3.1 柔性因子确定
使功率回路的设定值Ns发生15 WM (5%负荷)的正向阶跃变化,令柔性因子 在(0 1)内取值,取值步长为0.1, 对应的系统输出及控制量曲线如图6和图7所示。
在(0 1)内取值,取值步长为0.1, 对应的系统输出及控制量曲线如图6和图7所示。
从图6和图7可见:当柔性因子 取不同值时,系统的输出响应和控制量指令有显著差异。为了选取最优的柔性因子,以两回路的ITAE之和作为性能评价标准。ITAE兼顾系统响应的快速性和稳定性,其表达式为
取不同值时,系统的输出响应和控制量指令有显著差异。为了选取最优的柔性因子,以两回路的ITAE之和作为性能评价标准。ITAE兼顾系统响应的快速性和稳定性,其表达式为


图6 系统输出响应曲线
Fig. 6 Output responses of system to setpoint change

图7 控制量曲线
Fig. 7 Curves of control input
其中:e(t)为设定值与输出值的误差; 为仿真时间。表1所示为柔性因子
为仿真时间。表1所示为柔性因子 取不同值时系统的ITAE。
取不同值时系统的ITAE。
表1 控制系统性能指标
Table 1 Performance indexes of control system
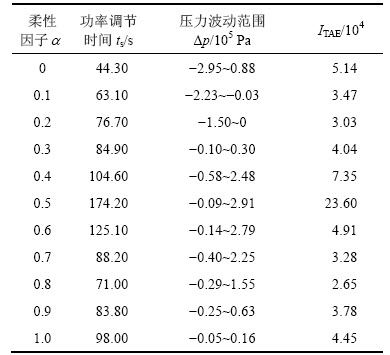
由图6、图7及表1可知:
1) 当 =0时,功率输出响应最迅速,但主汽压力波动最大。
=0时,功率输出响应最迅速,但主汽压力波动最大。
2) 当 时,随着
时,随着 增大,功率输出响应变慢,压力由负向波动变为正向波动,控制量波动剧烈。
增大,功率输出响应变慢,压力由负向波动变为正向波动,控制量波动剧烈。
3) 当 =0.5时,系统输出的动态特性最差。
=0.5时,系统输出的动态特性最差。
4) 当 时,随着
时,随着 增大,功率输出响应先变快后变慢,压力波动显著减小,控制量趋向平滑。
增大,功率输出响应先变快后变慢,压力波动显著减小,控制量趋向平滑。
5) 当 =0.8时,两回路ITAE最小,系统输出兼顾了快速性和稳定性,接近于能量供需平衡。
=0.8时,两回路ITAE最小,系统输出兼顾了快速性和稳定性,接近于能量供需平衡。
6) 当 =1.0时,功率输出响应平缓,主汽压力波动最小。
=1.0时,功率输出响应平缓,主汽压力波动最小。
因此,选取 =0.8为最优柔性因子,对应的ADRC参数见表2。
=0.8为最优柔性因子,对应的ADRC参数见表2。
表2 控制器参数
Table 2 Controller parameters

3.2 输入扰动实验
设系统处于额定工况下,在t =100 s时为燃烧率指令uB加入方波扰动d1=10 t/h,持续时间300 s,以模拟来自锅炉侧的干扰。图8所示为存在输入扰动时功率回路的扩张状态曲线,图9和图10所示分别为功率回路输出曲线和控制量曲线。
由图8~10可知:当燃烧率指令受到方波扰动时,ESO能对包括该扰动在内的扩张状态进行有效估计。在此基础上由控制率对该估计量进行补偿,可使ADRC具有很强的抵抗输入扰动的能力,保证输出尽快恢复稳定状态。

图8 ADRC中扩张状态曲线
Fig. 8 Curves of extended state in ADRC
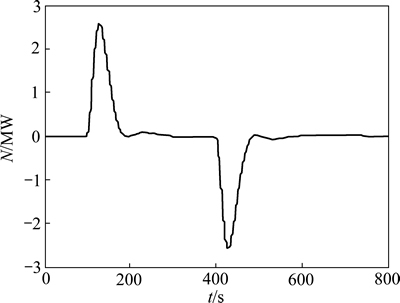
图9 额定功况下系统功率输出响应曲线
Fig. 9 Output response curve at full power

图10 额定工况下系统控制量曲线
Fig. 10 Control input curve at full power
3.3 变工况实验
单元机组的运行工况需要根据电网对负荷的需求进行相应调整。设计良好的控制系统应能保证机组在大范围变工况时维持稳定运行。除了满负荷运行外,70%负荷是单元机组的另一个常见工况点。本文研究的某300 MW燃煤直流炉再热机组在70%负荷点处的线性化传递函数矩阵为[18]



若针对不同工况分别设计控制器,则不仅极大地增加了控制系统的复杂性,而且需要解决无扰切换等问题。考虑到ADRC不依赖于对象精确模型,将基于100%工况整定的控制器直接用于70%工况。仿真中,在t=0 s时为功率回路加入正向阶跃设定值Ns=15 MW,系统输出响应曲线及控制量曲线如图11和12所示。
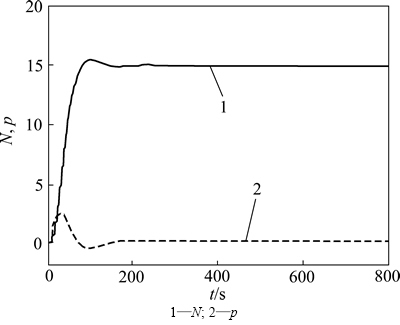
图11 70%工况下输出响应曲线
Fig. 11 Output responses at 70% of full power

图12 70%工况下控制量曲线
Fig. 12 Control inputs at 70% of full power
从图11和12可见:功率回路快速平稳地跟踪设定值的变化,机前主汽压力在较小范围内波动,控制量变化平滑,无抖振现象,可知基于100%工况设计的控制器用于70%工况时依然获得了良好的控制效果。其原因在于变工况产生的模型误差被作为扩张状态进行了有效估计,然后由控制量补偿,从而使ADRC具有较强的适应大范围变工况的能力。
3.4 蒙特卡罗实验
根据蒙特卡罗原理[20],使机炉协调系统的模型参数相对于标称值发生±10%的随机摄动,产生样本数量为500的被控对象族 ,以模拟可能存在的建模误差和模型参数不确定性等。将表2中的控制器参数作用于
,以模拟可能存在的建模误差和模型参数不确定性等。将表2中的控制器参数作用于 进行仿真实验,通过该组随机试验下控制指标的离散程度衡量控制器在对象存在不确定性时的鲁棒性。具体地,对
进行仿真实验,通过该组随机试验下控制指标的离散程度衡量控制器在对象存在不确定性时的鲁棒性。具体地,对 中各被控对象的功率回路加入正向阶跃设定值Ns=15 MW,2种工况下系统蒙特卡罗实验结果分别如图13和图14所示。
中各被控对象的功率回路加入正向阶跃设定值Ns=15 MW,2种工况下系统蒙特卡罗实验结果分别如图13和图14所示。
统计蒙特卡罗实验中功率回路的调节时间ts及系统ITAE,其分布如图15所示。
图15中,二维空间坐标分别表示调节时间ts和ITAE,实心和空心点集分别为100%工况和70%工况下摄动系统的性能指标分布。点集离原点越近,表明系统性能越好;越密集,表明鲁棒性越强。可见:所设计控制方案用于2个工况时,均具有很强的性能鲁棒性。由于该控制器参数为基于100%负荷模型整定的参数,因此,控制器在100%工况下的性能鲁棒性比70%工况下的鲁棒性强。

图13 满负荷工况下蒙特卡罗实验结果
Fig. 13 Monte-Carlo experiment results at full power

图14 70%负荷工况下蒙特卡罗实验结果
Fig. 14 Monte-Carlo experiment results at 70% of full power
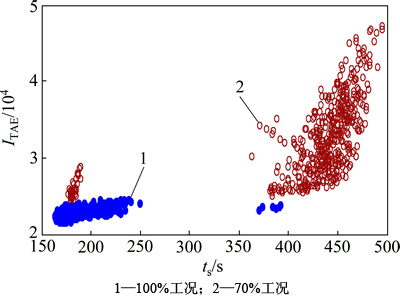
图15 摄动系统性能指标分布
Fig. 15 Distribution of performance index
4 结论
1) 为某300 MW燃煤直流炉再热机组设计柔性自抗扰控制方案并进行仿真研究。首先,以ITAE为评价基准确定最优柔性因子,使机炉协调系统接近能量供需平衡,然后设计自抗扰控制器对系统中的扰动、不确定性等因素进行有效估计和补偿。对机炉协调系统进行输入扰动实验、变工况实验和蒙特卡罗实验。
2) 柔性自抗扰控制方案综合了柔性控制结构和自抗扰控制器的优点:结构简单,解决了系统输出快速性和稳定性之间的矛盾;可以有效地抑制输入扰动;在大范围变工况和模型参数存在不确定性时具有很强的自适应能力和鲁棒性。该方案获得了良好的控制品质,具有工程应用价值。
参考文献:
[1] LI Yiguo, SHEN Jiong, Lee K Y, et al. Offset-free fuzzy model predictive control of a boiler-turbine system based on genetic algorithm[J]. Simulation Modelling Practice and Theory, 2012, 26(1): 77-95.
[2] Hamed M, Aria A, Gholamreza V. Nonlinear dynamics and control of bifurcation to regulate the performance of a boiler-turbine unit[J]. Energy Conversion and Management, 2013, 68(1): 105-113.
[3] Chen P. Multi-objective control of nonlinear boiler-turbine dynamics with actuator magnitude and rate constraints[J]. ISA transactions, 2013, 52(1): 115-128.
[4] Jalali A A, Golmohammad H. An optimal multiple-model strategy to design a controller for nonlinear processes: A boiler-turbine unit[J]. Computers & Chemical Engineering, 2012, 46(1): 48-58.
[5] FANG Fang, WEI Lei. Backstepping-based nonlinear adaptive control for coal-fired utility boiler–turbine units[J]. Applied Energy, 2011, 88(3): 814-824.
[6] YANG Shizhong, QIAN Chunjiang, DU Haibo. A genuine nonlinear approach for controller design of a boiler-turbine system[J]. ISA transactions, 2012, 51(3): 446-453.
[7] LIU Xiangjie, KONG Xiaobing. Nonlinear fuzzy model predictive iterative learning control for drum-type boiler-turbine system[J]. Journal of Process Control, 2013, 23(8): 1023-1040.
[8] WU Jie, Nguang S K, SHEN Jiong, et al. Robust H∞ tracking control of boiler-turbine systems[J]. ISA Transactions, 2010, 49(3): 369-375.
[9] TAN Wen, FANG Fang, TIAN Liang, et al. Linear control of a boiler-turbine unit: Analysis and design[J]. ISA Transactions, 2008, 47(2): 189-197.
[10] 于达仁, 翁一武, 王仲奇. 火电单元机组的柔性控制[J]. 中国电机工程学报, 2002, 22(7): 129-133.
YU Daren, WENG Yiwu, WANG Zhongqi. A study flexible control method for boiler-turbine units[J]. Proceedings of the CSEE, 2002, 22(7): 129-133.
[11] 夏元清, 黄焕袍, 韩京清. 不确定时滞系统ADRC控制[J]. 中南大学学报(自然科学版), 2003, 34(1): 383-385.
XIA Yuanqing, HUANG Huanpao, HAN Jingqing. ADRC control of uncertain systems with time-delay[J]. Journal of Central South University (Science and Technology), 2003, 34(1): 383-385.
[12] 赵志良. 非线性自抗扰控制的收敛性[D]. 合肥: 中国科学技术大学数学系, 2012: 57-60.
ZHAO Zhiliang. Convergence of nonlinear active disturbance rejection control[D]. Hefei: University of Science and Technology of China. Department of Mathematics, 2012: 57-60.
[13] YANG Xiaoxia, HUANG Yi. Capabilities of extended state observer for estimating uncertainties[C]// Proceedings of the American Control Conference. St Louis, United States, 2009: 3700-3705.
[14] GAO Zhiqiang. Scaling and bandwidth-parameterization based controller tuning[C]// Proceedings of the American Control Conference. Denver, United States, 2006: 4989-4996.
[15] 龙晓军, 于双和, 杨振强, 等. 基于自抗扰技术的永磁同步电机调速方法[J]. 中南大学学报(自然科学版), 2011, 42(1): 376-379.
LONG Xiaojun, YU Shuanghe, YANG Zhenqiang, et al. Speed regulation of permanent magnet synchronous motor based on active disturbance rejection control[J]. Journal of Central South University (Science and Technology), 2011, 42(1): 376-379..
[16] 王丽君, 童朝南, 李擎, 等. 热连轧板宽板厚的实用白抗扰解耦控制[J]. 控制理论与应用, 2012, 29(11): 1471-1478.
WANG Lijun, TONG Chaonan, LI Qing, et al. A practical decoupling control solution for hot strip width and gauge regulation based on active disturbance rejection[J]. Control Theory & Applications, 2012, 29(11): 1471-1478.
[17] WANG Qingguo, HUANG Bin, GUO Xin. Auto-tuning of TITO decoupling controllers from step tests[J]. ISA Transactions, 2000, 39(4): 407-418.
[18] 刘翔, 姜学智, 李东海, 等. 火电单元机组机炉协调自抗扰控制[J]. 控制理论与应用, 2001, 18(1): 149-152.
LIU Xiang, JIANG Xuezhi, LI Donghai, et al. Coordinated auto-disturbance-rejection control for boiler-turbine unit[J]. Control Theory and Applications, 2001, 18(1): 149-152.
[19] 张玉琼, 李东海. 一类沸腾式流化床系统的自抗扰控制[J]. 中国科学技术大学学报, 2012, 42(5): 391-397.
ZHANG Yuqiong, LI Donghai. Active disturbance rejection control on a bubbling fluidized bed[J]. Journal of University of Science and Technology of China, 2012, 42(5): 391-397.
[20] WANG Chuanfeng, LI Donghai, LI Zheng, et al. Optimization of controllers for gas turbine based on probabilistic robustness[J]. Journal of Engineering for Gas Turbines and Power, 2009, 131(5): 054502.1-054502.5.
(编辑 陈灿华)
收稿日期:2014-09-21;修回日期:2014-11-12
基金项目(Foundation item):国家自然科学基金资助项目(51176086) (Project(51176086) supported by the National Natural Science Foundation of China)
通信作者:李东海,博士,副教授,从事自抗扰控制理论及热工自动化研究;E-mail: lidongh@mail.tsinghua.edu.cn