具有低脆性参数的Zr-Al-Ni-Cu玻璃形成合金
来源期刊:中国有色金属学报(英文版)2013年第11期
论文作者:安伟科 熊 翔 刘 咏 蔡安辉 周果君 罗 云 李铁林 李小松
文章页码:3312 - 3317
Key words:Zr-Al-Ni-Cu alloy; metallic glass; fragility
摘 要:采用铜模铸造法制备出一系列Zr-Al-Ni-Cu块体非晶合金,其脆性参数值分别采用Arrhenius和Vogel-Fulcher-Tammann (VFT)方法进行计算。结果表明,这些非晶合金具有低的脆性参数值,其原因可能与网络状的微观结构有关。另外,Zr-Al-Ni-Cu合金的脆性参数值可以通过Zr含量进行调整,当Zr含量接近54%(摩尔分数)时,Zr-Al-Ni-Cu合金,即Zr54Al13Cu18Ni15合金的脆性参数值最小,约为13。
Abstract: Zr-Al-Ni-Cu bulk metallic glasses (BMGs) were developed and their fragility parameters (m) were calculated by Arrhenius and Vogel-Fulcher-Tammann (VFT) equations. The results show that the m values of the Zr-Al-Ni-Cu BMGs derived by Arrhenius equation are in agreement with the corresponding m values derived by VFT equation. These Zr-Al-Ni-Cu BMGs characterize in low m values. The low m values for these BMGs would be due to their network microstructures. In addition, the m values of Zr-Al-Cu-Ni BMGs could be obtained by regulating Zr content. The composition of Zr-Al-Cu-Ni BMGs with the lowest m value would be near 54%Zr (mole fraction) because the m value about 13 of Zr54Al13Cu18Ni15 BMG is the lowest among these Zr-Al-Ni-Cu BMGs developed.
Trans. Nonferrous Met. Soc. China 23(2013) 3312-3317
Wei-ke AN1, Xiang XIONG2, Yong LIU2, An-hui CAI1,2, Guo-jun ZHOU1, Yun LUO1, Tie-lin LI1, Xiao-song LI1
1. College of Mechanical Engineering, Hunan Institute of Science and Technology, Yueyang 414006, China;
2. State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China
Received 3 December 2012; accepted 17 June 2013
Abstract: Zr-Al-Ni-Cu bulk metallic glasses (BMGs) were developed and their fragility parameters (m) were calculated by Arrhenius and Vogel-Fulcher-Tammann (VFT) equations. The results show that the m values of the Zr-Al-Ni-Cu BMGs derived by Arrhenius equation are in agreement with the corresponding m values derived by VFT equation. These Zr-Al-Ni-Cu BMGs characterize in low m values. The low m values for these BMGs would be due to their network microstructures. In addition, the m values of Zr-Al-Cu-Ni BMGs could be obtained by regulating Zr content. The composition of Zr-Al-Cu-Ni BMGs with the lowest m value would be near 54%Zr (mole fraction) because the m value about 13 of Zr54Al13Cu18Ni15 BMG is the lowest among these Zr-Al-Ni-Cu BMGs developed.
Key words: Zr-Al-Ni-Cu alloy; metallic glass; fragility
1 Introduction
Up to now, many kinds of bulk metallic glasses have been developed including Mg-, La-, Zr-, Ti-, Cu-, Nd-, Fe-, Pr-, Pd-, Ce-, Ca-, and other rare earth-based [1-5]. Among them, Zr-based bulk metallic glasses can be produced by the conventional casting process, leading to successful applications as sporting goods, surgical instruments and electronic devices. The applications of metallic glasses require high stability in various environments in order to ensure an acceptable lifetime. The metallic glasses are metastable materials. With increase of temperature, such non-crystalline systems transform into crystalline state in course of time. From the technological application point of view, the thermal stability of the metallic glasses is of considerable importance. The fragility parameter m can be used to estimate the thermal stability and/or glass forming ability (GFA) of metallic glass. In addition, the m has been used to segregate glass forming materials into three general categories: strong, intermediate and fragile liquids [6,7]. For strong liquids, m is less than 30 with a lower limit of about 16. For example, the rigid tetrahedral network oxides SiO2 and GeO2 have m value of 20 at glass transition temperature Tg [7]. In contrast, fragile liquids such as polymers and ionic melts which have thermally sensitive structures that can be easily disrupted by small increase in temperature display large values of m≥100. In the case of metallic glasses, a previous compilation of the m for a range of ternary and higher-order alloys indicated an intermediate fragility strength where 30
In the present work, a family of BMGs consisting of conventional metallic components Zr, Al, Ni, and Cu was obtained. Through compositional modification, Zr-Al-Ni-Cu ternary BMGs with relative low m values, even lower than 16 were developed.
2 Experimental
2.1 Composition design
CHEN et al [10] noticed that the known amorphous phases in Zr-Al-Ni, Zr-Al-Cu, and Zr-Al-Ni-Cu systems all have e/a=∑CiEi (Ci and Ei are atomic fraction and conduction electron concentration of the ith element, respectively) ratios in the range of 1.3-1.5 close to the value of 1.4 of Inoue alloy and average atomic radius Ra=∑CiRi (Ri is atomic radius of the ith element) in the range of 0.1487-0.1533 nm close to 0.1496 nm of Inoue alloy. They determined that the conduction electron concentrations for Zr, Al, Ni and Cu are 1.5, 3, 0, and 1.0, respectively. Then a group of Zr-Al-Ni-Cu glass forming alloys was designed by e/a=1.4, Ra=0.1496 nm, and ∑Ci=1 by adding a suitable cluster. However, it is difficult for selecting a suitable cluster in multi-component alloys. A large quantity of direct and indirect evidence [11-16] shows topological and chemical short-range order (SRO) in amorphous alloy. Compositional difference, even minor addition can change the magnitude, type and distribution of SRO [14,15], which influences the relaxation, diffusion and rearrangement of atoms, resulting in the change of GFA and thermal stability of glass forming alloys [16]. In addition, better GFA and thermal stability of glass forming alloy are achieved for the rationalization of the combination of the magnitude, type and distribution of SRO [16]. The microstructure of metallic glass inherits from the melt. The magnitude, category, and stability of SRO are related with the binding force among atoms. It is well known that the melting heat ΔHm can be used to characterize the binding force. In addition, we found that the Zr-Al-Ni-Cu system had optimum GFA when the melting heat ΔHm=∑CiΔHmi (ΔHmi is the melting heat of the ith element) was near 19.7146 kJ/mol [17]. A group of Zr-Al-Ni-Cu glass forming alloys is designed by merging the ΔHm condition with three afore-mentioned conditions. It must be noticed that the ΔHm constraint condition is not strong but weak. If the ΔHm constraint condition is strong, the composition is unique. On the other hand, if the ΔHm constraint condition is weak, there are many finite compositions satisfying with four conditions. The constraint conditions for Zr-Al-Ni-Cu glass forming alloys are: e/a=1.38, da=0.1500 nm and ΔHm≈19 kJ/mol for Zr54Al13Cu18Ni15; e/a=1.38, da=0.1486 nm and ΔHm≈19.7 kJ/mol for other Zr-Al-Ni-Cu alloys. The detailed compositions for Zr-Al-Ni-Cu alloys are listed in Table1.
2.2 Experimental procedures
Pre-alloyed Zr-Al-Ni-Cu ingots with nominal compositions (mole fraction, %), as shown in Table 1, were prepared by arc melting of the pure elements: Zr (99.99%), Ni (99.99%), Cu (99.99%), and Al (99.99%) under a Ti-gettered argon atmosphere. The ingots were remelted five times in order to obtain homogeneity and finally cylindrical rods with 2 mm in diameter were prepared from the pre-alloyed ingots by suction casting into a water-cooled copper mould.
2.3 Testing methods
The structure of the as-cast samples was characterized by X-ray diffraction (XRD) using an XD-3Adiffractometer with Cu Kα and transmission electron microscopy (TEM) using a JEM2000EX instrument operated at 160 kV, respectively. The microstructure was investigated by an SIRION scanning electronic microscope (SEM) operated at 20 kV. The energy dispersive spectrometry (EDS) system was combined with the TEM. The microhardness was performed using an HVI-10A microhardness tester under a load of 1.47 kN for a dwell time of 30 s. Thermal analysis was carried out using DSC-404C differential scanning calorimeter at heating rates of 0.25, 0.33, 0.5 and 0.67 ks-1, respectively.
3 Results and discussion
Figure 1 shows that these glass forming alloys can be cast into entirely glassy rods with diameter of 2 mm without any apparent crystalline Bragg peaks. Clear glass transitions and sharp crystallization events are observed in the DSC traces (Fig. 2), confirming the glassy nature of these BMGs. The thermal parameters are also summarized in Table 1.
Table 1 Glass transition temperature Tg, undercooled liquid region ΔTx, fragility parameters mA and mv for Zr-based metallic glasses


Fig. 1 XRD patterns for Zr-Al-Ni-Cu glass forming alloys

Fig. 2 DSC curves for Zr-Al-Ni-Cu glass forming alloys
For glass forming liquids, the temperature dependence of η on the temperature intervals between Tm and Tg can be described by the Vogel-Fulcher-Tammann (VFT) equation [25]:
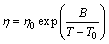 (1)
(1)
where η0, B and T0 are fitting parameters and T is the temperature. Often over a narrower temperature range, especially near Tg, η(T) can also be approximated very well by an Arrhenius equation where T0=0 in Eq. (1), and is given by
 (2)
(2)
where Ea is an activation energy and R is the gas mole constant.
For some liquids, such as SiO2 and GeO2 which have a three-dimensional tetrahedral network structure, the Arrhenius law can be used to fit η(T) over the entire temperature range between Tm and Tg [26]. All other glass forming liquids exhibit varying degrees of departure from Arrhenius behavior. Strong liquids are those with an Arrhenius temperature dependent of the viscosity, while fragile liquids are more sensitive to thermal changes and display large deviations from Arrhenius behavior. In order to quantify the fragility (the degree of departure from an Arrhenius temperature dependence),  et al [6,27] introduced a fragility parameter m defined as
et al [6,27] introduced a fragility parameter m defined as
 (3)
(3)
where τ(T) is relaxation time. Since the viscosity is proportional to a structural relaxation time, m can be estimated by replacing τ(T) with η(T) in Eq. (3). The fragility parameter m is then a measure of the steepness of the slope of the viscosity curve at Tg when the temperature is scaled by Tg. If η(T) can be described by the Arrhenius equation, then,
 (4)
(4)
On the other hand, values of fragility can be directly taken by the VFT equation fitting to viscosity data [7]. The liquid fragility can be determined from a purely thermodynamic way near Tg, and the m estimated by this method is consistent with that obtained by the kinetic method [28]. Since viscosity relaxation and the glass transition measured by calorimetric methods occur on the same time scale, the dependence of heating rate β on glass transition can be used as an alternative way to determine the fragility of the glasses [3,28-34]. Previous studies confirm that the β dependent on Tg describes the fragility equally well as complementary viscosity measurements [31]. Therefore, the dependence of Tg on β can also be described by a VFT-type relation:
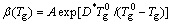 (5)
(5)
where A is a constant, 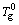 is the VFT temperature, and D* is the strength parameter. From the relationship between Tg and β of the metallic glasses using the VFT equation, the VFT parameters A,
is the VFT temperature, and D* is the strength parameter. From the relationship between Tg and β of the metallic glasses using the VFT equation, the VFT parameters A,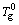 , and D* are obtained. Then m can be obtained as
, and D* are obtained. Then m can be obtained as
 (6)
(6)
Although the uncertainty of the values of 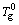 and D* is quite large, the change of
and D* is quite large, the change of 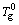 results in change of D*, which keeps the m value reasonably constant [28-33]. The relationship between Tg and β was fitted with the VFT equation. From the best fit according to Eqs. (5) and (6), the m values (mv) for Zr-Al-Cu-Ni are shown in Table 1. On the other hand, the m values (mA) calculated by Eq. (4) at the heating rate of 0.33 ks-1 are also listed in Table 1. Obviously, the mA and mv values are consistent with each other although the mA deviates from the mv for Zr62.5Al12.1Cu7.95Ni17.45. In addition, the mv values for these Zr-Al-Ni-Cu BMGs are less than 36. Among them, the mv values for Zr54Al13Cu18Ni15, Zr61.5Al10.7Cu13.65Ni14.15, Zr64Al10.1Cu11.7Ni14.2 and Zr63.5Al10.7Cu10.7Ni15.1 BMGs are less than 20. Especially, the mv values for Zr54Al13Cu18Ni15 and Zr61.5Al10.7Cu13.65Ni14.15 BMGs are less than 16. This indicates that these Zr-Al-Ni-Cu BMGs have the similar microstructure to SiO2 and GeO2. As shown in Fig. 1, a high halo about 2θ=20°appears which is smaller than that of other Zr-Al-Ni-Cu metallic glasses (2θ=40-50°) [10,14,15,32,18-20,23]. If the average distance d between the atoms is estimated by
results in change of D*, which keeps the m value reasonably constant [28-33]. The relationship between Tg and β was fitted with the VFT equation. From the best fit according to Eqs. (5) and (6), the m values (mv) for Zr-Al-Cu-Ni are shown in Table 1. On the other hand, the m values (mA) calculated by Eq. (4) at the heating rate of 0.33 ks-1 are also listed in Table 1. Obviously, the mA and mv values are consistent with each other although the mA deviates from the mv for Zr62.5Al12.1Cu7.95Ni17.45. In addition, the mv values for these Zr-Al-Ni-Cu BMGs are less than 36. Among them, the mv values for Zr54Al13Cu18Ni15, Zr61.5Al10.7Cu13.65Ni14.15, Zr64Al10.1Cu11.7Ni14.2 and Zr63.5Al10.7Cu10.7Ni15.1 BMGs are less than 20. Especially, the mv values for Zr54Al13Cu18Ni15 and Zr61.5Al10.7Cu13.65Ni14.15 BMGs are less than 16. This indicates that these Zr-Al-Ni-Cu BMGs have the similar microstructure to SiO2 and GeO2. As shown in Fig. 1, a high halo about 2θ=20°appears which is smaller than that of other Zr-Al-Ni-Cu metallic glasses (2θ=40-50°) [10,14,15,32,18-20,23]. If the average distance d between the atoms is estimated by
 (7)
(7)
where θ and λ are angle and wavelength of incident ray, respectively. Then, the d values of the studied Zr-Al-Ni-Cu metallic glasses are about 2 times those of other Zr-Al-Ni-Cu metallic glasses. This indicates that the size of the short and/or medium range orders of studied Zr-Al-Ni-Cu metallic glasses is 2 times larger than other Zr-Al-Ni-Cu metallic glasses, resulting in that these orders can be observed. Thus the cross-sections of all Zr-Al-Ni-Cu metallographic specimens are etched with 20% hydrofluoric acid solution. Figure 3(a) shows a typical microstructure of Zr61.5Al10.7Cu13.65Ni14.15 metallic glass. We can clearly observe a network structure which is due to not the corrosive cracking but the dissolution of the alloy elements because no cracks are observed (see Figs. 3(b) and (c)). In addition, we can clearly observe from Figs. 4(a) and (c) that the network structure does not show the characteristics of the crack. Microhardness tests are conducted on the “matrix” and vicinity of the “network”, as shown in Figs. 3(b) and (c). The different hardnesses are clearly seen from the different sizes of two indentations. It would be due to the different contents of the alloying elements, resulting in the different corrosion resistances and different dissolution rates.

Fig. 3 Typical network-like microstructure (a) and indentation of Zr61.5Al10.7Cu13.65Ni14.15 metallic glass (b, c)
The selected-area electron diffraction SAED patterns (the inset of Figs. 4(a) and (b)) for Zr61.5Al10.7- Cu13.65Ni14.15 indicate the amorphous states not only for the matrixes but also for the networks without the observation of the diffraction dots for the crystalline phase.
As shown in Figs. 4(c) and (d), although the number of elements is the same for the matrix and the network, the content of alloy elements for the matrix is different from that for the network. The difference of the content of alloy elements is the largest for Zr, namely, the content of Zr is more in the matrix than in the network, resulting in the difference of the corrosion resistance between the matrix and the network. It is also indirectly proved by different hardnesses, as shown in Figs. 3(b) and (c). Recently, LIU et al [35] found that the size and distribution of B2 CuZr particles can be effectively homogenized by Ta addition in rapidly solidified Cu47Zr48-xAl5Tax (0≤x≤1%, mole fraction) alloys. This indicates that a regular distribution of the alloying elements appears when the content of the alloying elements arrives at a rational value. Thus, the network structure results in a lower m for Zr-Al-Ni-Cu BMGs investigated. The small value of m is considered to be one of the empirical rules for designing the BMG formers whose metastable-equilibrium supercooled liquid is fairly stable [32]. The afore-mentioned results indicate the better GFA [17,36] and thermal stability for the investigated Zr-Al-Ni-Cu BMGs. As shown in Table 1, the undercooled liquid region ΔTx of the investigated Zr-Al-Ni-Cu BMGs is more than that of Zr41Ti14Ni10Cu12.5Be22.5 [18,19], and the m of the former is smaller than that of the latter, indicating that the thermal stability of the former is better than that of the latter. In addition, we compared the investigated Zr-Al-Ni-Cu BMGs with other Zr-based BMGs [5,23,20], as shown in Table 1. One can observe that the m value of Zr-Al-(Cu, Ni) BMGs is the same when Zr content is 65%. Otherwise, the m value of Zr-Al-(Cu,Ni) BMGs less than 65% Zr is smaller than that of Zr-Al-(Cu,Ni) BMGs with 65% Zr. Especially, the m decreases down to the smallest when the Zr content decreases down to 54%. This indicates that Zr-Al-(Cu,Ni) BMGs with the low m could be obtained by regulating the Zr content and the composition of Zr-Al-(Cu,Ni) BMGs with the lowest m is near 54%Zr. These phenomena are necessary for further investigation.

Fig. 4 SEM images (a, b) and EDS results for areas A (c) and B (d) of Zr61.5Al10.7Cu13.65Ni14.15 metallic glass (The insets are selected-area electron diffraction patterns of A (a) and selected-area electron diffraction pattern for B (b), respectively
4 Conclusions
1) A series of Zr-Al-Ni-Cu BMGs are developed and characterized in low fragility parameter values. The fragility parameter values of these BMGs are between 13 and 36.
2) The low fragility parameter values of these BMGs would be due to their network microstructures. Zr-Al-Cu-Ni BMGs with the low fragility parameter values could be obtained by regulating the Zr content. The composition of Zr-Al-Cu-Ni BMGs with the lowest fragility parameter value is near 54%Zr.
References
[1] KHADEMIAN N, GHOLAMIPOUR R. Effects of infiltration parameters on mechanical and microstructural properties of tungsten wire reinforced Cu47Ti33Zr11Ni6Sn2Si1 metallic glass matrix composites [J]. Transactions of Nonferrous Metals Society of China, 2013, 23: 1314-1321.
[2] CAI An-hui, XIONG Xiang, LIU Yong, AN Wei-ke, ZHOU Guo-jun, LUO Yun, LI Tie-lin, LI Xiao-song. A Cu-based bulk amorphous composite reinforced by carbon nanotube [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(9): 2191-2197.
[3] ZHANG B, WANG R J, ZHAO D Q, PAN M X, WANG W H. Properties of Ce-based bulk metallic glass-forming alloys [J]. Phys Rev B, 2004, 70: 224208.
[4] WANG W H. Roles of minor additions in formation and properties of bulk metallic glasses [J]. Prog Mater Sci, 2007, 52: 540-596.
[5] WANG W H, DONG C, SHEK C H. Bulk metallic glasses [J]. Mater Sci Eng R, 2004, 44: 45-89.
[6]  R, NGAI K L, ANGELL C A, PLAZEK D J. Nonexponential relaxations in strong and fragile glass formers [J]. J Chem Phys, 1993, 99: 4201-4209.
R, NGAI K L, ANGELL C A, PLAZEK D J. Nonexponential relaxations in strong and fragile glass formers [J]. J Chem Phys, 1993, 99: 4201-4209.
[7] ANGELL C A. Formation of glasses from liquids and biopolymers [J]. Science, 1995, 267: 1924-1935.
[8] PERERA D N. Compilation of the fragility parameters for several glass-forming metallic alloys [J]. J Phys: Condens Mater, 1999, 11: 3807-3812.
[9] WANG W H. Correlations between elastic moduli and properties in bulk metallic glasses [J]. J Appl Phys, 2006, 99: 093506.
[10] CHEN W, WANG Y, QIANG J, DONG C. Bulk metallic glasses in the Zr-Al-Ni-Cu system [J]. Acta Mater, 2003, 51: 1899-1907.
[11] CHEN G L, HHUI X D, FAN S W, KOU H C, YAO K F. Concept of chemical short range order domain and the glass forming ability in multicomponent liquid [J]. Intermetallics, 2002, 10: 1221-1232.
[12] DOVE J P K, MEYER L. Mapping the magic numbers in binary Lennard-Jones clusters [J]. Phys Rev Lett, 2005, 95: 063401.
[13] HUFNAGEL T C, BRENNAN S. Short- and medium-range order in (Zr70Cu20Ni10)90-xTaxAl10 bulk amorphous alloys [J]. Phys Rev B, 2003, 67: 014203.
[14] LUO W K, SHENG H W, ALAMGIR F M, BAI J M, HE J H, MA E. Icosahedral short-range order in amorphous alloys [J]. Phys Rev Lett, 2004, 92: 145502.
[15] SAIDA J, INOUE A. Icosahedral quasicrystalline phase formation in Zr–Al–Ni–Cu glassy alloys by the addition of V, Nb and Ta [J]. J Non-Cryst Solids, 2002, 312-314: 502-507.
[16] KO H S, CHANG J Y. Effect of short-range order in liquid on the glass forming ability of Fe–Si–B alloy wires [J]. Mater Lett, 2004, 58: 1012-1016.
[17] CAI A H, CHEN H, AN W K, TAN J Y, ZHOU Y. Relationship between melting enthalpy ΔHm and critical cooling rate Rc for bulk metallic glasses [J]. Mater Sci Eng A, 2007, 457: 6-12.
[18] BUSCH R, KIM Y J, JOHNSON W L. Thermodynamics and kinetics of the undercooled liquid and the glass transition of the Zr41.2Ti13.8Cu12.5Ni10.0Be22.5 alloy [J]. J Appl Phys, 1995, 77: 4039-4044.
[19] BUSCH R, JOHNSON W L. The kinetic glass transition of the Zr46.75Ti8.25Cu7.5Ni10Be27.5 bulk metallic glass former-supercooled liquids on a long time scale [J]. Appl Phys Lett, 1998, 72: 2695-2697.
[20] WANIUK T A, BUSCH R, MASUHR A, JOHNSON W L. Equilibrium viscosity of the Zr41.2Ti13.8Cu12.5Ni10Be22.5 bulk metallic glass-forming liquid and viscous flow during relaxation, phase separation, and primary crystallization [J]. Acta Mater, 1998, 46: 5229-5236.
[21] LU Z P, TAN H, LI Y, NG S C. The correlation between reduced glass transition temperature and glass forming ability of bulk metallic glasses [J]. Scripta Mater, 2000, 42: 667-673.
[22] LU Z P, LI Y, NG S C. Reduced glass transition temperature and glass forming ability of bulk glass forming alloys [J]. J Non-Cryst Solids, 2000, 270: 103-114.
[23]  U, MEINHARDT J, ROOS S, LIEBERTZ H. Formation of quasicrystals in bulk glass forming Zr–Cu–Ni–Al alloys [J]. Appl Phys Lett, 1996, 69: 179-181.
U, MEINHARDT J, ROOS S, LIEBERTZ H. Formation of quasicrystals in bulk glass forming Zr–Cu–Ni–Al alloys [J]. Appl Phys Lett, 1996, 69: 179-181.
[24] LU Z P, LIU C T. Glass formation criterion for various glass-forming systems [J]. Phys Rev Lett, 2003, 91: 115505.
[25] SCHERER G W. Editorial comments on a paper by Gordon S. Fulcher [J]. J Am Ceram Soc, 1992, 75: 1060-1062.
[26] ANGELL C A, SICHINA W. Thermodynamics of the glass transition: Empirical aspects [J]. Annals of the New York Academy of Sciences, 1976, 279: 53-62.
[27]  R, ANGELL C A. Correlations of the nonexponentiality and state dependence of mechanical relaxations with bond connectivity in Ge-As-Se supercooled liquids [J]. Phys Rev B, 1992, 45: 10091-10094.
R, ANGELL C A. Correlations of the nonexponentiality and state dependence of mechanical relaxations with bond connectivity in Ge-As-Se supercooled liquids [J]. Phys Rev B, 1992, 45: 10091-10094.
[28] ITO K, MOYNIHAN C T, ANGELL C A. Thermodynamic determination of fragility in liquids and a fragile-to-strong liquid transition in water [J]. Nature, 1999, 398: 492-495.
[29] ZHAO Z F, ZHAO D Q, WANG W H. A highly glass-forming alloy with low glass transition temperature [J]. Appl Phys Lett, 2003, 82: 4699-4702.
[30] BRUNING R, SAMWER K. Glass transition on long time scales [J]. Phys Rev B, 1992, 46: 11318-11322.
[31] BUSCH R, BAKKE E, JOHNSON W L. Viscosity of the supercooled liquid and relaxation at the glass transition of the Zr46.75Ti8.25Cu7.5Ni10Be27.5 bulk metallic glass forming alloy [J]. Acta Mater, 1998, 46: 4725-4732.
[32] SHADOWSPEAKER L, BUSCH R. On the fragility of Nb-Ni-based and Zr-based bulk metallic glasses [J]. Appl Phys Lett, 2004, 85: 2508-2511.
[33] BORREGO J M, CONDE A, ROTH S, ECKERT J. Glass-forming ability and soft magnetic properties of FeCoSiAlGaPCB amorphous alloys [J]. J Appl Phys, 2002, 92: 2073-2078.
[34] YU B, BAI H Y. Excellent glass-forming ability in simple Cu50Zr50-based alloys [J]. J Non-Cryst Solids, 2005, 351: 1328-1332.
[35] LIU Z Q, LI R, LIU G, SU W H, WANG H, LI R, SHI M J, LUO X K, WU G J, ZHANG T. Microstructural tailoring and improvement of mechanical properties in CuZr-based bulk metallic glass composites [J]. Acta Mater, 2012, 60: 3128-3139.
[36] CAI A H, XIONG X, LIU Y, LI J H, AN W K, LUO Y. Characteristics of near-eutectic and off-eutectic Zr–Al–Ni–Cu glass forming alloys [J]. Mater Sci Eng A, 2009, 516: 100-102.
安伟科1,熊 翔2,刘 咏2,蔡安辉1,2,周果君1,罗 云 1,李铁林1,李小松1
1. 湖南理工学院 机械工程学院,岳阳 414006;
2. 中南大学 粉末冶金国家重点实验室,长沙 410083
摘 要:采用铜模铸造法制备出一系列Zr-Al-Ni-Cu块体非晶合金,其脆性参数值分别采用Arrhenius和Vogel-Fulcher-Tammann (VFT)方法进行计算。结果表明,这些非晶合金具有低的脆性参数值,其原因可能与网络状的微观结构有关。另外,Zr-Al-Ni-Cu合金的脆性参数值可以通过Zr含量进行调整,当Zr含量接近54%(摩尔分数)时,Zr-Al-Ni-Cu合金,即Zr54Al13Cu18Ni15合金的脆性参数值最小,约为13。
关键词:Zr-Al-Ni-Cu合金;非晶合金;脆性
(Edited by Xiang-qun LI)
Foundation item: Project (50874045) supported by the National Natural Science Foundation of China; Projects (200902472, 20080431021) supported by the China Postdoctoral Science Foundation; Project (10A044) supported by the Research Foundation of Education Bureau of Hunan Province of China
Corresponding author: An-hui CAI; Tel: +86-730-8648848; E-mail: cah1970@sohu.com
DOI: 10.1016/S1003-6326(13)62869-1

