摆线齿准双曲面齿轮的动态啮合性能

严宏志，刘明，王祎维

(中南大学 高性能复杂制造国家重点实验室，湖南 长沙，410083)

摘要：针对摆线齿准双曲面齿轮在空挡运行时发出尖啸声并伴有严重磨损的问题，通过动力学仿真分析的方法，对正车、倒车、空挡后退、空挡前行这几种工况下的齿轮的传动误差、角加速度的时域和频域图，以及正车和倒车在不同负载和转速下的角加速度和噪声的变化进行分析。研究结果表明：在正车工况下，也即是小轮的凹面驱动大轮的凸面的情况下，摆线齿准双曲面齿轮系统的噪声低，所受负载小，啮合动态性能最好；空挡时动态啮合性能较差，对齿轮损害较大。本文研究可为面向综合啮合性能的摆线齿准双曲面齿轮的设计提供依据。

关键词：摆线齿准双曲面齿轮；振动特性；传动误差；噪声

中图分类号：TH132.41          文献标志码：A         文章编号：1672-7207(2013)10-4026-07

Dynamic meshing performance of cycloid hypoid gear

YAN Hongzhi, LIU Ming, WANG Yiwei

(State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha 410083, China)

Abstract: For the scream noise and the severe wear issues of the cycloid tooth hypoid gears in neutral running, this project studied the gear transmission error, temporal and spectral characteristics of the angular acceleration with conditions of advancing, retreating or hang gap using dynamics simulation, as well as the analysis of the acceleration, and noise under different load and speed. The results show that the meshing noise and the contact pressure of the cycloid hypoid gears are smaller, and the meshing performance is optimal in driving forward state. However, the dynamic performance is poor at hand gap state. The data from these studies provide some design basis of the cycloid hypoid gears.

Key words: cycloid hypoid gear; vibrational chavacteristic; transmission error; noise

摆线齿准双曲面齿轮与弧齿准双曲面齿轮相比，由于采用连续分度法加工，具有生产效率高、易于干切屑、啮合性能好的特点，近几年已在车辆及其他装备中得到越来越多的应用。侯旭明等^[1]针对某车桥制造厂提出的摆线齿螺旋锥齿轮反车面出现严重磨损的情况，对其正、反车啮合特性进行分析，为摆线齿螺旋锥齿轮的优化提供依据。围绕获得齿轮平稳、长寿命传动等特性，国内外学者在齿轮啮合动态性能方面开展了大量的研究^[2-4]。Kahraman等^[5]以渐开线圆柱齿轮为对象，首先提出并求解了一个具有间隙、且包含传动误差参数激励的振动方程。虽然这个模型仍是常刚度的单自由度模型，但通过谐波平衡法求解，发现了跃迁频率、亚谐波共振及混沌现象。杨宏斌等^[6]建立了单自由度准双曲面齿轮的振动方程，这个方程包含着时变啮合刚度、传动误差和间隙，并用打靶法和连续参数化方法求解，得到了频响曲线。王三民等^[7-8]针对弧齿锥齿轮动态相对传动误差、齿面侧隙和时变啮合刚度等因素的影响，建立了7自由度的非线性振动方程。获得了不同工况下弧齿锥齿轮系统的扭转、横向及轴向的振动位移和速度，发现随着啮合频率的变化，系统经倍周期分岔进入混沌，并存在跳跃现象。Cheng等^[9]建立了一个包括时变啮合刚度、传动误差和间隙等具有14个自由度的方程。其研究认为传动误差是振动的主要激振源，并研究了动态响应，发现了亚谐波共振及在轻载情况下齿面间隙引起的跳跃现象。摆线齿锥齿轮啮合特性对于其自身及装备的使用寿命及性能有重要影响，本文作者拟采用有限元方法对线齿准双面齿轮啮合特性进行分析，研究摆线准双曲面齿轮在各个工况下的振动、噪声特性，为兼具非工作面优良啮合特性的摆线齿准双曲面齿轮优化设计提供依据。

1  摆线齿准双曲面齿轮啮合动力学建模

(1) 摆线齿准双曲面齿轮副几何模型。将在Pro/E环境下装配好的摆线齿准双面齿轮实体模型通过公共文件接口导入ADAMS中，加入齿轮轴的旋转运动副。大轮的齿数z₂=47，小轮的齿数z₁=11。

(2) 材料参数及接触定义。齿面之间的接触力采用基于impact函数的实体碰撞接触模型，根据文献[10-11]，知道实体碰撞接触为体对体，得到接触参数见表1。最终得到准双曲面齿轮的虚拟样机模型，如图1所示。

表1  接触参数表

Table 1  Contact parameter table

图1  齿轮传动模型

Fig. 1  Gear transmission model

(3) 载荷条件。根据车桥实际应用情况，拟从4种工况(见表2)对摆线齿准双面齿轮啮和特性进行分析。

表2  不同工况下的载荷约束参数

Table2  Load restraint parameters under different conditions.

2  啮合特性仿真分析

2.1  不同传动工况角加速度分析

按照表2的工况给系统添加载荷和约束，得到4种工况下从动轮的角加速度随时间变化历程图和频谱图，见图2。

齿轮啮合频率公式^[12]为

               (1)

其中：f_z为啮合频率，Hz；N为齿轮的转速，r/min；z为齿数。通过表1数据，并经计算得到f_z=183.33 Hz。

首先，从时域图来看各种工况下角加速度有效值的大小。从图2的时域图可知：整个角加速度图围绕0 rad/s²上下波动，这是由齿轮传动周期性的内部激励引起的。为了便于与图2(a)和图2(b)进行比较，将图2(c)和图2(d)的均方根值缩小(齿轮传动比)4.273倍，得到表3，可知从工况1到工况4，角加速度有效值成递增趋势，说明工况1的角加速度有效值最小，故其振动最小。

其次，从频域图上看，图2(a)~(d)所示为首个主率为啮合频率183.33 Hz。图2(a)加速度在一倍频处达到最大值，接着在三倍频和五倍频有主峰；图2(b)所示为加速度在二倍频处达到最大值，另外出现一倍频、三倍频、四倍频和五倍频的主峰；图2(c)所示为加速度在二倍频处达到最大值，在一倍频和四倍频处有主峰；图2(d)所示为加速度在三倍频处达到最大值，在一倍频和二倍频处有主峰。可知：空挡时角加速度频率幅值远大于正车或倒车驱动时频率幅值，说明空挡时振动程度要大得多；正车或倒车驱动时激发出了较空挡时高的频率的振动。

图2  从动轮角加速度时域和频谱图

Fig. 2  Driven wheel angular acceleration of time domain and frequency spectrum

表3  不同工况下角加速度特性

Table3  Angular acceleration characteristics under different conditions          rad/s²

2.2  不同负载下正车面与倒车面啮合性能分析

仿真的不同转速和负载参数见表4，仿真得到每种工况下的角加速度有效值(也即是均方根值)，见图3和图4。从图3和图4可知：在相同转速下正车面和倒车面的角加速度有效值随着阻力负载的增大而增大，倒车面的增大量大于正车面；在相同负载下正车面和倒车面的角加速度有效值随着驱动转速的增大而增大，倒车面的增大量大于正车面的增大量。因此，倒车面的传动性能不如正车面的传动性能，也即是其不能作为长期运行工作面的缘故。

表4  不同工况下里面负载及转速的设置

Table4  Setting of speed and load under different operating conditions

2.3  齿轮结构噪声分析

通过准双曲面齿轮系统的动态分析，根据表4的工况参数在ADAMS里面仿真后得到齿轮振动加速度周向和径向的时域响应曲线。再经过FFT变换，得到频域响应曲线。然后进行1/3倍频程处理，就可以得到各计算点加速度级1/3频程结构噪声值。加速度级1/3倍频程结构噪声值定义^[13]为：

            (2)

式中：L_a为加速度级1/3倍频程结构噪声，dB；a为以某一频率为中心频率的频率段的加速度有效值，m/s²；a₀为基准加速度，a₀=1×10^{-6 m/s2}。

齿轮系统在啮合频率附近振动相对激烈。这里仅研究啮合频率附近的加速度幅值级噪声，对相同驱动速度、相同负载转矩下正车和倒车面造成的噪声进行分析。由式(1)可得到：800，1 000和1 200 r/min对应的啮合频率为146.67，183.33和220.00 Hz。根据式(2)计算表5~ 7加速度幅值对应的噪声，结果见图5~8。由图5~8可知：倒车面噪声总是大于正车面噪声，随着驱动转速的增加，噪声强度增加；在同一转速下，随着阻力载荷的增加，噪声强度先增加后渐渐减少，主要是载荷越大齿面变形越大，齿轮的重合度越高，啮合冲击减少，噪声强度降低。

图3  从动轮角加速度与其负载阻力的关系

Fig. 3  Relationship between driven wheel angular acceleration and its load resistance

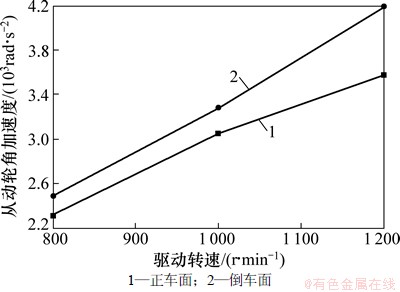
图4  从动轮角加速度与驱动轮转速的关系(1.025 kN·m)

Fig. 4  Relationship between driven wheel angular acceleration and driving wheel speed

表5  146.67 Hz下的加速度幅值

Table5  Acceleration amplitude at 146.67 Hz  10^{-4 m/s2}

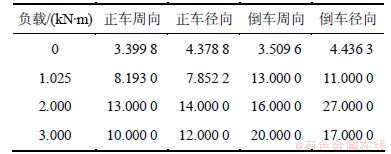
表6  183.33 Hz下的加速度幅值

Table6  Acceleration amplitude at 183.33 Hz  10^{-4 m/s2}

表7  220.00 Hz下的加速度幅值

Table7  Acceleration amplitude at 220.00 Hz  10^{-4 m/s2}

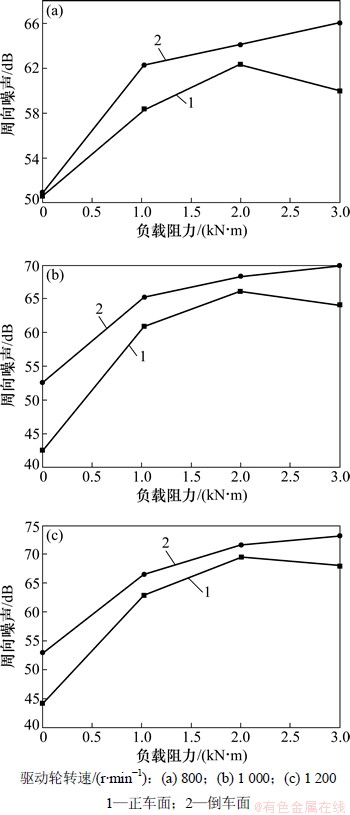
图5  周向噪声与负载的关系

Fig. 5  Relationship between circumference noise and load resistance

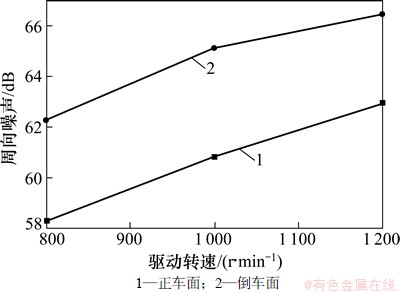
图6  周向噪声与驱动转速的关系(1.025 kN·m)

Fig. 6  Relationship between circumference noise and driving speed

图7  径向噪声与负载的关系

Fig. 7  Relationship between radial direction noise and load resistance

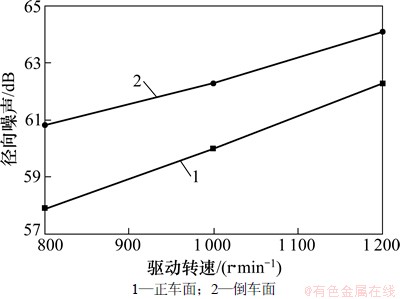
图8  径向噪声与驱动转速的关系(1.025 kN·m)

Fig. 8  Relationship between radial direction noise and driving speed

3  结论

(1) 摆线齿准双曲面齿轮在小轮的凹面驱动大轮的凸面的情况(正车)下，被动齿轮角速度的波动和角加速度的振动较稳定，噪声低，动态啮合性能和传动性能较好。

(2) 摆线齿准双曲面齿轮在空挡时动态啮合性能较差，对齿轮损害较大。

(3) 摆线齿准双曲面齿轮在同一转速下，随着阻力载荷的增加，噪声强度先增加后渐渐减少，主要是载荷越大，齿面变形越大，齿轮的重合度越高，啮合冲击减少，噪声强度降低。

参考文献：

[1] 侯旭明, 陈显勇, 刘素芬. 汽车螺旋锥齿轮失效分析[J]. 金属热处理, 2011, 36(2): 115-118.

HOU Xuming, CHEN Xianyong, LIU Sufen. Failure analysis on coach screw bevel gear[J]. Heat Treatment of Metal, 2011, 36(2): 115-118.

[2] Walha L, Fakhfakh T, Haddar M. Nonlinear dynamics of a two-stage gear system with mesh stiffness fluctuation, bearing flexibility and backlash[J]. Mechanism and Machine Theory, 2009, 44(5): 1058-1069.

[3] Ognjanovic M, Agemi F. Gear vibrations in supercritical mesh-frequency range caused by teeth impacts[J]. Journal of Mechanical Engineering, 2010, 56(10): 653-662.

[4] Kolivand M, Li S, Kahraman A. Prediction of mechanical gear mesh efficiency of hypoid gear pairs[J]. Mechanism and Machine Theory, 2010, 45(11): 1568-1582.

[5] Kahraman A, Singh R. Interactions between time-varying mesh stifness and clearance non-linearities in a geared system[J]. Journal of Sound and Vibration, 1991, 146(1): 135-156.

[6] 杨宏斌, 高建平, 方宗德, 等. 准双曲面齿轮非线性振动分析[J]. 汽车工程, 2000, 22(1): 51-54.

YANG Hongbing, GAO Jianping, FANG Zongde, et al. Non-linear dynamics of hypoid gears[J]. Automotive Engineering, 2000, 22(1): 51-54.

[7] FAN Yesen, WANG Sanmin, YANG Zhen, et al. Vibration analysis method for multi-rotor system geared by angular spiral bevel gears[J]. Journal of Harbin Institute of Technology, 2011, 43(3): 111-116.

[8] 王三民, 沈允文, 董海军. 含间隙和时变啮合刚度的弧齿锥齿轮传动系统非线性振动特性研究[J]. 机械工程学报, 2003, 39(2): 28-32.

WANG Sanmin, SHEN Yunwen, DONG Haijun. Nonlinear dynamical characteristics of a spiral bevel gear system with backlash and time-varying stiffness[J]. Chinese Journal of Mechanical Engineering, 2003, 39(2): 28-32.

[9] Cheng Y, Lim T C. Dynamics of hypoid gear transmission with nonlinear time-varying mesh characteristics[J]. Journal of Mechanical Design, 2003, 125(6): 373-382.

[10] 李军, 邢俊文, 覃文浩. ADAMS实例教程[M]. 北京: 北京理工大学出版社, 2002: 139-150.

LI Jun, XING Junwen, TAN Wenhao. ADAMS sample tutorials[M]. Beijing: Beijing Institute of Technology Press, 2002: 139-150.

[11] Ahn K Y, Ryu B J. A modeling of impact dynamics and its application to impact force prediction[J]. Proceedings of ACMD, 2004(2): 448-453.

[12] 谷口修. 振动工程大全: 下册[M]. 北京: 机械工业出版社, 1986: 582-583.

GU Kouxiu. Encyclopedia of vibration engineering: Lower volumes[M]. Beijing: China Machine Press, 1986: 582-583.

[13] 杨成云. 齿轮传动系统耦合振动响应及抗冲击性能研究[D]. 重庆: 重庆大学机械工程学院, 2006: 1-115.

YANG Chengyun. The research of the response of the coupled oscillations in the Gear transmission system and its impact resistance[D]. Chongqing: Chongqing University. College of Mechanical Engineering, 2006: 1-115.

(编辑  杨幼平)

收稿日期：2012-10-09；修回日期：2012-12-20

基金项目：国家自然科学基金资助项目(50975291)；教育部博士点基金资助项目(20120162110004)；国家重点基础研究发展计划(“973”计划)项目(2011-CB706800)

通信作者：严宏志(1964-)，男，湖南安乡人，博士，教授，博士生导师，从事数字化制造理论与技术研究；电话：0731 88876612；E mail：yhzcsu@163.com