精密运动平台宏微控制系统的设计
陈兴林,刘川,刘杨,张旭,王伟峰
(哈尔滨工业大学 航天学院,黑龙江 哈尔滨,150001)
摘要:基于高动态精密伺服运动双台系统模型提出一种非线性宏微控制方法。该方法采用长行程直线电机宏动跟随音圈电机高精密微动的驱动方式,并引入扩张状态观测器。系统在定位误差较大时,采用近似时间最优控制律的轻阻尼宏动台,以允许的最大速度快速响应,在接近目标位置后,再用采用复合非线性反馈控制律的重阻尼微动台来补偿宏动台超调引起的位置偏差,最终实现系统快速高精度的定位。通过扩张状态观测器观测系统的动态变化,补偿系统中的各种扰动,减小系统的稳态跟踪误差。研究结果表明:该方法改善系统的动态性能和抗干扰能力,提高系统的定位精度。
关键词:双台;直线电机;音圈电机;状态观测器;非线性
中图分类号:TP273+.3 文献标志码:A 文章编号:1672-7207(2013)06-2318-06
Dual-stage actuator control system design for precision motion platform
CHEN Xinglin, LIU Chuan, LIU Yang, ZHANG Xu, WANG Weifeng
(School of Astronautics, Harbin Institute of Technology, Harbin 150001, China)
Abstract: A nonlinear macro and micro control method for high dynamic precision servo dual-stage actuator (DSA) system was presented. An nm-level positioning precision is required by using macro movement of long stroke linear motor and high-precision micro movement of voice coil motor, and the introduction of extended state observer. When the position error of the system is large, the primary actuator controller is used to yield a closed-loop system with a small damping ratio for a fast rise time and certain allowable overshoot by the frame work of proximate time optimal control (PTOC). Then, a composite nonlinear feedback (CNF) control law was designed for the secondary actuator to reduce the overshoot caused by the primary actuator as the system output approaches the setpoint, and ultimately achieve the purpose of fast and high-precision positioning for the system. The extended state observer (ESO) was designed to estimate the unknown velocity and compensate the disturbance in servo systems, thus effectively removed the static error. The proposed control method was applied to an actual DSA positioning system. The experimental results demonstrate that our approach can improve the dynamic performance and the anti-jamming capability of the system, and enhance the control precision.
Key words: dual-stage actuator; linear motor; voice coil motor; state observer; nonlinear
高动态精密伺服运动平台是光刻机的重要部件。它要求在高速运动的情况下,采用长行程直线电机宏动跟随音圈电机高精密微动的驱动方式,在较短行程内实现对平台的精确定位。因此,直线电机作长行程宏动控制、磁力轴承及压电陶瓷等作微动精密补偿在国外一直是作为关键技术来研究和使用[1]。为了实现工件台大行程、高速、高精度的运动控制要求,控制系统须具有极高的动态响应和轨迹跟踪性能。近似时间最优控制(proximate time optimal control,PTOC)[2]是对TOC的改进,在系统误差较小时,采用线性控制律来代替原TOC基于开关函数的非线性控制律(Bang-bang控制律),实现对快速运动对象的准确定位。这种控制方法现已成功应用到硬盘磁头寻道伺服控制中,取得了较好的效果[3]。但是,PTOC线性工作区的控制律本质是比例控制,其性能具有常规PID的局限性,难以实现快速响应与低超调的矛盾[4]。Chen等[5]提出一种复合非线性反馈(composite nonlinear feedback,CNF)控制技术,通过动态改变闭环系统极点的阻尼,将轻阻尼系统的快速响应性能和重阻尼系统的低超调特性相结合,将CNF控制技术应用到硬盘的伺服控制系统中,实现了硬盘快速低超调的平稳定位。Zheng等在Chen的基础上,对CNF控制技术进行了改进,使控制时间减少[6],并将这种改进的方法应用到硬盘磁头定位控制中[7]。本文作者将PTOC控制律和CNF控制律相结合,采用直线电机宏动PTOC控制跟随音圈电机微动CNF控制的方式,并运用扩展状态观测器[8-10](extended state observer, ESO )对系统中的扰动进行补偿,以实现对系统快速平稳的定位,最后通过实验验证了该方法的有效性。
1 宏微运动控制系统模型
运动平台宏微运动控制系统的建模方式有很多 种[11-12],本文针对光刻机工件台控制系统,建立了宏微控制系统的等效模型,如图1所示。宏动台由直线电机驱动,气浮导轨导向;微动台由音圈电机驱动,由固定在宏动台上的气浮导轨导向;平衡质量块也是由气浮导轨导向,克服电机运动对基础框架的冲击。用光栅尺测量宏动台相对基础框架的位移yL,用激光干涉仪测量微动台相对基础框架的位移y;其中,宏动台的质量为M,微动台的质量为m;直线电机力输入为FL,音圈电机力输入为FS,宏动台与平衡质量块之间的阻尼与刚度分别为CL和KL,微动台与宏动台之间的阻尼与刚度分别为CS和KS,宏动和微动中的未知扰动量分别为dM和dm。

图1 宏微控制等效模型
Fig. 1 Illustration of a DSA model
在最后的实验验证中,因为实验台的M>>m和|(yL/yS)| >>1,忽略宏动和微动之间的耦合作用。
模型的动力学方程为:
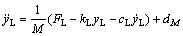 (1)
(1)
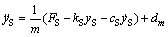 (2)
(2)
系统的状态方程为
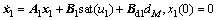 (3)
(3)
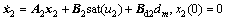 (4)
(4)
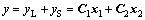 (5)
(5)
其中: ;
;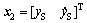 ;
;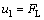 ;
;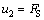 ;
;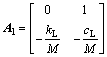 ;
;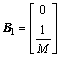 ;
;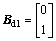 ;
;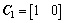 ;
;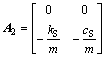 ;
;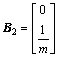 ;
;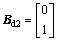 ;
;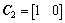 。
。
2 控制器设计
整个控制器分为3个部分:近似时间最优控制律(PTOC)、复合非线性反馈控制律(CNF)和各控制律所对应的扩张状态观测器(ESO)。宏动直线电机采用PTOC控制,微动音圈电机采用CNF控制,采用宏动跟踪微动的主从控制方式。控制结构如图2所示。
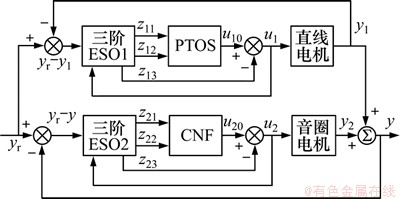
图2 控制结构框图
Fig. 2 Block diagram of control system
2.1 近似时间最优控制律
宏动系统为行程大、带宽小、精度较低的运动系统,采用近似时间最优控制律。近似时间最优控制(PTOC)在误差较大时,利用允许的最大控制信号来加速和减速,当误差较小时为线性控制,这样可以逼近TOC的性能,具有更好的鲁棒性。其控制律为:
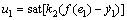 (6)
(6)
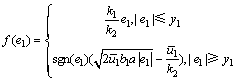 (7)
(7)
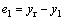 (8)
(8)
因为设定值yr为常数,所以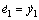 。
。
式中: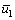 为u1的最大值;sat[·]为饱和函数;k1为位置反馈增益;k2为速度反馈增益;a(0<a<1)为加速度折扣系数;yl为线性区域的长度。为保证f(e1)连续,参数必须满足以下约束关系:
为u1的最大值;sat[·]为饱和函数;k1为位置反馈增益;k2为速度反馈增益;a(0<a<1)为加速度折扣系数;yl为线性区域的长度。为保证f(e1)连续,参数必须满足以下约束关系:
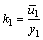 (9)
(9)
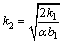 (10)
(10)
在区域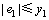 ,控制系统是线性的,运用文献[9]极点配置的方法,可得增益
,控制系统是线性的,运用文献[9]极点配置的方法,可得增益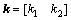 的值:
的值:
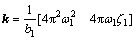 (11)
(11)
式中: 和
和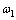 分别为闭环系统
分别为闭环系统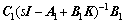 的阻尼比和自然频率,极点为:
的阻尼比和自然频率,极点为:
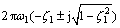 (12)
(12)
在以往双台的控制中,宏动系统都是采用增大宏动系统阻尼的方法,以减小运动系统的超调量。本文将选择较小的阻尼,使宏动系统快速的接近目标位置,再用微动系统来补偿掉这部分偏差,采用这种方法,可以减小控制时间。
2.2 复合非线性反馈控制律设计
微动控制系统,采用复合非线性反馈(CNF)控制。CNF控制律的核心思想[13]是通过动态改变闭环系统极点的阻尼,将轻阻尼系统的快速响应性能和重阻尼系统的低超调特性相结合,从而实现系统对目标位置快速平稳的定位与跟踪。CNF控制律设计分为两部分:一部分是常规的线性反馈控制律,用来保证微动闭环系统的稳定并使闭环系统具有较快的响应速度;另一部分是非线性反馈控制律,其作用随着系统输出接近目标值而变得越来越大,通过逐步增大闭环系统的阻尼从而抑制线性反馈部分造成的超调,最终的受控系统达到对设定点快速平稳的定位与跟踪,使输出y快速准确地定位到目标位置yr。
(1) 首先设计线性状态反馈控制律为:
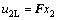 (13)
(13)
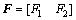 使系统
使系统 全局渐进稳定。
全局渐进稳定。
微动系统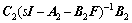 和宏动系统
和宏动系统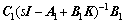 相比,阻尼比
相比,阻尼比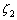 更大,自然频率
更大,自然频率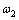 也更高。
也更高。
令
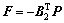 (14)
(14)
式中:P满足方程(15)。
求解Lyapunov方程
 (15)
(15)
式中:Q为正定对称矩阵,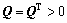 ;P为矩阵方程唯一的正定对称解,
;P为矩阵方程唯一的正定对称解,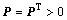 。
。
因为A2满足Hurwitz稳定判据,所以P存在。
为研究控制律的性质,定义
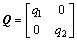 (16)
(16)
式中:q1和q2是可调整参数,q1>0,q2>0。将式(16)带入式(15)求出P,得
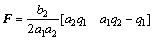 (17)
(17)
式中:a1=-(k2/m);a2=-(c2/m);b2=1/m;b1=1/M。
则闭环系统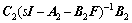 的阻尼比和自然频率分别为:
的阻尼比和自然频率分别为:
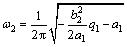 (18)
(18)
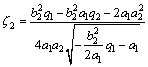 (19)
(19)
从式(18)和(19)可以看出:可以通过q1和q2来确定ω2和ζ2。
(2) 设计非线性反馈控制律为:
 (20)
(20)
式中:
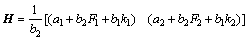 (21)
(21)
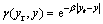 (22)
(22)
其中:H用来达到闭环系统期望的动态性能。β为非负的可调参数,γ(yr,y)的取值有界,为0≤γ(yr,y)≤1,其作用是随着y→yr,逐步增大闭环系统极点阻尼以减少超调。
将上面的非线性和线性结合在一起,CNF控制律为:
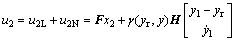 (23)
(23)
2.3 状态和扰动观测器的设计
考虑到实验系统为二阶控制系统,则应该用三阶扩张状态观测器[14]。最后实验是通过计算机来实现,则三阶线性ESO的离散表达式为:
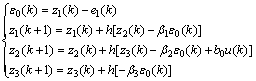 (24)
(24)
式中:h为步长;k为采样时刻;β1,β2和β3为扩张状态观测器的控制参数,决定了对e1(k)的估计情况和状态观测器的带宽。在图2中的ESO1,z11(k)和z12(k)分别为对误差e1(k)=yr-y1(k)和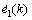 的估计,z13(k)为对未知扰动dM的估计补偿;在ESO2中,z21(k)和z22(k)分别为对误差e2(k)=yr-y(k)和
的估计,z13(k)为对未知扰动dM的估计补偿;在ESO2中,z21(k)和z22(k)分别为对误差e2(k)=yr-y(k)和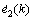 的估计,z23(k)为对未知扰动dm的估计补偿。
的估计,z23(k)为对未知扰动dm的估计补偿。
因宏动PTOC控制系统和微动CNF控制系统的带宽不一样,为准确的观测到系统状态,补偿系统扰动,所以ESO1和ESO2的带宽选择也不一样,一般选择观测器的带宽为ω0=(3~5)ωc。其中,ωc为相应控制系统的带宽;ω0为对应的扩张状态观测器的带宽。根据文献[15],β1,β2和β3和ω0的关系为:
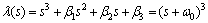 (25)
(25)
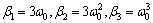 (26)
(26)
3 实验
实验系统如图3所示,精密运动平台的宏动电机采用线性无刷直线伺服电机BLMC-192-A,行程为200 mm;微动电机采用美国BEI Kimco公司的LA08-10-000A型直线音圈电机,行程为4 mm。运动控制器为自制版卡,采用TI公司的TMS320C6416型DSP芯片,主频1 GHz;宏动台的运动位置由HEIDENHAIN公司的LIP382光栅尺测得,其定位精度为±0.5 μm;微动台的运动位置由RENISHAW公司的XL-80激光干涉仪测得,其定位精度为±1 nm;系统采样周期为0.5 ms。M=10 kg,m=0.4 kg,cL=0,cS=0.000 8 N·s/m,kL=0,kS=0.4 N/m。
依据前面的对象模型,系统输出yL和yS单位为μm,则:
b1=1×105,a1=1×106,a2=-2 000,b2=2.6×106
选择参数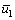 =100 N,ω1=20 Hz,ζ1=0.5,则yl=634 μm。
=100 N,ω1=20 Hz,ζ1=0.5,则yl=634 μm。
选择参数ω2=300 Hz,ζ2=0.9,则q1=0.817,q2=7.5×10-8。
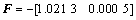 (27)
(27)
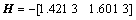 (28)
(28)
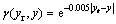 (29)
(29)
最后,进行2 mm和10 mm的定位实验。当选择yr=2 mm,y和yr之间的误差小于1 μm时,运行时间为48 ms,总位移y无超调,实验结果如图4所示;当yr=10 mm,y和yr之间的误差小于1 μm时,运行时间为96 ms,总位移y无超调,实验结果如图5所示。

图3 实验系统实物图
Fig. 3 Photograph of experimental system
通过采用相同的控制器和参数值,选择不同的目标位置yr,PTOC控制律和CNF控制律同时控制的双台都能很好的相互配合。当误差|e1|≥yl时,PTOC控制律发挥主要作用,使轻阻尼的宏动台快速响应,向目标位置迅速运动,减小台体与目标位置之间的误差;当误差|e1|≤yl时,PTOC控制律从非线性工作区域变换到线性工作区域,继续使误差逐渐减小,在误差逐渐减小的过程中,CNF控制律中的γ(yr,y)逐渐变大,CNF控制律开始发挥主要作用,采用CNF控制律的重阻尼微动台开始补偿掉宏动台所引起的超调,使系统误差减小到一定范围内,最后趋于稳定。在误差很小时,高带宽的微动台发挥主要作用,也使台体定位更加准确,稳定时间减小。由此可见,所设计的控制律具有较好的动态性能。
图6所示为系统无ESO时的系统稳态误差,最大的系统稳态误差为6 μm;图7所示为系统有ESO时的系统稳态误差,最大系统稳态误差0.9 μm。通过图6和图7 的对比发现有ESO的系统比没有ESO的系统稳态误差要小很多,这说明ESO对系统中的误差以及对误差的变化趋势都进行了很好的观测,对系统中的未知状态和未知扰动进行了估计,并对扰动进行了补偿,提高了系统的定位精度。
实验表明:采用宏动PTOC控制和微动CNF控制相结合的双台控制方式,再用ESO补偿该系统中的未知扰动和未建模动态,系统可以快速、准确、无超调地定位到目标位置,验证了该方法的有效性。
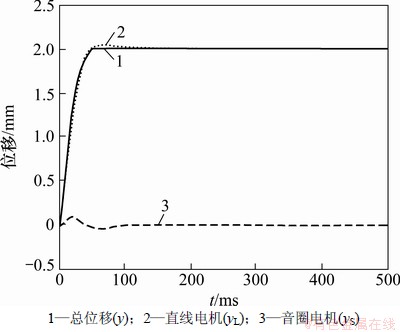
图4 2 mm双台运动曲线
Fig. 4 Dual-stage tracking control for 2 mm
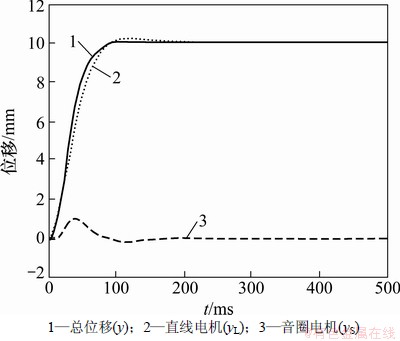
图5 10 mm双台运动曲线
Fig. 5 Dual-stage tracking control for 10 mm
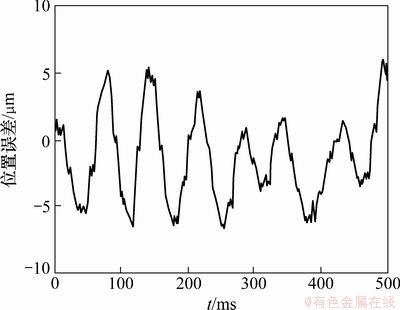
图6 无ESO的系统稳态位置误差
Fig. 6 Static position error without ESO
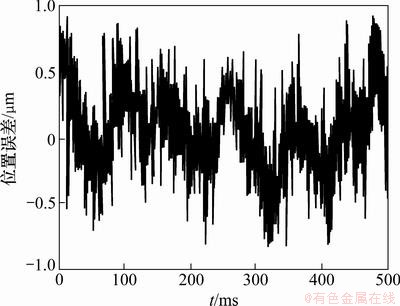
图7 有ESO的系统稳态位置误差
Fig. 7 Static position error with ESO
4 结论
(1) 将PTOC控制律和CNF控制律相结合,采用直线电机宏动PTOC控制跟随音圈电机微动CNF控制的方式,对双台进行控制,提高了系统的动态性能,减小了台体的稳定时间。
(2) 运用ESO对系统中的未知扰动和未建模动态进行补偿,改善了系统的抗干扰能力,提高了系统的定位精度。
(3) 控制器的设计采用全参数化表达式,方便调试和推广应用到其他的伺服控制系统。
参考文献:
[1] 刘丹, 陈兆宇. 步进扫描投影光刻机工件台和掩模台的进展[J]. 激光与光电子学进展, 2003, 40(5): 14-20.
LIU Dan, CHENG Zhaoyu. Process of wafer stage and reticle stage for step-and-scan-lithography system[J]. Laser & Optoelectronics Progress, 2003, 40(5): 14-20.
[2] Workman M, Adaptive proximate time-optimal servomechanisms[D]. Stanford, CA: Stanford University. Information Systems Laboratory, 1987: 24-25.
[3] Hredzak B, Herrmann G, Guo G. A proximate-time-optimal control design and its application to a hard disk drive dual-stage actuator system[J]. IEEE Transactions on Magnetics, 2006, 42(6): 1708-1715.
[4] 程国扬, 曾佳福. 快速定位伺服系统的控制器设计[J].电机与控制学报, 2009, 13(1): 52-56.
CHENG Guoyang, ZENG Jiafu. Controller design for fast servo positioning systems[J]. Electric Machines and Control, 2009, 13(1): 52-56.
[5] Chen B M, Lee T H, Peng K, et al. Composite nonlinear feedback control for linear systems with input saturation: Theory and an application[J]. IEEE Transactions on Automatic Control, 2003, 48(3): 427-439.
[6] Zheng J, Fu M. Nonlinear feedback control of a dual-stage actuator system for reduced setting time[J]. IEEE Transactions on Control Systems Technology, 2008, 16(4): 717-725.
[7] Zheng J, Fu M, Wang Y, et al. Nonlinear tracking control for a hard disk drive dual-stage actuator system[J]. IEEE/ASME Transactions on Mechatronics, 2008, 13(5): 510-518.
[8] Li S, Yang X, Yang D. Active disturbance rejection control for high pointing accuracy and rotation speed[J]. Automatica, 2009, 45: 1854-1860.
[9] 刘子建, 吴敏, 王一军. 基于自抗扰控制技术的高压大功率异步电机直接转矩控制系统[J]. 中南大学学报: 自然科学版, 2011, 42(11): 3392-3398.
LIU Zijian, WU Min, WANG Yijun. Direct torque control system of high-voltage high-power asynchronous machine based on active disturbance rejection control technique[J]. Journal of Central South University: Science and Technology, 2011, 42(11): 3392-3398.
[10] She J, Xin X, Pan Y. Equivalent-input-disturbance approach—Analysis and application to disturbance rejection in dual-stage feed drive control system[J]. IEEE/ASME Transactions on Mechatronics, 2011, 16(2): 330-340.
[11] 武志鹏, 陈兴林, 刘川. 光刻机工件台宏微系统的滑模变结构控制[J]. 光电工程, 2011, 38(9): 50-54.
WU Zhipeng, CHEN Xinglin, LIU Chuan. Sliding mode control of macro-micro system for wafer stage of lithography[J]. Opto-Electronic Engineering, 2011, 38(9): 50-54.
[12] 杨一博, 尹文生, 朱煜, 等. 粗精动超精密运动平台系统建模与分析研究[J]. 中国机械工程, 2008, 19(23): 2773-2776.
YANG Yibo, YIN Wensheng, ZHU Yu, et al. Modeling and analyzing for ultra-precision coarse-fine stage[J]. China Mechanical Engineering, 2008, 19(23): 2773-2776.
[13] 程国扬, 金文光. 硬盘磁头快速精确定位伺服控制系统的设计[J]. 中国电机工程学报, 2006, 26(12): 139-143.
CHENG Guoyang, JIN Wenguang. Design of a fast and precise head positioning servo control system for HDDS[J]. Proceedings of the CSEE, 2006, 26(12): 139-143.
[14] Han J. From PID to auto disturbances rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906.
[15] Gao Z. Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of the American Control Conference. Denver, Colorado, 2003: 4989-4996.
(编辑 杨幼平)
收稿日期:2012-06-07;修回日期:2012-09-14
基金项目:国家科技重大专项项目(2009ZX02207)
通信作者:刘川(1982-),男,四川资阳人,博士研究生,从事光刻机双工件台控制系统设计;电话:13946039547;E-mail:liuchuan1226@126.com