竖向刚度不规则高层框架结构推覆分析方法

黄群贤，郭子雄，杜培龙

(华侨大学 土木工程学院，福建 泉州，362021)

摘要：为研究侧向荷载模式和目标位移计算对不同类型竖向刚度不规则结构推覆分析结果的影响，建立竖向刚度不规则结构推覆分析方法。选择一栋12层的钢筋混凝土框架结构作为标准模型，通过对其刚度进行调整，建立4种常见的竖向刚度不规则形式的结构计算模型。采用5种固定侧向荷载模式和4种目标位移计算方法，分别对4种不同形式的竖向刚度不规则结构进行推覆分析，并与弹塑性时程分析结果进行比较分析。研究结果表明，在预测目标位移和层间位移上，侧向荷载模式和目标位移计算方法的选择对计算结果有较大影响，对不同的竖向刚度不规则结构应根据其不规则形式。给出竖向刚度不规则形式所对应的侧向荷载模式和目标位移计算方法合理选择表，其中侧向荷载模式三角分布ITR和能力谱方法(CapS)在计算竖向刚度不规则结构层位移和层间位移计算具有较好的通用性和实用性。研究成果可为竖向刚度不规则高层建筑结构抗震性能评估提供参考。

关键词：竖向刚度不规则；推覆分析；侧向荷载模式；目标位移；时程分析

中图分类号：TU311.3                文献标志码：A         文章编号：1672-7207(2014)11-3993-07

Pushover analysis of vertically stiffness-irregular high-rise building

HUANG Qunxian, GUO Zixiong, DU Peilong

(College of Civil Engineering, Huaqiao University, Quanzhou 362021, China)

Abstract: Pushover analysis of the vertically stiffness-irregular high-rise structures was established to investigate the influence of lateral-load mode and target-displacement calculation method on the calculated results of pushover analysis. A 12-storey RC frame was selected as the standard model, based on which the calculation models of four patterns of vertically stiffness-irregular structures were obtained by adjusting the stiffness. Pushover analysis was conducted by using five fixed lateral-load modes and four target-displacement calculation methods, and the calculated results were compared with elastic-plastic time history analysis. The results show that the selection of lateral-load mode and target-displacement calculation method significantly influences the predicting target-displacement and storey drift, and should be chosen according to irregular-pattern. The lateral-load mode with regard to vertically stiffness-irregular pattern and reasonable option list with regard to target-displacement calculation method can be obtained, and triangular distribution of lateral-load mode (ITR) and Capacity spectrum method (CapS) have better popularity and practicability in calculating storey drift. The results can be the reference for seismic estimation of vertically stiffness-irregular high-rise structures.

Key words：vertically irregular stiffness; pushover analysis; lateral load pattern; target displacement; step-by-step time history analysis

随着人们对建筑使用功能及体型要求的提高，越来越多的建筑在不同程度上呈现出结构不规则性，结构的不规则程度是影响结构抗震性能的重要因素之一。我国现行抗震规范明确要求对不规则且具有明显薄弱部位可能导致地震时严重破坏的建筑结构，应进行罕遇地震作用下的弹塑性变形分析。推覆分析方法是传统的静力弹塑性分析方法，其作为一种简单、快捷、有效的分析手段已经广泛应用于各种类型结构的研究。已有的研究成果表明^[1-6]，推覆分析方法在评估规则结构抗震性能评估中实际可行，但在不规则结构方面的应用尚缺少系统的研究^[7-11]。推覆分析结果的可靠性取决于2个重要因素：一是侧向力分布模式的合理选择，二是目标位移的准确计算。因此，要把推覆分析方法应用到不规则结构的弹塑性分析中，有必要对不规则结构的推覆分析方法的实用性进行系统研究。本文作者选择一栋12层钢筋混凝土框架规则结构，将其调整为4种常见的竖向刚度不规则形式的结构，选用较为常用的5种固定侧向荷载分布模式和4种目标位移计算方法，对竖向刚度不规则高层结构推覆分析方法在的适用性进行研究，通过与结构弹塑性动力时程分析结果的比较，给出不规则结构形式对应侧向荷载分布模式和目标位移计算方法的选择建议。

1  竖向刚度不规则框架计算模型

1.1  对比规则框架

对比结构为12层钢筋混凝土规则框架结构，层高均为3.3 m，其结构平面及竖向布置如图1所示。1~3层柱截面边长为550 mm，4~8层为500 mm，9~12层为450 mm。横向边跨梁截面长×宽为650 mm×250 mm，中跨梁截面长×宽为500 mm×250 mm，纵向框架梁截面长×宽为600 mm×300 mm。

本工程按7度进行抗震设防，场地类别为Ⅱ类，设计基本地震加速度为0.15 g，设计地震分组为第2组，场地特征周期为0.40 s。结构经PKPM程序TAT模块计算分析，得到梁柱配筋，所有梁柱截面纵向钢筋选用HRB335，箍筋为HPB235，各构件配筋率及强度等各项指标均满足规范要求。

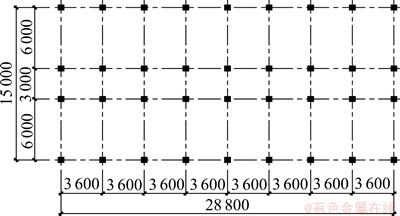
图1  规则框架平面布置图(单位：mm)

Fig. 1  Plane layout of regular frame

1.2  竖向刚度不规则框架计算模型

在进行竖向刚度不规则结构的推覆分析方法研究时，仅考虑刚度不规则在结构竖向的不同分布，不考虑强度不规则在结构竖向的影响。不规则与规则结构层刚度比如图2所示。

图2  不规则与规则结构层刚度比

Fig. 2  Storey-stiffness ratio between irregular and regular structures

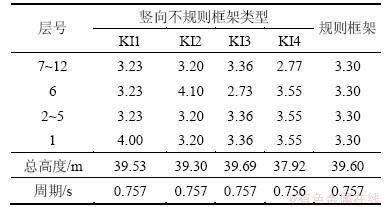
为使调整后的不规则框架与对比规则框架在抗震需求上具有可比性，须使2种框架具有相同的基本周期、质量和阻尼。因此，在调整刚度的过程中，不改变结构的材料，只对层高进行调整，并使其与对比框架的基本周期一致，且保持结构总高度基本不变。由于结构梁柱截面和材料性质没有改变，结构的总质量也基本保持不变。在进行竖向刚度不规则结构设计时，通过调整梁柱配筋，使结构的层间抗剪承载力与原结构一致。具体调整结果见表1。

表1  不规则框架层高及基本周期

Table 1  Storey height and fundamental period of irregular structures

2  不同侧向荷载模式推覆对比分析

2.1  侧向荷载模式

侧向荷载模式的选择是影响推覆分析方法对结构抗震性能的评估结果和其适用范围的重要因素之一。目前，国内外已提出了多种不同的侧向荷载模式，具体可分为固定荷载模式和适应性荷载模式2类。固定荷载模式在结构分析过程中荷载形状保持不变，而适应性荷载分布是一种可变荷载模式，其数值和形状与结构瞬时动力特性有关。适应性荷载模式能够反映高振型的影响，但计算繁琐，与推覆分析简化分析的思路相矛盾。故本文选用较为常用的5种固定侧向荷载分布模式进行研究：倒三角分布(ITR)、均布荷载分布(UNI)、指数分布(EXP)、模态分布(MODE)和与加速度成比例的分布模式(ACC)。

在对荷载模式进行评价时，主要进行层间位移需求预测和目标位移预测并与结构弹塑性动力时程(NLHA)计算结果比较。选用17条地震波对各不规则结构分别进行结构弹塑性动力时程分析，然后对各计算结果取平均值计算层位移和层间位移获得NLHA计算结果。分析所用地震波按照强度(幅值)、频谱特性和持时地震动进行选择和调整，并考虑了地震波频谱特性，因此所选17条地震波在统计意义上与规范的反应谱基本相符，如图3所示。所有不规则结构在通用结构分析软件SAP2000中建模并分析，在推覆分析中，统一采用能力谱方法(CapS)求解结构目标位移。

图3  加速度反应谱

Fig. 3  Acceleration response spectrum

2.2  层位移对比分析

图4所示为不规则结构的非线性动力时程分析结果与在5种侧向荷载模式作用下的推覆分析结果的层位移对比图。从图4可以看出：1) 在4种不规则形式中，5种荷载模式均能反映结构层位移沿竖向的变化规律，其中荷载模式ITR，EXP和MODE下预测的目标位移大于NLHA计算结果，而荷载模式UNI和ACC的目标位移预测结果小于NLHA分析结果。2) 荷载模式ITR和MODE对不规则形式KI1~KI3的层位移预测值与时程分析结果符合较好，其目标位移预测值和NLHA计算结果比值分别为1.05和1.02；3) 荷载模式UNI和ACC对不规则形式KI4的目标位移预测值与时程分析结果符合较好，其目标位移预测值和NLHA计算结果比值分别为0.99和0.98，具有较好的计算精度。

图4  不同侧向荷载模式下层位移计算结果

Fig. 4  Calculation results of storey drift under different lateral-load modes

2.3  层间位移对比分析

图5所示为刚度不规则结构的非线性动力时程分析结果与在5种侧向荷载模式作用下的推覆分析结果的层间位移对比图。从图5可以看出：1) 除了荷载模式EXP在不规则形式KI1中预测结构薄弱层的位置与NLHA分析结果不符外，ITR，MODE和EXP 3种荷载模式在各规则形式中均能较好地预测结构薄弱层的位置，但在最大层间位移的数值预测上，推覆分析结果大于NLHA分析结果，需对最大层间位移进行修正；2) 荷载模式UNI和ACC在4种刚度不规则形式中在预测结构薄弱层的位置上与NLHA分析结果不符。

2.4  竖向不规则结构的合理侧向荷载模式

12层竖向不规则框架结构的合理侧向荷载模式选择如表2所示。从表2可以看出，多种不规则结构类型采用推覆分析方法预测目标位移和层间位移需求时，其较为合适的荷载模式并不统一。因此，为了使目标位移预测值和层位移需求预测值更接近时程分析结果，分别采用不同的侧向荷载模式更为合理。此外，在层位移和层间位移计算中，侧向荷载模式ITR在各不规则结构中具有较好的适用性。

表2  12层不规则结构推覆分析侧向荷载模式选择

Table 2  Lateral load patterns of pushover analysis for vertically stiffness-irregular 12-storey structures

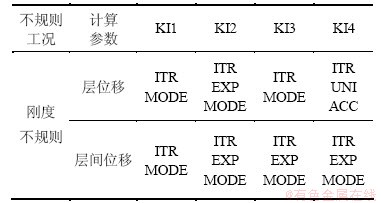
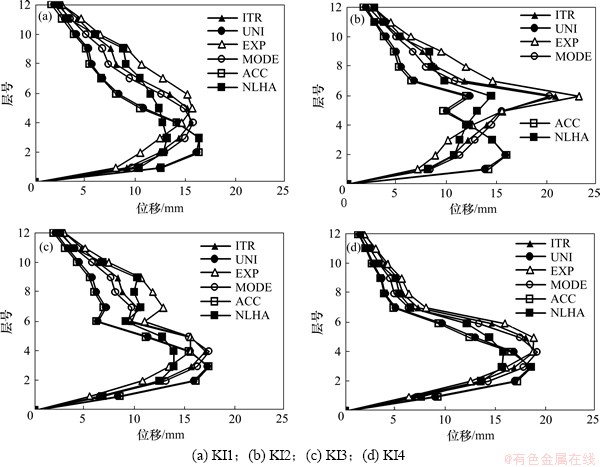
图5  不同侧向荷载模式下层间位移计算结果

Fig. 5  Calculation results of inter-storey drift under different lateral-load modes

3  不同目标位移计算方法对比分析

3.1  目标位移计算方法

为研究不同的目标位移计算方法对竖向不规则结构推覆分析结果的影响，将分别采用等效位移系数法(EDCM)、能力谱方法(CapS)、等效单自由度体系法(ESDOF)和目标位移计算改进方法^[3](IMP)等4种方法进行目标位移计算。根据计算的目标位移进行结构推覆分析，与结构非线性动力时程分析(NLHA)结果的比较，研究推覆分析采用不同的目标位移计算方法对于竖向不规则结构抗震性能评估的影响，并根据其不规则形式给出建议的目标位移计算方法。对不规则结构进行推覆分析所采用的侧向荷载模式根据表2选取。在对目标位移计算方法进行评价时，主要考察层位移和层间位移在抗震需求预测上的准确程度。

3.2  层位移对比分析

图6所示为12层刚度不规则结构的非线性动力时程分析与在4种目标位移计算方法下的推覆分析层位移对比图。从图6可以看出：1) 在4种刚度不规则结构形式的推覆分析中，EDCM与ESDOF方法在目标位移预测上与NLHA分析结果相比误差较大，其中EDCM方法在目标位移预测大于NLHA分析结果，而ESDOF方法在目标位移预测小于NLHA分析结果。采用2种方法进行目标位移计算需对计算结果进行修正，修正系数可分别取0.72和1.35。2) CapS方法在目标位移预测与NLHA分析结果符合较好，是合理的预测方法。3) IMP方法是在ESDOF方法的基础上考虑了高振型的影响，在4种刚度不规则形式的分析中，IMP方法在预测目标位移上比ESDOF方法具有更好的精度，说明在高层刚度不规则结构的目标位移计算中，高振型的影响不可忽略。其中对于KI2和KI3，IMP方法在目标位移预测具有较高的精度，相对误差在10%以内。

3.3  层间位移对比分析

图7所示为刚度不规则12层结构的非线性动力时程分析与在4种目标位移计算方法下的推覆分析层间位移对比图。从图7可以看出：1) 在推覆分析中，由于荷载模式按照表2选取，因此4种方法在层间位移预测值沿竖向的分布均能反映NLHA分析结果在层间位移的分布规律；2) ESDOF方法在层间位移预测值最小，而EDCM方法在层间位移预测值最大；3) 在不规则结构形式KI1，KI3和KI4，CapS方法的层间位移预测值接近于NLHA分析结果具有较高的精度，而ESDOF方法的层间位移预测值与NLHA分析结果符合较好。4) 在最大层间位移角的预测上，CapS方法与NLHA分析结果最接近，采用该方法预测最大层间位移角需对计算结果进行修正，修正系数可取0.8。

图6  不同目标位移计算方法的层位移计算结果

Fig. 6  Calculation results of storey drift under different target-displacement calculation methods

3.4  竖向不规则结构的合理的目标位移计算方法

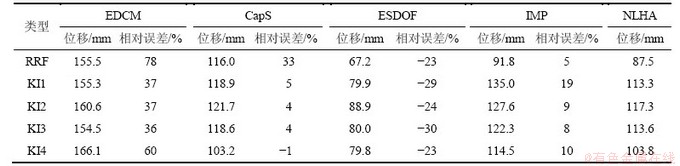
在选定的荷载模式下，按4种目标位移计算方法计算的目标位移进行推覆分析，4种目标位移计算方法的目标位移预测值和层间位移预测值相差较大，均能够探测到结构薄弱层的位置。表3所示为各计算方法在各规则和不规则结构中的目标位移预测值及其与时程分析结果的误差。从表3可以看出：按等效位移系数法(EDCM)计算的目标位移进行推覆分析，层位移预测值和层间位移预测值大于时程分析结果，等效单自由度体系法(ESDOF)的目标位移预测值最小，二者误差均较大。而按等效单自由度体系改进方法(IMP)和能力谱方法(CapS)计算的目标位移，在绝大多数情况下和非线性时程分析(NLHA)结果接近，说明改进方法和能力谱方法在竖向不规则结构中有较好的实用性。

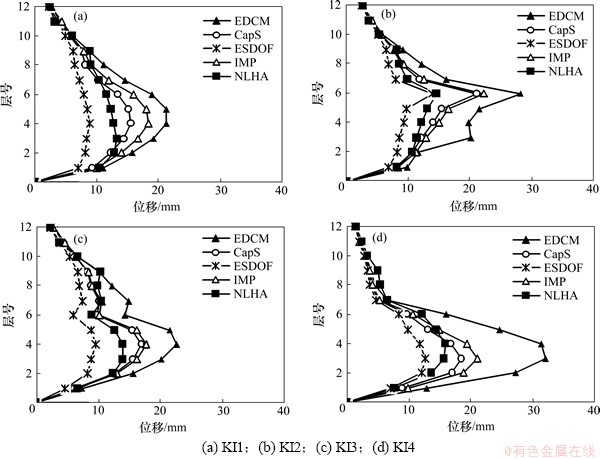
图7  不同目标位移计算方法的层间位移计算结果

Fig. 7  Calculation results of inter-storey drift under different target-displacement calculation methods

表3  不同目标位移计算方法与时程分析结果的比较

Table 3  Comparison between results of different methods and time history method

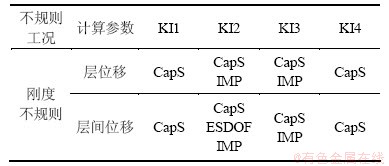
对于12层不规则结构，用推覆分析来评估结构抗震性能时采用的较合适的目标位移计算方法如表4所示。从表4可以看出：能力谱方法(CapS)在计算竖向刚度不规则结构目标位移具有较好的通用性和实用性。

表4  12层不规则框架结构目标位移计算方法选择

Table 4  Calculation method of target displacement for irregular 12-storey frame structures

4  结论

1) 多种不规则结构类型采用推覆分析方法预测目标位移和层间位移时，其较为合适的荷载模式并不统一，为了使目标位移预测值和层位移预测值更接近时程分析结果，分别采用不同的侧向荷载模式更为合理。

2) 在选定的荷载模式下，4种目标位移计算方法的目标位移预测值和层间位移预测值相差较大，但均能够探测到结构薄弱层的位置。

3) 在4种不规则形式中，各目标位移计算方法的目标位移计算结果相差较大。能力谱方法CapS和改进方法IMP的目标位移预测值较接近NLHA分析结果，相对误差较小，实用性较强。

4) 给出竖向刚度不规则形式所对应的侧向荷载模式和目标位移计算方法合理选择表。在各竖向不规则结构推覆分析中，侧向荷载模式ITR和能力谱方法(CapS)在计算结构层位移和层间位移计算具有较好的通用性和实用性。研究成果可为推覆分析在竖向不规则结构的应用提供依据。

参考文献：

[1] 郭子雄. 基于变形的抗震设计理论及应用研究[D]. 上海: 同济大学土木工程学院, 2000: 10-55.

GUO Zixiong. Study on deformation-based seismic design theory with application[D]. Shanghai: Tongji University. School of Civil Engineering, 2000: 10-55.

[2] 杜培龙. 竖向不规则结构弹塑性地震反应简化分析方法的研究[D]. 泉州: 华侨大学土木工程学院, 2005: 10-75.

DU Peilong. Study on simplified analysis method of nonlinear seismic response of structures with vertical irregularity[D]. Quanzhou: Huaqiao University. School of Civil Engineering, 2005: 10-75.

[3] 吴毅彬, 杜培龙, 郭子雄. 一种改进的结构推覆分析目标位移计算方法[J]. 华侨大学学报(自然科学版), 2007, 28(2): 188-191.

WU Yibin, DU Peilong, GUO Zixiong. An improved method for calculating the target displacement of pushover analysis[J]. Journal of Huaqiao University (Natural Science), 2007, 28(2): 188-191.

[4] 沈蒲生, 龚胡广. 多模态静力推覆分析及其在高层混合结构体系抗震评估中的应用[J]. 工程力学, 2006, 23(8): 69-74.

SHEN Pusheng, GONG Huguang. Multi-mode pushover analysis and seismic evaluation in hybrid structures[J]. Engineering Mechanics, 2006, 23(8): 69-74.

[5] Chintanapakdee C, Chopra A K. Seismic response of vertically irregular frames: response history and modal pushover analyses[J]. Journal of Structural Engineering, 2004, 130(8): 1177-1185.

[6] Mwafy A A, Elnashai A S. Static pushover versus dynamic collapse analysis of RC frames[J]. Engineering Structures, 2001, 23(5): 407-424.

[7] 门进杰, 史庆轩, 周琦. 平面不规则混凝土框架结构非线性静力分析侧向力计算方法的研究[J]. 世界地震工程, 2007, 23(1): 125-129.

MEN Jinjie, SHI Qingxuan, ZHOU Qi. Research on lateral load distribution method for asymmetric frame structures in nonlinear static analysis[J]. World Earthquake Engineering 2007, 23(1): 125-129.

[8] Kunnath S K. Identification of modal combinations for nonlinear static analysis of building structures[J]. Computer-aided Civil and Infrastructure Engineering, 2004, 19(4): 246-259.

[9] Kalkan E, Kunnath S K. Adaptive modal combination procedure for nonlinear static analysis of building structures[J]. Journal of Structural Engineering, 2006, 132(11): 1721-1731.

[10] Kalkan E, Kunnath S K. Lateral load distribution in nonlinear static procedures for seismic design[C]// Proceedings of the 2004 Structures Congress. Nashville, Tennessee, 2004: 22-26.

[11] Chopra A K, Goel R K. A modal pushover analysis procedure for estimating seismic demands for buildings[J]. Earthquake Engineering and Structural Dynamics, 2002, 31(3): 561-582.

(编辑  赵俊)

收稿日期：2013-11-16；修回日期：2014-02-10

基金项目(Foundation item)：国家自然科学基金资助项目(51208219)；福建省科技计划重点项目(2012Y0051)；厦门科技计划重点项目(3502Z20123033) (Project(51208219) supported by the National Natural Science Foundation of China; Project(2012Y0051) supported by the Important Science and Technology Program of Fujian Province, China; Project(3502Z20123033) supported by the Important Science and Technology Program of Xiamen, China)

通信作者：黄群贤(1977-)，男，福建泉州人，博士，副教授，从事工程结构抗震与防灾方向研究；电话：0595-22691787；E-mail: huangqx@hqu.edu.cn