J. Cent. South Univ. Technol. (2010) 17: 1285-1292
DOI: 10.1007/s11771-010-0633-y
Dynamic matrix encoding strategy for voice-over-IP steganography
TIAN Hui(田晖)1, 2, ZHOU Ke(周可)1, 2, FENG Dan(冯丹)1, 2
1. Wuhan National Laboratory for Optoelectronics, Huazhong University of Science and Technology,
Wuhan 430074, China
2. School of Computer Science and Technology, Huazhong University of Science and Technology,
Wuhan 430074, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2010
Abstract: In order to optionally regulate embedding capacity and embedding transparency according to user’s requirements in voice-over-IP (VoIP) steganography, a dynamic matrix encoding strategy (DMES) was presented. Differing from the traditional matrix encoding strategy, DMES dynamically chose the size of each message group in a given set of adoptable message sizes. The appearance possibilities of all adoptable sizes were set in accordance with the desired embedding performance (embedding rate or bit-change rate). Accordingly, a searching algorithm that could provide an optimal combination of appearance possibilities was proposed. Furthermore, the roulette wheel algorithm was employed to determine the size of each message group according to the optimal combination of appearance possibilities. The effectiveness of DMES was evaluated in StegVoIP, which is a typical covert communication system based on VoIP. The experimental results demonstrate that DMES can adjust embedding capacity and embedding transparency effectively and flexibly, and achieve the desired embedding performance in any case. For the desired embedding rate, the average errors are not more than 0.000 8, and the standard deviations are not more than 0.002 0; for the desired bit-change rate, the average errors are not more than 0.001 4, and the standard deviations are not more than 0.002 6.
Key words: steganography; embedding transparency; dynamic matrix encoding strategy; voice over IP
Introduction
Steganography, an art and science of information hiding, has attracted increasing interest. However, most of existing studies on steganography are carried out on storage media (e.g., image [1], video [2], audio [3], text [4]) and, by contrast, the area of steganography over streaming media is largely unexplored. However, as a nice steganographic cover, streaming media can potentially offer better security for hiding covert messages by virtue of its instantaneity, because it does not give eavesdroppers sufficient amount of time to detect possible abnormity due to hidden messages. In fact, the recognition of specific streaming media in enormous network traffic is a very perplexing and challenging problem, letting alone detecting possible covert messages. In this work, voice-over-IP (VoIP), a typical streaming medium, was chosen as a possible carrier to apply steganography.
VoIP is a promising technique to enable telephone calls via a broadband Internet connection. Owing to the advantages of low cost and flexible advanced digital features, VoIP became a popular alternative to the public-switched telephone network (PSTN), and extensive research on it was conducted [5]. In recent years, many researchers have carried out useful research on steganography over VoIP, such as prototype implementations of steganography over VoIP [6-10], a lossless steganography method for μ-law of G 711 [11], a steganography method named LACK using the lost VoIP packets [12], an adaptive steganography method using partial similarity [13], an m-sequence based steganography model [14], and a codebook partition based steganography method [15]. Differing from the previous studies, encoding strategies used to enhance the embedding performance were investigated in this work.
Generally, the key criteria for steganography are perfect transparency for non-authenticated entities and high capacity for carrying secret messages. The first criterion, a measure of embedding distortion, is often more important. An acknowledged belief is that the smaller the embedding distortion, the harder the detection of the embedding changes. Therefore, many effective methods to enhance the transparency were developed. For example, the random interval method (RIM) improves the steganographic transparency by spreading the secret message over the cover in a random manner [16]; the random position method (RPM), on the other hand, dynamically determines substitution bits with given probability thresholds [17]. Both of them can decrease the amount of substitution bits and reduce the distortion. In addition, TSENG et al [18] presented a secure data hiding approach for binary images, which can conceal bits of data in a binary image block of size m×n by modifying at most two bits. Matrix encoding strategy (MES) is another general principle that can be applied to most steganographic schemes to improve their transparency. MES was first introduced by CRANDALL [19] and was made popular by Westfeld [20] who incorporated a specific implementation using binary Hamming codes in his F5 algorithm. Although FRIDRICH and SOUKAL [21], and KHATIRINEJAD and LISON?K [22] further extended MES from Hamming codes into many other linear codes, MES based on Hamming codes offers the best steganographic transparency, which can embed r bits into 2r-1 cover bits with no more than one bit changed. Thus, MES based on Hamming codes is often considered as the standard MES. However, in MES, the embedding capacity and the embedding transparency largely depend on the fixed size of message groups and cannot be regulated optionally. Therefore, MES cannot totally satisfy the requirements of the steganography based on VoIP. In fact, since the VoIP-based steganography is often used to construct covert communication, it is significant to flexibly regulate the embedding capacity and the embedding transparency, and strike an acceptable balance between them according to different requirements of users.
bits of data in a binary image block of size m×n by modifying at most two bits. Matrix encoding strategy (MES) is another general principle that can be applied to most steganographic schemes to improve their transparency. MES was first introduced by CRANDALL [19] and was made popular by Westfeld [20] who incorporated a specific implementation using binary Hamming codes in his F5 algorithm. Although FRIDRICH and SOUKAL [21], and KHATIRINEJAD and LISON?K [22] further extended MES from Hamming codes into many other linear codes, MES based on Hamming codes offers the best steganographic transparency, which can embed r bits into 2r-1 cover bits with no more than one bit changed. Thus, MES based on Hamming codes is often considered as the standard MES. However, in MES, the embedding capacity and the embedding transparency largely depend on the fixed size of message groups and cannot be regulated optionally. Therefore, MES cannot totally satisfy the requirements of the steganography based on VoIP. In fact, since the VoIP-based steganography is often used to construct covert communication, it is significant to flexibly regulate the embedding capacity and the embedding transparency, and strike an acceptable balance between them according to different requirements of users.
In this work, a dynamic matrix encoding strategy for the VoIP-based steganography was proposed to achieve the desired steganographic performance by flexibly adjusting the embedding transparency and the embedding capacity.
2 Steganography based on VoIP
Fig.1 depicts a general steganographic scheme in the VoIP scenario. Assume Alice (the sender) wants to transmit secret message to Bob (the receiver), while they are talking about some inconspicuous topics via the VoIP system. For that, Alice embeds the secret message into the VoIP stream with an embedding algorithm; after the VoIP stream is sent through the channel, Bob retrieves the secret message with the corresponding restituting algorithm.
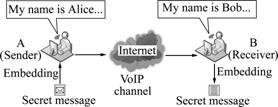
Fig.1 Steganography in VoIP scenario
Generally, a given steganographic scheme is believed to possess an inherent steganographic performance. However, recent investigation shows that proper encoding strategies can further enhance the steganographic performance, which is the motivation to present a dynamic matrix encoding strategy (DMES) in this work. For ease of presentation, the well-known least- significant-bits (LSBs) steganographic scheme is typically taken as an example, although the proposed strategy is also applicable to various steganographic schemes.
3 Matrix encoding strategy
As the foundation of DMES, this section briefly introduces the standard MES based on Hamming codes in VoIP-based scenarios. Assume that M={m1, m2, …, mQ} is the bit set of a given secret message (it may be encrypted beforehand, which is irrelevant in this work), where Q is the length of the secret message; C={c1, c2, …, cL} is the LSBs set in the VoIP stream and the embedding result is denoted by  …,
…,  where L is the total number of LSBs. In a real-time application, the “divide and rule” strategy is often adopted. In other words, M and C are divided into N and S parts, respectively, i.e., M={M′1, M′2, …, M′N} and C= {C′1, C′2, …, C′S}, where M′i={m′i1, m′i2, …, m′ir}, C′i= {c′i1, c′i2, …, c′il}, l=2r-1, Q=N×r, and L=S×l. Apparently, the matrix size depends on the size of message group r, which needs to be shared between both the communicating parties. It is usually assumed that the size of message groups is chosen beforehand and communicated over a secure channel prior to starting the covert communication. However, a real-time synchronization mechanism in Ref.[16] can also be employed as another feasible solution for this problem.
where L is the total number of LSBs. In a real-time application, the “divide and rule” strategy is often adopted. In other words, M and C are divided into N and S parts, respectively, i.e., M={M′1, M′2, …, M′N} and C= {C′1, C′2, …, C′S}, where M′i={m′i1, m′i2, …, m′ir}, C′i= {c′i1, c′i2, …, c′il}, l=2r-1, Q=N×r, and L=S×l. Apparently, the matrix size depends on the size of message group r, which needs to be shared between both the communicating parties. It is usually assumed that the size of message groups is chosen beforehand and communicated over a secure channel prior to starting the covert communication. However, a real-time synchronization mechanism in Ref.[16] can also be employed as another feasible solution for this problem.
Generally, for a given message group and the corresponding LSBs group
and the corresponding LSBs group MES involves the following steps.
MES involves the following steps.
Step 1: Assign the dependencies with the binary coding of i to c′i; regard each binary coding as a column vector Bi=(bi1, bi2, ?, bir)T, where

where bij=0 or 1.
Encoding matrix A consists of all these vectors, i.e.
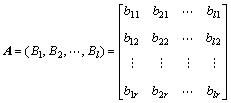

Step 2: For each row in A, calculate

where 1≤j≤r;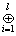 represents continuous XOR operations.
represents continuous XOR operations.
Step 3: Calculate the following expression:

If X=0, there are no bits needed to be modified in C′; otherwise, the Xth bit c′X needs to be flipped, namely, 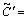 {c′1, c′2, ?, 1-c′X , ?, c′l}.
{c′1, c′2, ?, 1-c′X , ?, c′l}.
The following example concretely shows the steps. Assume that r = 3, l =7, M′ ={0, 0, 1} and C′ ={0, 1, 1, 0, 0, 1, 1}. According to step 1, the encoding matrix is

Further, according to Eq.(3), we can obtain x1=0, x2=0, x3=1. Due to X=0×1+0×2+1×4=4, c′4 needs to be flipped, namely,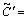 {0, 1, 1, 1, 0, 1, 1}.
{0, 1, 1, 1, 0, 1, 1}.
The restituting approach is very simple. The receiver first extracts  from the VoIP stream and obtains each bit of embedded message by calculating the following expression:
from the VoIP stream and obtains each bit of embedded message by calculating the following expression:
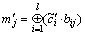
where 1≤j≤r.
For the given example, it is easy to restitute m′1=0, m′2=0 and m′3=1, namely M′={0, 0, 1}.
For each LSBs group, the embedding rate (denoted by W(r)) can be calculated as follows:
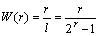
Essentially, W(r) indicates the average number that can be embedded per cover bit, which is often used to evaluate the embedding capacity of a given approach.
Moreover, the average distortion (i.e., the average number of changed bits, denoted by S(r)) for each LSBs group can be calculated as follows:

Accordingly, the bit-change rate (denoted by D(r)) can be calculated as follows:
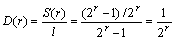
D(r) that indicates the change density (i.e., the average number of bits changed per cover bit) is often employed to evaluate the embedding transparency. To synthetically evaluate the embedding performance, we can further define the embedding efficiency (denoted by E(r)), which indicates the average number of bits that can be embedded per bit-change of the cover, namely,
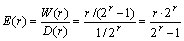
Table 1 lists the concrete performances for different values of r. From these data, it can be learnt that: (1) E(r) is always larger than the size of message groups, namely, E(r)>r; (2) S(r) increases with the increase of r, although it is always not larger than 1.0; (3) D(r) decreases with the decrease of W(r), which indicates that MES enhances the embedding transparency at the cost of a decreased W(r); and (4) W(r) and D(r) are determined by the given fixed size of message groups, so they cannot be regulated optionally.
Table 1 Embedding performances of MES

4 Dynamic matrix encoding strategy (DMES)
As an improved MES, DMES can flexibly regulate W(r) and D(r) by dynamically determining the size of each message group. That is, DMES divides the whole message into many parts with different sizes rather than a single fixed size to achieve the dynamic adjustment of W(r) and D(r). Assume that, DMES adopts n different message group sizes, denoted by set R={r1, r2, …, rn}, where ri<ri+1, i=1, 2, …, n-1, and their corresponding appearance probabilities P={p1, p2, …, pn}, then the following equations can be obtained:


where α and β are desired W(r) and D(r), respectively, 
 and
and  P, pi
P, pi [0, 1]. The above formal description indicates that DMES is essentially a multi-objective optimization problem, which aims at optimizing all pi
[0, 1]. The above formal description indicates that DMES is essentially a multi-objective optimization problem, which aims at optimizing all pi P simultaneously. Apparently, the complexity of this problem increases with the increase of the number of the adopted different message group sizes, i.e., n. Fortunately, in practical applications, it is unnecessary to involve too many different message group sizes. Typically, R1={1, 2, 3} or R2={2, 3, 4} can be chosen as the set of optional message group sizes (their sufficiency to get desired α and β will be presented later). For sets R1 and R2, Eq.(10) can be converted into,
P simultaneously. Apparently, the complexity of this problem increases with the increase of the number of the adopted different message group sizes, i.e., n. Fortunately, in practical applications, it is unnecessary to involve too many different message group sizes. Typically, R1={1, 2, 3} or R2={2, 3, 4} can be chosen as the set of optional message group sizes (their sufficiency to get desired α and β will be presented later). For sets R1 and R2, Eq.(10) can be converted into,


where p1, p2 and p3 [0, 1]; for set R1, α
[0, 1]; for set R1, α [0.428 6, 1.000 0], β
[0.428 6, 1.000 0], β [0.125 0, 0.500 0] and λ=0; for set R2, α
[0.125 0, 0.500 0] and λ=0; for set R2, α [0.266 7, 0.666 7], β
[0.266 7, 0.666 7], β [0.062 5, 0.250 0] and λ=1.
[0.062 5, 0.250 0] and λ=1.
Seemingly, p1, p2 and p3 can be simply obtained according to given α and β by solving the system of equations. However, it is actually not true. It is not hard to find a counterexample, for example, if set R2 is adopted, α=0.500 0, and β=0.250 0, by solving Eq.(11), p1=2.409 1, p2=-2.045 5 and p3=0.636 4 can be obtained, but these values are apparently invalid for p1, p2 and p3 [0, 1]. In fact, there is a certain relationship between α and β. To determine this relationship, algorithm 1 was employed to search for all possible combinations of α and β.
[0, 1]. In fact, there is a certain relationship between α and β. To determine this relationship, algorithm 1 was employed to search for all possible combinations of α and β.
Algorithm 1 Searching algorithm of combination of α and β
Require: step is a constant that denotes the search step: A[ ] and B[ ] are arrays used to store valid α and β, respectively.
1: p1=0;
2: count=0;
3: while (pl≤1.0);
4: p2=0;
5: while (p2≤1.0);
6: p3=1.0-p1-p2;
7: if (0≤p3≤1.0) then
8: Calculate α and β according to formula (10);
9: A[count]=α;
10: B[count]=β;
11: count=count+1;
12: end if
13: p2=p2+step;
14: end while
15: p1=p1+step;
16: end while
Fig.2 shows the relationship of α and β under different parameter settings. From Fig.2, it can be seen that the desired α [0.266 7, 1.000 0] or β
[0.266 7, 1.000 0] or β [0.062 5, 0.500 0] can be obtained by properly setting p1, p2 and p3 using sets R1 or R2. In other words, sets R1 and R2 are sufficient to be employed to obtain the desired α or β. Furthermore, for a given value of α (or β), there are a set of corresponding values of p1, p2 and p3. To achieve the best embedding performance, algorithm 2 was used to obtain the optimal combination of p1, p2 and p3.
[0.062 5, 0.500 0] can be obtained by properly setting p1, p2 and p3 using sets R1 or R2. In other words, sets R1 and R2 are sufficient to be employed to obtain the desired α or β. Furthermore, for a given value of α (or β), there are a set of corresponding values of p1, p2 and p3. To achieve the best embedding performance, algorithm 2 was used to obtain the optimal combination of p1, p2 and p3.

Fig.2 Relationship between α and β: (a) Using set R1 and step=0.01; (b) Using set R2 and step=0.01
Algorithm 2 Searching algorithm of optimal p1, p2 and p3
Require: step is a constant that denotes the search step; α0 and β0 are the desired W(r) and D(r); err is the allowable error for the major concern (α0 or β0); A[ ], B[ ] and C[ ] are arrays used to respectively store valid α, β and α/β; P1[ ], and P2[ ] and P3[ ] are arrays used to respectively store selectable p1, p2 and p3.
Output: p1*, p2* and p3*, which are the respectively optimal values of p1, p2 and p3; α* and β*, which are respectively the practical W(r) and D(r).
1: k=0; p1=0;
2: while (p1≤1.0)
3: p2=0;
4: while (p2≤1.0)
5: p3=1.0-p1-p2;
6: if (0≤p3≤1.0) then
7: Calculate α and β according to Formula (10);
8: if (α==α0) then
9: α*=α; β*=β;
10: p1*= p1, p2*=p2; p3*=p3;
11: return;
12: else if (|α-α0|≤err) then
13: A[k]=α; B[k]=β; C[k]=α/β;
14: P1[k]=p1; P2[k]=p1; P3[k]=p3;
15: k=k+1;
16: end if
17: end if
18: p2=p2+step;
19: end while
20: p1=p1+step;
21: end while
22: i=0; γ=C[0]; opt=0;
23: while (i<k)
24: if (γ>C[i]) then
25: γ=C[i]); opt=i;
26: end if
27: end while
28: p1*=P1[opt]; p2*=P2[opt]; p3*=P3[opt];
29: α*=A[opt]; β*=B[opt]
The main idea of algorithm 2 is as follows: (1) search for the desired values of p1, p2 and p3 according to the major concern (W(r) is taken for an example here, and D(r) can also be chosen); (2) if no combination of p1, p2 and p3 can achieve the exact value of the major concern, choose the optimal combination among all candidates, which can achieve an approximate value of the major concern in the range of allowable error and the maximum embedding efficiency. It is worth noting that the search process is often carried out offline, and a datasheet is made accordingly, in which the optimal combination of p1, p2 and p3 can be looked up anytime.
Another significant problem is that synchronization between the sender and the receiver should be exactly achieved. Generally, the synchronization problem of DMES consists of two parts: (1) the negotiation of adopted parameters, namely, p1, p2 and p3; and (2) the approach for the receiver to exactly know the subsections of the embedded message adopted by the sender. For the first part, the approach adopted in the traditional MES is also applicable. However, there are no ready-made answers for the second part. A straightforward method is that the sender transmits the size of each message group to the receiver beforehand. Unfortunately, the sender cannot exactly determine the length of the embedded message beforehand, not to mention the sizes of all message groups, because the length of the cover speech that depends on the conversation is often unpredictable. To solve this problem, the “roulette wheel algorithm” was introduced to determine the size of each message group. The detailed process can be stated as follows: generate a pseudo random number (PRN) p [0, 1] using a uniform generator (e.g., Mersenne twister [23]); if p≤p1, set the current size (denoted by r) as r1 in set R1 (or R2), namely, r=r1; if p1<p≤p1+ p2, r=r2; and if p1+ p2<p≤1, r=r3. In this way, the sender can determine the size of each message group dynamically. It is well known that the PRN sequence depends on the chosen seed for the given generator. Thus, if the receiver exactly knows the adopted PRN generator and the seed, it can also ascertain the size of each message group using the shared “roulette wheel algorithm”. The seed chosen by the sender can be considered as the key for DMES and transmitted together to the receiver beforehand with the parameters in the first part. Accordingly, after receiving all the parameters, the receiver can precisely extract each message group from the cover speech and successfully restitute the whole secret message finally.
[0, 1] using a uniform generator (e.g., Mersenne twister [23]); if p≤p1, set the current size (denoted by r) as r1 in set R1 (or R2), namely, r=r1; if p1<p≤p1+ p2, r=r2; and if p1+ p2<p≤1, r=r3. In this way, the sender can determine the size of each message group dynamically. It is well known that the PRN sequence depends on the chosen seed for the given generator. Thus, if the receiver exactly knows the adopted PRN generator and the seed, it can also ascertain the size of each message group using the shared “roulette wheel algorithm”. The seed chosen by the sender can be considered as the key for DMES and transmitted together to the receiver beforehand with the parameters in the first part. Accordingly, after receiving all the parameters, the receiver can precisely extract each message group from the cover speech and successfully restitute the whole secret message finally.
5 Test and evaluation
The feasibility and effectiveness of DMES were evaluated in StegVoIP that is a prototypical covert communication system based on VoIP [10, 13-14]. StegVoIP supports typical coders, such as ITU-T G.711, G.723.1, G.729a. In this work, G.729a was typically adopted as the codec of the cover speech, while DMES could also effectively work in conjunction with other coders. The selection of LSBs can refer to Refs.[13-14]. In the tests, 8 bits of LSBs were selected in each frame, and the introduction of Huazhong University of Science and Technology [24] was chosen as the secret message. Moreover, 150 audio samples (1 min) were collected, which consisted of three categories: male speeches, female speeches and music. All the samples were recorded with 8 kHz sampling rate, 16 bits quantization and mono, and encoded by G.729a before the embedding process. Each sample provided total 48 000 bits of LSBs, which can be used for the cover bits.
To evaluate the practical performance of DMES, two groups of steganographic experiments on each sample were performed. The experiments in the first group aimed at achieving the desired W(r), while the experiments in the second group focused on achieving the desired D(r). In all the experiments, the search step was set as 0.010 0, and the allowable error was set as 0.001 0. In any case, the secret message (actually only some forward parts) can be successfully embedded and retrieved. For all these experiments, the statistical analysis was made on the average W(r) (denoted by  the average D(r) (denoted by
the average D(r) (denoted by and the average appearance probability of each element in set R (i.e.,
and the average appearance probability of each element in set R (i.e., 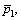
 and
and Furthermore, to measure the dispersions of distributions of α and β from their averages, standard deviation (denoted by σ) was introduced, which was calculated as follows:
Furthermore, to measure the dispersions of distributions of α and β from their averages, standard deviation (denoted by σ) was introduced, which was calculated as follows:
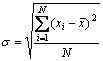
where xi is an element in the given data set; and 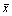 is the average of the given data set.
is the average of the given data set.
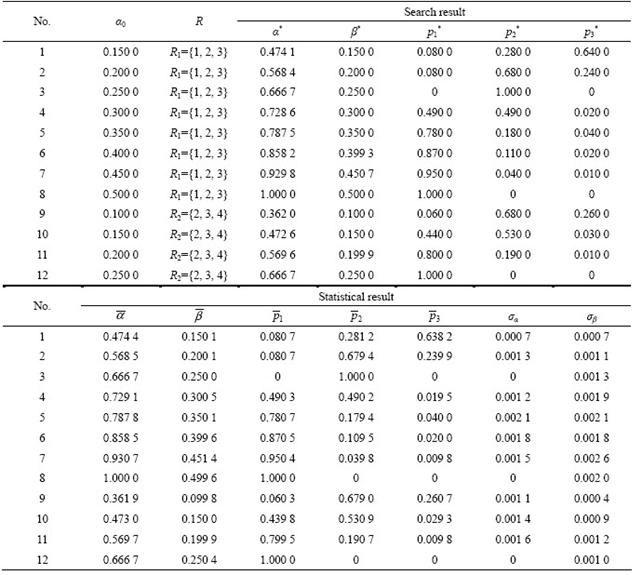
Tables 2 and 3 respectively show the test results of the two groups of experiments. From these data, it can be known that: (1) if one of appearance probabilities is equal to 1.0 and the others are equal to 0 (e.g., when α0=1.000 0 or β0=0.250 0), then DMES is tantamount to the traditional MES. Thus, to a certain degree, the traditional MES can be viewed as a special case of DMES; (2) for the desired W(r) or D(r), the proposed searching algorithm can consistently provide an optimal combination of p1, p2 and p3, which offers dependable guarantee for the practical application of DMES; (3) for α0 [0.428 6, 0.666 7] and β0
[0.428 6, 0.666 7] and β0 [0.125 0, 0.250 0] (e.g., when α0=0.600 0 or β0=0.200 0), two combinations of p1, p2 and p3 can be obtained by employing R1 and R2 respectively. Apparently, both of them can achieve the desired performance, so any one of them can be chosen discretionarily; and (4) in practical applications, the gaps between
[0.125 0, 0.250 0] (e.g., when α0=0.600 0 or β0=0.200 0), two combinations of p1, p2 and p3 can be obtained by employing R1 and R2 respectively. Apparently, both of them can achieve the desired performance, so any one of them can be chosen discretionarily; and (4) in practical applications, the gaps between  and α0 in the first group are not more than 0.000 8, and those between
and α0 in the first group are not more than 0.000 8, and those between  and β0 in the second group are not more than 0.001 4. Moreover, the standard deviations (σα) of the practical W(r) in the first group are not more than 0.002 0, and the standard deviations (σβ) of the practical D(r) in the second group are not more than 0.002 6. These facts indicate that DMES can achieve the desired embedding rate and bit-change rate successfully in any case. Note that DMES is a typical probabilistic method, so the longer the speech sample, the greater the effect. In other words, DMES is especially suitable for steganography on long VoIP conversations.
and β0 in the second group are not more than 0.001 4. Moreover, the standard deviations (σα) of the practical W(r) in the first group are not more than 0.002 0, and the standard deviations (σβ) of the practical D(r) in the second group are not more than 0.002 6. These facts indicate that DMES can achieve the desired embedding rate and bit-change rate successfully in any case. Note that DMES is a typical probabilistic method, so the longer the speech sample, the greater the effect. In other words, DMES is especially suitable for steganography on long VoIP conversations.
Table 2 Test results of the first group that aims at achieving desired W(r)

Table 3 Test results of the second group that aims at achieving desired D(r)
To sum up, DMES can dynamically determine the appearance probabilities of adoptable message sizes, and accordingly regulate embedding rate and bit-change rate effectively and flexibly. That is to say, DMES can consistently achieve the desired embedding capacity and the embedding transparency.
6 Conclusions
(1) Among the proposed methods for enhancing the steganographic transparency, MES can provide the best performance. However, MES cannot totally satisfy the requirements of the steganography based on VoIP since embedding capacity and embedding transparency of MES largely depend on the fixed size of message groups and accordingly cannot be regulated optionally. In order to flexibly adjust embedding capacity and embedding transparency in accordance with requirements of users, a dynamic matrix encoding strategy (DMES) for the VoIP-based steganography is proposed.
(2) DMES significantly extends the traditional MES by dynamically determining the size of each message group according to the desired performance. Overall, DMES consists of two components: searching for an optimal combination of appearance possibilities of all adoptable sizes in accordance with the demand of users, and based on the optimal combination of appearance possibilities, determining the size of each message group by the roulette wheel algorithm.
(3) DMES is evaluated in StegVoIP, a typical covert communication system based on VoIP. The experimental results show that DMES can flexibly adjust the embedding capacity and the embedding transparency, and effectively achieve the desired embedding performance in any case.
(4) In addition, it is worth noting that DMES is codec-independent and cover-independent. Therefore, DMES can be not only applied to the presence of any other coders, but also to the steganography over other carriers, such as image and video.
References
[1] ZHU Cong-xu, CHEN Zhi-gang. A novel spatial domain digital watermarking algorithm based on chaotic map [J]. Journal of Central South University of Technology: Science and Technology, 2005, 36(2): 272-276. (in Chinese)
[2] BADURA S, RYMASZEWSKI S. Transform domain steganography in DVD video and audio content [C]// Proceedings of the 2007 IEEE International Workshop on Imaging Systems and Techniques. Los Alamitos: IEEE, 2007: 1-5.
[3] POOYAN M, DELFOROUZI A. LSB-based audio steganography method based on lifting wavelet transform [C]// Proceedings of the 2007 IEEE International Symposium on Signal Processing and Information Technology. Los Alamitos: IEEE, 2007: 600-603.
[4] LIU Yu-ling, SUN Xing-ming, GAN Can, WANG Hong. An efficient linguistic steganography for Chinese text [C]// Proceedings of the 2007 IEEE International Conference on Multimedia and Expo (ICME’07). Los Alamitos: IEEE, 2007: 2094-2097.
[5] GOODE B. Voice over Internet protocol (VoIP) [J]. Proceedings of the IEEE, 2002, 90(9): 1495-1517.
[6] WANG C, WU Q. Information hiding in real-time VoIP streams [C]// Proceedings of the 9th IEEE International Symposium on Multimedia. Washington: IEEE Computer Society, 2007: 255-262.
[7] DITTMANN J, HESSE D, HILLERT R. Steganography and steganalysis in voice over IP scenarios: Operational aspects and first experiences with a new steganalysis tool set [C]// Proceedings of SPIE, Security, Steganography, and Watermarking of Multimedia Contents VII. Bellingham: SPIE, 2005: 607-618.
[8] KRATZER C, DITTMANN J, VOGEL T, HILLERT R. Design and evaluation of steganography for voice-over-IP [C]// Proceedings of the 2006 IEEE International Symposium on Circuits and Systems (ISACAS’06). Piscataway: IEEE Circuits and Systems Society, 2006: 2397-2340.
[9] HUANG Yong-feng, XIAO Bo, XIAO Hong-hua. Implementation of covert communication based on steganography [C]// Proceedings of the 2008 International Conference on Intelligent Information Hiding and Multimedia Signal Processing (IIHMSP’08). Washington: IEEE Computer Society, 2008: 1512-1515.
[10] TIAN Hui, ZHOU Ke, HUANG Yong-feng, LIU Jin, FENG Dan. A covert communication model based on least significant bits steganography in Voice over IP [C]// Proceedings of the 9th International Conference for Young Computer Scientists (ICYCS’08). Washington: IEEE Computer Society, 2008: 647-652.
[11] AOKI N. A technique of lossless steganography for G.711 telephony speech [C]// Proceedings of the 2008 International Conference on Intelligent Information Hiding and Multimedia Signal Processing (IIHMSP’08). Washington: IEEE Computer Society, 2008: 608-611.
[12] MAZURCZYK W, LUBACZ J. Steganography of VoIP streams [C]// Proceedings of the 3rd International Symposium on Information Security. Berlin: Springer, 2008: 1001-1018.
[13] TIAN Hui, ZHOU Ke, JIANG Hong, HUANG Yong-feng, LIU Jin, FENG Dan. An adaptive steganography scheme for Voice over IP [C]// Proceedings of the 2009 IEEE International Symposium on Circuits and Systems (ISACAS’09). Piscataway: IEEE Circuits and Systems Society, 2009: 2922-2925.
[14] TIAN Hui, ZHOU Ke, JIANG Hong, LIU Jin, HUANG Yong-feng, FENG Dan. An m-sequence based steganography model for Voice over IP [C]// Proceedings of the 2009 IEEE International Conference on Communications (ICC’09). Los Alamitos: IEEE, 2009: 1-5.
[15] XIAO Bo, HUANG Yong-feng, TANG Shan-yu. An approach to information hiding in low bit-rate speech stream [C]// Proceedings of the 2008 Global Telecommunications Conference (GLOBECOM’08). Los Alamitos: IEEE, 2008: 1-5.
[16] M?LLER S, PFITZMANN A, STIRAND I. Computer based steganography: How it works and why therefore any restrictions on cryptography are nonsense, at best [C]// Proceedings of the 1st International Workshop on Information Hiding. Berlin: Springer, 1996: 7-21.
[17] BAI Seng, HU Zhong-yu, WU Le-hua, ZHOU Dao-hua. Steganography of telecommunication information [M]. Beijing: National Defense Industry Press, 2005: 201-202. (in Chinese)
[18] TSENG Y, CHEN Y, PAN H. A secure data hiding scheme for binary images [J]. IEEE Transactions on Communications, 2002, 50(8): 1227-1231.
[19] CRANDALL R. Some notes on steganography [EB/OL]. [2009-12- 01]. http://os.inf.tu-dresden.de/~westfeld/crandall.pdf.
[20] WESTFELD A. F5—A steganographic algorithm [C]// Proceedings of the 4th International Workshop on Information Hiding. Berlin: Springer, 2001: 289-302.
[21] FRIDRICH J, SOUKAL D. Matrix embedding for large payloads [J]. IEEE Transactions on Information Security and Forensics, 2006, 1(3): 390-394.
[22] KHATIRINEJAD M, LISON?K P. Linear codes for high payload steganography [J]. Discrete Applied Mathematics, 2009, 157: 971- 981.
[23] MATSUMOTO M, NISHIMURA T. Mersenne twister: A 623-dimensionally equidistributed uniform pseudorandom number generator [J]. ACM Transactions on Modeling and Computer Simulations: Special Issue on Uniform Random Number Generation, 1998, 8(1): 3-30.
[24] An introduction of Huazhong university of science and technology [EB/OL]. [2009-12-08]. http://english.hust.edu.cn/about_overview. html.
(Edited by CHEN Wei-ping)
Foundation item: Project(2009AA01A402) supported by the National High-Tech Research and Development Program of China; Project(NCET-06-0650) supported by Program for New Century Excellent Talents in University; Project(IRT-0725) supported by Program for Changjiang Scholars and Innovative Research Team in Chinese University
Received date: 2010-01-23; Accepted date: 2010-04-16
Corresponding author: ZHOU Ke, PhD, Professor; Tel: +86-13971075916; E-mail: raidkick@263.net