文章编号:1004-0609(2010)12-2406-06
相场法模拟多个空间取向的棒状第二相粒子对
晶粒长大的影响
罗志荣1,高英俊1, 2,邱鸿广1,张海林1
(1. 广西大学 物理科学与工程技术学院,南宁 530004;
2. 中国科学院 国际材料物理中心,沈阳 150016)
摘 要:采用相场法研究多个空间取向的棒状第二相粒子以及圆形第二相粒子对基体晶粒长大的影响。结果表明:在晶粒长大过程中,绝大部分棒状第二相粒子位于晶界处并与晶界方向一致,圆形第二相粒子大多位于三晶交点处;第二相粒子表现出强烈的钉扎晶界的作用,极限晶粒半径可以用Zener关系表示;在第二相粒子面积分数和粒子尺寸相同的情况下,当第二相粒子面积分数较小(<5%)时,棒状与圆形第二相粒子对晶粒长大的钉扎作用没有明显差别;当粒子面积分数较大(>5%)时,棒状第二相的钉扎效果好于圆形第二相的钉扎效果。
关键词:相场法;晶粒长大;第二相粒子;Zener钉扎
中图分类号:TG111.5 文献标志码:A
Effect of stick second-phase particles with different geometric
orientations on grain growth simulated by phase field method
LUO Zhi-rong1, GAO Ying-jun1, 2, QIU Hong-guang1, ZHANG Hai-lin1
(1. School of Physics Science and Engineering, Guangxi University, Nanning 530004, China;
2. International Center for Materials Physics, Chinese Academy of Sciences, Shenyang 150016, China)
Abstract: The phase-field method was applied to simulating the effect of the second-phase particle with different geometric orientations and spherical second-phase particles (SPP) on the matrix grain growth. The results show that, in the grain growth process, most of the spherical SPP locate in the intersection of crystal boundary, while stick SPP locate in the grain boundary with the same direction as the grain boundaries. The SPP show a strong pinning effect on grain boundary and the limiting grain radius can be expressed by Zener relations. Under the condition that the SPP area fraction and size are constants, there is no difference between stick SPP and spherical SPP in the pinning effect on grain growth when the area fraction of the SPP is small(<5%), however, compared to spherical SPP, the stick SPP show more effective pinning effect when the area fraction of the SPP is large(>5%).
Key words: phase field method; grain growth; second-phase particles; Zener pinning
同时提高金属材料的强度和韧性的最有效方法是细化晶粒,而利用弥散分布的第二相粒子细化基体组织已成为工业上常用的强化方法。第二相粒子具有钉扎晶界的能力,对单相多晶材料的晶粒长大具有很大的影响,其通过限制晶界的移动性,最终使晶粒停止长生,晶粒达到极限尺寸[1]。
现已有很多关于第二相粒子钉扎对晶粒长大作用的理论模型[2-7]和方法[8-13]。MOELANS等[14-15]在CHEN和YANG[16]提出的相场模型的基础上首次构建了包含第二相粒子的相场模型,研究第二相粒子对晶粒长大的钉扎作用规律。SUWA和SAITO[17]模拟三维情况下第二相粒子对晶粒长大的作用。高英俊等[18]将MOELANS等[15]提出的模型推广到硬质颗粒对两相晶粒长大钉扎的作用体系。龙永强等[19]研究球形和盘形第二相粒子对晶粒长大的影响。但目前通过相场法系统研究具有多个空间几何取向和形状的第二相粒子对基体晶粒长大过程影响的工作鲜见报道。本文作者应用扩散界面相场动力学模型,系统研究具有多个空间几何取向的棒状第二相粒子对正常晶粒长大的钉扎作用规律。
1 模型的建立
在单相多晶材料晶粒演化的相场模型[16]中,用一组非保守的取向场变量η1(r,t),η2(r,t),…,ηP(r,t)来描述不同的晶粒取向,其中ηi(i=1,2,…,P)代表取向场变量,P为总取向数。根据MOELANS等[14-15]提出的包含第二相粒子的体系自由能模型来描述某一特定形状和尺寸的粒子对晶粒长大的影响,系统的自由能为
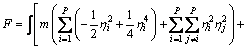
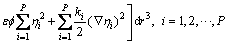 (1)
(1)
式中: 仅是一个与位置相关的函数,并且要求在基体中
仅是一个与位置相关的函数,并且要求在基体中 =0,在第二相粒子内部
=0,在第二相粒子内部 =1。
=1。
取向场变量ηi为非保守变量,它们的演化规律可以利用Ginzburg-Landau方程组描述:

 (2)
(2)
式中:Li为与晶界迁移率有关的动力学系数。
本文作者研究在二维情况下的晶粒演化,将计算区域离散为正方形网格,采用周期性边界条件。初始取向场变量ηi值取在[-0.001,0.001]之间的随机数,代表初始形貌。在晶粒形核前,第二相粒子已预先弥散分布于系统中,粒子大小保持不变。为了能更加真实反映第二相粒子的实际形状,采用圆形和棒状两种常见的第二相粒子;棒状第二相粒子取4个空间取向角度,与横轴夹角分别为0°、45°、90°、135°,4种角度的棒状第二相粒子所占比例相等。为了保证对不同形状第二相粒子钉扎作用的模拟结果具有可比性,在初始化过程中,设置第二相形态时,含有棒状和圆形粒子的粒子尺寸、面积分数以及分布相同。模拟参数如下:网格节点数为300×300 g.p.(g.p.表示格子点数),P=36,m=ε=1.0,ki=2.0,Li=1.0,时间步长Δt=0.25,空间步长Δx=2.0 g.p.。另外,为了直观地显示晶粒形貌,引入可视变量ψ(r,t)[16]
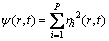 (3)
(3)
来描述整个系统的演化。当ψ=0时,微观结构为黑色;ψ=1时,微观结构为白色。
2 模拟结果
图1所示为棒状和圆形第二相粒子在面积分数fa都为2%时晶粒组织的演化过程。从图1(a)~(f)的形貌可以看出,随着模拟时间的增加,出现大晶粒吞并小晶粒的现象,但由于第二相粒子的存在,晶粒的晶界被第二相粒子钉扎。在初始阶段,当晶粒在长大过程中遇到第二相粒子时,晶粒边界被第二相粒子钉扎,所有粒子位于晶界处(见图1(a)和(d));随着晶粒的不断长大,少数晶粒的晶界能够摆脱第二相粒子的钉扎(见图1(c)中的点A和B处与图1(f)中的点C和D处)。随着晶粒的演化,晶界逐渐平直,其摆脱第二相粒子钉扎的驱动力也变得越来越弱。所以,在最终得到的微观组织中,大多数第二相粒子仍位于晶界处,晶界均呈平直形。由于晶粒间的晶界有伸直的趋势,使晶粒的长大速度变慢,最终使晶粒停止长大。
图2所示为含圆形和棒状第二相粒子不同面积分数的晶粒系统的微观结构(其中第二相粒子面积分数fa=5%,模拟时间t=2.3×104)。由图2(a)~(c)可见,大部分圆形第二相粒子位于三晶交叉处,而棒状第二相粒子大多位于晶界处,其方向与晶界线方向一致。这是因为单相多晶系统晶粒演化的驱动力来源于系统界面能的减少,而第二相粒子位于晶界使得界面能降低,所以,当圆形第二相粒子占据三晶交叉处,棒状第二相粒子位于晶界且方向与晶界方向一致时,系统的晶界面积减少最多,系统界面能最小,这符合系统的演化趋势。
3 分析与讨论
3.1 第二相粒子形状对晶粒长大的影响
为研究圆形和多个空间取向的棒状第二相粒子对晶粒长大的影响,对模拟的微观结构演化图中平均晶

图1 棒状和圆形第二相粒子在面积分数fa为2%时的晶粒组织演化过程
Fig.1 Microstructures evolution of system containing stick SPP and spherical SPP at area fraction (fa) of 2%: (a) Stick SPP, t=300; (b) Stick SPP, t=3×103; (c) Stick SPP, t=1.5×104; (d) Spherical SPP, t=300; (e) Spherical SPP, t=3×103; (f) Spherical SPP, t=1.5×104
粒尺寸随时间的变化进行统计分析,其结果如图3所示,其圆形和棒状第二相粒子的粒子等效半径r均为3.3 g.p.。图3(a)、(b)、(c)中第二相粒子的面积分数分别为5%、8%和10%。
从图3(a)可以看出,在第二相粒子含量较小(fa=5%)时,含不同形状第二相粒子的晶粒长大曲线几乎重合,表明第二相粒子的形状对系统平均晶粒尺寸的影响很小。这是因为第二相粒子含量较少时,没有被钉扎的晶界多,大多数晶粒可以自由长大,所以第二相粒子的形状对晶粒的长大以及对晶界的钉扎效果没有明显的影响,与文献[19]的结果相一致。
由图3(b)~(c)可见,在第二相粒子含量较多(fa>5%)时,第二相粒子含量越多,两类曲线分离越明显。在相同模拟时间下,棒状比圆形第二相粒子的晶粒平

图2 第二相粒子面积分数fa为5%和模拟时间t为2.3×104时含圆形和棒状第二相粒子不同比例系统的显微组织模拟
Fig.2 Microstructures simulation of system containing stick SPP and spherical SPP at area fraction (fa) of 5% and time steps t =2.3×104: (a) Spherical SPP, 5%; (b) Spherical SPP, 3%+stick SPP, 2%; (c) Stick SPP, 5%
均尺寸小,说明棒状第二相粒子钉扎效果比圆形第二相粒子更好。因为圆形第二相粒子是等轴粒子,其空间对称性好而没有取向差异,对晶粒演化的限制较小;棒状第二相粒子是非等轴粒子,在基体中就会有一定的空间几何取向。由图1(c)和2(c)可以发现,晶界与棒状第二相粒子之间的接触几乎都是线接触,晶粒沿垂直于棒状第二相粒子长度方向的长大过程受到抑制,使晶界呈现方向性,所以棒状第二相粒子对于晶粒组织长大的钉扎作用必然大于圆形第二相粒子的,其细化晶粒的效果好于圆形第二相粒子。该结论与文献[6]的实验和理论结果相一致。
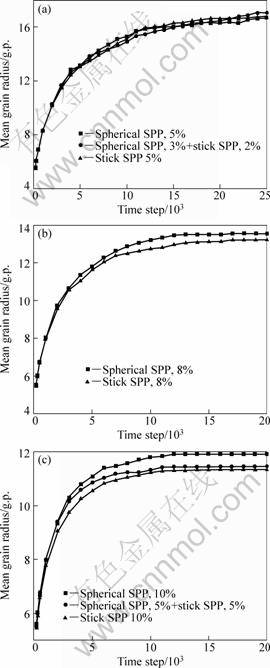
图3 含不同形状第二相粒子系统中平均晶粒半径随时间的变化
Fig.3 Changes of mean grain radius with time for system containing SPP: (a) fa=5%; (b) fa=8%; (c) fa=10%
3.2 晶粒生长指数
图4所示为含不同面积分数的第二相粒子系统中在t<6×103时晶粒平均半径随时间的变化曲线。由图4可见,在6种不同第二相粒子面积分数下,系统中晶粒平均半径随演化时间的增加而逐渐增大,即晶粒个数逐渐减少。但第二相粒子面积分数越小,相同时刻晶粒平均半径越大,晶粒个数越少。这说明第二相粒子面积分数越小,其对晶界钉扎效果越不明显,晶粒长大速度就越快。当第二相粒子面积分数较大(fa>8%)时,晶粒半径很快趋于极限半径。利用晶粒生长规律公式进行拟合,得到第二相粒子占不同面积分数的晶粒生长指数规律,其结果见表1。由表1可见,面积分数从0增加到10%,圆形第二相粒子的生长指数m则从1.99单调增加到3.33,棒状第二相粒子的生长指数m则从1.99单调增加到3.53。晶粒生长指数越大,表示晶粒生长速度越慢。在晶粒长大初期,当第

图4 含不同面积分数第二相粒子系统中晶粒平均半径随时间变化的拟合曲线
Fig.4 Fitting curves of average grain size of stick (a) and spherical (b) SPP vs time
表1 晶粒生长指数公式中参数随第二相粒子面积分数的 变化
Table 1 Variation of parameters in grain growth exponent formulate for stick and spherical SPP

二相面积分数较小时,圆形第二相粒子的生长指数与棒状第二相粒子生长指数几乎相同;当fa=10%,两者才有明显不同。与文献[18]的结果比较可知,第二相粒子钉扎的晶粒生长指数要比第三相粒子钉扎的两相晶粒生长指数要小。
3.3 第二相粒子对极限晶粒尺寸的影响
按照Zener关系用最小二乘法拟合曲线,得到在不同面积分数(1%≤fa≤15%)第二相粒子作用下,晶粒极限半径和第二相粒子半径的比值Rlim/r(φ)与第二相粒子面积分数fa的关系曲线(见图5),对应的关系式为
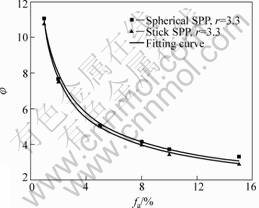
图5 极限晶粒半径与第二相粒子等效半径的比率φ与第二相粒子面积分数fa的关系
Fig.5 Relationship between φ and area fraction (fa) of SPP
 (4)
(4)
模拟所得结果与MOELANS等[15]的模拟结果β=1.31(±0.12),b=0.49(±0.02)一致。从图5可见,在相同条件下,棒状第二相粒子的极限半径小于圆形第二相粒子的极限半径,说明棒状第二相粒子比圆形第二相粒子的钉扎效果更好。
4 结论
1) 晶粒长大过程中,绝大部分圆形第二相粒子位于三晶交点处,棒状第二相粒子位于晶界处并与晶界方向较好地保持一致,第二相粒子表现出强烈钉扎晶界的作用。基体晶粒的极限尺寸与第二相粒子面积分数有如下关系:对于棒状第二相粒子有φ= 1.18fa-0.48;对于圆形第二相粒子有φ=1.27fa-0.47。
2) 在含第二相粒子的系统中,晶粒生长符合指数生长规律,其生长指数要比第三相粒子钉扎的两相晶粒生长指数小。
3) 当体系中第二相粒子面积分数较小时,棒状与圆形第二相粒子对晶粒长大的钉扎作用没有明显差别;当体系中第二相粒子面积分数较大时,棒状第二相粒子钉扎效果好于圆形第二相粒子。
REFERENCES
[1] RYUM N, HUNDERI O, NES E. On grain boundary drag from second phase particles[J]. Scripta Metallurgica, 1983, 17(11): 1281-1283.
[2] MANOHAR P A, FERRY M, CHANDRA T. Five decades of the zener equation[J]. ISIJ International, 1998, 38(9): 913-924.
[3] HILLERT M. Inhibition of grain growth by second-phase particles[J]. Acta Metallurgica, 1988, 36(12): 3177-3181.
[4] BRECHET Y, MILITZER M. A note on grain size dependent pinning[J]. Scripta Materialia, 2005, 52(12): 1299-1303.
[5] WANG X L, WEI Y H, WANG W, HOU L F. Calculation of second phase particle-grain boundary interaction range[J]. Acta Metallurgica Sinica (English Letters), 2008, 21(1): 8-14.
[6] RINGER S P, LI W B, EASTERLING K E. On the interaction and pinning of grain boundaries by cubic shaped precipitate particles[J]. Acta Metallurgica, 1989, 37(3): 831-841.
[7] LI W B, EASTERLING K E. The influence of particle shape on zener drag[J]. Acta Metallurgica et Materialia, 1990, 38(6): 1045-1052.
[8] HARUN A, HOLM E A, CLODE M P, MIODOWNIK M A. On computer simulation methods to model Zener pinning[J]. Acta Materialia, 2006, 54(12): 3261-3273.
[9] APEL M, BOTTGER B, RUDNIZKI J, SCHAFFNIT P, STEINBACH I. Grain growth simulations including particle pinning using the multiphase-field concept[J]. ISIJ international, 2009, 49(7): 1024-1029.
[10] 柯常波, 张新平. 第二相颗粒对多晶材料晶粒生长影响的元胞自动机(CA)模拟[J]. 中国有色金属学报, 2009, 19(12): 2173-2178.
[11] KE Chang-bo, ZHANG Xin-ping. Cellular automata modeling of influence of second-phase particles on two-dimension grain growth in polycrystalline materials[J]. The Chinese Journal of Nonferrous Metals, 2009, 19(12): 2173-2178.
[12] COUTURIER G, MAURICE C, FORTUNIER R. Three- dimensional finite-element simulation of Zener pinning dynamics[J]. Philosophical Magazine, 2003, 83(30): 3387-3405.
[13] 刘祖耀, 郑子樵, 陈大钦, 李世晨. 正常晶粒长大的计算机模拟(Ⅱ)——第二相粒子形.状及取向的影响[J]. 中国有色金属学报, 2004, 14(1): 122-126.
[14] LIU Zu-yao, ZHENG Zi-qiao, CHEN Da-qin, LI Shi-chen. Computer simulation of grain growth(Ⅱ)—Influence of shape and orientation of second-phase particles on grain growth[J]. The Chinese Journal of Nonferrous Metals, 2004, 14(1): 122-126.
[15] WEYGAND D, BRECHET Y, LEPINOUX J. Zener pinning and grain growth: A two-dimensional vertex computer simulation[J]. Acta Materialia, 1999, 47(3): 961-970.
[16] MOELANS N, BLANPAIN B, WOLLANTS P. A phase field model for the simulation of grain growth in materials containing finely dispersed incoherent second-phase particles[J]. Acta Materialia, 2005, 53(6): 1771-1781.
[17] MOELANS N, BLANPAIN B, WOLLANTS P. Phase field simulations of grain growth in two-dimensional systems containing finely dispersed second-phase particles[J]. Acta Materialia, 2006, 54(4): 1175-1184.
[18] CHEN L Q, YANG W. Computer simulation of the domain dynamics of a quenched system with a large number of nonconserved order parameters: The grain-growth kinetics[J]. Phys Rev B, 1994, 50(21): 15752-15756.
[19] SUWA Y, SAITO Y. Phase field simulation of grain growth in three dimensional system containing finely dispersed second-phase particles[J]. Scripta Materialia, 2006, 55(4): 407-410.
[20] 高英俊, 张海林, 金 星, 黄创高, 罗志荣. 相场方法研究硬质粒子钉扎的两相晶粒长大过程[J]. 金属学报, 2009, 45(10): 1190-1198.
[21] GAO Ying-jun, ZHANG Hai-lin, JIN Xing, HUANG Chuang-gao, LUO Zhi-rong. Phase-field simulation of two-phase grain growth with hard particles[J]. Acta Metallrugica Sinica, 2009, 45(10): 1190-1198.
[22] 龙永强, 刘 平, 刘 勇, 潘建生. 相场法模拟球形和盘形第二相粒子对晶粒长大的影响[J]. 中国有色金属学报, 2009, 19(1): 84-89.
[23] LONG Yong-qiang, LIU Ping, LIU Yong, PAN Jian-sheng. Phase field modeling for effects of spherical and discal second-phase particles on grain growth[J]. The Chinese Journal of Nonferrous Metals, 2009, 19(1): 84-89.
(编辑 李艳红)
基金项目:国家自然科学基金资助项目(50661001,50061001);广西省自然科学基金资助项目(0991026, 0832029,0639004)
收稿日期:2009-11-11;修订日期:2010-07-10
通信作者:高英俊,教授,博士;电话:0771-3239478;E-mail:gaoyj@gxu.edu.cn