DOI：10.19476/j.ysxb.1004.0609.2017.10.18

基于反向步长递减算法铝厚板预拉伸夹持区的预测方法

秦国华，王志刚，林  锋，叶海潮

(南昌航空大学 航空制造工程学院，南昌 330063)

摘  要：预拉伸是消除铝合金板材内淬火残余应力的主要方法，但拉伸机夹钳对板材两端的夹持不仅影响着板材端部残余应力的消除效果，而且还涉及到拉伸后板材的锯切量、成材率等问题。因此，通过研究铝合金板材预拉伸本构模型、边界条件、失效准则等关键技术，建立了极限下压量和滑移因子的有限元分析方法。其次，通过构造初始夹持长度的计算函数，以一定步长正向从初始夹持长度继续取值，根据当前值与上一次取值之间滑移因子的差异，确定下一次取值的步长及其方向；若滑移因子相同则以相同步长继续正向取值，否则以递减的步长反向取值，直至步长的绝对值在阈值范围之内，构建最小夹持长度反向步长递减的确定算法，以此获得板材厚度、伸长率为输入的神经网络训练样本。借助神经网络的非线性映射能力，通过有限组的训练样本，构建了最小夹持长度的神经网络预测模型。将预测值与相应的有限元仿真值进行比较，结果表明预测误差在5%以内，进一步验证建立的工件变形预测模型具有合理性。

关键词：铝合金厚板预拉伸；极限下压量；滑移因子；最小夹持长度；反向步长递减

文章编号：1004-0609(2017)-10-2105-09　　     中图分类号：TG156；TP391.9　　     文献标志码：A

整体结构件旨在实现减轻质量、增加效率、降低成本、提高可靠性等目的，在飞机大型化发展的趋势下得到了越来越广泛的应用^[1-2]。另一方面，铝合金厚板作为大型铝合金型材的一种，目前在机翼壁板、隔框、翼梁、翼肋等飞机结构件上进行了广泛使用^[3-4]。预拉伸是铝合金板材成形制造的重要工艺，通过在轧制方向对淬火铝合金厚板进行一定的预拉伸实现淬火残余应力的消除，业已成为消除残余应力的重要手段^[5]。

铝合金板材预拉伸工艺研究主要集中在两个方面。一是拉伸工艺对残余应力的消除。铝合金厚板内存在的残余应力导致整体结构件切削成形过程中出现弯曲、扭曲等变形，当变形过大以致无法将飞机结构件校正到精度要求范围而报废^[6]。宋寒等^[7]利用裂纹柔度法测量25 mm厚的7055-T7751铝合金预拉伸板内残余应力，获得了外压内拉的“W”应力分布形式，通过与其它两种7xxx系列板材残余应力进行对比后，认为7055铝合金材料在提高性能的同时，残余应力也相应提高，最终导致7055铝合金航空结构件加工变形较大。郑林等^[8]通过无损测定25 mm厚的国产2024-T351预拉伸板和20 mm厚的美国7075-T651预拉伸板内厚向残余应力和织构分布，比较分析后认为内部织构的不均匀性，使得铝厚板在预拉伸过程中产生不均匀的塑性变形，是导致国产铝厚板残余应力消除效果差的关键因素。龚海等^[9]分析了不同伸长量对淬火铝厚板内残余应力的消除效果，认为2.2%左右的伸长量能够达到应力消减的最佳效果。袁望姣等^[10]研究了伸长量对不同厚度铝合金板材的残余应力消除效果，认为伸长量越大，残余应力越小，而铝板越厚，残余应力越大。朱才朝等^[11]分析了板材厚度、伸长量对残余应力的影响规律，认为随着铝合金板材厚度的增加，达到更好消除效果的伸长量也应增大。TANNER等^[12]对7075铝合金进行了伸长量为2%的预拉伸模拟，与压缩消除残余应力结果进行对比后认为拉伸比压缩具有更好的残余应力消除效果。另一则是研究预拉伸夹持对板材塑性变形的影响。拉伸后的铝合金板材依据塑性变形特点可分为夹持区、过渡变形区和均匀变形区，拉伸机夹钳对板材两端的夹持涉及到拉伸后板材的残余应力消除效果、锯切量、成材率等问题。朱才朝等^[13]分析了伸长率消除厚度为12 mm铝合金板材内残余应力的规律，认为最适宜的伸长率为1.0%，而且得出过渡变形区长度约为板材厚度的67%。李淑明等^[14]对淬火铝厚板仿真了伸长量为1.8%、2.0%、2.5%的预拉伸过程，比较后得出伸长量2.0%~2.5%为理想拉伸区间，并依据等效应力分布实现锯切区的确定。辜蕾钢等^[15]研究了伸长率为2.3%的铝合金板材塑性变形规律，结果表明不是板材所有的区域都达到了美国铝业协会规定的消除淬火残余应力要求的1%~3%变形量：塑性变形为0的区域显然属于夹持区，在据板材左端430 mm处，由于塑性变形均超出1%，是为均匀变形区，两者之间则为过渡区(如据板材左端425 mm处塑性变形不完全超出1%)。

在进行预拉伸消除残余应力时，无论是铝合金板材生产企业还是理论研究，工艺参数照搬国外数据，既没有深入了解拉伸后板材内部应力的分布状态，也没有给出锯切量和成材率的清晰判定，造成大量的浪费。因此，本文作者在铝厚板预拉伸前期研究工作^[2]的基础上，依据预拉伸过程中夹钳下压时的材料失效，通过获得夹钳的极限下压量后，研究夹钳拉伸时的最小夹持面积，提出极限下压量下最小夹持长度的反向步长递减算法。然后，通过有限组的训练样本，构建以伸长率和板材厚度为输入变量的最小夹持长度神经网络预测方法，避免锯切量的浪费。

1  预拉伸分析机理

对于淬火后7075铝合金板材，在夹持力不破坏板材的前提条件下，通过拉伸机给予1%~3%左右的塑性变形，使板材内部沿厚度在轧制方向上的残余应力进行重新分布。无论是受压应力的表层金属，还是受拉应力的内层金属，在受到外力的作用后都将发生变形，当给予的拉伸力超过该金属的弹性极限后，就发生塑性变形。由于板材的内层金属原来就具有残余拉应力，所以它首先超过弹性极限进入塑性变形，这就造成了内层金属的变形速度比外层(表层)快，又由于板材仍是一个整体，表层金属会牵制内层金属的变形，所以在塑性变形发生后，表层金属将产生拉应力，内层金属将产生压应力，这正好和淬火后的板材的残余应力方向相反。当外力去除后，板材弹性应变松弛，此时板材中残余应力就将是淬火后板材中的残余应力与拉伸变形时所产生的内应力之差，如果伸长量选择合适，其差可以接近于零，即可以消除残余应力。

1.1  预拉伸本构模型

铝合金板材的预拉伸包括夹钳的下压以及夹钳的拉伸两个过程，如图1所示。无论是压，还是拉，铝合金板材在弹性范围的应力应变关系均符合广义胡克定律，即

                                    (1)

式中：为等效应力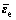；为等效弹性应变；D为由弹性模量E和泊松比υ确定的弹性矩阵。

根据Mises屈服准则可知，当应力满足条件

                                     (2)

则板材发生塑性变形。其中：σ_b为屈服极限。

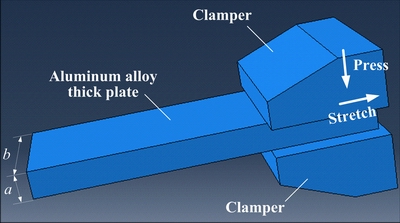
图1  铝合金板材预拉伸的示意图

Fig. 1  Schematic diagram of pre-stretching of Al alloy sheet

当应力σ超过屈服极限后，塑性区域应按增量理论计算，此时应变量由弹性应变增量和塑性应变增量组成

                               (3)

式中：dε为应变增量；dε_e为弹性应变增量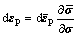；为塑性应变增量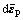；为等效塑性应变增量。

1.2  边界条件

在夹持力不破坏材料的前提下，铝合金板材的预拉伸过程，主要是通过夹钳与板材之间的摩擦力使得板材得到拉伸。板材在拉伸过程中的受力状态如图2所示，当且仅当板材在夹钳夹持下拉伸不打滑的条件为

F≤                                       (4)

式中：N为夹持力；F为摩擦力；μ为板材与夹钳之间的摩擦因数。

事实上，在满足式(4)的拉伸不打滑时，板材和夹钳上的任意一个接触点A，其相对位移应为0。因此，定义一个滑移因子Ψ来衡量拉伸的滑移性，即

                                (5)

式中：判定因子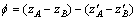；z_A、为板材上任意点A在拉伸前、拉伸后的坐标；z_B、为夹钳上任意点B的位移。

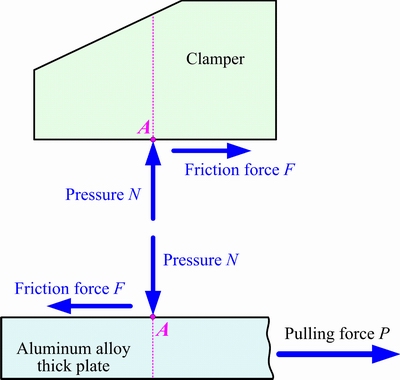
图2  板材拉伸时的受力状态

Fig. 2  Force state of sheet pre-stretching

显然，当且仅当滑移因子Ψ=0时，拉伸不具有滑移性，也就是说，拉伸时不打滑。

1.3  失效准则

根据等效塑性应变准则可知，工件材料的状态变量表明材料失效，此时是板材在拉伸或下压作用下出现断裂现象的分水岭。工件材料的状态变量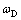可描述为

                                          (6)

式中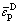：为失效应变(即临界值)，是应力三维度和等效塑性应变率的函数，由单向拉伸或压缩实验确定；η为应力三维度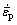；为等效塑性应变率。

1.4  有限元仿真方法

待预拉伸的板材尺寸为1200 mm×220 mm×50 mm，材料为7075铝合金，其材料参数^[10]见表1所列。夹钳和板材之间的摩擦因数为μ=0.4^[11]。

首先确定出不破坏板材的极限下压量。当夹钳向板材下压时，夹持力引起的下压量超过极限下压量，则板材出现裂缝而失效。

表1  7075铝合金材料参数

Table 1  Material parameters of 7075 aluminum alloy

根据式(1)~(3)和式(6)，结合表1数据，建立夹钳的下压有限元分析模型。模型中定义夹钳为刚体，采用C3D4单元划分网格，而板材采用局部网格加密技术进行网格划分，在板材与夹钳交界部位采用C3D8R单元细分网格，其他部位则采用C3D4单元，网格向两者交接部位由大到小逐渐密集，如图3(a)所示。由式(6)可知，失效准则的依据是制定的某个或某些物理量(如等效塑性应变)达到临界值，一般在0.4~0.6取值作为临界值^[16]，这里选择临界值为0.5。经有限元方法计算后可得极限下压量为Δ_max=2.4 mm，如图3(b)所示。

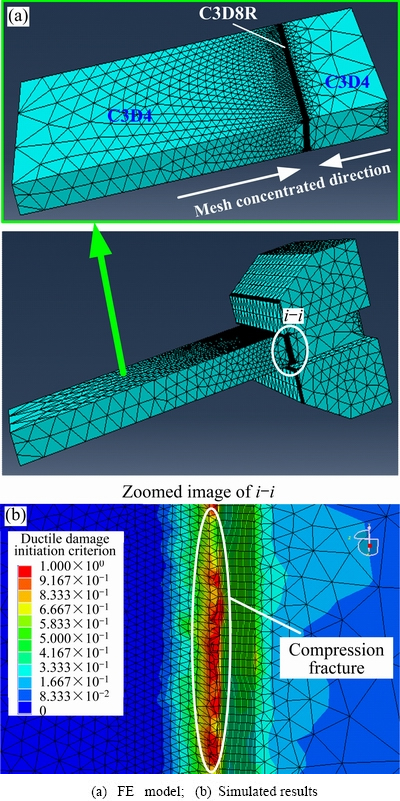
图3  下压有限元分析

Fig. 3  FEA of compressing stage

其次，分析出极限下压量的夹持合理性。夹持合理性指的是在不破坏板材材料的情况下，预拉伸板材到一定伸长量时夹钳对板材夹持的滑移性。铝合金板材无论是几何结构还是拉伸受力状态均关于轧制方向和纵向方向对称，因此只需确定相应的边界条件就可将模型简化为原来的1/2进行分析。这里，认为拉伸过程非常缓慢，不考虑拉伸速度的影响。铝合金板材与夹钳分别采用C3D8R单元和C3D4单元进行网格划分，图4为伸长率为1.8%的有限元分析模型及其结果，其中点A、B为板材和夹钳上的观测点，坐标分别为r_A=[181.25 mm, 20 mm, 100 mm]^T和r_B=[221.25 mm, 20 mm, 200 mm]^T。

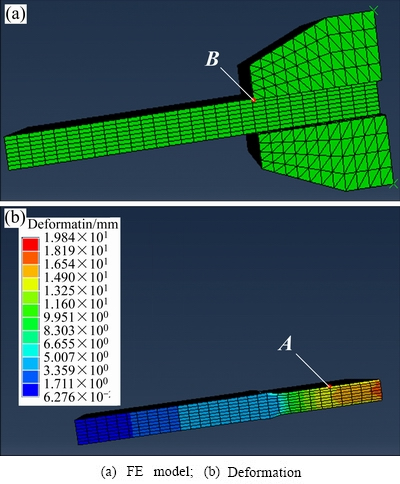
图4  预拉伸有限元分析

Fig. 4  FEA of pre-streching stage

根据有限元仿真结果，可知拉伸后A、B两点的坐标为r_A=[188.9 mm, 16.6 mm, 189.2 mm]^T和r_B=[221.25 mm, 16.6 mm, 189.2 mm]^T。

2  反向步长递减算法

夹头下压时，在夹持力不破坏板材的条件下，应尽可能少地夹持板材进行拉伸，以使夹持区面积小，过渡区面积也将随之变小，从而节约材料。由于夹持宽度b一定，因此使得夹持面积越小，则应使得夹持长度越小。

2.1  算法的构造

对于根据式(1)~(3)，式(6)确定的临界下压量Δ_max，求解一定伸长量δ的最小夹持长度L_min的本质，就是搜索出满足式(1)~(5)的临界值^[17-18]。

在确定夹持长度L₀的初始近似值时，可根据式(5)判断L₀的滑移性，不滑移则令方向标识为λ₀=0，滑移则λ₀=1。

选取步长s₁=s(s为任意给定的初始步长)，求出L₁=L₀+s，称L₁为L_min的一次近似值。判断L₁的滑移性，不滑移则令λ₁=1，若滑移，令λ₁=0。定义δ₁=λ₁-λ₀为滑移性的方向变化，若δ₁=0方向无变化。

如果滑移性没有发生方向变化，则按照大小、方向均不变的原则确定下一个夹持长度近似值，此时L₂=L₁+s，称L₂为L_min的二次近似值；如果可行性发生了方向变化，则按照大小递减(递减系数为ζ＜1。这里取ζ=0.5)、方向相反的原则确定下一个夹持长度近似值，即夹持长度的二次近似值为L₂=L₁-s/2，当前步长s=-s/2。

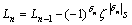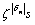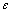重复以上过程，得L_min的近似值序列，其中，称为L_min的n次近似值，该式称为变向迭代公式，而当前步长。当且仅当≤(阈值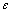为任意给定的正数，一般取较小值)，迭代过程结束，L_n即为L_min的最终近似值。

综上所述，夹持长度初始近似值L₀的确定关系着整个算法的收敛速度。由于板材在预拉伸过程中发生弹塑性变形，为此拟采用材料的屈服极限来估算夹持长度的初始近似值L₀。由图2可知，拉伸应力超过屈服极限时，板材发生塑性变形，此时存在下列关系

                                 (7)

式中：a、b为板材的厚度和宽度；L为夹持长度。

整理式(7)可知，夹持长度L的初始值L₀可按下式选取

                            (8)

式中：ceil(*)为向上取*整数的圆整函数。

2.2  应用与分析

由于夹钳在极限下压量时等效应力=140，故依据式(8)取初始夹持长度L₀=200 mm。在给定步长s=30和阈值=0.15时，最佳夹持长度的计算过程如表2所列，直至算到第11步，此时当前步长小于给定阈值(即0.1171875＜0.15)，计算结束，最佳夹持长度应为L_min=193.2 mm。

表2  7075铝合金材料参数

Table 2  Material parameters of 7075 aluminum alloy

3  神经网络预测方法

在板材厚度、伸长量等参数均给定的条件下，有限元方法可以用来分析预拉伸过程，获得板材的残余应力、塑性变形、拉伸滑移等信息。然而，板材厚度、伸长量的组合工艺多种多样，不可能利用有限元方法一一进行计算，但神经网络可以找出预拉伸工艺参数与夹持长度之间的复杂关系。

3.1  神经网络结构

BP神经网络是一种具有三层及以上的前馈神经网络，包括输入层、隐藏层和输出层，可任意的精度逼近任意的连续函数。

由此，可以采用1个三层BP神经网络进行夹持长度的预测，其结构如图5所示。在板材预拉伸过程中，影响夹持长度的印度很多，这里主要考虑板材厚度、伸长率等两个主要工艺参数作为输入层的神经元，故u=2，而需预测的夹钳夹持板材不滑脱的最小夹持长度则为输出层的神经元，此时w=1。再根据Kolmogorov定理，隐藏层的神经元数目v可按照下列经验公式^[19]确定，即

                                   (9)

由此可见，隐藏层应有5个神经元。

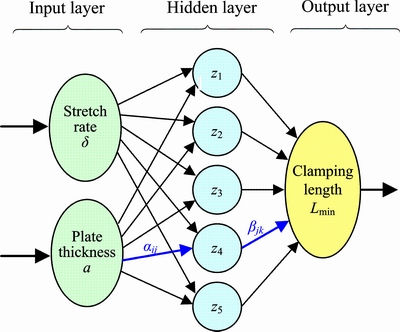
图5  神经网络结构

Fig. 5  Configuration of neural network

3.2  训练样本

板材在拉伸过程中，塑性变形是由局部开始逐渐向整体扩展的，其均匀变形的程度直接受钳口状态和变形速度的影响与制约。每张板材内部都存在着微观不均匀性，而且对拉伸后应力场的分布具有很大影响。因此，宏观变形量既要保证消除板材内的淬火残余应力，又要避免过大的伸长量引起的附加应力。航空工业所用的铝合金厚板生产工艺规定^[20]：拉伸产生2%的永久变形，但不能小于1.4%，也不能大于3%。这样，针对厚度为20~50 mm的板材，确立了16组神经网络的输入样本，方案和板材夹持长度如表3所列。

由表3数据可以看出，最小夹持长度与铝板厚度、

表3  板材拉伸方案与实验数据

Table 3  Pre-stretching schemes and experimental data

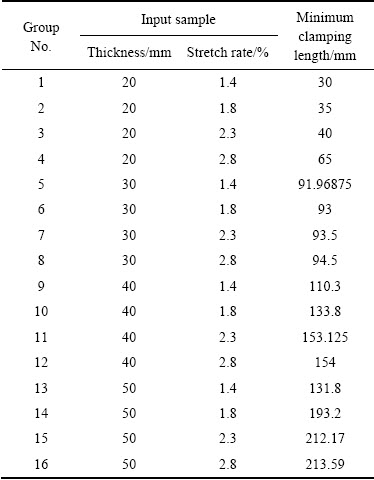
伸长率有着明确关系。伸长率一定的条件下，铝板厚度越大，夹持长度也越大；同样，板材厚度一定，随着伸长率的增大，夹持长度也增大。但当伸长率越靠近3%(譬如2.3%和2.8%)，伸长率对夹持长度的影响越来越小，即两者夹持长度越来越接近。

为了使那些比较大的输入仍落在传递函数梯度大的地方，提高神经网络的辨识精度，输入样本要进行归一化处理，即使得各个输入样本数据都落在0至1的区间内。输入样本的归一化公式表示如下所示：

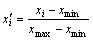                            (10)

式中：x_min和x_max分别为第i个输入样本x_i的最小值与最大值。

3.3  网络训练

网络训练过程即为学习过程，信号由输入层经隐藏层向输出层传递，若输出信号不满足期望值，则将实际输出与期望值的误差信号沿着逆向逐层返回，并以此作为修改各层网络权值和阈值的依据，直至网络输出误差达到预先设定的学习误差为止。而学习速率决定着权值和阈值的修正量，学习速率过大，将导致训练过程产生振荡或发散；学习速率过小，收敛性容易得到保证，但训练时间长，收敛速度慢。因此，学习速率一般选取0至1之间的数，本文作者选择学习速率为l_r=0.01。

同样，初始权值和阈值也在0至1区间上随机产生，若学习误差确定为1.0×10^-5后，将表3的16个样本输入网络，选用具有很快的收敛速度的LM算法对权值和阈值进行训练，网络在43258步收敛到要求精度，如图6所示。最后利用MATLAB函数对上述网络进行仿真与计算，实现输入和输出之间的非线性映射，即

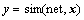                                   (11)

式中：net为训练后的神经网络；sim为MATLAB的仿真函数；x=[x₁, x₂]^T为输入变量；y为输出变量，即板材的最小夹持长度L_min。

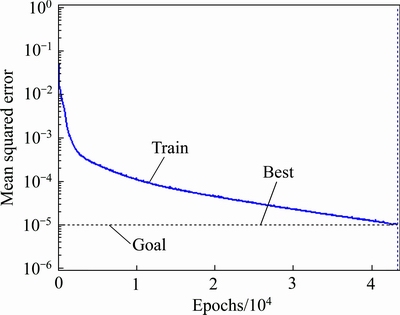
图6  网络训练收敛过程

Fig. 6  Convergence of network training

表4  样本测试数据输出值与有限元计算结果比较

Table 4  Comparison of predicted results with simulated values

利用式(11)预测板材厚度和伸长率对最小夹持长度的影响，并将预测值与仿真值对比，如表4所示。由此可见，测试样本的网络输出值与有限元计算结果之间的误差不超过5%。

4  结论

1) 通过将预拉伸看做夹钳下压和夹钳拉伸的两个有机统一过程，研究了本构模型、失效准则、边界条件等预拉伸过程有限元仿真的关键技术。

2) 提出了夹钳下压时的极限下压量、夹钳拉伸时的滑移因子两个概念，建立了铝合金板材压缩和拉伸的有限元分析方法，不仅能够仿真出极限下压量时一定伸长率的预拉伸过程，而且还能够判断出铝板材的滑移性。

3) 依据板材的滑移性，提出了最小夹持长度的反向步长递减算法，其核心相邻两次拉伸时滑移因子的异同，直至当前步长在给定阈值范围之内，即可获得最佳夹持长度(由于夹钳宽度一般大于板材宽度，故最小夹持长度获取后，即可获得最小夹持区)。

4) 借助神经网络的非线性映射能力，通过有限组的训练样本，构建了由板材厚度、伸长率预测最小夹持长度的数学模型。该神经网络的预测结果非常合理，对生产实际具有较好的指导意义。

REFERENCES

[1] 韩念梅, 张新明, 刘胜胆, 宋丰轩. 预拉伸对 7050 铝合金断裂韧性的影响[J]. 中国有色金属学报, 2010, 20(11): 2088-2093.

HAN Nian-mei, ZHANG Xin-ming, LIU Sheng-dan, SONG Feng-xuan. Effect of prestretching on fracture toughness of 7050 aluminum alloy[J]. The Chinese Journal of Nonferrous Metals, 2010, 20(11): 2088-2093.

[2] 秦国华, 林 锋, 左敦稳. 基于材料非均匀性的铝厚板预拉伸残余应力的预测方法[J]. 中国有色金属学报, 2015, 25(3): 1-8.

QIN Guo-hua, LIN Feng, ZUO Dun-wen. Prediction approach to residual stresses distribution in aluminum alloy pre-stretched thick plate based on material non-uniformity[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(3): 1-8.

[3] 林高用. 高性能7x75系铝合金厚板加工技术相关基础研究[M]. 长沙: 中南大学, 2006.

LIN Gao-yong. Effect of pre-ageing temperature and retrogression heating rate on microstructure and properties of 7055 aluminium alloy[M]. Changsha: Central South University, 2006.

[4] 王祝堂. 对当前铝厚板热轧与大挤压型材项目投资热的分析[J]. 世界有色金属, 2012(1): 58-60.

WANG Zhu-tang. Analysis of current investment boom for hot rolling and large extrusion of aluminum alloy thick plates[J]. World Nonferrous Metals, 2012(1): 58-60.

[5] ZHANG S Y, WU Y X, GONG H. A modeling of residual stress in stretched aluminum alloy plate [J]. Journal of Materials Processing Technology, 2012, 212(11): 2463-2473.

[6] 王中秋. 航空整体结构件加工变形滚压校正理论及方法研究[D]. 济南: 山东大学, 2009.

WANG Zhong-qiu. Study on theory and approach for correcting aerospace monolithic component due to machining distortion using rolling method[D]. Jinan: Shandong University, 2009.

[7] 宋 寒, 杨吟飞, 陈 波, 郑晓伟. 7055-T7751铝合金预拉伸板内部残余应力分布评估[J]. 机械制造与自动化, 2016, 45(1): 18-21.

SONG Han, YANG Yin-fei, CHEN Bo, ZHENG Xiao-wei. Evaluation of residual stress in depth profile of 7055-T7751 pre-stretched aluminum alloy plate[J]. Machine Building & Automation, 2016, 45(1): 18-21.

[8] 郑 林, 车路长, 张 津, 张鹏程, 何长光, 彭正坤, 肖 勇, 封先河, 朱 蕾. 预拉伸厚铝板内部残余应力与晶粒取向均匀性的研究[J]. 精密成形工程, 2014, 6(5): 50-58.

ZHANG Lin, CHE Lu-chang, ZHANG Jin, ZHANG Peng-cheng, HE Chang-guang, PENG Zheng-kun, XIAO Yong, FENG Xian-he, ZHU Lei. Internal residual stress and texture homogenization in pre-stretched aluminum alloy plate[J]. Journal of Netshape Forming Engineering, 2014, 6(5): 50-58.

[9] 龚 海, 吴运新, 廖 凯. 预拉伸对7075铝合金厚板残余应力分布的影响[J]. 材料热处理学报, 2009, 30(6): 202-205.

GONG Hai, WU Yun-xin, LIAO Kai. Influence of pre-stretching on residual stress distribution in 7075 aluminum alloy thick plates[J]. Transactions of Materials and Heat Treatment, 2009, 30(6): 202-205.

[10] 袁望姣, 吴运新. 基于预拉伸工艺的铝合金厚板残余应力消除机理[J]. 中南大学学报(自然科学版), 2011, 42(8): 2303-2308.

YUAN Wang-jiao, WU Yun-xin. Mechanics about eliminating residual stress of aluminum alloy thicken-plates based on pre-stretching technology[J]. Journal of Central South University (Science and Technology), 2011, 42(8): 2303-2308.

[11] 朱才朝, 罗家元, 李大峰, 丁华峰, 钟 渝. 7075铝合金板预拉伸工艺研究[J]. 机械工程学报, 2011, 47(24): 57-62.

ZHU Cai-chao, LUO Jia-yuan, LI Da-feng, DING Hua-feng, ZHONG Yu. Numerical simulation and experimental investigation of the aluminum alloy quenching process by considering the flow stress characteristic[J]. Journal of Mechanical Engineering, 2011, 47(24): 57-62.

[12] TANNER D A, ROBINSON J S. Modelling stress reduction techniques of cold compression and stretching in wrought aluminum alloy products[J]. Finite Elements in Analysis and Design, 2003, 39(5/6): 369-386.

[13] 朱才朝, 罗家元, 钟 渝. 考虑夹持影响的铝合金拉伸模拟及试验[J]. 材料科学与工艺, 2011, 19(6): 16-20.

ZHU Cai-chao, LUO Jia-yuan, ZHONG Yu. Stretching simulation and experiment of aluminum alloy sheet with clamping[J]. Materials Science & Technology, 2011, 19(6): 16-20.

[14] 李淑明, 刘贤锋, 胡永会. 铝合金厚板淬火-预拉伸残余应力的有限元仿真[J]. 热加工工艺, 2012, 41(14): 209-211.

LI Shu-ming, LIU Xian-feng, HU Yong-hui. FEM simulation of quenching-prestretching residual stress for aluminum alloy thick plate[J]. Hot Working Technology, 2012, 41(14): 209-211.

[15] 辜蕾钢, 汪凌云, 刘晓川. 铝合金厚板预拉伸过程分析[J]. 轻合金加工技术, 2014, 32(4): 27-29.

GU Lei-gang, WANG Ling-yun, LIU Xiao-chuan. Prestretch process analysis of aluminum alloy thick plates[J]. Light Alloy Fabrication Technology, 2014, 32(4): 27-29.

[16] 董辉跃. 航空整体结构件加工过程的数值仿真[D]. 杭州: 浙江大学, 2004.

Dong Hui-yue. Machining process simulation of aerospace monolithic component[D]. Hangzhou: Zhejiang University, 2004.

[17] 秦国华, 王华敏, 叶海潮, 吴竹溪. 基于力的存在性与可行性的夹紧力变向增量递减规划算法[J]. 机械工程学报, 2016, 52(11): 72-79.

QIN Guo-hua, WANG Hua-min, YE Hai-chao, WU Zhu-xi. A planning algorithm of clamping forces for workpiece fixturing scheme based on existence and feasibility of forces[J]. Journal of Mechanical Engineering, 2016, 52(11): 72-79.

[18] 秦国华, 孙 烁, 王华敏, 左敦稳, 吴铁军, 鲁宇明. 基于工件稳定性的全区域夹紧力变向迭代规划算法[J]. 兵工学报, 2016, 37(9): 1700-1707.

QIN Guo-hua, SUN Shuo, WANG Hua-min, ZUO Dun-wen, WU Tie-jun, LU Yu-ming. A reverse direction iterative planning algorithm of clamping forces in entire region based on workpiece stability[J]. Acta Armamentarii, 2016, 37(9): 1700-1707.

[19] ANDONIE R. The psychological limits of neural computation[C]// Dealing with Complexity: A Neural Network Approach. KARNY M, WARWICK K, KURKOVA V. London: Springer-Verlag, 1997: 252-263.

[20] 张园园, 吴运新, 李丽敏, 张明容. 7075铝合金预拉伸板淬火后残余应力的有限元模拟[J]. 热加工工艺, 2008, 37(14): 88-91.

ZHANG Yuan-yuan, WU Yun-xin, LI Li-min, ZHANG Ming-rong. Finite element simulation of residual stress in pre-stretching thick-plates of 7075 aluminum alloy after quenching[J]. Hot Working Technology, 2008, 37(14): 88-91.

Holding area prediction of aluminum alloy thick plate for pre-stretching processes based on diminishing step algorithm with opposite direction

QIN Guo-hua, WANG Zhi-gang, LIN Feng, YE Hai-chao

(School of Aeronautical Manufacturing Engineering, Nanchang Hangkong University, Nanchang 330063, China)

Abstract: Pre-stretching is the main method to eliminate the residual stress in aluminum alloy plate. But the holding of stretching machine clampers on the two ends of the plate can affect the cutting volume and yield of prestretched plate, as well as the elimination of residual stresses in end of plate. Therefore, by investigating the crucial technologies for the pre-stretching of aluminum alloy plate, including the constitutive model, boundary condition, failure criterion, as so on, the finite element analysis method is established for the limited pressure and slip factor. And then, while the function of initial holding length is constructed properly, the sum of the current holding length with a certain step can be taken as the next holding length. Thus, when the slip factors between the current holding length and the last one are calculated, the difference of the two can be judged. If the two is the same, the next holding length increases with the same step along the same direction. Otherwise, the next holding length decreases with the diminishing step along the opposite direction. The difference of the slip factor of current holding length with last holding length is iteratively validated until the absolute value of the step is not more than the given threshold value. Thus, the diminishing step algorithm with opposite direction of the minimum holding length can be suggested to obtain the neural network training samples with the thickness of the plate and the stretch rate as input. With the nonlinear mapping of neural network, a neural network prediction model of the minimum holding length is established by the finite groups of training samples. By comparing the predicted value with the corresponding finite element simulation, it shows that the prediction error is less than 5%. Obviously, the proposed diminishing step algorithm with opposite direction is reasonable to holding area prediction of aluminum alloy thick plate for pre-stretching processes.

Key words: pre-stretching of aluminum alloy thick plate; limited pressure; slip factor; minimum holding length; diminishing step algorithm with opposite direction

Foundation item: Projects(51465045, 51165039) supported by the National Natural Science Foundation of China; Project(20161BAB206114) supported by the Natural Science Foundation of Jiangxi Province, China

Received date: 2016-08-15; Accepted date: 2017-03-20

Corresponding author: QIN Guo-hua; Tel: +86-791-83863038; E-mail: qghwzx@126.com

(编辑  王  超)

基金项目：国家自然科学基金资助项目(51465045，51165039)；江西省自然科学基金资助项目(20161BAB206114)

收稿日期：2016-08-15；修订日期：2017-03-20

通信作者：秦国华，教授，博士；电话：0791-83863038；E-mail: qghwzx@126.com