网络首发时间: 2017-05-04 11:06

稀有金属 2018,42(06),634-639 DOI:10.13373/j.cnki.cjrm.xy17030055

拉速对12英寸单晶硅点缺陷分布影响的动态模拟仿真研究

年夫雪 黄嘉丽 邓康 任忠鸣 吴亮

摘 要：

半导体单晶生长过程中伴随大量的空穴性和间隙性本征点缺陷, 这些本征缺陷在单晶生长过程中随着晶体温度的降低不断复合或湮灭形成纳米级空洞型或位错、层错等缺陷, 会对硅片质量及后续的器件性能产生严重影响。利用计算机模拟仿真技术对12英寸半导体直拉单晶硅生长过程的传热及点缺陷进行了动态模拟仿真计算。动态仿真计算过程中分别采用了恒定及连续变化的拉速, 以研究单晶直拉速度对点缺陷分布的影响。研究结果表明, 生长速度较快时, 晶体内部主要以空穴性点缺陷为主;当生长速度逐步降低, 晶体内部空穴性缺陷区域逐渐缩小;通过合适的拉速控制及V/G理论, 使用点缺陷动态模拟仿真计算可为生长特定点缺陷分布甚至无点缺陷硅单晶工艺提供有效依据。

关键词：

12英寸单晶硅;动态模拟;点缺陷;

中图分类号： O77;TQ127.2

作者简介：年夫雪 (1989-) , 女, 安徽蚌埠人, 硕士, 研究方向:大尺寸直拉硅单晶模拟仿真技术;E-mail:15026919881@163.com;;吴亮, 教授;电话:021-56331694;E-mail:lwu@shu.edu.cn;

收稿日期：2017-03-26

基金：国家自然科学基金项目 (U1560202, 51401116);上海市科委基金项目 (13DZ1108200, 13521101102) 资助;

Pulling Rate on Point-Defect Distribution in 12-Inch Silicon Single Crystal by Dynamical Simulations

Nian Fuxue Huang Jiali Deng Kang Ren Zhongming Wu Liang

State Key Laboratory of Advanced Special Steel & Shanghai Key Laboratory of Advanced Ferrometallurgy, School of Materials Science and Engineering, Shanghai University

Abstract：

During Czochralski silicon single crystal growth, a large amount of native point defects precipitated at melt/crystal interface due to defect supersaturation. With the decrease of crystal temperature, nanoscale micro-void and dislocation would grow through recombination or annihilation. All these defects had a serious impact on wafer quality and subsequent device performance. Global modeling and dynamical simulations of heat transfer and point defects for Czochralski 12-inch silicon single crystal growth were performed.The numerical simulation results showed that the core of growing crystal was dominated by vacancies when the growth rate was high, and the diameter of vacancy-dominated core decreased when the growth rate was gradually reduced. At enough low growth rate the whole core of growing crystal became interstitial-dominated. Point-defect dynamical simulations could provide an efficient way to grow silicon single crystals with specific point-defect distribution or even defect-free crystals through appropriate control of pulling rate.

Keyword：

12-inch silicon single crystal; dynamical simulation; point defects;

Received： 2017-03-26

超大规模、超高速集成电路的迅速发展对大尺寸、高质量的单晶硅片需求日益苛刻。直拉法 (Czochralski) 作为生长单晶硅常用的方法之一, 其优点是可以生长出大直径、高质量半导体级与太阳能级单晶硅。然而直拉单晶硅生长过程中由于温度变化、熔体对流、热场材质等会产生各种杂质与微缺陷。典型的微缺陷包括位错、层错与空洞型缺陷 (void) 。空洞型缺陷主要是原子级空穴性本征点缺陷的聚集并长大形成, 其典型尺寸在100 nm上下^[1]。位错等缺陷主要由间隙性点缺陷的聚集并长大形成, 其典型尺寸甚至可以到微米级。空洞型缺陷使得集成电路栅氧化层完整性 (GOI) 降低, 从而影响半导体器件的电学性能^[2]。

硅中的空位及间隙本征点缺陷饱和浓度与温度强烈相关。随着硅液在温度较低的固/液生长界面聚集, 空位及间隙性点缺陷饱和浓度下降, 大量空位及间隙性缺陷由于处于过饱和状态迅速在固/液界面形成并扩散至晶体内部。因此, 大量本征点缺陷在固/液界面形成并进入晶体内的过程不可避免与控制。各种杂质也通过影响硅中点缺陷的产生、扩散、复合, 从而影响点缺陷的平衡浓度, 最终影响硅中微缺陷的形成^[3,4,5,6]。

在过去的二三十年中, 很多研究学者在点缺陷分布与控制方面做了许多有意义的研究工作^{[7,8,9,10,11]}。Voronkov提出了缺陷控制V/G理论, 指出晶体生长时最终占主导地位的点缺陷类型由V/G决定 (V为固/液界面法向生长速度, G为固/液界面法向温度梯度) 。当V/G大于临界值时, 晶体内的缺陷类型以空位型缺陷为主;当V/G小于临界值时, 生长出的晶体内自间隙型缺陷占主导^[12]。对于特定的温度场, 固/液界面法向温度梯度G通常仅能在较小的范围内变化, 因此根据这一理论可以通过控制晶体生长速度来控制单晶硅中的缺陷类型。Dornberger和Ammon等^[13]通过实验与数值模拟结合的方法进一步证实了Voronkov的缺陷控制理论, 并提出当V/G= (V/G) _crit=0.13 mm²·min^-1·K^-1时氧化诱生层错环 (OSF) 消失, 当V/G> (V/G) _crit时晶体中的缺陷以空位型缺陷为主, 当V/G< (V/G) _crit时, 晶体中的缺陷以自间隙相关的缺陷为主。Sinno等通过使用数值计算与点缺陷行为的渐进分析方法相结合进一步解释了该理论, 并提出了完整的点缺陷模型, 分析并解释了氧化诱生层错环的形成、发展及其与V/G的关系^[14]。

过去的研究表明, 点缺陷主要通过扩散进入晶体, 因此晶体中的点缺陷分布与晶体生长过程的热历史强烈相关, 准稳态仿真计算通常不再适用^[15]。为此, 本文在上述研究的基础上, 利用动态数值模拟仿真技术首次研究了12英寸直拉单晶硅在恒定拉速及变拉速条件下点缺陷分布规律, 为研究给定热场及相关工艺条件下生长特征缺陷分布甚至无缺陷晶体奠定工艺基础。

1 仿真过程

1.1 数学模型

本文模拟软件采用的是晶体生长专业软件FEMAG-CZ。该软件以实际炉体结构及晶体生长工艺参数为依据, 采用有限元法对晶体生长过程中的传热和传质过程进行全局性数值模拟。计算模型耦合了单晶生长炉内所有结构单元及其相应的传热方式, 从而可以精确预测整个生长炉内的全局温度分布、固/液界面的形状、熔体/气流的流动, 并能对晶体生长过程的各种杂质及掺杂元素、晶体生长过程的热应力、晶体生长点缺陷等进行计算与分析。该软件不仅可以对单晶硅生长过程的全局温度场进行准稳态模拟仿真计算, 还可以对各种点缺陷分布进行动态模拟仿真计算, 解决准稳态计算在缺陷分析方面的不足, 从而得到精确的点缺陷分布结果。计算所采用的能量控制方程、连续性方程、流体动量控制方程、固/液界面控制方程等基本控制方程可参考文献[16]。本软件采用的点缺陷控制方程及模型参数如下^[17]:

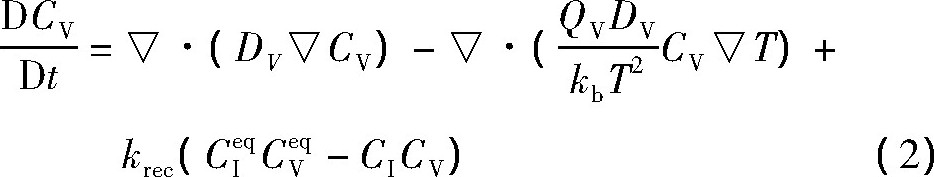
式中下标I和V分别代表自间隙与空位, t为时间, C_I, C_V分别代表自间隙与空位浓度, C_I^eq, C_V^eq分别代表自间隙与空位的平衡浓度, D_I, D_V分别为自间隙与空位的扩散系数, Q_I, Q_V分别为自间隙与空位热扩散激活焓;k_rec为动力学重组因子, k_b代表玻尔兹曼常数, T为温度, r为热扩散因子;H_I^m与H_V^m分别代表自间隙与空位的迁移焓;G_I^f, G_V^f分别为形成自间隙与空位的吉布斯自由能, H_I^f, H_V^f分别为自间隙与空位形成焓, S_I^f, S_V^f分别表示自间隙与空位形成熵。上述点缺陷控制方程在S-D模型 (Sinno与Dornberger建立的点缺陷控制模型) 的基础上充分考虑Q_I与Q_V对热传递及点缺陷扩散的影响, 其他参数与S-D模型保持一致。

1.2 仿真工艺与过程分析

本文热场结构采用适用于12英寸直拉硅单晶生长的热场, 其晶体生长工艺条件如下:总投料量为400 kg, 晶体转速为-10 r·min^-1, 坩埚转速为5 r·min^-1。众所周知, 点缺陷浓度与分布受晶体生长过程的热历史影响, 准稳态计算将不再适用, 因此, 本文模拟计算采用了FEMAG-CZ动态模拟仿真技术并使用网格变形工具, 对整个晶体生长过程的传热与传质进行全局性模拟计算。晶体总长度设定为1265 mm, 动态计算过程贯穿晶体等径生长过程。为研究拉速对点缺陷浓度与分布的影响, 动态计算晶体拉速分别设定为恒定拉速与拉速连续变化两个工艺过程 (两者拉速随晶体长度的变化见图1) , 其中恒定拉速工艺条件下拉速设定为0.45 mm·min^-1, 而变拉速条件下拉速从晶体长度170 mm时的0.45 mm·min^-1均匀下降至800 mm时的0.20 mm·min^-1, 再均匀提高至1265 mm时的0.345 mm·min^-1。本文重点研究这两种工艺条件下晶体中点缺陷浓度及分布变化规律, 为研究给定热场在相关工艺条件下生长特定缺陷分布甚至无缺陷晶体奠定工艺基础。表1为本文模拟过程中点缺陷模型计算参数的取值。

图1 拉速随晶体长度变化示意图Fig.1 Variation of pulling rates with respect to crystal length

表1 点缺陷模型计算参数Table 1 Point-defect modeling parameters  下载原图

表1 点缺陷模型计算参数Table 1 Point-defect modeling parameters

2 结果与讨论

2.1 恒定拉速与变拉速对温度场分布的影响

在晶体生长过程中, 随着晶体长度不断增加, 坩埚内熔体逐渐减少, 整体热场的温度分布将产生变化。如图2所示为两种拉速条件下, 晶体长度为1265 mm时熔体与晶体中的温度分布。从图2中可以清楚地看到, 两种拉速条件下熔体与晶体中的温度分布基本一致, 表明设定的两种拉速的变化对熔体与晶体中温度分布的影响不大。

图2 晶体长度为1265 mm, 两种拉速条件下熔体与晶体中的温度分布Fig.2Comparison of temperature distribution in melt and crystal at crystal length 1265 mm under constant and variable pull rates

2.2 恒定拉速与变拉速对晶体中点缺陷分布的影响

图3为晶体长度为800 mm, 两种拉速条件下晶体内点缺陷分布图, C_I-C_V代表自间隙与空位浓度差。从图3中可以看出, 以恒定拉速0.45 mm·min^-1生长的晶体中, 沿半径方向, 点缺陷的分布以零等值线作为分界线, 呈现出晶体内侧以空位型点缺陷为主, 外侧以自间隙型点缺陷为主的规律, 且随着晶体长度增加点缺陷分布基本保持这种规律。而变拉速条件下, 随着晶体长度的增加, 点缺陷分布沿半径方向发生了变化:当晶体长度小于280 mm时, 未出现零等值线, 即点缺陷在半径方向上全部为自间隙型缺陷为主;当晶体长度大于280 mm时, 出现一条较短的零等值线, 呈现出内侧空位型缺陷为主, 外侧自间隙型缺陷为主的特征分布。上述结果表明随着拉速的降低, 以自间隙为主的点缺陷浓度增大, 以空位为主的点缺陷浓度减小, 自间隙为主的点缺陷逐渐占优势。

图4为晶体长度为1265 mm时, 两种拉速条件下晶体中点缺陷分布图。从图4可以看到:恒拉速条件下晶体中点缺陷分布规律与上述基本相同;而变拉速条件下, 晶体靠近两端的位置各出现一条较短的零等值线, 而晶体中部很长一段晶体呈现出以自间隙缺陷为主的点缺陷浓度分布。上述结果表明随着拉速的降低, 晶体中以自间隙为主的点缺陷逐渐占优势, 而随着拉速的逐渐增大, 晶体中以自间隙为主的点缺陷浓度减小, 以空位为主的点缺陷逐渐占优势。

图3 晶体长度为800 mm, 两种拉速条件下晶体中自间隙与空位缺陷分布图Fig.3 Distribution of self-interstitials and vacancies in crystal at crystal length 800 mm

图4 晶体长度为1265 mm, 两种拉速条件下晶体中自间隙与空位分布图Fig.4 Distribution of self-interstitials and vacancies in crystal at crystal length 800 mm

为进一步直观分析拉速对点缺陷分布的影响, 选取了晶体生长长度为1265 mm时两种拉速条件下自晶体顶部起800 mm高度单晶剖面点缺陷分布示意图 (图5) 。通过图5可以清楚地看到, 常拉速下该剖面上自间隙缺陷占优势的区域占64%, 空位型点缺陷占优势的区域占36%;变拉速下自间隙缺陷占优势的区域占比高达97.6%, 而空位占优势的区域仅占2.4%。通过图1可以知道, 变拉速情况下该剖面对应的晶体拉速为0.20mm·min^-1, 因此, 当生长速度较快时, 晶体心部主要以空穴性点缺陷为主, 外侧以自间隙型缺陷为主;当生长速度逐步降低, 晶体内部逐步从空穴性缺陷为主过渡至间隙性缺陷为主。

图5 晶体长度为1265 mm时, 两种拉速条件下自晶体顶部800 mm单晶剖面点缺陷分布示意图Fig.5 Sectional view (800 mm from crystal top) of CI-CV distribution at crystal length 1265 mm

2.3 结果分析与讨论

图6所示为本文所研究的变拉速条件下点缺陷分布图与文献[17]研究报道的4英寸单晶硅在变拉速条件下生长所得到的轴向切面缺陷腐蚀图, 图6 (b) 中亮色区域代表空位型缺陷, 暗色区域代表自间隙型缺陷。从图6可以清楚地看到, 在相似的拉速条件下, 本文所得到的点缺陷分布与图6 (b) 中实验所得到的微缺陷分布及其趋势具有高度一致性。

图6 晶体长度1265 mm, 变拉速下分布;4英寸单晶硅经轴向切割、热处理和抛光腐蚀后缺陷形貌Fig.6Distribution of CI-CVat crystal length 1265 mm with variable pulling rate (a) ;Defect morphologies after heat treatment and etching for a 4-inch silicon single crystal under variable pulling rate (b)

基于前述分析得到的规律, 由此也可以推断, 当晶体拉速足够大时, 整个单晶硅剖面将全部被空穴性缺陷占据;当晶体拉速足够小时, 整个单晶硅剖面将全部为自间隙性缺陷所占据;在中等拉速条件下, 单晶剖面中心区域通常以空穴型缺陷为主, 而空穴型缺陷区域外围通常被自间隙型缺陷所包围。随着晶体生长在高温下的进一步进行, 空穴型及自间隙型缺陷边界附近通常由于高温扩散导致空位与自间隙相两种点缺陷会发生大量的复合与湮灭, 使得整体点缺陷浓度大大降低, 从而得到少缺陷甚至无缺陷的晶体。

研究表明, 直拉单晶硅中点缺陷的分布由V/G决定。晶体生长时, 空位与自间隙原子在温度较低的固/液界面处由于处于过饱和状态而不断产生, 并沿晶体轴向方向随着温度的降低而不断复合、湮灭, 导致点缺陷从固/液界面向晶体内部轴向扩散;同时, 由于晶体径向空穴型及自间隙型缺陷浓度的差别, 空穴型缺陷及自间隙型缺陷也会沿相反方向进行自扩散;此外, 晶体以生长速率V脱离固/液界面向上运动, 也会造成点缺陷的轴向运输。因此, 晶体生长时最终占主导地位的点缺陷类型由V/G决定。

如图7与8分别表示两种拉速条件下不同长晶阶段固液界面温度梯度及固液界面V/G图。从图7, 8可以看出:晶体中心部位温度梯度最低, 并沿半径方向逐渐增大, 因此晶体中心部位V/G值通常较大, 而外侧V/G值相对较小。根据晶体缺陷V/G理论, 中心部位点缺陷以空位型缺陷为主, 而边缘处以自间隙型缺陷为主。通过改变拉速, 使得V/G值发生相应变化, 因此合理地控制拉速能够得到具有特定缺陷分布特征的晶体。

图7 不同长晶阶段恒定拉速与变拉速固液界面温度梯度Fig.7 Thermal gradientsat melt/crystal interface under differ-ent pulling rates and crystal lengths

图8 恒定拉速与变拉速下不同长晶阶段的V/G Fig.8 V/G along melt/crystal interface under different pulling rates and crystal lengths

3 结论

利用计算机模拟仿真技术对12英寸半导体直拉单晶硅生长过程的传热及点缺陷进行了动态模拟仿真计算。动态仿真计算过程中分别采用了恒定及连续变化的拉速, 以研究单晶直拉速度对点缺陷分布的影响。研究结果表明, 生长速度较大时, 晶体内部主要以空穴性点缺陷为主;当生长速度逐步降低, 晶体内部空穴性缺陷区域逐渐缩小;当单晶生长拉速足够大或足够小时, 可分别生长出完全为空穴型缺陷或自间隙型缺陷的硅单晶。通过合适的拉速控制及V/G理论, 使用点缺陷动态模拟仿真计算可为生长特定点缺陷分布甚至无点缺陷硅单晶工艺提供有效依据。

参考文献

[1] Ueki T, Itsumi M, Takeda T.Octahedral void defects observed in the bulk of Czochralski silicon[J].Applied Physics Letters, 1997, 70 (10) :1248.

[2] Sinno T, Dornberger E, Ammon W von, Brown R A, Dupret F.Defect engineering of Czochralski singlecrystal silicon[J].Materials Science and Engineering, 2000, 28 (5-6) :149.

[3] Falster R, Voronkov V V.The engineering of intrinsic point defects in silicon wafers and crystals[J].Materials Science and Engineering, 2000, B73 (1-3) :87.

[4] Voronkov V V, Falster R.Vacancy-type microdefect formation in Czochralski silicon[J].Journal of Crystal Growth, 1998, 194 (1) :76.

[5] Han H J, Zhou Q G, Dai X L.Effects of nitrogen on oxidation induced stacking faults in 300 mm CZ silicon[J].Chinese Journal of Rare Metals, 2009, 33 (2) :223. (韩海建, 周旗钢, 戴小林.300 mm直拉单晶硅中的氮元素对氧化诱生层错的影响[J].稀有金属, 2009, 33 (2) :223.)

[6] Feng Y K, Li N, Ren L, Ren B Y.Defects and minority lifetime of Ga doped CZ-Si single crystal with heat treatment[J].Chinese Journal of Rare Metals, 2016, 40 (6) :626. (丰云恺, 李宁, 任丽, 任丙彦.热处理对掺镓直拉单晶硅中缺陷及少子寿命的影响[J].稀有金属, 2016, 40 (6) :626.)

[7] Falster R, Voronkov V V, Quast F.On the properties of the intrinsic point defectsin silicon:a perspective from crystal growth and wafer processing[J].Physica Status Solidi, 2000, 222 (1) :219.

[8] Dupret F, Nicodeme P, Ryckmans, Y, Wouters P, Crochet M J.Global modelling of heat transfer in crystal growth furnaces[J].International Journal of Heat and Mass Transfer, 1990, 33 (9) :1849.

[9] Tan T Y, Gosele U.Point defects, diffusion processes, and swirl defect formation in silicon[J].Applied Physics A, 1985, 37 (1) :1.

[10] Ammon W von, Dornberger E, Oelkrug H, Weidner H.The dependence of bulk defects on the axial temperature gradient of silicon crystals during Czochralski growth[J].Journal of Crystal Growth, 1995, 151 (3-4) :273.

[11] Wijaranakula W.A real-time simulation of point defect reactions near the solid and melt interface of a 200 mm diameter Czochralski silicon crystal[J].Journal of the Electrochemical Society, 1993, 140 (11) :3306.

[12] Voronkov V V.The mechanism of swirl defects formation in silicon[J].Journal of Crystal Growth, 1982, 59 (3) :625.

[13] Dornberger E, Ammon W von.The dependence of ringlike distributed stacking faults on the axial temperature gradient of growing Czochralski silicon crystals[J].Journal of the Electrochemical Society, 1996, 143 (5) :1648.

[14] Sinno T, Brown R A, Ammon W von, Dornberger E.Point defect dynamics and the oxidation-induced stackingfault ring in Czochralski-grown silicon crystals[J].Journal of the Electrochemical Society, 1998, 145 (1) :302.

[15] Van Goethem N, de Potter A, Van den Bogaert N, Dupret F.Dynamic prediction of point defects in Czochralski silicon growth.An attempt to reconcile experimental defect diffusion coefficients with the V=G criterion[J].Journal of Physics and Chemistry of Solids, 2008, 69 (2-3) :320.

[16] Nian F X, Deng X L, Deng K, Ren Z M, Wu L.3D numerical simulation of Czochralski 18-Inch silicon ingot growth under horizontal magnetic field[J].Chinese Journal of Rare Metals, 2017, 41 (3) :297. (年夫雪, 邓先亮, 邓康, 任忠鸣, 吴亮.水平磁场下18英寸直拉硅单晶生长工艺的三维数值模拟[J].稀有金属, 2017, 41 (3) :297.)

[17] Dornberger E.Prediction of OSF Ring Dynamics and Grown-in Voids in Czochralski Silicon Crystals[D].Louvain:Catholic University of Louvain, 1997.118.