Chaotic system and QR factorization based robust digital image watermarking algorithm
来源期刊:中南大学学报(英文版)2011年第1期
论文作者:宋伟 侯建军 李赵红 黄亮
文章页码:116 - 124
Key words:digital watermarking; QR factorization; pseudorandom circular chain; logistic mapping
Abstract: In order to protect copyright of digital images, a new robust digital image watermarking algorithm based on chaotic system and QR factorization was proposed. The host images were firstly divided into blocks with same size, then QR factorization was performed on each block. Pseudorandom circular chain (PCC) generated by logistic mapping (LM) was applied to select the embedding blocks for enhancing the security of the scheme. The first column coefficients in Q matrix of chosen blocks were modified to embed watermarks without causing noticeable artifacts. Watermark extraction procedure was performed without the original cover image. The experimental results demonstrate that the watermarked images have good visual quality and this scheme is better than the existing techniques, especially when the image is attacked by cropping, noise pollution and so on. Analysis and discussion on robustness and security issues were also presented.
J. Cent. South Univ. Technol. (2011) 18: 116-124
DOI: 10.1007/s11771-011-0668-8
![]()
SONG Wei(宋伟)1, 2, HOU Jian-jun(侯建军) 1, LI Zhao-hong(李赵红) 1, HUANG Liang(黄亮) 1
1. School of Electronics and Information Engineering, Beijing Jiaotong University, Beijing 100044, China;
2. School of Information Engineering, Minzu University of China, Beijing 100081, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract: In order to protect copyright of digital images, a new robust digital image watermarking algorithm based on chaotic system and QR factorization was proposed. The host images were firstly divided into blocks with same size, then QR factorization was performed on each block. Pseudorandom circular chain (PCC) generated by logistic mapping (LM) was applied to select the embedding blocks for enhancing the security of the scheme. The first column coefficients in Q matrix of chosen blocks were modified to embed watermarks without causing noticeable artifacts. Watermark extraction procedure was performed without the original cover image. The experimental results demonstrate that the watermarked images have good visual quality and this scheme is better than the existing techniques, especially when the image is attacked by cropping, noise pollution and so on. Analysis and discussion on robustness and security issues were also presented.
Key words: digital watermarking; QR factorization; pseudorandom circular chain; logistic mapping
1 Introduction
The rapid growth of Internet have changed our society and daily lives. However, the protection of intellectual property right (IPR) of digital multimedia becomes a crucial problem. As an effective technique, digital watermarking has been proposed. And it can be classified into fragile digital watermark technique, semi-fragile digital watermark technique, and robust digital watermark technique.
In the fragile watermark algorithms [1-4], sensitive characteristics of host images are often used to embed watermarks, such as prominent intensity pixel value of image blocks and least significant bit (LSB). They are so sensitive to the sorts of operations where these algorithms are used to verify the integrity of digital images.
The semi-fragile watermark algorithms [5-9] are robust to some distortions, but fragile to other operations. For example, ZHANG and YANG [8] used JPEG invariant characteristic to embed watermarks by qualifying DCT coefficients. This scheme can resist JPEG compression, but it is fragile to other attacks. Semi-fragile watermark schemes are used to authenticate the protected images even these images suffer from some attacks.
The main purpose of the robust the digital watermarking techniques [10-18] is the ownership authentication or the copyright protection. These algorithms can resist attacks and extract watermarks successfully from the distorted images. There are two main approaches: schemes in spatial domain [10-11], and schemes in frequency domain [12-18]. In spatial domain, watermarks are embedded by modifying the pixel value directly. In the frequency domain, the protected images must first be transformed into frequency domain by using a frequency-oriented mechanism, such as discrete Fourier transforms (DFT) [12], discrete cosine transforms (DCT) [13], and discrete wavelet transforms (DWT) [14-18], or other techniques. Some of these algorithms use human visual system (HVS) to improve the visual quality of the watermarked images, and use quantization and statistical method to enhance robustness.
In this work, the invariant characteristics of QR factorization were investigated and a novel robust digital image watermarking scheme based on chaotic system and QR factorization was proposed. QR factorization was used to embed and extract watermarks for its good performances, and logistic mapping (LM) was used to generate pseudorandom circular chain (PCC) in order to enhance the security of this scheme.
2 Basic theories
2.1 QR factorization
In QR factorization [19], the orthogonal triangular decomposition of a matrix is performed, which is defined as
A=[a1, a2, ???, an]=qr(A)=QR (1)
where Q is an orthogonal matrix (its columns are orthogonal unit vectors meaning QTQ=I) and R is an upper triangular matrix (also called right triangular matrix).
In QR factorization, the elements of first row in the upper triangular matrix is bigger than other rows, so power of the matrix is distributed averagely on top right corner. The first column of Q represents the relationship between pixels. So, Q can resist attacks for its orthogonal characteristic. And two conclusions can be gotten as follows:
1) The first row of R matrix has determined the complexity of the original matrix.
2) The coefficients in first column of Q may be modified for robust QR-based watermarking algorithm.
Here, an example is given to illustrate the relationship between the Q component coefficients. The original image and the distorted image are shown in Figs.1(a) and (b), respectively. Table 1 shows the pixel values of the original block and the corresponding luminance-enhanced block, and their Q components, respectively. From Table 1, we can see that the magnitude relationships (i.e., |-0.507 2|>|-0.490 5| and |-0.505 3|>|-0.493 0|) between the coordinates (1, 2) and (1, 3) can be preserved well even though the luminance processing is performed. The ratio of invariant symbol in each component to total number blocks is also tested when the host image is attacked by JPEG compression (Factor: 70), noise (0.03), luminance- enhancement (50%), contrast-enhancement (50%), blurring, and sharpening. In Fig.2, Ci (i=1, 2, 3, 4) represents the i-th column component. It can be observed that only the symbol in first column of Q is invariant. So, watermarks can be embedded by modifying the first column of Q.
2.2 Logistic mapping system and pseudorandom circular chain (PCC)
Logistic mapping (LM) system is a chaotic system, and it is often used in watermarking technique for its simpleness and good performance [10]. The definition is as follows:
xn+1=λxn(1-xn), λ∈[0, 4], xn∈(0, 1) (2)
where λ is the control parameter of logistic mapping system.
Pseudorandom circular chain (PCC) can be generated by logistic mapping system [4]. PCC has the following

Fig.1 Original (a) and luminance-enhanced (b) images
Table 1 Relationship of QR factorization transformed Q component coefficients between original block and its corresponding luminance-enhanced block
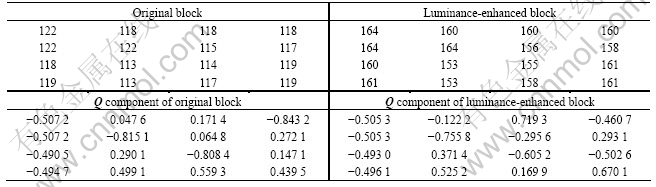

Fig.2 Ratio of invariant symbol in each column of Q component
characteristics, which meet the need of the security of the algorithm:
1) The mapping relationship in PCC is one to one, and it is non-overlapped;
2) PCC is decided by key, and different keys can generate different PCC;
3) The neighbor elements in PCC are far away from each other;
4) Because PCC is generated by chaotic system, the key space is large enough.
3 Proposed algorithm
3.1 Watermarks embedding procedure
In watermark-embedding procedure, watermark image Wp×q was embedded by modifying the first column component of Q matrix in QR factorization of selected blocks by PCC. The detail of watermark embedding procedure is described as follows.
Step 1: Host image Io with size of N×M was partitioned into non-overlap blocks with size of (N/n)× (M/m):
 (3)
(3)
Step 2: QR factorization was performed on each block:
[Q(i, j), R(i, j)]=qr(I(i, j)), (i=1, 2, ???, n; j=1, 2, …, m) (4)
where qr represents QR factorization function, I(i,j) represents the block (i, j), Q(i, j), R(i, j) stand for Q and R matrix in QR factorization of block I(i, j), respectively.
Step 3: PCC was built by key k:
PCC=f (LM (k, n×m)) (5)
Step 4: Embedding blocks were selected by PCC.
Step 5: Two-dimensional watermark image Wp×q was transformed into one-dimensional sequences: wl (l=1, 2, ???, p×q).
Step 6: Watermarks were embedded as follows:
The modification of Q component coefficients might alter the original pixel values and degraded the quality of the watermarked image. The larger the modification of Q component was, the worse the distortion of image quality was, but the stronger the robustness of the scheme was. On the other hand, the smaller modification implied better image quality and weaker robustness. Therefore, a tradeoff between robustness and quality should be selected.
Assume that watermark wi corresponded to the selected block (i, j). When wi was 1, it was embedded as follows:
?1=|Q(i, j)(2, 1)|-|Q(i, j)(3, 1)|, ?2=-?1;
if ?1≥T,
![]()
if ?2≥T,
![]()
if 0≤?1
![]()
![]()
if ![]()
![]()
![]()
When wi was 0, the first column components were modified as follows:
if ?1≥T,
![]()
if ?2≥T,
![]()
if 0≤?1
![]()
![]()
if 0≤?2
![]()
![]()
This step was repeated until all bits of watermarks were embedded.
Step 7: Inverse QR factorization was performed to reconstruct the watermarked image Iw:
![]() (6)
(6)
3.2 Watermark extraction procedure
The watermarking scheme could be categorized into blind scheme or non-blind scheme according to whether the original host image was needed in the extraction procedure or not. In this scheme, original cover image was not needed in watermark extraction procedure and the scheme was blind.
The watermark extraction was the reverse procedure of the watermark embedding, and it was described as follows.
Step 1: The tested image IW was divided into non- overlap blocks with size (N/n)×(M/m).
Step 2: QR factorization was performed on each block.
Step 3: PCC was built by key k.
Step 4: The extraction blocks were selected by PCC.
Step 5: Assuming that watermark wl corresponded to block (i, j), watermark wl was extracted as follows:
![]() (7)
(7)
This step was repeated until all bits of watermarks were extracted.
Step 6: Watermark image ![]() was reconstructed by transforming the one-dimensional into two-dimensional watermark sequences.
was reconstructed by transforming the one-dimensional into two-dimensional watermark sequences.
4 Experimental results and discussion
4.1 Experimental results
In this experiment, several simulations are performed to verify the validity of the proposed watermarking scheme. Three gray-level images with size of 512×512 named Plane, Baboon and Lena are selected as host images (Figs.3(a), (b) and (c)) and a 32×32 binary image, as shown in Fig.3(d), is taken as the watermark image. These host images are partitioned into non-overlap blocks with size of 4×4, with the key of PCC k=0.123 and the threshold T=0.42. Peak signal- noise ratio (PSNR, RPSN) is introduced to evaluate the quality difference between the embedded image and the original host images, and bit error ratio (BER, RBE) is used to evaluate the difference between the original watermark image and the extracted watermark image, which are, respectively, defined by
 (8)
(8)
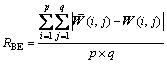 (9)
(9)
where IW, Io, M×N denote the watermarked image, the original host image, and the size of the image, respectively. And ![]() W, p×q stand for the extracted watermarks, the original watermarks, and the size of the watermarks, respectively.
W, p×q stand for the extracted watermarks, the original watermarks, and the size of the watermarks, respectively.
The watermarked images and the extracted watermark image are shown in Fig.4. It is found that PSNR among these watermarked images are greater than 40 dB. Especially, PSNR of watermarked image Lena is higher than 44 dB, which indicates that the difference between the original images and the watermarked images cannot be distinguished by human eyes. And the watermark image extracted from the watermarked image with free-attack is the same as the original watermark image because BER between the original watermark image and extracted watermark image is zero, which indicates that watermark image can be extracted correctly from the free-attack embedded images.
4.2 Robustness analysis
Robustness means the watermark image extracted from the attacked images cannot be distorted to such an extent that the watermark image is not clear enough for the ownership authentication. It is the main criterion to evaluate the effectiveness of the proposed scheme.
Some experiments including JPEG compression,

Fig.3 Original host images ((a) Plane; (b) Baboon; (c) Lena) and watermark image (d)

Fig.4 Watermarked images ((a) 42.74 dB; (b) 40.05 dB; (c) 44.43 dB) and extracted watermark image (d) (RBE=0)
noise pollution, cropping, luminance-enhancement, contrast-enhancement, sharpening, blurring and tampering are performed. For tamper attack, “Lena Tamper” is written on the face of Lena. Experiment results are shown in Fig.5. PSNR of these attacks are 37.985 3, 20.776 7, 11.270 5, 16.372 2, 28.881 1, 33.737 1, 40.512 7, and 28.111 5 dB, respectively, and BER of their corresponding extracted watermark images

Fig.5 Attacked images and corresponding extracted watermark images: (a) Sharpening (RBE=0.002 9); (b) Cropping (RBE=0.081 1); (c) Luminance (RBE=0); (d) Contrast (50%) (RBE=0); (e) Noise (3%) (RBE=0.021 5); (f) JPEG (70) (RBE=0.075 2); (g) Blurring (RBE=0.025 4); (h) Tampering (RBE=0.005 9)
are 0.075 2, 0.021 5, 0.081 1, 0, 0, 0.002 9, 0.025 4 and 0.005 9. It can be seen from Fig.5 that although attacks lead big distortion to watermarked images, the extracted watermark images have good visual quality, and BER of all extracted watermark images are lower than 0.1, and some are even zero, which can meet the need of the authentication or the annotation.
In order to test the robustness and show the advantage of the proposed scheme, normalized correlation (C) is used to compare the experimental results with the existing algorithms proposed by LI and LIANG [15] and LIN et al [16], and BER is compared with the scheme proposed by SUN et al [9]. The definition is as follows:
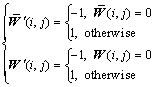 (10)
(10)
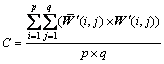 (11)
(11)
where ![]()
![]()
![]() W′(I, j)
W′(I, j)![]() (-1, 1) and p×q stand for the size of the watermarks.
(-1, 1) and p×q stand for the size of the watermarks.
The comparison results of the proposed method and the method proposed in Ref.[15] and Ref.[16] are shown in Table 2. From Table 2, it can be noted that normalized correlation values are higher than those of the other two methods when the image is attacked by sharpening and cropping, but lower than those of the scheme in Ref.[15] for its frequency domain embedding when the host image is processed by JPEG compression. However, all values of extracted watermark images are higher than those of the scheme in Ref.[16].
Table 2 Comparison of this method (RPSN=44.43 dB) and methods in Ref.[15] (RPSN=40.6 dB) and Ref.[16] (RPAN=44.25 dB)

The simulation results are also compared with the results yielded from SVD-based scheme [9]. The thresh value T equals 0.028 and the initial value of LM is 0.123 in order to make PSNR of the embedded image Lena 46.41 dB. And the thresh value T equals 0.040 and the initial value of LM is 0.123 in order to make PSNR of the embedded image Plane 42.97 dB. For image Baboon, the thresh value T and the initial value of LM are 0.042 and 0.2, respectively. And PSNR of Baboon is 40.15 dB. Simulation of some image processing attacks on three images has been performed to validate the proposed watermark scheme. They are JPEG compression with quality factor 70, noise pollution, cropping, sharpening and blurring. PSNR values for each attacked image are: Lena (38.352 6, 20.816 9, 10.576 4, 34.254 7, 40.744 9 dB), Plane (37.342 1, 20.489 4, 9.1 142, 31.958 6, 38.657 3 dB), and Baboon (32.260 0, 13.537 3, 10.086 3, 24.682 4, 30.856 7 dB).
The comparison results between this scheme and Sun’s method [11] is shown in Table 3. Sun’s scheme does not work well on noise pollution, and the BER values are higher than 0.45 for each embedded image. But, the watermark can be correctly identified by our method, and the BER is less than 0.1. This can illustrate that the robustness of our method on noise pollution is better than the SVD-based scheme. For cropping attack, PCC makes the embedded (or extracted) blocks cover whole image, so BER of our scheme is less than 0.1, which is higher than Sun’s scheme. The robustness to resist sharpening and blurring is strong and the BER values of these two attacks are less than 0.1. BER of image Lena to resist sharpening attack is only 0.005 9. All of these show that the extracted watermark image is clear enough to be an authentication or annotation.
Table 3 Comparison of our scheme and Sun et al’s scheme [11]

However, our approach does not work well on JPEG compression, and the average BER is higher than that of Sun’s scheme. Because in Sun’s scheme, the largest coefficient, D(1, 1), is extracted from each D component and quantized by using a predefined quantization coefficient, and the largest coefficient can resist JPEG compression better. Therefore, these comparison results in Table 2 and Table 3 indicate that our scheme has stronger robustness in most signals attacks except JPEG compression.
4.3 Security analysis
Kirchhoff’s criterion is often used to assess the usability of cryptograph methods and systems: All algorithms must be public, and only the keys are secret. The security of our algorithm only relies on the initial value of LM, which meets Kirchhoff’s criterion. We define the similarity to evaluate the security of this algorithm. In Fig.6, 2 500 keys are selected to generate PCC, and it can be seen that the similarity between PCCs generated by the same key are 1, otherwise, nearly zero.
![]() (12)
(12)
 (13)
(13)
where Eq.(12) is a symbol function. O(i) and O(j), T(i) and T(j) express the original coordinates, the corresponding coordinates in PCC, respectively. p and q are the sizes of two-dimensional PCC.

Fig.6 PCC similarity test result
Fig.7 shows the original watermark image and three extracted watermark images from Lena, Baboon, and Plane by using wrong key. The BERs of three watermark images are 0.493 2, 0.503 9 and 0.5, respectively, and the normalized correlation values are 0.013 7, -0.007 8 and 0, respectively. We can see that the extracted watermark images with wrong key are not clear. These prove that the security of our scheme is high enough not only from the visual quality intuitively, but also form the test criterion (BER and NC). All of these indicate that chaotic system enhances the security of the algorithm. Assume that there are N blocks, and r blocks are selected to

Fig.7 Original watermark image (a) and extracted watermark images with wrong keys from Lena (b), Baboon (c) and Plane (d)
embed the watermark. 0-bit numbers and 1-bit numbers are r0 and r1, respectively. The probability of getting correctly decoded bits is
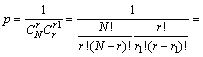
 (14)
(14)
Assume that 32×32 blocks are selected from (512÷ 4)×(512÷4) blocks, and the 0-bit number is the same as 1-bit number. The probability of getting correctly decoded bits is near to zero. Therefore, the security of this scheme is so high that it can resist the exhaustive attack method effectively.
5 Conclusions
1) After synthesizing the good characteristics of chaotic system and QR factorization, a novel robust digital image watermarking algorithm is put forward.
2) Because of the invariant characteristic in Q column of QR factorization, watermarks can be embedded without introducing obviously the alternation to the host images, and the robustness of this scheme is improved.
3) Pseudorandom circular chain (PCC) generated by logistic mapping (LM) is used to select the embedding blocks. So, the security of this scheme is very high, and the key space is big enough.
4) Performance comparisons with the existing schemes further demonstrate the effectiveness of the proposed scheme. In the future, we will extend our scheme to transform domain such as the discrete wavelet transform (DWT) to provide higher robustness to resist JPEG compression with lower distortion.
References
[1] HO A T S, ZHU X Z, SHEN J, MARZILIANO P. Fragile watermarking based on encoding of the zeroes of the z-transform [J]. IEEE Trans on Information Forensics and Security, 2008, 3(3): 567-569.
[2] PHAN R C W. Tampering with a watermarking-based image authentication scheme [J]. Pattern Recognition, 2008, 41(11): 3493-3496.
[3] NI Rong-rong, RUAN Qiu-qi, ZHAO Yao. Pinpoint authentication watermarking based on a chaotic system [J]. Forensic Science International, 2008, 179(1): 5 4-62.
[4] SONG Wei, HOU Jian-jun, LI Zhao-hong. SVD and pseudorandom circular chain based watermarking for image authentication [J]. Journal of Beijing Jiaotong University, 2008, 32(2): 71-75. (in Chinese)
[5] ALTUN O, SHARMA G, CELIK M U, BOCKO F M. A set theoretic framework for watermarking and its application to semi-fragile tamper detection[J]. IEEE Trans on Information Forensics & Security, 2006, 1(4): 479-492.
[6] MAHDIAN B, SAIC S. Blind authentication using periodic properties of interpolation [J]. IEEE Trans on Information Forensics & Security, 2008, 3(3): 529-538.
[7] SANG Jun, MOHAMMAD S A. Fragility and robustness of binary-phase-only-filter-based fragile/semi-fragile digital image watermarking [J]. IEEE Trans on Instrument & Measurement, 2008, 57(3): 595-606.
[8] ZHANG Hong-bin, YANG Chen. Image authentication scheme based on JPEG invariant and semi-fragile watermarking [J]. Journal of Beijing University of Technology, 2004, 30(2): 214-218. (in Chinese)
[9] SUN Rui, SUN Hong, YAO Tian-ren. A SVD and quantization based semi-fragile watermarking technique for image authentication [C]// Proc IEEE ICSP2002, 6th Internal Conference on Signal Processing. Beijing: IEEE, 2002: 1952-1955.
[10] ZHU Cong-xu, CHEN Zhi-gang. A novel spatial domain digital watermarking algorithm based on chaotic map [J]. Journal of Central South University of Technology: Science and Technology, 2005, 36(2): 272-276. (in Chinese)
[11] CHANG Chin-chen, TSAI Piyu, LIN Chia-chen. SVD-based digital image watermarking scheme [J]. Pattern Recognition Letters, 2005, 26(6): 1577-1586.
[12] TSUI T K, ZHANG Xiao-ping, ANDROUTSOS D. Color image watermarking using multidimensional Fourier transforms [J]. IEEE Trans on Information Forensics & Security, 2008, 3(1): 16-26.
[13] BRIASSOULI A, STRINTZIS M G. Locally optimum nonlinearities for DCT watermark detection [J]. IEEE Trans on Image Processing, 2004, 13(12): 1604-1617.
[14] BYUN K, LEE S, KIM H A. A watermarking method using quantization and statistical characteristics of wavelet transform [C]// Proc IEEE PDCAT2005, Sixth International Conference on Parallel and Distributed Computing, Applications and Technologies. Dalian: IEEE, 2006: 689-693.
[15] LI En-ping, LIANG Hua-qing. Blind image watermarking scheme based on wavelet tree quantization robust to geometric attacks [C]// Proc IEEE WCICA2006, Sixth World Congress on Intelligent Control and Automation. Dalian: IEEE, 2006: 10256-10260.
[16] LIN Wei-hung, HORONG Shi-jinn, KAO Tzong-wann, FAN Ping-zhi, LEE Cheng-ling, PAN Yi. An efficient watermarking method based on significant difference of wavelet coefficient quantization [J]. IEEE Trans on Multimedia, 2008, 10(5): 746-757.
[17] KANG Xian-gui. HUANG Ji-wu. ZENG Wen-jun. Improving robustness of quantization-based image watermarking via adaptive recover [J]. IEEE Trans on Multimedia, 2008, 10(6): 953-959.
[18] ZHU Cong-xu, CHEN Zhi-gang. A security multipurpose image watermarking system model and algorithm [J]. Journal of Image and Graphics, 2008, 13(5): 894-899. (in Chinese)
[19] AHN C J. Parallel detection algorithm using multiple QR decompositions with permuted channel matrix for SDM/OFDM [J]. IEEE Trans on Vehicular Technology, 2008, 57(4): 2578-2582.
Foundation item: Project(2007AA01Z241-2) supported by the National High-tech Research and Development Program of China; Project(2006XM002) supported by Beijing Jiaotong University Science Foundation, China; Project(0910KYZY55) supported by the Fundamental Research Funds for the Central University in China
Received date: 2009-05-19; Accepted date: 2010-05-28
Corresponding author: SONG Wei, PhD; Tel: +86-10-51688396; E-mail: recluse.sw@gmail.com

