铜精炼过程中液化气流量实测数据有效性检测方法

鄂加强，李娟，邓元望，彭雨，李光明，贾国海

(湖南大学 机械与运载工程学院，湖南 长沙，410082)

摘  要：针对铜精炼过程中液化气流量测量系统各传感器本身不精确、易受环境噪声以及人为干扰等因素的影响等问题，利用模糊综合评判理论和自动获取权重的混沌优化神经网络方法，通过对隶属函数的选择和综合评判权重的自适应调整，识别突变引起的误差以及连续长时间出现的误差并剔除变化较小的误差，从而提出一种铜精炼过程中液化气流量实测数据有效性检测方法。研究结果表明：在铜精炼过程中，经有效性检验的液化气标准板孔流量测量模型的质量流量最大相对误差小于2.75%，与不经有效性检验的质量流量最小相对误差相比至少低2.0%，有效地解决了实际复杂环境中多传感器实时数据采集的野值所导致的实测结果精度降低问题。

关键词：神经网络；混沌优化算法；模糊；有效性

中图分类号：TF811          文献标志码：A         文章编号：1672-7207(2010)04-1410-08

A validity test method of measurement data about liquefied petroleum gas flux in copper refining process

E Jia-qiang, LI Juan, DENG Yuan-wang, PENG Yu, LI Guang-ming, JIA Guo-hai

(College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China)

Abstract: Based on the effects such as the imprecision of sensors, environmental noise and human-caused disturbance in measurement system about liquefied petroleum gas flux in copper refining process, a validity test method of measurement data about liquefied petroleum gas flux in copper refining process was presented by using fuzzy comprehensive evaluation and chaotic optimization neural network algorithm with the ability of getting weight automatically, the errors from signal jump and the longtime errors were recognized and the errors of small rate were eliminated using subject function selection and adaptive adjustment of comprehensive evaluation. The results show that maximum relative error can be less than 2.75% and the relative error is less than 2.0% compared with that not being tested, which can solve the problems of low precision caused by the outliers from multi-sensor information fusion data in complicated environment.

Key words: neural network; chaotic optimization algorithm; fuzzy; validity

                                      

铜火法精炼系统是一个非常复杂的高温、多   相、非线性作用机制的宏观复杂系统^[1-2]，具有多变量、非线性、强耦合、大滞后等特点，其液化气流量参数检测精度直接影响整个铜精炼炉的生产效率、产品质量以及与操作安全^[3-4]。但在包含温度传感器、湿度传感器、压力传感器以及差压传感器的液化气流量参数实际测试系统中，不能保证来自每个传感器的测量值都是正确的。在通常情况下，由于传感器本身不精确以及环境噪声和受人为干扰等因素的影响，往往会使实测数据具有一定程度的不确定性^[5-6]，主要表现在信息本身不完全、获得信息不可靠、表达信息不成熟以及各种信息之间互相矛盾等，这将导致某个传感器在某次测量中可能产生虚假甚至错误的测量数据，这样的测量数据被称为野值。若将这些野值信息送入实际液化气测试系统，将会降低液化气实际测试结果的精度。因此，在进行液化气流量参数测量以前，必须先对来自所有传感器的测量值进行判断、识别等。传统的多传感器融合数据有效性检测方法主要有残差x²检验法^[7]和数据变化率检验法^[8]。这2种数据有效性检测方法对于由突变引起的粗大误差有较好的检测和隔离功能，但存在较大的缺陷，容易导致软故障发生，如：残差x²检验法对于由惯性元件等非直接作用于滤波量测值的状态变量引起的故障不是很敏感，虽然系统状态产生很大的估计误差，但残差一直很小，因而造成漏检^[9-10]；数据变化率检验法是利用检测时间点之前的N个数据的变化率来计算剔值带，若传感器软故障发生的时间超过了检测时间，则采用该方法就可能得出错误的判断。为此，本文作者利用模糊综合评判理论以及自动获取权重的混沌优化神经网络方法，提出一种多传感器信息融合数据有效性检测方法，对铜精炼过程中液化气流量实测数据有效性进行检测。这种方法通过对隶属函数的选择和模糊综合评判权重的自适应调整，有利于更准确地检测各个传感器输出数据的有效性。

1  铜精炼过程中液化气流量测量模型

1.1  铜精炼过程中液化气标准孔板流量测量模型

用标准孔板流量计对铜精炼过程中液化气质量流量进行测量时，铜精炼过程中液化气质量流量M与压差Δp和液化气密度ρ_f之间满足以下关系^[9-10]：

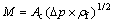            (1)

其中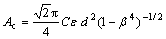：；β=d/D；D= D₂₀[1+λ(T_f -293)]；ε=1-(0.41+0.35β⁴)Δp/(p_f×k)；A_c为仪表系数；C为标准孔板流量计的流出系数，由Stolz方程^[10-11]给出；Δp为标准孔板流量计的压差；d为标准孔板的最小开孔截面直径；β为直径比；D为液化气管道内径；λ为液化气管道材料的线膨胀系数；T_f为铜精炼过程中液化气热力学温度；D₂₀为液化气管道在温度为20 ℃时的内径；ε为流束膨胀系数；k为铜精炼过程液化气的定熵指数。

由铜精炼过程中液化气质量流量计算式(1)可知：要想获得铜精炼过程中液化气的真实流量，必须确定液化气密度与差压。若铜精炼过程中液化气密度测量不准确，则即使进行高精度的差压测量，也不会使铜精炼过程中液化气质量流量与液化气体积流量的测量精度提高，反而会使液化气测量结果存在较大误   差。由于铜精炼过程中液化气为液化气和水蒸气组成的混合气体，一般是通过测量某一工况下的压力p₁和温度T₁来间接计算其密度，此外，还必须知道铜精炼过程中液化气中水蒸气的含量，即液化气的相对湿度。若将铜精炼过程中液化气中的水蒸气视为理想气体，则水蒸气的密度ρ_s和相对湿度满足以下关系：

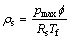               (2)

式中：p_max为温度T_f时铜精炼过程液化气中水蒸气所对应的最大分压力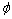；为铜精炼过程液化气的相对湿度；R_s为水蒸气的气体常数，R_s=461.9 J/(kg·K)。

由道尔顿分压定律可知：铜精炼过程液化气中干液化气所占的压力p_gf1为铜精炼过程液化气的总压力p_f减去水蒸气所占的分压力p_max之差，则铜精炼过程液化气中干液化气成分的密度满足：

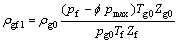        (3)

式中：ρ_g0为标准状态下铜精炼过程中干液化气的密度；T_g0为标准状态下的热力学温度；Z_f为工况下干液化气压缩系数；Z_g0为标准状况下干液化气压缩系数；p_g0为标准状态下干液化气压力。因此，铜精炼过程液化气的密度可表示为：

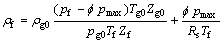     (4)

将式(4)代入式(1)，可以得出使用标准孔板流量计对铜精炼过程液化气流量的测量模型：

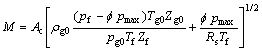  (5)

1.2  铜精炼过程中液化气流量测量系统

铜精炼过程中液化气流量测量系统如图1所示。采用标准节流件即标准孔板作为检测元件，包括温度传感器、湿度传感器、差压传感器、压力传感器。铜精炼过程中液化气流量测量所采集的数据不可避免地受到各种噪声的干扰，从而可能导致铜精炼过程中液化气流量测量信号发生波动和跳动，为此，必须对温度传感器、湿度传感器、差压传感器、压力传感器的测量值进行检测、识别及其剔除，从而在较大程度上提高铜精炼过程中液化气流量的测量精度。可见：对温度传感器、湿度传感器、差压传感器、压力传感器的实测数据进行有效性检测十分重要。

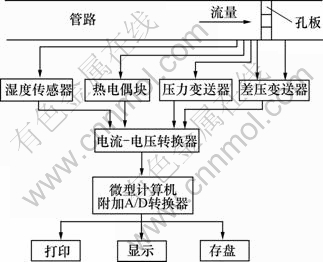
图1  铜精炼过程中液化气流量测量过程

Fig.1  Measurement processes of liquefied petroleum gas flux in copper refining process

2  基于神经网络的模糊综合评判检测法

2.1  模糊综合评判的基本原理

模糊综合评判又称模糊多元决策，它包括3个要素^[11]：(1) 因素集U={u_l, u₂, …, u_n}；(2) 评语等级集V={v_l, v₂, …, v_m}；(3) U到V的模糊关系矩阵R。

在综合评判时，还要考虑各个因素对评定等级所起的作用，即权重，记为A，它是因素论域上1个模糊子集，A={a_l, a₂, …, a_n}。

模糊综合评判的实现过程如下：(1) 建立隶属函数，确定隶属度；(2) 建立模糊关系R；(3) 确定权重A；(4) 选择模糊变换规则；(5) 由权重A和模糊关系矩阵R通过一定的模糊变换规则，即可实现模糊综合评判^[12]：

C=A·R                  (6)

即

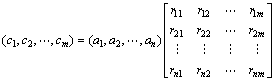
由此可见：综合评判结果集B主要取决于权重集A。因此，在模糊综合评判中，权重的确定是关键。

2.2  自动获取权重的混沌优化神经网络方法

权重是铜精炼过程液化气流量测量系统中各检测参数在有效性评判中的重要性程度，实质上是铜精炼过程液化气流量测量系统各检测参数与其测量数据有效性的相关程度，相关程度越高，则其权重就越大；相关程度越低，则其权重就越小。

铜精炼过程中液化气流量测量系统各检测参数与其测量数据有效性之间的关系极其复杂，它们具有不确定性、模糊性和高度非线性，仅凭经验人为地确定其权重，不但没有深入挖掘复杂关系内部的结构信息，有时甚至是错误的，同时，这些复杂关系不可能由精确的数学模型来描述。为此，将模糊理论与神经网络理论相结合，将神经网络的学习机制引入模糊系统，通过神经网络的学习功能获得各检测参数与铜精炼过程中液化气流量测量数据有效性间的网络权系数，进而转换成模糊综合评判所需的权重。

2.2.1  函数链神经网络

在图2所示的函数链神经网络中，w_j(j=1, 2, …, n)为网络的连接权值，其权值的个数与反非线性多项式的阶数相同，即j=n。

函数链神经网络的输入值为：u_l, u₂, …u_j, …, u_n。函数链神经网络的输出值y^est为：

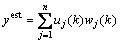           (7)

式中：w_j(k)为第k步时第j个连接权值。

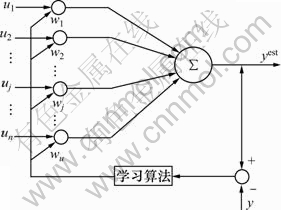
图2  函数链神经网络示意图

Fig.2  Sketch map of function chain neural network

在样本训练过程中，将函数链神经网络的输出估计值y^est与第k步测量输入值u_l, u₂, …, u_j, …, u_n对应的实际多传感器信息融合数据有效性y进行比较，经函数链神经网络学习，求出函数链神经网络的输出估计值与第k步测量输入值u_l, u₂, …, u_j, …, u_n对应的实际多传感器信息融合数据有效性y的均方差在全局范围内的最小值：

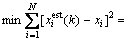
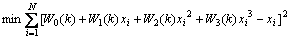
s.t.  c_j≤w_j≤d_j               (8)

即该最小值是关于权值w_j (j=1, 2, …, n)的函数。

2.2.2  自适应混沌

优化算法

在给定权值w_j的取值范围[0, 1]中，利用自适应变尺度混沌优化算法^[12]对式(8)所示的全局优化问题求解，即可得到满足均方差在全局范围内的最小值时的权值w_j (j=1, 2, …, n)。

选择折叠次数无限一维自映射：

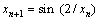, -1≤x_n≤1,  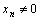    (9)

作为产生搜索迭代用的混沌变量的混沌模型，用K₁和K₂分别表示粗、细迭代次数，混沌优化算法的基本步骤如下。

Step 1：算法初始化。置K₁=1，K₂=1，并给定2个较大的正整数N₁和N₂，用随机数产生x₀，代入式(9)所示的混沌模型，产生i个混沌变量x_{i, n+1}(i=1, …, n)作为产生搜索迭代用的混沌变量。

Step 2：混沌变量在设计变量区间上进行粗略转化。利用式(10)将以上产生的第i个混沌变量由取值范围[-1, 1]变换到优化设计变量η与n的数值区间[c_i, d_i]上的混沌变量。

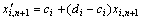          (10)

Step 3：用混沌变量进行粗迭代搜索。令x_i(K₁)=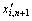，计算优化解 f_i(K₁)。令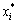= x_i(0)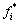，= f_i(0)，则：

(1)     若f_i(K₁)≤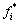，则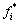= f_i(K₁)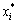，= x_i(K₁)。

(2) 若f_i(K₁)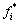＞，则放弃x_i(K₁)。当K₁≤N₁时，进入下一次迭代，K₁：=K₁+1；当K₁＞N₁时，结束粗迭代。

Step 4：混沌变量搜索区间缩小。

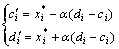             (11)

式中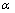：为收缩因子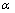，∈(0，0.5)。

为了保证新范围不至于越界，进行如下处理：若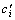＜c_i，则设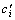=c_i；若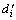＞d_i，则设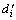=d_i。因此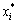，在新区间[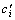,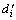]上进行还原处理后的量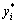由下式   确定：

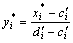                (12)

Step 5：混沌变量在设计变量区间上的细转化。如果经过Step 3的若干搜索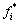，都保持不变，则利用式(12)把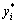与x_{i, n+1}的线性组合作为新的混沌变量，用此混沌变量进行搜索。

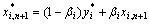         (13)

式中：β_i为自适应调节系数，0＜β_i＜1。

自适应调节系数β_i采用如下方法进行自适应   确定：

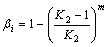             (14)

式中：m为整数，根据优化目标函数而定，本文取m=2。

在进行细迭代搜索初期，由于(x₁, x₂, …, x_n)变动较大，故要求β_i较大，随着搜索的进行，逐渐接近最优点，故要求β_i较小，以便在(x^*₁, x^*₂, …, x^*_n)所在的较小范围内进行搜索。

Step 6：用混沌变量进行细迭代搜索。令x_i(K₂)=  x^*_{i, n+1}，计算优化解 f_i(K₂)。

(1) 若f_i(K₂)≤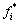，则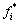= f_i(K₂)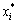，= x_i(K₂)；

(2) 若f_i(K₂)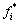＞，则放弃x_i(K₂)。当K₂≤N₂时，进入下一次迭代，K₂：=K₂+1；当K₂＞N₂时，结束细迭代。

当得到最优解w_j (j=1, 2, …, n)后，将其作为网络权系数保存起来。

2.2.3  网络权系数向模糊综合评判权重的转换

当函数链神经网络权系数被确定后，就可以实现从W向A的转换：

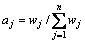               (15)

2.3  模糊关系矩阵确定

对铜精炼过程中液化气流量测量系统多传感器数据进行模糊处理，即对各个传感器的测量值进行量化。针对不同状态参数对信息融合精度的影响方式，可采用隶属函数和相关分析的方法对各个传感器的测量值进行模糊处理。

目前，确定隶属函数的各种方法均依靠经验，从实践效果中进行反馈，不断校正认识，以达到预定的目标。在很多情况下，用一些常见的分布函数作为隶属函数来近似表达一些模糊变量是最简便的方法。图3所示为进行模糊化计算可能性分布所用到的三角形隶属函数，由此可得某一传感器的某个测量值为有效的可能性分布计算公式为：

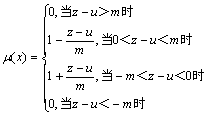      (16)

式中：z为系统的测量值；u为计算可能性分布的依 据，可以通过先验知识进行计算；m为模糊子集的边界值，用于确定测量值可能性分布的必要条件，可以根据实际应用情况进行自适应调整，一般取m=2σ；σ为相应测量值的方差。由式(16)可以得到铜精炼过程中液化气流量在实测过程中输入参数相对应的模糊关系矩阵，并对铜精炼过程液化气流量实测数据有效性进行检测。

图3  三角形隶属函数

Fig.3  Triangle subjection function

3  铜精炼过程中液化气流量实测数据有效性检测

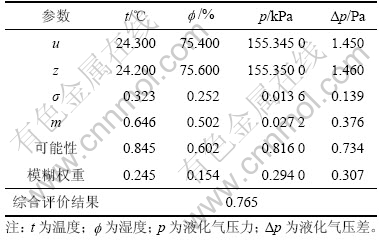
利用以上各传感器精确度较高的200组数据进行检测，并同时采用质量流量计测出铜精炼过程中200个液化气质量流量，作为函数链神经网络的训练样本。将训练好的函数链神经网络权系数经归一化，其模糊权重如表1所示。据此，可对铜精炼过程中液化气流量传感器数据进行有效性评判。

从表1可以看出：这组测量值是正确的。一旦系统出现野值信息，就应根据不同的情况及时地采取不同的措施，否则会使精度降低，难以保证铜精炼过程中液化气流量测量系统的正常工作。

3.1  铜精炼过程中液化气流量实测数据有效性检测  仿真

为了将基于神经网络的模糊综合评判检测法与残差x²检验法和数据变化率检验法进行对比，本文采用以上3种方法对铜精炼过程中液化气流量实测数据有效性进行仿真研究。

表1  铜精炼过程中液化气流量测量数据有效性检测

Table 1  Validity test of measurement data about liquefied petroleum gas flux in copper refining process

在液化气流量测量系统中，采样时间τ₀为0.5 s，共测得1 200组数据，测量数据均为正确值，融合后的温度、湿度、差压、压力曲线结果与时间τ之间关系如图4所示。将测量过程数据进行如下修改：

(1) 将数据文件中第95组的温度、湿度、压力以及压差4个测量值都置为0；(2) 将第190组温度置为27.5 ℃；(3) 将第380组至470组的温度、湿度、压力以及压差这4个测量值都置为0。

图5~7所示分别表示经过3种不同方法进行误差剔除后铜精炼过程中液化气流量测量系统各传感器参数变化曲线。从图5可以看到：残差x²检验法对于突变引起的误差可以识别，但不能剔除；当突变引起的误差较小时，采用该方法很难对其进行识别。从图6可以看出：在380~470连续步长时间内，采用数据变化率检验法出现误差。这说明当突变引起的误差很小时，数据变化率检验法无法对其识别。从图7可以看出：数据有效性神经网络模糊综合判别检测法明显克服了以上2种方法的缺点。

3.2  铜精炼过程中液化气流量实测数据有效性检测应用效果

铜精炼过程中液化气管道上同时安装科里奥利质量流量计、标准孔板流量计，对所测得质量流量进行对比实验。以科里奥利质量流量计的测量读数为基准，未经有效性检测的铜精炼过程中液化气标准孔板流量测量模型的质量流量测量误差与经神经网络模糊综合评判检测后的误差如图8所示。

由图8可以看出：液化气压力p在110~190 kPa之间，未经有效性检测的铜精炼过程液化气标准孔板流量测量模型质量流量最小相对误差大于4.75%，而经神经网络的模糊综合评判检测后最大相对误差小于2.75%，大大提高了测量精度。

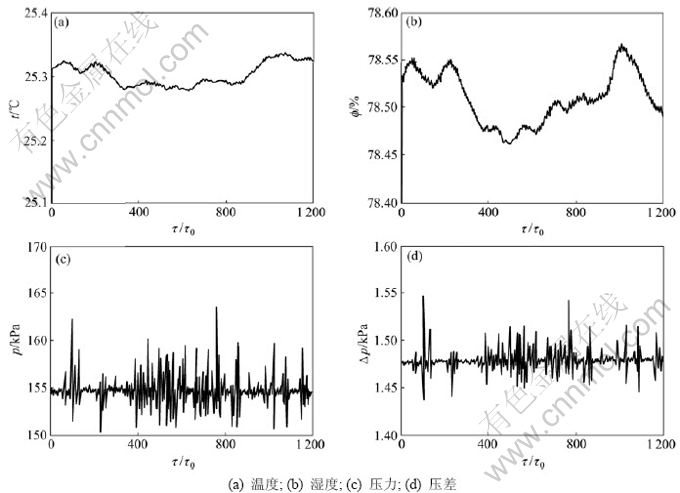
图4  铜精炼过程中液化气流量测量系统传感器参数曲线

Fig.4  Sensor parameters curves of measurement system about liquefied petroleum gas flux in copper refining process

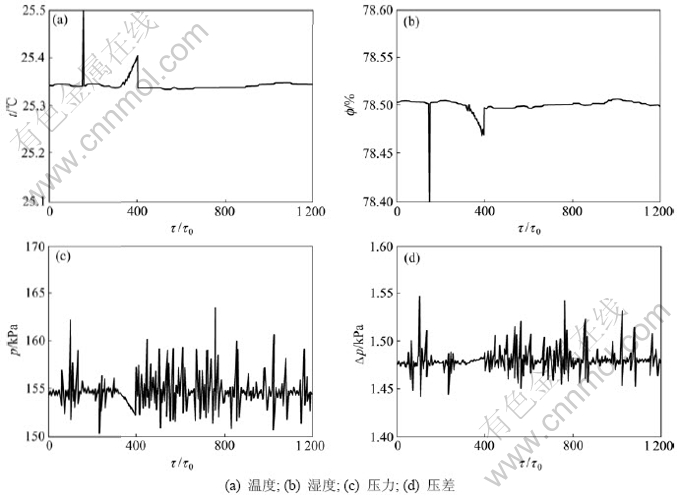
图5  残差x²检验后的传感器参数曲线

Fig.5  Sensors parameters curves after x² test

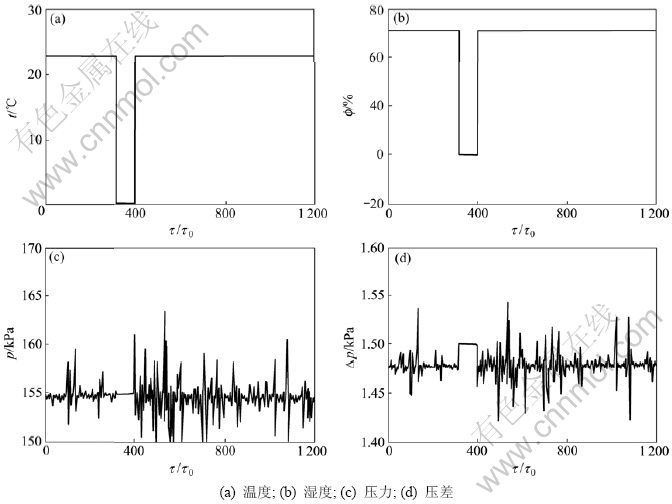
图6  数据变化率检验后传感器参数曲线

Fig.6  Sensor parameters curves after data rate test

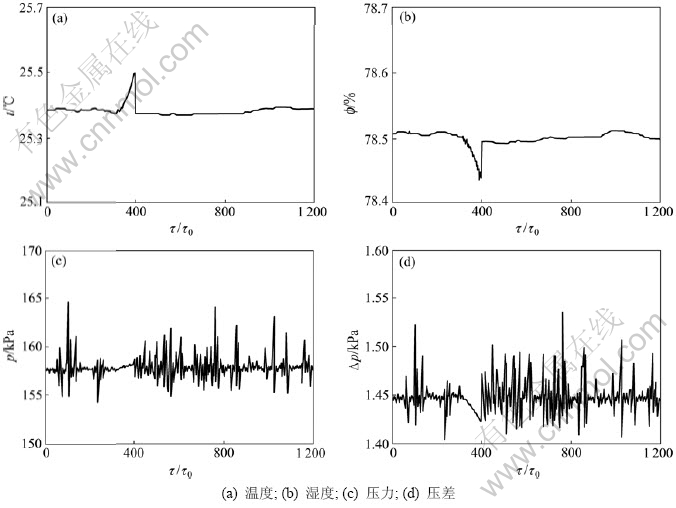
图7 神经网络的模糊综合评判检测后传感器参数曲线

Fig.7  Sensor parameter curves after fuzzy comprehensive evaluation based on artificial neural network

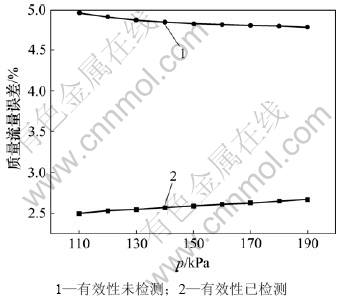
图8  铜精炼过程中液化气质量流量测量相对误差

Fig.8  Relative errors from liquefied petroleum gas flux in copper refining process

4  结论

(1) 针对传统的数据有效性判断方法存在缺陷的实际情况，提出了一种基于神经网络的信息融合数据有效性模糊综合评判方法，并对管道煤气流量计量系统多传感器信息融合数据进行了评判。结果表明：基于神经网络的信息融合数据有效性模糊综合评判方法能够识别突变引起的误差以及连续长时间出现的误差，同时也能剔除变化较小的误差。

(2) 在铜精炼过程中，液化气标准孔板流量测量模型经神经网络的模糊综合评判检测后，其质量流量最大相对误差小于2.75%，与不对其有效性进行检测的相对误差相比至少低2.0%，具有较高的精度。

参考文献：

[1] Moskalyk R R, Alfantazi A M. Review of copper pyrometallurgical practice: today and tomorrow[J]. Minerals Engineering, 2003, 16(10): 893-919.

[2] 鄂加强. 铜精炼过程优化建模与智能控制[M]. 长沙：湖南大学出版社, 2006: 59-70.
E Jia-qiang. Optimal modeling and intelligent control about copper refining process[M]. Changsha: Hunan University Press, 2006: 59-70.

[3] HU Yan-yu, GUI Wei-hua, LI Yong-gang. Flux-measuring approach of high temperature metal liquid based on BP neural networks[J]. Journal of Central South University of Technology, 2003, 10(3): 244-247.

[4] Georgalli G A, Eksteen J J, Reuter M A. An integrated thermochemical-systems approach to the prediction of matte composition dynamics in an Ausmelt nickel–copper matte converter[J]. Minerals Engineering, 2002, 15(11): 909-917.

[5] 管桦, 魏瑞轩. 一种用于传感器故障检测的改进残差检验法[J]. 空军工程大学学报: 自然科学版, 2005, 6(3): 26-28.
GUAN Hua, WEI Rui-xuan. A modified residual test method applied to sensor failure detection[J]. Journal of Air Force Engineering University: Natural Science Edition, 2005, 6(3): 26-28.

[6] 王志胜, 王道波, 蔡宗琰. 用于缓变故障检测的残差检验法[J]. 西安电子科技大学学报, 2004, 31(3): 479-482.
WANG Zhi-sheng, WANG Dao-bo, CAI Zong-yan. An improved residual test method for soft fault detection[J]. Journal of Xidian University, 2004, 31(3): 479-482.

[7] Ren D. Failure detection of dynamic systems with the state chi-square test[J]. Journal of Guidance, Control and Dynamics, 1994, 17(2): 271-277.

[8] 朱容生, 施小成. 一种用于GPS数据处理中剔除野值的算法[J]. 中国惯性技术学报, 2000, 8(2): 27-30.
ZHU Rong-sheng, SHI Xiao-cheng. An outliers eliminating algorithm for GPS data processing[J]. Journal of Chinese Inertial Technology, 2000, 8(2): 27-30.

[9] 鄂加强, 时章明, 刘春洋. 基于蒸汽压方程下的管道煤气在线计量系统[J]. 计量学报, 2004, 25(1): 35-37.
E Jia-qiang, SHI Zhang-ming, LIU Chun-yang. On-line measurement system for gas flux in the pipeline based on vapour pressure equation[J]. Acta Metrologica Sinica, 2004, 25(1): 35-37.

[10] 鄂加强, 张华美, 王耀南, 等. 基于函数链神经网络的管道煤气流量计量系统[J]. 中南大学学报: 自然科学版, 2006, 37(5): 976-980.
E Jia-qiang, ZHANG Hua-mei, WANG Yao-nan, et al. Measurement system for gas flux in pipeline based on function chain neural network[J]. Journal of Central South University: Science and Technology, 2006, 37(5): 976-980.

[11] 鄂加强. 智能故障诊断及其应用[M]. 长沙: 湖南大学出版社, 2006: 98-156.
E Jia-qiang. Intelligent fault diagnosis and its application[M]. Changsha: Hunan University Press, 2006: 98-156.

[12] E Jia-qiang, WANG Chun-hua, WANG Yao-nan, et al. A new adaptive mutative scale chaos optimization algorithm and its application[J]. Journal of Control Theory and Applications, 2008, 6(2): 141-145.

                                              

收稿日期：2009-07-10；修回日期：2009-09-20

基金项目：湖南省自然科学基金资助项目(06JJ50103)

通信作者：鄂加强(1972-)，男，湖南湘潭人，博士，副教授，硕士生导师，从事智能信息融合处理、智能检测与智能故障诊断研究；电话：13187041842；E-mail: ejaqiang@126.com

(编辑 陈灿华)