J. Cent. South Univ. Technol. (2008) 15(s1): 438-442
DOI: 10.1007/s11771-008-395-y
Rock bending creep and disturbance effects
FU Zhi-liang(付志亮)1, 2, ZHENG Ying-ren(郑颖人)2, LIU Yuan-xue(刘元雪)2
(1. Key Laboratory of Ministry of Education Co-sponsored by Province and Ministry Laboratory of
Safety and High Efficient Coal Mining, College of Energy Resources and Safety Engineering,
Anhui University of Science and Technology, Huainan 232001, China;
2. Department of Architectural Engineering, Logistical Engineering University, Chongqing 400041, China)
Abstract: The bending creep and its disturbance effects of red sandstone rock beam and oil shale rock beam were studied by adopting the self-developed gravitation level style rock creep test machine and bending creep test system, and the constitutive equations were established. It is found that fracture morphology of rock beams under no disturbance load is regular, cracking position of fractures is on part of loading concentration, the crack starts from a neutral plane. However, fracture morphology of rock beams under disturbance load is irregular, cracking position of fractures deviates from a neutral plane. Delayed instability of rock beam occurs for some time under constant disturbance load. When disturbance load is beyond a certain range, suddenly instability of occurs rock beam in a certain time. The results show that there is a guiding significance for creep stability in the geotechnical engineering fields.
Key words: rock beam; bending creep; disturbance load; gravity; delayed instability
1 Introduction
During the mining ore body and underground structure excavation, layered rock mass suffers from blasting, excavation, shaft station passing, mining disturbance and other disturbance. Especially during deep mining，it is found that the stability of high stress rock mass is more obviously influenced by the external disturbance with increasing original static stress. When the roadways surrounding rock is endured by very high static stress，even a small dynamic disturbance may lead to its plastic destroying and result in a domino effect in the deep mining. Roadways experience low static stress and high static stress from the view point of damage mechanics[1-5]. The results show that rock laneway is in the different states of stability when rock is at different depths of ground, and roadways are stable when they are at the low depth of ground; roadways are close to or in the critical state of stability when roadways are at larger depth of ground, and the less disturbance may cause fractures to extend instantaneously and cosmically, leading to the roadways in stability, in the mean time, with much strain energy releasing fast; the occurrence of losing stability is easier in deep roadways that are on the condition of high ground stress than that in shallow roadways[6-11].
Main study subjects of rock beam bending focused on marble and red sandstone in the past. The research on soft rock hasn’t been conducted yet. Bending test is simple and practicable. In addition, this method can be conveniently applied to disturbance loads.
The aim of this paper is to investigate the mechanics properties of disturbance creep preliminarily by adopting longitudinal compression model of rock beam and combining with creep behavior of deep rock. It is very helpful for studying rock strata deformation and damage.
2 Test and method
Rock samples were collected from Longkou Mining Area of Shandong Province in China. The experiment included four kinds of rock beams, red sandstone and oil shale, which were divided into 12 groups altogether. There were 6 beams in every group, among which three rock beams of every group were used to measure damage loads in order to reduce discreteness of mechanics properties of samples and ensure the reliability of the test results. All of rock beams came from rock plate are cut by same stratigraphic horizon. The dimensions of the samples was 30.0 cm×3.0 cm×1.5 cm and 50.0 cm× 5.0 cm×2.5 cm. Test was conducted on bending creep disturbance instrument. Horizontality and span of steel rigid frame were adjusted, and then rock beam was put in good place. One end was fixed on cylindrical supporting, the other was rolling cylindrical supporting. The con-straints of rock beam can be considered simply supported beam (see Figs.1 and 2 ).
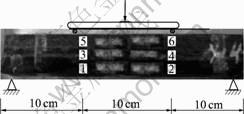
Fig.1 Sketch map of bending test of oil shale beam
In order to reduce sliding friction force caused by beam horizontal movement during lateral loading, steel roller shaft (its diameter was 5 mm) was put on the bottom of beam, rolling friction was replaced with sliding friction. The friction force was greatly reduced, reliability of data was further improved.
Loading mode was four-point bending, namely, pure bending, its dimensions were 10 cm×20 cm (see Fig.1).
Data were collected by resistance strain gauge (see Fig.2). Because the ratio of span to height of rock beam is 3/26, satisfying the condition of slender beams, so the plane hypothesis is applicable. Resistance strain gauge symmetrically is stuck on two sides and upper-down of rock beam pure bending. Six or ten strain gauges are suck on every beam, as shown in Fig.1.
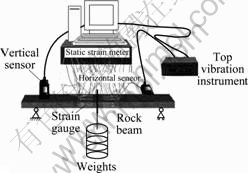
Fig.2 Sketch map of auto monitoring system of bending test
Weights were suspended above rock beam, which dropped like a free falling body, which had great impact on rock beam. Weights’ masses were 50, 100, 150, 200 and 250 g, respectively. Loading impulsive was produced by dropping different mass weights, impacting velocity was 4.75-4.87 m/s, and dropping height was 10-50 cm. Impacting repetitively on rock beam at the same height until rock beam destroy (see Fig.3).
3 Constitutive relations between two kinds of rocks
Before impacting, creep is slow. After impacting, formation occurs mainly at middle rock beam, and
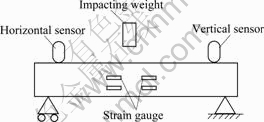
Fig.3 Sketch map of bending creep disturbance of rock beam
Fig.4 Fracture morphologies of rock beam and failure forms: (a) Red sandstone; (b) Oil shale
deformation is larger at the beginning, but deformation becomes stable after 0.1 ms. Horizontal and vertical creeps of samples are changed obviously under gravity impacting loads, and horizontal creep is less than vertical creep.
According to Fig.4, rock beam creep is divided into three stages. The first stage is oscillating stage when dropping hammer contacts instantaneously, impacting force comes to peak value quickly, and then attenuates fast. Creep increases instantly, which does not reach peak value. The second stage is stable stage. After going through the initial oscillating stage, rock impacting force is stabilized at a certain value and forms platform. The third stage is attenuating stage, after going through the stable stage, impacting force attenuates quickly until it decreases to zero. Because of vertical load applied on rock beam, vertical creep is produced.
From Fig.5, we find that fracture morphologies of rock beams without impacting loads is regular, cracking position of fractures is in the area of loading concentration, the crack starts from a neutral plane. Fracture morphology of rock beams under impacting disturbance loads is irregular, cracking position of frac-tures deviates from a neutral plane.
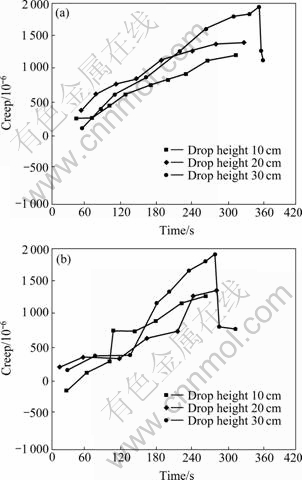
Fig.5 Curves of vertical creep and disturbance load of rock beam: (a) Red sandstone; (b) Oil shale
Seen from Fig.5, we can find that axial creep curves are of the characteristic of impacting fluctuation, wave peaks of axial creep curves go up quickly, and attenuate exponentially after reaching peak value.
Lateral micro-strains are maximum, they are 480 and 430 respectively, rise time are 230 s and 340 s, impacting time are 93 ms and 93 ms. After stabilizing for 47 ms, strain curve goes down slightly about 350 ms, and then rises to 950, rise time is 88 ms, impacting time is 24 ms. And then strain curve goes down slightly for 294 ms, the slope of curve is 60?, strain comes to 2 600, going- up time is 235 ms, and impacting time is 73 ms. The maximum axial micro-strain is -337, rise time is 50 ms impacting time is 120 ms; curve transition is 250 ms, micro-strain is -670, rise time is 40 ms, and impacting time is 76 ms.
The beam plate is supposed to longitudinal compression model. The model of time-dependent mechanical behavior of deep rock for plate beam under longitudinal compression is adopted. The mechanisms of roadway floor heave and delay rockbursting are preliminarily discussed. Time bifurcation for plate beam stability is analyzed. One end is fixed beam, the other is rolling supporting. Rock beam is simplified as model.
According to the symmetry of beam, choose half of beam to study. The coordinate system is established. Based on plane hypothesis, the section o-x of rock beam’s equilibrium equation is
M″(x, t)-pv″-q1(x, t)=q(x) (1)
where M(x, t) is bending moment at certain time, at time t and point x of rock beam; longitudinal load p is constant; v(w, t), is deflection at time t and point x; q1(x, t) is supporting force, and can be written as q1(x, t)= γ1(t)*, here γ1(t)* is relaxation function of rock beam with viscoelastic supporting; q(x) is supporting force of empty surface, it is zero without supporting. Arbitrary point’s strain on the cross section of rock beam is
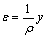(2)
which gives
or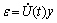 
where ρ is curvature radius;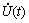 
is curvature. When v″≤0, then creep rate are obtained at time t
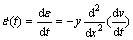(3)
Rock beam constitutive equation is
σ(t)=γ(t)*dε (4)
where γ(t)* is relaxation function of plane strain material; “*” is symbol for stieltjes convolution sign. Bending moment is written as[21-23]
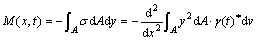
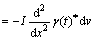(5)
Substituting q(x, t) and Eqn.(5) into Eqn.(1) yields
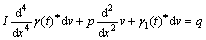(6)
where Eqn.(6) is creep damage equation of rock beam under plane strain condition. Here, disturbance state is considered only. When q1(x, t), q(x)≠0, Eqn.(6) can be simplified into
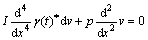(7)
Eqn.(7) is arranged by Laplace transform
(8)
Eqn.(8) is written as characteristic equation
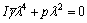(9)
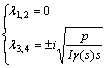(10)
When λ1, 2=0, rock beam has no deformation in image space, original space has no deformation, it is no
significant. For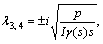 
rock beam has defor-
mation in image space. The deflection value of rock beam under disturbance load can be obtained by resolving the equation
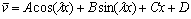(11)
where A, B, C and D are integral constants. They can be determined by boundary conditions. For fixed-end constraint, boundary conditions of image space are written as
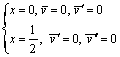(12)
Disturbance loads of rock beam in image space are
(13)
Then, for given disturbance load qd in image space, disturbance deformation time sd can be determined
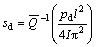(14)
where 
is inverse function, then 
Eqn.(12) is transformed by Laplace inverse transforms, creep damage load is obtained.
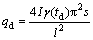(15)
Disturbance creep damage time is obtained
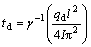(16)
where Eqns.(6)-(14) are similar to elastic form, but they are different in nature. Elastic compression yield load is concrete value, which has no relation with time. For viscoelastic creep, rock beam occurs delaying instability at some time under disturbance load qd, the three concrete conditions are discussed as follows.
1) Compression yield does not occur for quite a long time. Only rheology occurs, and its longitudinal loads were written as qd(+∞) (long term load).
2) When instantaneous instability occurs in a short time, longitudinal loads were written as qd(0) (instantaneous elastic critical load).
3) When load is qd(+∞)＜qd(t1)＜qd(0), delaying instability rock beam will occur in a finite time.
Seen from Fig.6, the model creep curve and test creep curve are fitted perfectly by linear fitting.
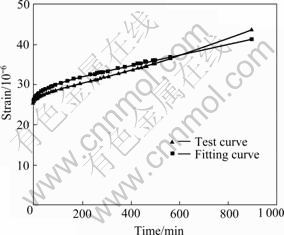
Fig.6 Fitting curve of rock creep
4 Conclusions
1) The bending creep deformational behavior and effects of disturbance on creep of the Laizhou red sandstone and a typical weak oil shale found in Longkou are presented and analyzed based on a series of multistage bending creep tests.
2) Fracture morphology of rock beams under no impacting loads is regular, cracking position of fractures is on the part of loading concentration, and the crack starts from a neutral plane. Fracture morphology of rock beams under impacting disturbance loads is irregular, cracking position of fractures deviates from a neutral plane.
3) Rock beam occurs delaying instability for some time under disturbance load. When load is beyond the range of qd(+∞)＜qd(t1)＜qd(0), rock beam will become
unstable at 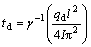time.
Acknowledgements
This research is financially supported by the National Natural Science Foundation (50174035 and 50474029). The experimental work was conducted at Key Laboratory of Ministry of Education Co-sponsored by Province and Ministry Laboratory of Mine Disaster Prevention and Control in Shandong University of Science and Technology (SDUST), Anhui University of Science and Technology.
References
[1] EXADAKTYLOS G E, VARDOULAKIS I, KOURKOULIS S K. Influence of nonlinearity and double elasticity on flexure of rock beams (I) [J]. Technical Theory, 2001, 38(22): 4091-4117.
[2] SINGH J G, UPADHYAY P C. Creep bending of rock beams [J]. International Journal of Rock Mechanics and Mining Science & Geomechanics, 1987, 5(2): 163-169.
[3] JIN Feng-nian, PU Kui-ying. Simulation of crack extension in three-point bending creep test [J]. Chinese Journal of Rock Mechanics and Engineering. 1997, 16(1): 51-58. (in Chinese)
[4] LI Xi-bing, LI Di-yuan, GUO Lei, YE Zhou-yuan. Study on the mechanical response of highly-stressed pillars in deep mining under dynamic disturbance [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(5): 922-928. (in Chinese)
[5] JIN Feng-nian. Comparison of tensile and compressive behaviours of rock [J]. Chinese Journal of Geotechnical Engineering, 1998(2): 31-33. (in Chinese)
[6] MAO Hai-jun, YANG Chun-he, LIU Jiang, et al. Testing study and modeling of creep behavior of slates [J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(6): 1204-1209. (in Chinese)
[7] ZUO Yu-jun, LI Xi-bing, MA Chun-de, et al. Catastrophic model and testing study on failure of static loadingrock system under dynamic loading [J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(5): 741-746. (in Chinese)
[8] FU Zhi-liang. Theoretical and experimental study on effects of disturbance to rock creep and damage characteristics [D]. Qingdao: Shandong University of Science and Technology, 2007. (in Chinese)
[9] FAN Qing-zhong. Experimental study on creep and its disturbance effect of rocks [D]. Qingdao: Shandong University of Science and Technology, 2006. (in Chinese)
[10] ZHANG Xiao-chun, HU Guang-wei, YANG Ting-qing. A stability analysis for time-dependence of plate-beam structure of rock [J]. Journal of Wuhan Transportation University, 1999, 23(2): 158-160. (in Chinese)
[11] HE Feng, WANG Lai-gui, YU Yong-jiang. Rock beam model of hang arch in operation goaf and rheological analysis [J]. Ground Pressure and Strata Control, 2005(4): 84-86. (in Chinese)
(Edited by CHEN Wei-ping)
Foundation item: Projects(50474029, 50174035) supported by the National Natural Science Foundation of China
Received date: 2008-06-25; Accepted date: 2008-08-05
Corresponding author: FU Zhi-liang, PhD, Associated professor; Tel: +86-554-6634368; E-mail: fuzhiliang2007@yahoo.com.cn
