J. Cent. South Univ. Technol. (2011) 18: 650-657

DOI: 10.1007/s11771-011-0743-1

Optimal control of cobalt crust seabed mining parameters based on simulated annealing genetic algorithm

XIA Yi-min(夏毅敏)¹, ZHANG Gang-qiang(张刚强)¹, NIE Si-jun(聂四军)²,

BU Ying-yong(卜英勇)¹, ZHANG Zhen-hua(张振华)¹

1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;

2. Guangxi Liugong Machinery Co. Ltd, Liuzhou 545007, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: Under the condition of the designated collection ratio and the interfused ratio of mullock, to ensure the least energy consumption, the parameters of collecting head (the feed speed, the axes height of collecting head, and the rotate speed) are chosen as the optimized parameters. According to the force on the cutting pick, the collecting size of the cobalt crust and bedrock and the optimized energy consumption of the collecting head, the optimized design model of collecting head is built. Taking two hundred groups seabed microtopography for grand in the range of depth displacement from 4.5 to 5.5 cm, then making use of the improved simulated annealing genetic algorithm (SAGA), the corresponding optimized result can be obtained. At the same time, in order to speed up the controlling of collecting head, the optimization results are analyzed using the regression analysis method, and the conclusion of the second parameter of the seabed microtopography is drawn.

Key words: cobalt crust; mining parameter; specific energy consumption; simulated annealing genetic algorithm

1 Introduction

Because of the great economic value and strategic significance of cobalt-rich crust, the world is witnessing a fierce enclosure competition in ocean mineral resources with cobalt-rich crust as the focus [1-2]. At present, the energy consumption is a prominent problem in the process of the collection of cobalt crust, so it should be reduced as much as possible [3]. The consumption is related to the structure parameters and working parameters of the collecting head. When the manufacture of the mineral collecting machine is completed, the structure parameters of the collecting head cannot be adjusted, but its working parameters can be adjusted according to the features of the microrelief of the seabed. The working parameters of the collecting head, such as feed speed, rotate speed and cutting depth, have an enormous influence on the crushing behavior [4]. Thus, it is necessary to establish an optimization model with the optimum working parameters. Applicable design methods are employed in such kind of model, and a group of suitable mining parameters are determined according to specific microtopography. For the optimization problems of multi-parameters and multi-extremum and nonlinear systems, it is not easy to get solutions with the traditional optimization method, or the partially optimal solutions can be obtained. Therefore, extracting objective mathematical model from the practical consideration must be resolved in the problem optimization design [5]. Currently, many scholars have combined genetic algorithm (GA) with simulated annealing (SA), and have optimized the design by simulated annealing genetic algorithm (SAGA). But both GA and SA have their own features [6-11]. A newly improved SAGA is proposed in this work. By comprehensively considering the relationships between the changes of working parameters of the collecting head and cutting picks, forcing characteristics, and submarine microtopography, a numerical model for optimizing the working parameters is presented, which can provide theoretical basis for the mining operation in the seabed.

2 Optimization model of mining parameters

According to the characteristics of mining operations, the feed speed of the collecting head, the shaft height (can be converted to the corresponding excavation depth) and the rotation speed are set as parameters, to build an optimization function of the collecting head, targeting at the minimum energy consumption.

2.1 Objective function of mining parameter optimization

Based on the analysis of the influence of each parameter on the collecting head, a new parameter optimization model of the collecting head is built. And it is targeted at the optimal objective of minimum energy consumption and subjected to the collection ratio and interfusing ratio of mullock.

2.1.1 Mechanical modeling of pick

QIU [12] have detected the physical and mechanical properties of cobalt crust and bedrock. The study has shown that the cutting characteristic of the cobalt crust is similar to that of the moderate-intensity coal, and it exhibits a crushing mechanism. Therefore, we can utilize the mature coal-cutting theory to analyze the cutting and crushing process of cobalt crusts and bedrock. The difference is that the impact of sea water needs to be additionally considered for the latter.

When the pick cuts the cobalt crusts and the bedrock, its force consists of two parts: one is the cutting-pick crushing resistance, and the other is the force of seawater acting on the cutting-pick.

1) Pick-cutting crushing resistance

A large number of theoretical and experimental results of coal-cutting show that the pick resistance of cutting cobalt crust and bedrock can be represented as the comprehensive action of tangent force (F_t), axial force (F_a) and radial force (F_r):

     (1)

where A is the cutting impedance of cobalt crust, σ_y is its compressive strength, B is the brittleness index, l₀ is the intercept, b is the pick-edge width, f is the cutting drag coefficient, k_n is the stress-capacity factor, s_d is the cross- sectional area of tooth wear, h_c is the cutting thickness, the coefficient k=k₁?k₂?k₃?k₄, which is related to the cutting conditions of the collecting head, and e, c and d are empirical coefficients.

2) Force of seawater on pick

The movement of a pick in the seabed can be simplified as a rectangular rigid body rotating around the center, with the angular speed (ω) of 2π?n and the relative velocity of ocean current of v_h=v_q+v_w. Here, n is the rotational speed, and v_h, v_q and v_w denote the centerline horizontal resultant velocity of the collecting head, the horizontal speed of mining vehicle and the speed of undersea ocean currents, respectively. In Fig.1, force of a single pick is provided. Gravity (F_G) and seawater buoyancy (F_B) act on the centroid, and they can be calculated from F_B=V_T?ρ_w?g and F_G=V_T?ρ_s?g. The resultant force is

F₁=V_T?ρ_s?g+V_T?ρ_w?g                                                   (2)

where V_T is the volume of the pick, ρ_s and ρ_w are the densities of the seawater and the pick material, respectively. Through calculation, it can be drawn that the resistant force can be ignored because of the viscosity of seawater.

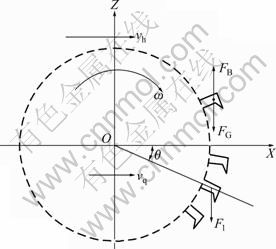
Fig.1 Resultant forces of pick

The total stress of the pick equals the sum of cutting resistance, F_G and F_B. And the total force in tangent, axial and radial directions (F_{t, t}, F_{a, t}, F_{r, t}) are as follows:

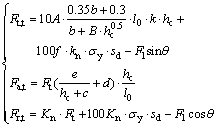                   (3)

2.1.2 Calculation modeling of collection capacity

Many studies have shown that the computation of the cobalt crust and bedrock collection capacity can be accurately made by applying digital elevation model [13]. According to the pose control instructions of the collecting head and the terrain elevation data measured in real time with microtopography detector, a digital elevation model is established based on the Delaunay triangulation. Adopting the TIN model, the total volume can be drawn from cumulating each irregular triangular cylinder volume. Taking arbitrary three-dimensional solid model shown in Fig.2 for example, a Delaunay triangle is constructed by connecting three closest points, such as ΔABC. The elevations of points A, B, C are supposed to be Z_A, Z_B, Z_C, respectively, and the height of the collecting head (i.e., the plane have been cut) is supposed to be Z. Then, the relevant collection capacity shall be the volume of the tri-prism ABCA′B′C′. However, there are difficulties in using thickness tester in seabed mining. It is usually believed that in a certain region, the thickness of cobalt crust is a fixed constant [14-15]. And according to the characteristic of microtopography, it can be classified into the following cases.

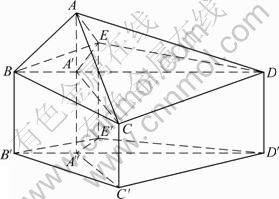
Fig.2 Schematic diagram of collection capacity calculation

Case 1: The elevations of the points of triangle are all above the cutting plane, and the total volume of collection is the tri-prism volume (V_T1):

                                          (4)

The volume of rock is

                                          (5)

where h₁, h₂ and h₃ are differences known in elevations; h₁=Z_A-Z, h₂=Z_B－Z and h₃=Z_C－Z, represent the elevation data, respectively. h₁-L, h₂-L and represent the corresponding bedrock elevation data, respectively; S denotes the base area; L denotes the cover thickness of the cobalt crust.

The volume of the cobalt crust is:

V_C1=S?L                                                       (6)

Correspondingly, the mass of rock, the mass of cobalt crusts and the total mass are respectively

m_R1=V_R1?ρ_R                                                                    (7)

m_C1=V_C1?ρ_C                                                                (8)

m_T1=m_R1+m_C1                                                                (9)

where ρ_C and ρ_R denote the densities of cobalt crust and rock respectively.

Case 2: The elevation of all vertices of microtopography triangle is above the cutting plane, and correspondingly the elevation of the two points of rock triangle is above the cutting plane.

The total collecting volume is the tri-prism volume (V_T1). The tri-prism, composed of bedrock, is divided into two parts by the cutting plane of collecting head, and correspondingly, the volume of the wedge (V_R2) collected is:

                           (10)

where   and  represent the maximum, median and minimum values of absolute values of h₁, h₂ and h₃, respectively.

The volume of cobalt crusts is

V_C12=V_T1-V_R2                                          (11)

Correspondingly, the mass of rock, the mass of cobalt crusts and the total mass are

m_R2=V_R2?ρ_R                                                                  (12)

m_C12=V_C12?ρ_C                                                              (13)

m_T12=m_R2+m_C12                                                           (14)

Case 3: The elevation of all vertices of microtopography triangle is above the cutting plane, and correspondingly, the elevation of the two points of rock triangle is below the cutting plane.

The total volume of collection is the tri-prism volume (V_T1). The tri-prism, composed of bedrock, is divided into two parts by the cutting plane of collecting head, and correspondingly, the volume of the triangular pyramid volume (V_R3) is

        (15)

The volume of cobalt crusts is

V_C13=V_T1-V_R3                                              (16)

Correspondingly, the mass of rock, the mass of cobalt crusts and the total mass are

m_R3=V_R3?ρ_R                                                                  (17)

m_C13=V_C13?ρ_C                                                              (18)

m_T13=m_R3+m_C13                                                           (19)

Case 4: The elevation of all vertices of microtopography triangle is above the cutting plane, and correspondingly, the elevation of all points of rock triangle is below the cutting plane.

In this case, the rock is not cut and the ore-rock collected is all cobalt crust, that is,

V_C14=V_T1                                                     (20)

m_T14=m_C14=V_T1?ρ_C                                              (21)

Case 5: The elevation of all vertices of microtopography triangle is above the cutting plane, and correspondingly, the elevation of the two points of rockbed triangle is below the cutting plane.

Both the two tri-prisms composed of the total microtopography and rock are divided into two parts by the cutting plane of collecting head, and correspondingly, the volumes of the wedges are V_T2 and V_R2, respectively:

                              (22)

Correspondingly, the volume of cobalt crusts is

V_C22=V_T2-V_R2                                             (23)

The mass of rock, the mass of cobalt crusts and the total mass are

m_R2=V_R2?ρ_R                                                                  (24)

m_C22=V_C22?ρ_C                                                              (25)

m_T22=m_R2+m_C22                                                           (26)

According to various possible cases listed above, the total collected mass of the spiral-cutting head crushing a range of ore-rock is

         (27)

Correspondingly, the mass of cobalt crusts is

         (28)

And the mass of rock (waste rock) is

     (29)

m_T=m_R+m_C                                          (30)

2.1.3 Modeling on specific energy consumption

The specific energy consumption of the spiral- cutting-type collecting head (w) is

                                             (31)

where W is the total energy consumption in cutting process, and G is the total weight of the broken cobalt crust and bedrock. W is equal to the integral of cutting power P in the working time t, and P is related to the rotation torque T_c of the collecting head. T_c is the resistance torque generated from the tangential resistance received by the pick of the collecting head in cutting the ore-rock, and

    (32)

All the above equations lead to

                                                     (33)

where m is the total number of cutting-picks, and r_i is the working radius of the i-th pick.

2.2 Optimum design of variables

The parameters in optimization objective function are constants with determined scope except k₁ and h_c. k₁ is related to h_c, while h_c is determined by specific submarine microtopography and working parameters (i.e. h, n and v). Therefore, the objective function above is related to submarine microtopography and working parameters of collecting head. And it is very important to know the total mass of collection capacity, collecting ratio and interfusing ratio of mullock which depend on h.

2.3 Constraints

2.3.1 Constraints of rotation speed and haulage speed

According to the theoretical analysis and the experimental results, the range of rotational speed is 20- 60 r/min. The ratio of v to n cannot be greater than twice of the working radius of the collecting head. The lower limit of v is 8.75 cm/s, its upper limit is 28.5 cm/s, and its range is v∈[8.5, 20.5]. Even though v is within this range, it cannot be guaranteed that the ratio of v to n is less than twice of the radius of the collecting head. So, in the penalty function of the optimization program, this condition is used as a penalty term. Once the condition cannot be satisfied, a great penalty will be met.

2.3.2 Establishment of constraints of interfusing ratio of mullock

The interfusing ratio of mullock (r) is

                                                           (34)

where m_R represents the total mass of bedrock, and m_T represents the total mass of bedrock and cobalt crust. The value of r varies according to different terrains, rather than being constant. The constraints of r are as follows: if the terrain height deviation is less than 7.5 cm, then r≤10%, otherwise, r≥20%.

2.3.3 Establishment of constraints of collection ratio

Collection ratio (q) is

                                                            (35)

where m_C is the total mass of collected cobalt crusts, and m is total amount of cobalt crusts in the mining area.

m_C is determined mainly by the surface area of microtopography in the mining area and the covering thickness of cobalt crust (L), that is,

m_C=S?L?ρ_C                                                        (36)

where S and ρ_C represent the surface area and the density of cobalt crust, respectively.

Digital elevation model (DEM) can be reconstructed on computer according to the Delaunay triangulation. The surface area can be divided into several triangles, and the value of it is equal to the sum of their respective surface areas. Each divided triangle of S is S_{i+1, j} or S_{i, j+1}, so the total superficial area is

                                        (37)

Therefore, q becomes

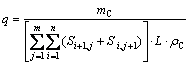                      (38)

And the constraint on q is

q≥90%                                                          (39)

The collection ratio and interfusing ratio of mullock are two main indexes in the mining of cobalt crusts as well as main constraints of the working parameters of the spiral-cutting collecting head. Their values only relate to the axis height. If the microtopography data are measured, the required elevation of the spiral-cutting collecting head will be determined by the crust thickness, interfusing ratio and collection ratio in a certain unchangeable thickness of cobalt crust. In general, an adequate maximum interfusing ratio is previously given, and then the collection ratio should be increased within this numerical range. That is to say, we should try to increase the cutting depth so that the interfusing ratio can be close to the predetermined value.

2.3.4 Constraints of axis height of collecting head

In order to ensure sufficient q and r within a certain range, h can only change along with the changes of microtopography. The upper limit value of h can be reached when the cobalt crust can just be cut by collecting head, while the lower limit value can be reached when the collection ratio is 100%.

3 Optimization algorithms

3.1 Simulated annealing genetic algorithm

Genetic algorithm (GA) is a search algorithm that adapts to the global optimization probability which simulates the hereditary and biological evolution process of creatures in nature. The specific implementation process of the GA is as follows: encoding and decoding, fitness function, setting initial species group, selection, crossover, variation and termination criterion [16]. Because of the variation and crossover constant probability in GA, some problems will appear, such as slow convergence speed and immaturity convergence [17-18]. Therefore, by use of the powerful global search capability of GA and the powerful partial search capability of SA, an improved SAGA is proposed. The improved SAGA integrates both of GA and SA effectively. And its main framework is the GA and some steps are connected with the SA. In the concrete design of the SAGA, real decoding is used, which improves the swapping operator, mutating operator and penalty functions and the constrained optimization problems are solved.

3.1.1 Real coding

In order to overcome the mapping errors existing in the binary coding, the real coding is used. This   method can unite phenotype and genotype together, which not only reduces the decoding process, but also speeds up the calculation rate. Real coding comprises each individual and their adaptive value into lines, so a number of individuals form a multi-line matrix, such as a function:

f(x₁, x₂, x₃)=x₁+x₂+x₃                                       (40)

[a₁, b₁, c₁], [a₂, b₂, c₂], …, [a_n, b_n, c_n] are respectively its n members, f(x₁, x₂, x₃) is the fitness calculation function of the corresponding member, with the decoding form as

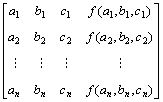
3.1.2 Selection and termination criterion

In the selection system, the sequencing method is applied, which ranks individuals of group according to the size of individual fitness, then distributes the designed probability table to individuals as each choosing probability. The probability calculation formula of each individual is

                                  (41)

where k is the positional number, n is the individual number in the group, q is the pressure parameter that controls group selection (when q is large, selection pressure is also large; otherwise, q is small), and P_k is the selection probability of the individual k.

The termination criterion applies duality principle: one is that iterations reach the maximum set value; the other is that the adaptive value of the function has no change for the required precision. The algorithm will stop no matter which one is failed to meet with.

3.1.3 Improvement of crossover operator

Considering the characteristics of the three operators of GA comprehensively, a new crossover operator is proposed, which can search both sides of the excellent individuals through a combination of the crossover operator and heuristic crossover operator. The mathematical description of the improved crossover operator is as follows: get any two individuals x₁ and x₂ from the group, whose fitnesses are f(x₁) and f(x₂), and when f(x₁)>f(x₂), two new individuals are produced:

           (42)

where λ₁ is a random number in [0, 1]; λ₂ is a random number in [0, u], u[0.5, 0.9]. When the value of u is 0.5, the new solution is far away form inferior solution; When u is 0.9, the new solution is close to inferior solution.

3.1.4 Improvement of simulated annealing and mutation operator

The GA sets powerful limited conditions before the execution of mutation operator, and the design reduces the generation of optimal solutions. In order to obtain much better individuals, it is proper to use wide-in and strict-out operator. That is to say, limited conditions are set after the execution of mutation operator, to expand the source of the generation of new solutions. But, whether it is chosen or not depends on the accuracy of new solution. Undoubtedly, this improvement helps the mutation operator to play a more important role and avoids the small probability mutation operator leaping over in most circulation process. Especially, in the later period of the search, when the population tends to be uniform, it is much easier to get the optimal solution with the wide-in and strict-out operator. In this work, Metropolis criterion is introduced as the constraint mechanism after the mutation operator. An operation of GA mutation operator is equivalent to a MapkoB chain. The overall frameworks of SAGA and GA are basically similar. Based on the characteristics of GA, SAGA can be combined with GA effectively by leading into the penalty function. In this work, Michalewicz and Attia’s penalty function method is improved accordingly, and the way is got to adjust the weight coefficients and penalty function.

Considering the following nonlinear programming problem:

1, 2, …, m₁

h_i(x)=0, i=m₁+1, …, m

The additional form of appropriate value function is

eval(x)=f(x)+p(t, x)

The penalty function consists of two parts: one is the variable penalty factor; the other is the punishment of violating constraints. The expression is

          (43)

where ρ(0) is a constant; c=0.95-0.99; r_i is the weighting coefficient, which can be set according to the magnitude of constrains; t is the evolution algebra; c^t is the variable penalty factor, called temperature. With the increase of t, the temperature is decreased gradually. It is similar to the annealing process, thus the penalties are increased gradually.

3.2 Simulated annealing genetic algorithm flowchart

The overall frameworks of the SAGA and the GA are basically similar. According to the established optimal design model and the SAGA above, the corresponding optimization program is developed by using the Matlab to get a solution. The SAGA flowchart is shown in Fig.3.

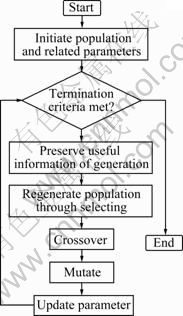
Fig.3 SAGA flowchart

4 Optimization results and linear regression analysis

When the microtopography data and the value range of the parameters designed in the optimizing program are input into a computer, the computer will autonomously do related calculations and optimization to the model. And the results will be shown on the main interface and the relevant data will be saved.

4.1 Optimization results of mining parameters

At the beginning, we should get as many details of submarine random complicated topography as possible [19] and figure out the distribution characteristics and laws of the big and tiny terrains of cobalt crusts. In the optimization process, according to the actual submarine microtopography, the microtopography of the seabed can be divided into 11 levels on the basis of the height difference (i.e., the distance between the highest point and the lowest one of the surface of the submarine topography). The height difference within 4.5 cm and  5.5 cm belongs to the second set. Topographic features can be described by elevation difference, roughness (i.e., the ratio of the terrain surface studied to its projection in the plane area), relative average height (i.e., the average difference between all the elevation values and the minimum elevation ones), and elevation mean square deviation. There are about 200 groups of the terrain data in each microtopography level. The roughness spacing is set as the basis, and the original data are selected based on the roughness. Ultimately, the topographic data in each level are determined.

After inputting the terrain data of the second set of submarine microtopography into the SAGA optimization program, the results are obtained. The selection of the SAGA control parameters are as follows: the population size is 20, the crossover probability is 1, the mutation probability is 1, the maximum evolutionary generations is 200, and the MapkoB chain length is 2. Table 1 gives parts of the optimization results of the second microtopography (r is the roughness, d is the relative average height, and a is the elevation mean square deviation).

Table 1 Parts of optimization results

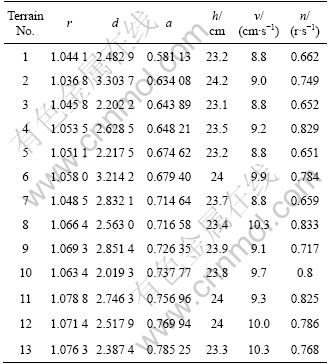
4.2 Regression analysis of results of mining parameters optimized

The optimization process mentioned above takes too much time, and it makes the response system so slow in the actual exploitation of mining so that discontinuous operation is resulted in. In order to shorten the response time, the calculation model for optimization results of mining parameters is established through the linear regression analysis of the optimization results. In actual work, the time-consuming iterative optimization process is changed into using the interpolation of linear equations directly to get a solution in accordance with the topographical features.

According to the multiple linear regression method, by the regression analysis of the hundreds of the second microtopography optimization results, the relationships between h, v, n and r, d, a are got respectively as

According to the terrain data measured by the detector and the regression model, the matching optimization results of working parameters of the collecting head are obtained quickly.

5 Conclusions

1) A new model is established to minimize the specific energy consumption, with the rotation speed, haulage speed and axis height of the collecting head as optimized parameters.

2) An improved simulated annealing genetic algorithm is proposed. It improves the crossover operator, and degenerates into a simulated annealing algorithm mutation operator. This algorithm is applied to optimize the mining parameters of the second-class submarine microtopography.

3) The regression model of optimizing the results is established, so that the methods, which cannot be applied to its long time processing of data, becomes feasible now.

References

[1] CHEN Rong-fa. Quiet rising of the new “Blue Enclosure Movement” [J]. Science In 24 Hours, 2006(1): 4-9. (in Chinese)

[2] YAMAZAKI T. Economic validation analyses of Japan’s proposed nodule, crust, and Kuroko-type SMS mining in 2006 [C]// OCEANS 2007. Vancouver, BC, INSDEC, 2007: 1-6.

[3] XIA Yin-min, NIE Si-jun. Optimize design of work parameters of cobalt-rich crust mining head [J]. Journal of Hunan University of Science and Technology, 2006: 1.

[4] QIN Xuan-yun, GUAN Ji-hong, REN Bo. Optimization methods of cutting depth in mining Co-rich crusts [J]. Journal of Central South University of Tehnology, 2007, 14(4): 595-599. (in Chinese)

[5] NAI Yi-nan, ZHANG Gang-yu. The optimization design of mechanical structure with fuzzy constraints [J]. Journal of Harbin University of Science and Technology, 2002, 7(5): 76-78. (in Chinese)

[6] FIGIELSKA E. A genetic algorithm and a simulated annealing algorithm combined with column generation technique for solving the problem of scheduling in the hybrid flowshop with additional resources [J]. Computers & Industrial Engineering, 2009, 56(1): 142-151.

[7] KERDCHUEN T, ONGSAKUL W. Optimal measurement placement for security constrained state estimation using hybrid genetic algorithm and simulated annealing [J]. European Transactions on Electrical Power, 2009,19(2): 173-185.

[8] CHEN Po-han, SHAHANDASHTI, SEYED MOHSEN. Hybrid of genetic algorithm and simulated annealing for multiple project scheduling with multiple resource constraints [J]. Automation in Construction, 2009, 18(4): 434-443.

[9] VASAN A, RAJU K S. Comparative analysis of simulated annealing, simulated quenching and genetic algorithms for optimal reservoir operation [J]. Applied Soft Computing, 2009, 9(1): 274-281.

[10] YOGESWARAN M, PONNAMBALAM S G, TIMARI M K. An efficient hybrid evolutionary heuristic using genetic algorithm and simulated annealing algorithm to solve machine loading problem in FMS [J]. International Journal of Production Research, 2009, 47(19): 5421-5448.

[11] SADEGHEIH A. Scheduling problem using genetic algorithm, simulated annealing and the effects of parameter values on GA performance [J]. Applied Mathematical Modelling, 2006. 30(2): 147-154.

[12] QIU Chang-jun. The study on the characteristics of cobalt crust and substrate rock for simulation [D]. Changsha: College of Mechanical and Electrical Engineering, Central South University, 2002. (in Chinese)

[13] WANG Li-hua, SHI Yi-min, WANG Wei-an. Calculation of earthwork based on TIN in analysis of underwater terrain [J]. Journal of Tongji University, 2004, 32(2): 234-236. (in Chinese)

[14] SHI Hai-lin. Study and analysis of the mining technology of deposit cobalt encrusted deposits in China (Part I) [J]. Express Information of Mining Industry, 2000(15): 1-2. (in Chinese)

[15] SHI Hai-lin. Study and analysis of the mining technology of deposit cobalt encrusted deposits in China (Part Ⅱ) [J]. Express Information of Mining Industry, 2000(16): 1-3. (in Chinese)

[16] SANAYE S, HAJABDOLLAHI H. Multi-objective optimization of rotary regenerator using genetic algorithm [J]. International Journal of Thermal Sciences, 2009, 48: 1967-1977.

[17] QIN Xuan-yun, BU Ying-yon. Optimization control of cut depth in the mining of ocean cobalt-rich based on GA [J]. Journal of Hunan University of Science & Technology: Natural Science Edition, 2005, 20(1): 17-20. (in Chinese)

[18] WANG Bin. WANG Sun-an, DU Hai-feng. Parameter optimization in industrial process control based on fuzzy genetic algorithm [J]. Journal of Xi’an Jiaotong University, 2004, 38(1): 56-59. (in Chinese)

[19] MA Wei-lin, JIN Xiang-long, CHEN Jian-lin. Geological characteristics of Co-rich, crusts, from the mid-pacific seamounts area [J]. Donghai Marine Science, 2002, 20(3): 11-23. (in Chinese)

(Edited by YANG Bing)

Foundation item: Project(50875265) supported by the National Natural Science Foundation of China; Project(20080440992) supported by the Postdoctoral Science Foundation of China; Project(2009SK3159) supported by the Technology Support Plan of Hunan Province, China

Received date: 2010-09-17; Accepted date: 2011-01-13

Corresponding author: XIA Yi-min, Professor, PhD; Tel: +86-731-88876926; E-mail: xiaymj@mail.csu.edu.cn