DOI: 10.11817/j.issn.1672-7207.2016.05.043
高速列车串行铝蜂窝吸能结构的轴向冲击动力学响应
丁叁叁1, 2,田爱琴2,李睿3,周伟3,许平3
(1. 北京交通大学 机械与电子控制工程学院,北京,100044;
2. 中国中车青岛四方机车车辆股份有限公司,山东 青岛,266111 ;
3. 中南大学 交通运输工程学院,轨道交通安全教育部重点实验室,湖南 长沙,410075)
摘要:研究高速列车串行铝蜂窝吸能结构在高速轴向冲击下的动力学性能。首先通过准静态试验对单块铝蜂窝的力学性能进行测试;然后通过高速冲击试验研究串行铝蜂窝的动力学特性;最后,采用参数辨识模型,得到串行铝蜂窝在高速轴向冲击下的刚度变化,并根据试验结果对串行铝蜂窝在高速轴向冲击下的偏移失稳现象进行分析。研究结果表明:串行铝蜂窝刚度系数的变化与铝蜂窝系统中隔板速度变化有密切关系,铝蜂窝开始变形时其刚度系数迅速变小,当各蜂窝前端隔板速度开始下降时蜂窝刚度系数曲线趋向平缓;串行铝蜂窝具有吸能量大、可实现变形模式可控,能够满足高速列车的冲击吸能量要求。
关键词:串行铝蜂窝;结构动力学模型;参数辨识方法;最小二乘法
中图分类号:U270.2 文献标志码:A 文章编号:1672-7207(2016)05-1782-06
Dynamic characteristics of serial honeycomb structure under
high-speed impact
DING Sansan1, 2, TIAN Aiqin2, LI Rui3, ZHOU Wei3, XU Ping3
(1. School of Mechanical, Electronic and Control Engineering, Beijing Jiaotong University, Beijing 100044, China;
2. China Railway Rolling Stock Corporation Qingdao Sifang Co., Ltd, Qingdao 266111, China;
3. Key Laboratory of Traffic Safety on Track of Ministry of Education, School of Traffic & Transportation Engineering, Central South University, Changsha 410075, China)
Abstract: Dynamic behavior of serial honeycomb under axial high-speed impact was studied. Mechanical behavior of single honeycomb block was tested in quasi-static experiments. And dynamic performance of serial honeycomb under axial high-speed impact was tested and studied. Rigidity change and destabilization of each honeycomb block were obtained and analyzed using parametric identification method. The results show that the rigidity change of serial honeycomb under axial high-speed impact is closely related to its deformation mode. The stiffness coefficient tends to decrease greatly when the honeycombs’ deformation starts, and then becomes smooth as velocity of forward isolation plates begins to drop. The serial-aluminum-honeycomb is of high energy absorption and controllable deformation pattern, which can satisfy the impact energy absorption requirements of high-speed train.
Key words: serial aluminum honeycomb; structural dynamics system; parametric identification method; least squares algorithm
铁路事故尤其是列车碰撞事故会造成重大人员伤亡和巨大经济损失。列车碰撞事故一旦发生,冲击能量会集中在列车司机室位置,因此,列车端部吸能装置的设计就显得尤为重要。随着列车运行速度的提高,对列车端部吸能装置的要求也越来越高,设计和优化合理的列车端部吸能装置已经成为列车耐撞性研究中的热点问题[1]。理想的吸能结构可以实现对冲击动能的可控吸收。复合蜂窝结构因其质量小、强度大、造价低等特点被广泛应用于民用建筑、航空航天、车辆轮船等领域,复合蜂窝的吸能能力是由材料、胞元形状及其排列形式决定的[2-8]。GIBSON等[9]阐述了蜂窝的结构与吸能特性之间的关系;WU等[10]研究了蜂窝在准静态与低速冲击条件下的力学特性;王中钢等[11-12]基于准静态试验和台车动态撞击实验,获取了铝蜂窝材料特性与吸能能力之间的关系,并得出铝蜂窝在低速冲击试验条件下吸能能力较准静态试验有所提升的结论。GREDIAC等[13-14]研究了蜂窝胞元之间的剪切作用,同时,LAURENT等[15]结合理论分析和数值仿真研究了蜂窝结构在各向载荷下的剪应力响应。ZHAO等[16-17]通过试验研究了不同胞元排列方式下的蜂窝塑性变形模式,并发现具有六角形薄壁胞元的蜂窝具有较高的吸能量。FAN等[18]结合试验和仿真对小型多层蜂窝结构并对其性能进行了研究,揭示了蜂窝结构的吸能量随蜂窝层数增加呈线性增长的趋势。上述研究主要针对单层结构蜂窝的吸能特性,然而受生产条件限制,单块铝蜂窝尺寸有限,不能满足高速列车发生碰撞时的大吸能量要求。因此,有必要将单层铝蜂窝结构组合串联起来,开展动态冲击作用下的吸能特性试验研究。另一方面,高速冲击试验中串行铝蜂窝容易出现偏移失稳现象,导致串行蜂窝变形模式和吸能效果不理想。因此,需要结合理论分析建立串行铝蜂窝的结构动力学模型,对串行铝蜂窝的变形模式、变形规律进行深入研究。本文作者采用增广递推最小二乘算法,对串行铝蜂窝的结构动力学模型中所有个体参数进行了辨识,明确了串行铝蜂窝在冲击试验中的吸能规律。
1 准静态压缩的铝蜂窝吸能特性
铝蜂窝结构静力试验在专用的INSTRON 1346材料力学性能试验系统进行。试验对象选取强度为5 MPa和10 MPa的铝蜂窝(材质为5052H18),加载速率为1 mm/min,加载温度为室温。表1所示为5 MPa和10 MPa强度蜂窝结构参数,图1所示为2种蜂窝的轴向压缩特性曲线。其中t,h和l分别为蜂窝胞元厚度、边长和高度;L,W和T分别为铝蜂窝块的长度、宽度和高度(厚度)。
表1 5 MPa和10 MPa铝蜂窝结构参数(T向正压)
Table 1 Aluminum honeycomb parameters with 5 MPa and 10 MPa energy capacity

图1 铝蜂窝压缩特性曲线
Fig. 1 Plateau stress-compression ratio curves of honeycombs
2 高速冲击的串联铝蜂窝吸能特性
由于单块铝蜂窝的吸能量有限,无法满足高速冲击时大小车的初动能吸能要求,因此,将多块铝蜂窝串联起来,通过高速冲击试验分析其动态纵向压缩 特性。
2.1 试验测点布置及数据获取
为精确分析串行铝蜂窝结构的撞击变形过程,在小车和隔板部位设置标识条,采用高速摄影完整记录小车、隔板的运动过程,通过基于变模板匹配和特征识别技术[19]的序列运动图像分析方法获取各个时刻的位移数据,最终对位移数据进行一阶和二阶求导分别得到小车及各隔板的冲击速度和加速度时程曲线。
高速摄影试验装置布置图如图2所示。图像采集装置采用NAC MEMRECAM HX-3高速摄像机(采样频率为10 kHz),布置于串行铝蜂窝上方,观测方向俯视朝向隔板和小车标识;序列图像分析的测点布置如图3所示,在小车和每块隔板上分别布置3个测点,采用模板匹配方法进行分析。
图2 高速摄影试验装置布置情况
Fig. 2 Arrangement of experimental instruments
图3 序列运动图像分析时测点布置情况
Fig. 3 Measuring points arrangement of sequence image analysis
选用截面积(长×宽)为466 mm×203 mm的5块铝蜂窝进行试验,首块蜂窝(1号蜂窝)强度为5 MPa,其余4块蜂窝强度为10 MPa;各蜂窝间隔板长×宽×厚为470 mm×205 mm×20 mm铝板,编号为隔板1~6,蜂窝与隔板通过环氧树脂胶黏结在一起;串行铝蜂窝安置于封闭轨道槽内,确保冲击试验中铝蜂窝只沿冲击方向发生变形;冲击端1 100 kg小车以35 m/s的初速度对串行铝蜂窝进行撞击,同时在冲击端加装50 mm橡胶板作为缓冲。
2.2 串行铝蜂窝位移、速度和加速度分析
冲击试验后串行蜂窝总变形量为603 mm,试验前后的串行铝蜂窝情况如图4所示。

图4 串行铝蜂窝冲击试验前后情况
Fig. 4 Series aluminum honeycomb before and after test
通过高速摄影序列图像运动分析可以得到小车和各隔板在冲击试验中的位移曲线,进而换算相邻隔板间的相对位移(如小车/隔板1代表小车和隔板1之间的相对位移,即蜂窝1的压缩量,依此类推)。对各隔板位移进行一阶和二阶求导,得出小车及各隔板在冲击试验中的速度和加速度曲线。小车与临近隔板以及相邻隔板之间的相对位移、小车与各隔板的速度和加速度曲线如图5所示。
由图5可得到如下规律:
1) 冲击过程中首块5 MPa强度铝蜂窝先发生变形,相邻10 MPa强度蜂窝依次变形;
2) 蜂窝开始压缩时,其前端隔板(朝撞击小车方向)速度迅速增大,与后端隔板(朝撞击墙方向)间形成速度差导致蜂窝发生变形;
3) 在压缩过程中,第1块隔板最先出现加速度峰值,由于串行蜂窝系统与约束轨道之间间隙较小,第1块蜂窝压缩膨胀使得轨道与整个吸能结构之间的摩擦力增大,同时,第2块隔板之后的结构对该隔板产生了1个与其运动方向相反的反作用力,因此,第2块隔板在9.5 ms出现了与运动方向相反的加速度峰值;
图5 串行铝蜂窝系统中小车和各隔板的相对位移、速度和加速度曲线
Fig. 5 Displacement, velocity and acceleration curve of mass blocks and isolation boards in series aluminum honeycomb system
4) 在整个冲击试验中,小车速度均匀下降,串行铝蜂窝系统吸能比较稳定,各蜂窝变形量均不相同,其中第1块蜂窝变形量最大。
2.3 串行铝蜂窝能量吸收分析
冲击试验中,小车的初动能为673.75 kJ,其中80%能量由串行蜂窝率吸收。表2所示为串行铝蜂窝系统中各蜂窝压缩量数据和吸能量估计。其中试验平台力是由力传感器检测得到。
表2 串行铝蜂窝压缩量和估算吸能量
Table 2 Compression and estimated energy absorption of series aluminum honeycomb
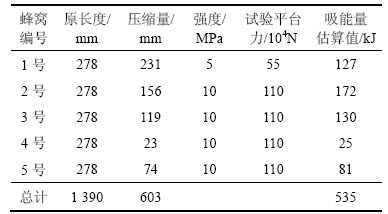
由表2可知:在冲击试验中,串行铝蜂窝系统第1块蜂窝压缩量最大,第2块蜂窝吸能量最大。
3 基于参数辨识方法对串联铝蜂窝在动态冲击下的压缩特性分析
3.1 串行铝蜂窝动力学模型
对于自由振动的线性单自由度系统,其动力学模型可由下式描述:
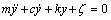 (1)
(1)
其中:y为质点位移;m为质量;c为阻尼系数;k为弹性体刚度系数;ζ为残差,包含了输出噪声和参数估计误差。
本文的串行铝蜂窝系统是一个自由振动的非线性多自由度系统。离散时间域的非线性单自由度系统中,每个时间点可以近似用线性系统的动力学方程来表示。通过试验数据采集系统获取准确的质点位移时域离散数据,对于周期性采样点ti,采用向后差分法将导数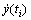 和
和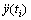 近似为离散形式,将这些近似关系式带入离散时间动力学模型,整理后可得[16-18]:
近似为离散形式,将这些近似关系式带入离散时间动力学模型,整理后可得[16-18]:
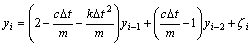 (2)
(2)
对于串行铝蜂窝吸能系统,在冲击试验中使用一辆具有初速度的小车对其进行冲击,冲击端使用橡胶板作为缓冲,使用隔板将各块铝蜂窝分隔,小车和各隔板的动力学模型描述如下式所示。
 (3)
(3)
其中:y,m和c分别为小车以及各隔板位移、质量和阻尼系数;k1为橡胶刚度系数;k2~kn为各铝蜂窝刚度系数,随着冲击过程的进行,刚度系数在每个离散的时间点上有所变化;ζi为残差。
3.2 最小二乘参数辨识方法
串行铝蜂窝动力学模型通过离散化处理,已转变为线性函数,通过小车和隔板的位移数据即可确定串行铝蜂窝动力学模型中的所有参数。对于已采集到的小车和各隔板位移数据,需要考虑其测量噪声。
最小二乘估计方法能够找到可以满足使误差函数最小的参数,误差函数表示为
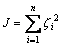 (4)
(4)
串行铝蜂窝动力学模型的矩阵形式为
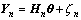 (5)
(5)
其中:输入矩阵Hn为
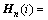
 (6)
(6)
参数矩阵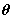 为
为
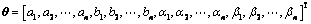 (7)
(7)
误差函数为
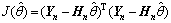 (8)
(8)
根据极值定理,求得参数矩阵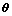 的最小二乘估计为[20-21]
的最小二乘估计为[20-21]
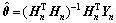 (9)
(9)
3.3 吸能特性和动力学模型参数辨识
针对串行铝蜂窝系统中小车和各隔板在冲击试验中的位移数据,在MATLAB中使用最小二乘法对其进行参数辨识。如图6所示,由于串联铝蜂窝系统中第3块铝蜂窝及其前端隔板在压缩过程第17 ms发生了偏斜,将整个试验过程划分为均匀变形过程和非均匀变形过程,对其动态特性进行参数辨识。

图6 串联铝蜂窝在压缩过程中的偏斜情况
Fig. 6 Deflection of series aluminum honeycomb system under high-speed axial impact
基于最小二乘辨识方法,可以得到式(3)中各项系数结果,令
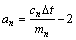 ,
,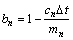 (10)
(10)
 ,
,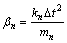 (11)
(11)
式中:mn和cn分别为第n块隔板的质量和阻尼系数(n=0代表小车);kn为第n块铝蜂窝的刚度系数。
在冲击试验中,串行铝蜂窝系统动力学模型中各参数略有波动,分段对各参数进行分析,结果如表3所示。
表3 串行铝蜂窝模型摩擦力参数分段分析
Table 3 Sectionalized analysis on friction of each honeycomb
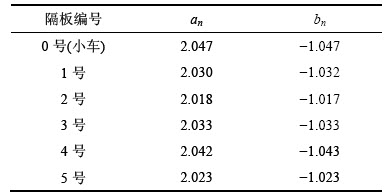
串行铝蜂窝动力学模型中的阻尼系数和刚度系数是采样间隔△t的函数,即为高速摄影采样间隔,取△t=0.1 ms。由表3可知:串行铝蜂窝吸能过程中an和bn略有波动,但其规律与两者的数学关系式相吻合。
对于串行铝蜂窝的刚度系数kn,可以通过式(10)计算得到。绘制缓冲橡胶、各块蜂窝的刚度系数曲线如图7所示(其中,k0为橡胶刚度,k1为强度5 MPa蜂窝刚度系数,k2~k5为强度10 MPa时第2~5块蜂窝刚度系数)。
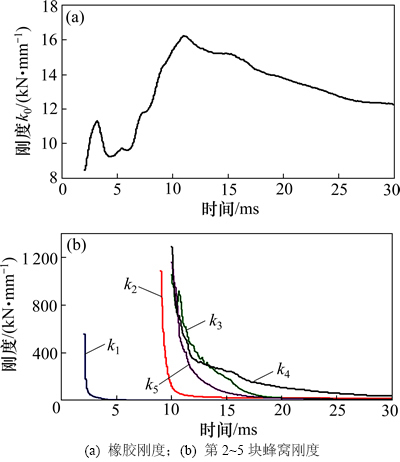
图7 串行铝蜂窝系统中橡胶和各蜂窝刚度参数辨识曲线
Fig. 7 Calculated stiffness of each honeycomb using parameter identification method
由图7可知:铝蜂窝在吸能过程中刚度系数迅速变小,其刚度系数曲线趋向平缓时该蜂窝前端隔板速度开始下降;5 MPa蜂窝的最大刚度约为5.5×108 kg/s2,10 MPa蜂窝的最大刚度约为1.1×109 kg/s2。可见,在35 m/s高速冲击试验中,串行铝蜂窝系统中各蜂窝吸能稳定、吸能情况良好,第2块蜂窝强度比第1块的大,位置靠前,因此吸能量最大;第5块蜂窝先于第4块蜂窝发生变形,并且蜂窝刚度较第4块弱,因此,其吸能量比第4块蜂窝的大。
4 结论
1) 串行铝蜂窝吸能装置在高速冲击试验中吸能良好,整个过程中小车与各隔板位移、速度、加速度变化符合运动学规律。
2) 串行铝蜂窝刚度系数变化与铝蜂窝系统中隔板速度变化有密切的关系,铝蜂窝在参与吸能过程中刚度系数迅速变小,该蜂窝前端隔板速度开始下降时其刚度系数曲线趋向平缓。
3) 最小二乘法是辨识结构动力学模型的一种非常有效的方法,能够辨识出结构动力学模型中的相关重要参数,对串行铝蜂窝吸能过程的分析提供科学依据。
参考文献:
[1] 高广军, 姚松. 车辆薄壁结构撞击吸能特性研究[J]. 铁道机车车辆, 2002(2): 8-10.
GAO Guanjun, YAO Song. Research on energy absorbation attribute in collision of thin-shell structure between trains[J]. Railway Locomotive & Car, 2002(2): 8-10
[2] ESKANDARIAN A, MARZOUGUI D, BEDEWI N E. Finite element model and validation of a surrogate crash test vehicle for impacts with roadside objects[J]. Int J Crashworthiness, 1997, 2(3): 239-258.
[3] 王闯, 刘荣强, 邓宗全, 等. 铝蜂窝结构的冲击动力学性能的试验和数值研究[J]. 振动与冲击, 2008, 27(11): 56-62.
WANG Chuang, LIU Rongqiang, DENG Zongquan, et al. Experimental and numerical studies on aluminum honeycomb structure with various cell specifications under impact loading[J]. Journal of Vibration and Shock, 2008, 27(11): 56-62.
[4] 李萌, 刘荣强, 罗昌杰, 等. 铝蜂窝串联缓冲结构静态压缩仿真和试验研究[J]. 振动与冲击, 2013, 32(9): 50-56.
LI Meng, LIU Rongqaign, LUO Changjie, et al. Numerical and experimental analyses on series aluminum honeycomb structures under quasi-static load[J]. Journal of Vibration and Shock, 2013, 32(9): 50-56.
[5] YAMASHITA M. Impact behavior of honeycomb structures with various cell specifications: numerical simulation and experiment [J]. Int J Impact Eng, 2005, 32(1/2/3/4): 618-630.
[6] HOU S, LI Q, LONG S, et al. Design optimization of regular hexagonal thin-walled columns with crashworthiness criteria[J]. Finite Elem Anal Des, 2007, 43(6/7): 555-565.
[7] WORDEN K, TOMLINSON G R. Nonlinearity in structural dynamics[M]. Beijing: China Machine Press, 2012: 187-198.
[8] CRICR G, PERRELLA M, CAL
G, PERRELLA M, CAL C. Honeycomb failure processes under in-plane loading[J]. Composites: Part B, 2013, 45: 1079-1090.
C. Honeycomb failure processes under in-plane loading[J]. Composites: Part B, 2013, 45: 1079-1090.
[9] GIBSON L J, ASHBY M F. Cellular solids: Structures and properties[M]. 2nd ed. Cambridge: Cambridge University Press, 1997: 93-158.
[10] WU E, WU S. Axial crush of metallic honeycombs[J]. Int J Impact Eng, 1997, 19(3): 439-456.
[11] 王中钢, 鲁寨军. 铝蜂窝异面压缩吸能特性试验评估[J]. 中南大学学报(自然科学版), 2013, 44(3): 1246-1251.
WANG Zhonggang, LU Zhaijun. Experimental assessment on energy absorption property of aluminum honeycomb under out-of-plane compression[J]. Journal of Central South University (Science and Technology), 2013, 44(3): 1246-1251.
[12] WANG Zhonggang, TIAN Hongqi, LU Zhaijun, et al. High-speed axial impact of aluminum honeycomb- Experiments and simulations[J]. Composite: Part B. 2014, 56: 1-8.
[13] GREDIAC M. A finite element study of the transverse shear in honeycomb cores[J]. International Journal of Solids and Structures, 1993, 30(13): 1777-1788.
[14] QIAO Pizhong, FAN Wei, DAVALOSB J F, et al. Optimization of transverse shear moduli for composite honeycomb cores[J]. Composite Structures, 2008, 85(3): 265-274.
[15] LAURENT W, STEFAN M, DANIELE W, et al. Shear stresses in honeycomb sandwich plates: analytical solution, finite element method and experimental verification[J]. Journal of Sandwich Structures and Materials, 2012, 14(4): 449-468.
[16] ZHAO Long, ZHENG Qing, FAN Hualin, et al. Hierarchical composite honeycombs[J]. Materials and Design, 2012, 40: 124-129.
[17] ZHENG Jingjing, ZHAO Long, FAN Hualin. Energy absorption of hierarchical woven lattice composites[J]. Composite: Part B, 2012, 43: 1516-1522.
[18] FAN H L, ZENG T, FANG D N, et al. Mechanics of advances fiber reinforces lattice composites[J]. Arch Mech Sin, 2010, 26(6): 825-835
[19] 许平, 姚曙光. 列车部件撞击序列图像运动分析方法[J]. 交通运输工程学报, 2006, 6(1): 20-24.
XU Ping, YAO Shuguang. Motion analysis method of series images for train component crash[J]. Journal of Traffic and Transportation Engineering, 2006, 6(1): 20-24.
[20] 刘金琨, 沈晓蓉, 赵龙. 系统辨识理论及MATLAB仿真[M]. 北京: 电子工业出版社, 2013: 31-57.
LIU Jinkun, SHEN Xiaorong, ZHAO Long. System identification theory and MATLAB simulation[M]. Beijing: Electronics Industry Press, 2013: 31-57.
[21] 丁峰. 系统辨识新论[M]. 北京: 科学出版社, 2013: 1-33.
DING Feng. A new system identification theory[M]. Beijing: Science Press, 2013: 1-33.
(编辑 杨幼平)
收稿日期:2015-10-23;修回日期:2015-12-28
基金项目(Foundation item):国家科技支撑计划项目(2015BAG12B01);国家自然科学基金资助项目(U1334208);中国铁路总公司研究开发计划项目(2013G006) (Project(2015BAG12B01) supported by the National Key Technology Support Program; Project(U1334208) supported by the National Natural Science Foundation of China; Project(2013G006) supported by the Research and Development Program of China Railway Corporation)
通信作者:丁叁叁,教授级高级工程师,从事列车撞击动力学研究;E-mail: dingsansan123@sina.com