文章编号：1004-0609(2014)01-0097-07

金属基复合材料微观组织结构的计算机模拟

张  赋，李旭东

(兰州理工大学 甘肃省有色金属新材料省部共建国家重点实验室，兰州 730050)

摘  要：介绍一种用于金属基复合材料微观组织结构的计算模拟与可视化表征的有效方法。着重阐述了利用Laguerre图构造算法、Monto-Carlo方法及Laguerre窗口技术构造金属基复合材料微结构的技术流程，说明如何通过改变、控制、组合不同种类的微结构模块，产生更加复杂的金属基复合材料微结构的方法。在此基础上，根据模块化设计思路，设计并开发仿真软件VisualTPS以作为金属基复合材料微观组织结构的计算机设计、性能导向型研究体系的工具。

关键词：金属基复合材料；微观组织；各向异性；Laguerre图；可视化仿真

中图分类号：TB331　　     文献标志码：A

Computer simulation of microstructure for metal matrix composites

ZHANG Fu, LI Xu-dong

(State Key Laboratory of Gansu Advanced Non-ferrous Metal Materials,

Lanzhou University of Technology, Lanzhou 730050, China)

Abstract: A method for the metal matrix composite microstructure simulation and visualization was introduced. A set of microstructures for composite materials was constructed by using the algorithm of Laguerre diagram, Monto-Carlo method and Laguerre Windows technique. The modularized microstructure can be altered, manipulated and combined so as to create more complex microstructure. Based on the modular design ideas, the software, namely VisualTPS, was developed as a tool for the metal matrix composite microstructure computer design and performance-oriented research.

Key words: metal matrix composite; microstructure; anisotropy; Laguerre diagram; visualized simulation

材料的性能不仅依赖于材料的化学成分，而且在很大程度上取决于材料的微观组织结构。复合材料微观组织结构的计算机模拟与表征已经成为微观组织结构“性能导向型”设计的重要工具。通过各种算法设计构筑复合材料的微观组织结构，提供一个可信赖的“代表性体积单元(RVE)”，对复合材料细观乃至微观尺度的性能预测、失效行为的推演有着重要意义^[1-3]。KUMAR等^[4-5]采用Voronoi算法建立的多晶体几何模型从统计学意义上模拟了微观组织结构的任意性，并将其应用于细观力学分析。此后，AURENHAMMER^[6]，LAUTENSACK^[7]，FAN等^[8]和COSTER等^[9]提出了较Voronoi算法更准确、更具设计性的Laguerre算法，用于多胞材料、多孔材料微结构的模拟。GHOSH等^[10-11]对金属基颗粒增强复合材料微观组织结构进行了表征，并对其力学性能进行了预测。在国内，LI^[12]和李旭东^[13-15]以Voronoi算法为基础开发针对二维多晶体基异质性材料微观组织结构的计算机可视化、系统化仿真的软件ProDesign。但针对三维金属基复合材料微观组织结构系统化、模块化仿真的工作还尚未形成完整的体系。本文作者采用从统计意义上更加准确的Laguerre图构造三维多晶体基体，通过定量描述每个第二相组成物几何与基体组成物几何之间以及与相邻第二相组成物几何之间的空间位置关系，对不同类型的复合材料进行相应的算法流程设计，实现复合材料微观组织结构的计算机表征与模块化设计，用于复合材料宏/细观性能响应的力学模型计算。

1  Laguerre图

Laguerre图的胞体结构在几何形貌和拓扑结构上与某些材料微观组织结构十分相似，通过选定合适的尺度，使得微结构达到统计学意义上的平均性质，可以获得具有与材料组织、相结构等各种组成物十分近似的材料微观组织结构的几何模型。

在d维欧氏空间中，已知点集P={P₁(p₁，w₁)，P₂(p₂，w₂)，…，P_n(p_n，w_n)}，其中每个点P_i均被赋予一个权值w_i。对于点和，定义为点p到权值点P_i的幂距离。将到点P_i的幂距离不大于到其他任意权值点的幂距离所构成的集合称为点p_i关联的Laguerre单胞，其单胞的数学定义如下：

             (1)

由每个权值点所关联的单胞集合构成权值点集的Laguerre图。从Laguerre单胞的数学定义可以看出：单胞的形成受点集空间位置与权值分布的共同影响。特别地，若权值点集中所有点的权值大小均相等，则Laguerre单胞退化为Voronoi单胞。图1所示为权值大小随机分布的二维Laguerre图。

图1  二维随机Laguerre图

Fig. 1  2D random Laguerre diagram

2  组成物取向

含有统一晶体学取向的区域被认为是一个独立的复合材料组成物^[16]。本文作者利用随机数产生器在Euler空间里任意取值或按指定规律(如定向凝固)来模拟组成物的取向分布。

以椭圆短纤维增强的复合材料为例，其微观组织结构不仅包含空间分布的任意多面体的晶粒与其晶体学取向，而且还包含空间分布的椭球形短纤维及其空间取向。对于晶粒的晶体学取向，采用Euler空间Ω中的3个区间角(极角、方位角和旋转角)来描述，如图2(a)所示。对于第i个任意取向的晶粒，局部坐标(x_i，y_i，z_i)与参考坐标系(x，y，z)的关系如下：

                    (2)

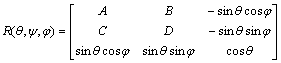 (3)

式中：A=cos θcos ψcos φ-sin ψsin φ；B=cos θcos ψcos φ+cos ψsin φ；C=-cos θcos ψsin φ-sin ψcos φ；D=-cos θsin ψ sin φ+cos ψcos φ。

根据式(2)和(3)，通过一系列的坐标变换，可以用整体坐标系下的一组空间坐标来描述某一晶粒的取向。

图2  组成物取向的表征

Fig. 2  Orientation of composite constituents

图3  多晶体材料微的结构构造

Fig. 3  Microstructure construction of polycrystalline material

同样，短纤维被认为是拥有各自空间取向的几何区域。对于在Euler空间中相对整体参考坐标下的短纤维的空间取向也采用3个区间角(α，β，γ)来表征，通过坐标变化亦可用整体坐标系下的一组空间坐标来描述，实现增强相取向信息的表征。

3  多晶体集合的计算

多晶体材料微观组织结构可以采用Laguerre图的胞体结构来表征，且仅考虑理想晶体的情况，并不涉及晶体缺陷的表征。根据Laguerre图的性质可知，多晶体材料晶粒的尺寸、形状及分布规律取决于形核种子点集，而每个形核种子的特征由点的空间位置和权值大小共同控制。因此通过对形核种子点集进行控制与设计，以此构造Laguerre多晶体几何模型，实现对多晶体材料微观组织结构设计。

一般采用球填充过程来完成对形核种子点集的设计。FAN等^[8]给出了球填充点集下将Voronoi模型扩展为Laguerre模型的多晶体材料微结构构造方法。本研究直接采用Laguerre图构造算法，并结合球填充过程进行多种设计以生成不同分布特征的多晶体材料微观组织结构。

球填充过程是在指定空间按一定体积分数填充球体，使得球体之间互不接触。将每个球体的球心坐标与半径的平方作为一个权值点。在给定区域内，根据给定的平均晶粒尺寸及分布参数，可以计算出形核数量N、构造出形核种子点的权值分布情况，同时采用球填充过程对形核种子点集进行空间定位，完成对多晶体材料微结构的模型拟合，最后利用

Laguerre算法获得对应的胞体几何结构，并将胞体结构中随机形状的P面体代表晶粒，这个P面体中没有优先的晶粒生长方向。图3(a)和(b)分别展示了形核种子点集按随机分布与球填充分布所构造的多晶体材料微观组织结构。

对于某些多晶体材料，例如表层晶粒细化的微观组织结构，其晶粒尺寸沿某一方向为梯度分布。要产生这一类具有梯度分布的多晶体材料微观组织结构，可以利用球填充过程在给定区域内产生两类具有不同的平均晶粒尺寸、任意分布的形核集合(或有预定分布的形核)。之后，将两组原始的形核集合合并成为一组初始形核，以此构造生成Laguerre图。图3(c)所示为计算机模拟的多晶体表层具有细化晶粒的微观组织结构样品。

在传统的晶粒模型中，晶界在二维空间里被认为是一条直线，而在三维空间里被认为是一个平面。但是，当晶粒尺寸减小到一定程度时，晶界不能够再被处理成直线或平面，因此，晶粒尺寸的大幅下降后必须要考虑晶界的物理与几何特征及其性能。为了反映由于晶粒尺寸超细化而使晶界的几何作用相对显著的影响，通过将Laguerre晶胞的顶点坐标按照晶界的平均尺寸比例进行空间缩放变换，从而得到细化晶粒的几何形状与晶界的几何形状，如图3(d)所示。所有这些被缩小比例的Laguerre晶胞共同组成一个超细晶粒组织结构。经过这种处理以后的晶粒平均尺寸会有所缩小，因此，需要按晶界的缩放比例对初始晶粒的平均尺寸进行放大，再进行上述模拟过程，此时由超细化晶粒组成的实际多晶体微观组织结构在晶粒尺寸上的偏差所造成的影响已不再显著。

对于多晶体材料微结构中组成物含有多相的情况，如纳米复合材料微结构^[17]，每一相组成物的晶粒平均粒径、分布特征、晶体学取向等不相同，其差异程度将影响材料的性能指标，因此需要准确地模拟每一相组成物的特征。类似于模拟表层细化的多晶体材料微结构，构造多类含有指定分布的形核集合，以此进行球填充过程下的Laguerre晶胞构造；同时，对单胞进行跟踪识别，获得每一类形核对应产生的晶粒，作为多相多晶体材料微结构组成物的一相。图3(e)展示了一个多相多晶体材料微观组织结构的几何模型。

4  第二相组成物的表征

本文作者对第二相组成物的最终形貌进行表征，因此并不涉及第二相的生长过程。同时，并未从几何角度来定量表征界面，而是在构造第二相组成物时，将第二相组成物与基体之间的界面简化为与基体材料完美结合的一种简单边界，这样就可以表征由于第二相组成物分布的任意性而引起的几何效应与取向效应。为了可视化展示，微观组织结构中组成物的相对尺寸都进行调整。以下对复合材料微观组织结构仿真的基本模块进行阐述，并重点讨论利用基本设计模块构筑更加复杂的复合材料微观组织结构。

4.1  随机分布

对于第二相组成物随机分散在基体材料中的情况，这里以短纤维增强物为例来说明。一个短纤维分布系统不仅取决于短纤维的体积分数，而且取决于短纤维与短纤维之间的空间距离，同时还需考虑短纤维的取向分布规律。短纤维的体积分数与短纤维之间的空间距离将共同控制短纤维的稀疏或密集程度，而短纤维之间的空间距离将决定短纤维是否桥接。如果在计算机产生的复合材料样品中不允许短纤维桥接，则每个短纤维必须被放置在给定的区域内，并且短纤维之间的距离一定要大于预先设定的最小距离容限。

在三维空间中短纤维可以由椭球体代表。在给定区域内运用伪随机算法任意布置短纤维，不仅要保证全部的短纤维占据所给定的体积分数，而且要保证短纤维之间的空间位置关系。从技术角度看，采用基于Monte-Carlo迭代法的计算机模拟程序，可以使计算机产生的短纤维分布(包括纤维长度和直径分布，数量密度，体积分数和短纤维的空间排布)与一个真实短纤维增强的复合材料中的增强物分布等效。图4(a)所示为一个典型的短纤维密集分布的复合材料微观组织结构模块。

图4  各类复合材料微观组织结构

Fig. 4  Microstructure construction of different types composite material

在一个真实的复合材料微观组织结构内，增强物的尺寸和形状一般都是不规则的，且增强物的取向也不同。为了体现这种不规则现象对复合材料性能的影响，就要构筑一个由不同尺寸、不同相、不同取向分布增强物的复合材料微观组织结构模块。图4(b)展示了晶须增强的复合材料微观组织结构模块。图4(c)展示由3种不同相增强物增强的复杂型复合材料微观组织结构模块。图4(d)展示了短纤维增强物选择性分布的复合材料微观组织结构模块。

在工程上通常应用由交错型布置的纤维增强的复合材料。交错型纤维增强的复合材料微观组织结构模块可以通过取消限制相邻纤维之间的最短距离来获得。图4(e)所示为上面所说的这样一个微观组织结构模块，其分布的短纤维出现了拼接。这种微观组织结构更为符合实际的复合材料。对于某些复合材料微观组织结构，增强物只能分布在晶界上，模拟这种结构需要为Laguerre多面体的每个面确定表达式，以此来对沿多面体边界呈任意分布的每个颗粒进行定位。图4(f)所示为短纤维分布在晶界上的情况。

4.2  梯度及层状结构

模拟增强物在基体材料中按梯度性分布所采用的方法是将基体材料所在区域分割为几个子区域，再将具有任意性或优先性取向的增强物分布在各个子区域中，并保证所有子区域中分布的增强物的数量总和与预先确定的增强物的体积分数相当。图5(a)给出了具有梯度分布的短纤维增强复合材料的计算机样品。

层状复合材料的微观组织结构一般是比较复杂的。采用计算机构筑层状复合材料的微观组织结构的方法与构筑梯度性分布复合材料的方法类似。本研究考虑复合材料中两类典型呈层状排列的微观组织结构。第一类是不同类型的增强物以分层分布于基体材料中的微观组织结构内；第二类是“三明治”结构。图5(b)所示为一个示意型的增强物以分层分布于基体材料内的微观组织结构，3类不同类型的增强物分层分布于基体材料微观组织结构的不同区域。图5(c)所示为一个示意型的“三明治”结构，这类复合材料的微观组织结构可以看成是不同类型的复合材料微观组织结构的复合。

4.3  非均匀分布

事实上对于一个实际的颗粒(或短纤维)增强复合材料来说，增强物会在微观组织结构内呈极不规则的分布，然而颗粒既不会按一定的序列分布，也不会按绝对任意的方式分布。这种增强物的不均匀分布可能存在于工业生产的复合材料中。在一个实际复合材料微观组织结构中，将出现增强物聚集区域与增强物稀疏区域，这将影响复合材料的性能，并使不同的样品具有不同的性能。其次，如图6(a)所示，具有块状增强物的复合材料微观组织结构也呈现出增强物聚集区与增强物稀疏区。

图5  复合材料的层状及复杂型微观组织结构

Fig. 5  Microstructure construction of graded and complex composite material

图6  块体增强及纤维团簇分布的复合材料微观组织结构

Fig. 6  Microstructure construction of composite material with block enhanced (a) and reinforcement clusters distribution (b)

对于增强物聚集区，本研究采用的模拟流程是采用任意分布的“Laguerre窗口”技术来实现的。首先在给定区域内根据多晶体材料的平均晶粒尺寸及分布构造出基体的Laguerre晶胞。同时，在此区域内产生第二组Laguerre图形，该图形将此区域划分为“Laguerre窗口”。“Laguerre窗口”的平均尺寸应该足够大，以便使每一个增强物聚团区可以被包含在“Laguerre窗口”内。将第二个Laguerre图形中随机选定一定数量的窗口，并将给定尺寸的增强物分布于其中，以形成若干个团簇，从而模拟位置和形状都不规则的团簇对材料性能所产生的效应。依据一个给定的窗口内增强物在当地的体积分数，可以计算出分布在每个团簇中的增强物的数量。需要明确的是，不仅每个窗口内增强物在局部范围内的体积分数不同，而且单个“Laguerre 窗口”内组成团簇增强物的数量既要与每个窗口范围内当地的体积分数相一致，又不能超出预先给定的模块内增强物总的体积分数。分散分布、没有形成团簇的增强物以统一的当地体积分数分布于其余的“Laguerre窗口”内，以达到模块内所给定的增强物总的体积分数。统一的当地体积分数可以用下式表示：

                 (4)

式中：V^D表示模块体积；V^A代表已经产生的增强物团簇所占的总体积；代表给定的增强物在模块中所占据的总的体积分数；表示形成团簇的增强物所占据的体积分数；而表示分散分布的、未形成团簇的增强物在其余的“Laguerre窗口”内所应有、统一的体积分数。图6(b)所示为运用“Laguerre窗口”技术生成的纤维增强物团聚分布的复合材料微观组织结构的计算机样品。

5  仿真软件

在实现金属基复合材料微观组织结构构造算法的基础上，本研究开发了相应的仿真软件VirtualTPS，旨在搭建“材料微结构－可视化演示－力学建模”之间“沟通”的桥梁，为金属基复合材料微观组织结构的可视化设计、结构－性能关系研究提供基础性的仿真工具。

仿真软件VirtualTPS采用Python语言将Laguerre图算法、球填充算法、Monto-carlo算法等内核代码进行集成，同时结合PyOpenGL编程，用于仿真结果的可视化显示，并利用wxPython模块开发相应的图形用户界面（GUI），为用户提供一个简洁、友好的交互界面。 软件主要实现了以下几个模块的功能：多晶体材料微结构设计与构造、第二相组成物构造、取向分布生成、仿真结果可视化。

6  结论

1) 软件VisualTPS以Laguerre图算法为基础，采用不同的设计流程构造出多种不同类型的多晶体材料微观组织结构，如等轴晶材料、表面细化材料、纳米晶体材料、多相多晶体材料等，并以此作为复合材料微观组织结构中的基体相。对于增强相的表征，软件结合Monto-Carlo算法设计，定量描述组成物之间的空间位置关系。在完成复合材料组成物几何结构的模拟之后，软件引入晶粒及增强物取向的各向异性行为，实现对复合材料微观组织结构几何信息、织构信息的完整表征。

2) 在软件基本模块设计中，采用子区域分割法及“Laguerre窗口”技术，可用于模拟块体增强复合材料、梯度性复合材料、层状复合材料的微观组织结构，也可以用于表征增强物团聚分布的复合材料微观组织结构。同时，利用模块组合的手段，还可以构造出更加复杂的、多种多样的复合材料微观组织结构。

3) 运用软件所构筑的复合材料微观组织结构中组成物的几何形状、尺寸大小、几何分布形态、分布点、增强(韧)体的体积分数、取向分布等均可按照设计要求做任意调整、随意组合，以满足实际材料微观组织结构的特征要求，提高了仿真的准确性，对复合材料微观组织结构的力学响应计算与失效分析起到至关重要的作用。

REFERENCES

[1] Ostoja-Starzewski M. Random field models of heterogeneous material[J]. Int J Solids, 1998, 35: 2429-2455.

[2] Moorthy S, Ghosh S. A voronoi cell finite element model for particle cracking in elastic-plastic composite materials[J]. Comput Methods Appl Mech Eng, 1998, 151: 377-400.

[3] Buryachenko V A. Multiparticle effective field and related methods in micromechanics of composite materials[J]. Appl Mech Rev, 2001, 54: 1-47.

[4] Kumar S. Computer simulation of 3D material microstructures and its application in the determination of mechanical behavior of polycrystalline materials and engineering structures[D]. Pennsylvania: The Pennsylvania State University, 1992: 26-34.

[5] Kumar S, Kurtz S K, Agarwala V K. Micro-stress distribution within polycrystalline aggregate[J]. Acta Mech, 1996, 114: 203-216.

[6] Aurenhammer F. Power diagrams: Properties, algorithms and applications[J]. SIAM Journal on Computing, 1987, 16(1): 78-96.

[7] Lautensack C. Fitting three-dimensional Laguerre tessellations to foam structures[J]. Journal of Applied Statistics, 2008, 35(9): 985-995.

[8] Fan Z, Wu Y, Zhao X, Lu Y. Simulation of polycrystalline structure with Voronoi diagram in Laguerre geometry based on random closed packing of spheres[J]. Computational Materials Science, 2004, 29: 301-308.

[9] Coster M, Arnould X, CHERMANT J L, EIMOATAZ A, CHARTIER T. A microstructural model by space tessellation for a sintered ceramic: Cerine[J]. Image Anal Stereol, 2005, 24: 105-116.

[10] Li M, Ghosh S, Richmond O, Weiland H, Rouns T N. Three-dimensional characterization and modeling of particle reinforced metal matrix composites: Part I. Quantitative description of microstructural morphology[J]. Materials Science and Engineering A, 1999, 265: 153-173.

[11] LI M, Ghosh S, Richmond O, Weiland H, Rouns T N. Three dimensional characterization and modeling of particle reinforced metal matrix composites: part Ⅱ. Damage characterization[J]. Materials Science and Engineering A, 1999, 266: 221-240.

[12] LI X D. Visualized simulation and modularized architecture of micro structure for composite materials[J]. Composite Interfaces, 2005, 12(3): 291-309.

[13] 李旭东. 复合材料微观组织结构的计算机可视化表征[C]//2004年材料科学与工程新进展论文集. 北京: 冶金工业出版社, 2004: 1103-1111.

LI Xu-dong. Computational imitation of microstructures for composite materials[C]//Proceedings of the New Progress on Material Science and Engineering. Beijing: Metallurgical Industry Press, 2004: 1103-1111.

[14] 任淮辉, 李旭东. 三维材料微结构设计与数值模拟[J]. 物理学报, 2009, 58(6): 4041-4052.

REN Huai-hui, LI Xu-dong. 3D material microstructure design and numerical simulation[J]. Acta Phys Sin, 2009, 58(6): 4041-4052.

[15] 李俊琛, 李旭东, 盛 捷. 异质体材料三维微观组织结构的可视化仿真[J]. 吉林大学学报: 工学版, 2010, 40(1): 92-97.

LI Jun-chen, LI Xu-dong, SHENG Jie. Visualized simulation of heterogeneous 3D material microstructure[J]. Journal of Jilin University: Engineering and Technology Edition, 2010, 40(1): 92-97.

[16] 毛卫民. 金属材料的晶体学织构与各向异性[M]. 北京: 科学出版社, 2002.

MAO Wei-min. Crystallographic texture and anisotropy of metals[M]. Beijing: Science Press, 2002.

[17] 彭 可, 易茂中, 刘 勋, 冉丽萍, 葛毅成, 杨 琳. SiC/MoSi₂纳米复合材料的显微结构与力学性能[J]. 中国有色金属学报, 2009, 19(12): 2155-2161.

PENG Ke, YI Mao-zhong, LIU Xun, RAN Li-ping, GE Yi-cheng, YANG Lin. Microstructure and mechanical properties of SiC/MoSi₂ nanocomposites[J]. The Chinese Journal of Nonferrous Metals, 2009, 19(12): 2155-2161.

(编辑  李艳红)

基金项目：国家自然科学基金资助项目(50571042)

收稿日期：2012-07-21；修订日期：2013-10-25

通信作者：李旭东，教授，博士；电话：13099102150；E-mail：lixd@luit.cn