J. Cent. South Univ. Technol. (2011) 18: 1609-1613
DOI: 10.1007/s11771-011-0879-z
Inverse synthetic aperture radar imaging based on sparse signal processing
ZOU Fei(邹飞)1, LI Xiang(黎湘)1, Roberto Togneri2
1. Institute of Space Electronic Technology, National University of Defense Technology, Changsha 410073, China;
2. School of Electrical, Electronic and Computer Engineering, The University of Western Australia, Terth, Australia
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract: Based on the measurement model of inverse synthetic aperture radar (ISAR) within a small aspect sector, an imaging method was presented with the application of sparse signal processing. This method can form higher resolution inverse synthetic aperture radar images from compensating incomplete measured data, and improves the clarity of the images and makes the feature structure much more clear, which is helpful for target recognition. The simulation results indicate that this method can provide clear ISAR images with high contrast under complex motion case.
Key words: ISAR imaging; sparse component analysis; target recognition; high resolution target image
1 Introduction
This work deals with the problem of inverse synthetic aperture radar (ISAR) imaging of multi-scatter targets. High resolution target images can be obtained using the ISAR technique. A wide bandwidth waveform is transmitted to achieve fine range resolution. Coherently processing the echoes returned from the target at different aspect angles gives fine cross-range resolution [1-2]. In ISAR, the angular aperture under which the target is viewed by the radar is due to the motion of the target itself. In order to get well focused images the instantaneous radar-target distance, and therefore the target motion, must be exactly known [3]. Moreover, the orientation of the image projection plane (IPP) depends on the target motion, which means that the IPP is normal to the effective rotation rate vector (the rotation rate component normal to the line of sight (LOS)). High quality images can be obtained when the rotation axis is almost fixed during time aperture [4-5].
Ideally, if the target has only uniform rotational motion and the data are collected over a small angular aperture, a simple Fourier transform process would bring a set of range profiles collected over a given dwell time (i.e., the coherent processing interval) into a focused two-dimensional image. However, actual targets observed by operational radar rarely have such an ideal motion. Targets are often engaged in complicated maneuvers that combine translational and rotational motions. For long imaging time i.e., long coherent integration time or for fast maneuvering targets, simple
Fourier processing without compensation will lead to reverse image blurring in cross-range. Unless a good motion compensation algorithm is implemented, serious blurring may occur in the ISAR image formed by Fourier transform [6-7].
In the present work, an ISAR imaging method based on sparse signal processing was presented for complex motion target.
2 Signal model
As shown in Fig.1, O is the center point of the target, and P (coordinate xP, yP, zP) is one of the scatter points of the target, which is denoted as vector rP. The rotating vector of the target is ω. On the plane decided by vector ω and the line of sight (R, the unit vector of LOS), ω can be decomposed to ωR (parallel to R) and ωe (perpendicular to R). The scatter moving generated by vector ωR does not have radial component, so it cannot bring phase variation to the echoes. Contrastively, vector ωe produces radial moving to the scatter points, and generates Doppler changing consequently, so it can be used to obtain high resolution imaging. Therefore, ωe is denoted as effective rotating vector. The linear velocity of scatter P is ωe×rP, and its radial component is (ωe×rP)?R.
Considering the translational motion components of the target as vr, the Doppler frequency of scatter P can be written as [8]:
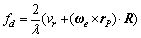(1)
where “?” and “?” denote the external product and inner product of two vectors, respectively, λ is the wavelength of the signal. As the imaging time is usually short, the projection image plane can approximately be considered invariant during this short period. So, the Doppler frequency of scatter point P can be further written as
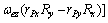(2)
where ωex, ωey and ωez denote the projection elements of vector ωe on three axes; rPx, rPy and rPz denote the projection elements of vector rP (the position vector of scatter point P) on three axes; Rx, Ry and Rz denote the projection elements of unit vector R on three axes. When the target motion is complex, ωex, ωey and ωez are usually not constants and change with time. As the imaging time is short, high order terms can be ignored, so, ωex, ωey and ωez can approximately be expressed as
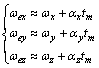(3)
where tm denotes the azimuth slow time, ωex, ωey and ωez are constant term coefficients, αx, αy and αz are one degree term coefficients. Substituting Eq.(3) in Eq.(2), then the Doppler frequency expansion of complex motion target can be obtained:
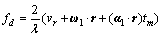(4)
where
; 
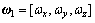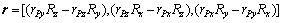
So, the operating range of target scatter point P can be obtained based on Eq.(4):
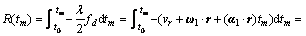
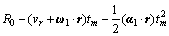(5)
where t0 denotes the initial time of azimuth imaging and R0 denotes the initial range of radar and target center. Due to the complex target motion, the instantaneous range of radar and the target scatter points embodies a characteristic of quadratic term, which is expressed as a characteristic of frequency modulation term when converting to azimuth phase. This frequency modulation will seriously affect the azimuth Doppler imaging. Assume the complex envelope of radar transmit signal as
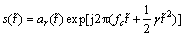(6)
where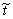 
denotes the range fast time, fc denotes the carrier-frequency of transmit signal, γ denotes the frequency modulation rate of transmit signal. The fundamental frequency echo can be written as
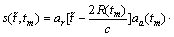
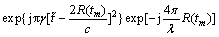(7)
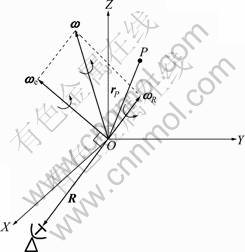
Fig.1 Imaging model of 3-D rotation traget
After the match filtering of range direction, Eq.(7) turns into
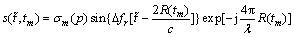(8)
From Eq.(5) and Eq.(8), it can be seen that after range compression, the complex target motion will produce serious envelope migration and azimuth phase quadratic term. The envelope migration can be well corrected by range alignment and keystone method, which has been detailedly discussed in relevant literatures. The presented method of this work concentrates on azimuth processing to reduce the effect of azimuth phase quadratic term, and to achieve high resolution ISAR imaging.
3 Sparse signal processing
Inverse synthetic aperture radar is usually used in detection and recognition of artificial metal targets. In high frequency region, this kind of targets can be described by a few scatter points, and these scatter points are also the driving source of echo signals. The sparse component analysis technology uses this structural prior information of radar target to obtain the essential driving source of echo signal, thus generates higher resolution ISAR image [9-11].
After rang compression and envelope alignment, azimuth ISAR processing of echo signal is mainly based on the exponential term in Eq.(8). It can be seen from Eq.(5) that the azimuth phase represented by exponential term in Eq.(8) contains target translational error vr. When vr is a constant, it mainly affects the position of ISAR image. When vr changes with time, it will bring frequency modulated term on azimuth phase which affects the quality of azimuth imaging and needs to be compensated. The multiple dominant scatters synthesis method can well correct the phase error caused by target translation and remove the effects of translational component vr on azimuth phase. As the azimuth imaging is implemented on different range cells, the characteristic of azimuth echoes in one range cell is considered. After phase translational error compensation, the azimuth signal of one range cell in Eq.(8) can be shortly written as
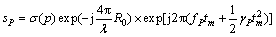(9)
where
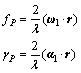
The first exponential term of Eq.(9) is an invariable term and has no effect on imaging. The second exponential term is used for azimuth imaging. For convenient analyzing, only the second exponential term is reserved, thus, Eq.(9) can be shortly written as
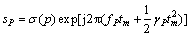(10)
To have a good understanding on how to apply sparse signal representation technique, it is useful to describe the imaging problem in a concise form. Suppose there are N scatters in a range cell. During the coherent processing, the total rotating angle is sampled into M points, i.e., m=0, 1, …, M-1. When M
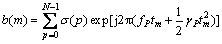(11)
Let
(12)
Equation (11) can be expressed in a matrix equation form:
Ax=b (13)
where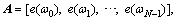 
is the M×N (M
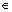CN to a limited radar data set b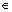CM. Here, the columns of A are generated by selecting the values of ω within the range (-π, π) to sample the frequency axis with the desired density. And then, the ISAR imaging problem now is transformed into estimating x from the observed radar data b.
The sparse signal representation problem is given by
Ax=b (14)
where A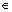CM×N, is a matrix operator from an unknown signal x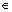CN to a limited data set b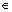CM, whose columns represent a possibly over-complete basis (M
This is equivalent to representing with a minimal number of the basis vectors. That is to solve the following problem:
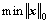subject to Ax=b
where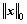 
is simply the number of non-zeros in x.
Unfortunately, finding the solution is in general NP hard. Considering replacing the l0-norm by the l1-norm, we get the following minimization problem:
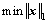subject to Ax=b
where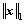 
is the l1-norm of x. That is basis pursuit
algorithm, which is a convex optimization problem and can be cast as a linear programming problem.
According to general separable sparse measurement
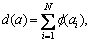the penalty function method and the
technology of gradient decomposition can be used to get the iterative algorithm of sparse solution in Eq.(14) [12-13]:
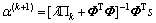(15)
where
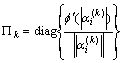(k=0, 1, 2, …)
Πk denotes iterative steps, and λ is the parameter of penalty function.
4 Simulation and discussion
ISAR imaging simulation: assume one c-band radar and one x-band radar observe the same target. The center frequency of c-band radar is f0=5 800 MHz, and the center frequency of x-band radar is f0=9 060 MHz. The two radars have the same sampling rate and bandwidth, which are 5 MHz and 400 MHz, respectively. The scatter points distribution of the space target is shown in Fig.2. The relative translational velocity of radar and target is 5 000 m/s, and the relative rotation angular velocity is 4 (°)/s.
The imaging results by direct 2-D FFT are shown in Fig.3. Figure 3(a) is the imaging of x-band and Figure 3(b) is the imaging of c-band. It can be seen that the images are blurring in Fig.3, and have different offset in 2-D direction. Figures 4(a) and 4(b) are respectively the imaging results of x-band and c-band after translational term compensation, fast-time quadratic term compensation and Doppler compensation.
It can be seen that the two bands signals have the same image position after velocity and Doppler compensation, and the quality of range imaging is improved, but the Doppler dimension of the cross range is visibly different. The imaging result of x-band is wider than that of c-band. The keystone transform is used to unify the scale, and the results are shown in Fig.5.
From Fig.5, it can be seen that the two wave bands data have the same cross range sampling scale, so the cross range image dimension of the two wave bands are also accordant. After range interpolation, the equivalent ultra waveband ISAR images are gained. In this simulation, the theoretic waveband can reach 4 700 MHz by frequency interpolation and band extrapolation.
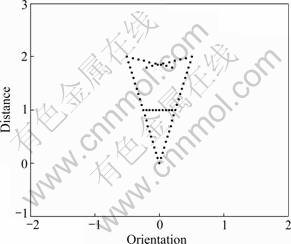
Fig.2 Shape diagram of space target
For convenient performance comparison, Fig.6(a) shows the imaging result of the whole band (4 700 MHz), and Fig.6(b) shows the result of imaging method presented in this work.
It can be seen from Fig.6(b) that the imaging result of the present work has higher resolution than the two sub-bands images shown in Fig.5, close to the resolution of the whole band shown in Fig.6(a). The imaging method in the present work is effective for increasing the ISAR image resolution.
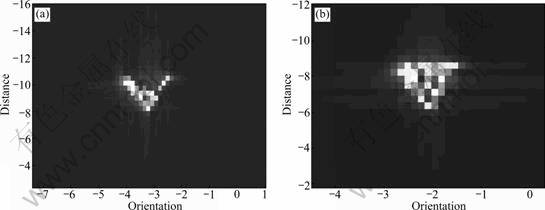
Fig.3 Imaging results of two wave bands without velocity compensation: (a) Imaging result of x-band; (b) Imaging result of c-band
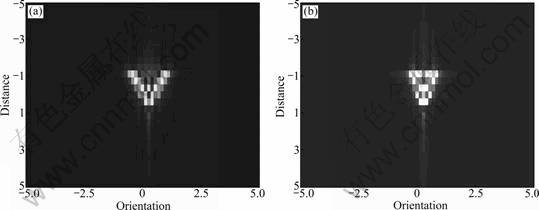
Fig.4 Imaging results of two wave bands after velocity compensation: (a) Imaging result of x-band; (b) Imaging result of c-band
Fig.5 Imaging results of two wave bands after cross range scale transform: (a) Imaging result of x-band; (b) Imaging result of c-band
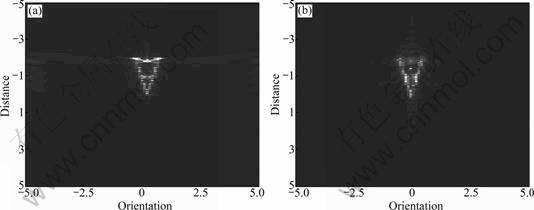
Fig.6 Imaging comparison: (a) Imaging result of the whole band; (b) Imaging result of sparse signal processing
5 Conclusions
A novel sparse signal processing algorithm for ISAR imaging of complex motion targets was presented. Imaging results of experimental data show that the proposed method is an effective and a promising imaging method for ISAR.
References
[1] DANIELS D J. Surface-penetrating radar [J]. Electron Commun Eng J, 1996, 8: 165-182.
[2] GRANDJEAN G, GOURRY J, BITRI A. Evaluation of GPR techniques for civil-engineering applications: Study on a test site [J]. J Appl Geophys, 2000, 45(3): 141-156.
[3] GADER P, MYSTKOWSKI M, ZHAO Y. Landmine detection with ground penetrating radar using hidden Markov models [J]. IEEE Trans Geosci Remote Sens, 2001, 39: 1231-1244.
[4] FENG X, SATO M. Pre-stack migration applied to GPR for landmine detection [J]. Inverse Prob, 2004, 20: 99-115.
[5] GROENENBOOM J, YAROVOY A. Data processing and imaging in GPR system dedicated for landmine detection [J]. Subsurf Sens Technol Appl, 2002, 3(4): 387-402.
[6] SCIOTTI M, COLONE F, PASTINA D, BUCCIARELLI T. GPR for archaeological investigations: Real performance assessment for different surface and subsurface conditions [C]// Proceedings of IGARSS 03. 2003: 2266-2268.
[7] HUBBARD S, CHEN J, WILLIAMS K, RUBIN Y, PETERSON J. Environmental and agricultural applications of GPR [C]// Proceeding of the 3rd Int Workshop on Adv Ground Penetrating Radar. Delft, Netherlands, 2005: 45-49.
[8] DANIELS D. Ground penetrating radar, 2nd ed [M]. London, U.K.: The Inst Elect Eng (IEE), 2004.
[9] POGGI G, RAGOZINI A R P, VERDOLIVA L. Compression of SAR data through range focusing and variable-rate vector quantization [J]. IEEE Trans Geosci Remote Sens, 2000, 38(3): 1282-1289.
[10] QI Hai-ming, YU Wei-dong, CHEN Xi. Piecewise linear mapping algorithm for SAR raw data compression [J]. Science in China Series F: Information Sciences, 2008, 51: 2126-2134.
[11] ZHAO Y P, WAN F, LEI H. Compression on fractional saturation SAR raw data [J]. J Electr Inform Tech, 2004, 26(3): 489-494. (in Chinese)
[12] MAX J. Quantizing for minimum distortion [J]. IRE Trans Inform Theory, 1960: 7-12.
[13] LLOYD S. Least squares quantization in PCM [J]. IEEE Trans Inform Theory, 1982, 28(2): 129-137.
(Edited by HE Yun-bin)
Foundation item: Project supported by the National Natural Science Foundation of China
Received date: 2011-07-01; Accepted date: 2011-07-29
Corresponding author: LI Xiang, Professor, PhD; Tel: +86-731-84575716; E-mail: lixiang@nudt.edu.cn
