DOI: 10.11817/j.issn.1672-7207.2016.11.044
高海拔地区铁路隧道施工期有害气体运移特性
曹正卯1, 2,杨其新1,郭春1
(1. 西南交通大学 土木工程学院 交通隧道工程教育部重点实验室,四川 成都,610031;
2. 招商局重庆交通科研设计院有限公司,重庆,400067)
摘要:依托西格二线新关角隧道工程,基于关角隧道地区实测气象资料,利用流体计算软件FLUENT,采用三维k-ε湍流非稳态模型,对不同海拔高度地区铁路隧道内施工期有害气体运移特性和质量浓度分布规律进行数值模拟计算分析。研究结果表明:考虑湿度与不考虑湿度对空气密度计算结果影响误差为0.3 %左右,可以忽略不计;有害气体在隧道内向洞口运移的动态过程中,最高质量浓度逐渐降低、体积逐渐增大,在隧道内呈U型分布;随着海拔高度增加,由于环境气压的影响,同一测点有害气体质量浓度随海拔高度以指数形式增大,CO增加倍数可按K=eh/104进行计算,且达到容许质量浓度的时间增加。
关键词:高海拔;铁路隧道;施工通风;有害气体;数值模拟;运移特性
中图分类号:U25 文献标志码:A 文章编号:1672-7207(2016)11-3948-10
Migration characteristics of poisonous gas during construction stage in railway tunnels at high altitude areas
CAO Zhengmao1, 2, YANG Qixin1, GUO Chun1
(1. Key Laboratory of Transportation Tunnel Engineering, Ministry of Education,
School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China;
2. China Merchants Chongqing Communications Research and Design Institute Co. Ltd., Chongqing 400067, China)
Abstract: According to the measured meteorological data of new Guanjiao tunnel project located on Xining—Golmud railway, the migration characteristics and the regularity variation at different altitudes of poisonous gas concentration in railway tunnels during construction stage were simulated and analyzed with FLUENT through the three-dimensional k-ε unsteady turbulent model. The results indicate that the influence of air humidity on the deviation of air density calculation results is about 0.3%, which is negligible. The peak concentration of poisonous gas decreases and the volume increases gradually in the dynamic processes of migration to the tunnel entrance, which is in U-shaped distribution in the tunnel. For the impact of environmental atmospheric pressure with the altitude increasing, the concentration of poisonous gas increases exponentially at the same measuring point. The increase in multiples of CO can be calculated by K=eh/104, and more time is required to reach the allowable concentration.
Key words: high altitude; railway tunnels; construction ventilation; poisonous gas; numerical simulation; migration characteristics
目前,长大隧道施工期间通风往往成为影响隧道施工进度、施工安全的一项重要因素,与作业人员的健康密切相关,通常按照经验或根据规范进行通风方案的制定[1-2]。对于隧道通风问题的研究,国外起步较早,日本、挪威、瑞士、奥地利等国家针对隧道通风进行了大量研究,但主要集中在对隧道运营期间通风和地下矿井通风的研究,对于隧道施工期的通风研究相对较少[3-6]。我国隧道工程建设起步较晚,但随着隧道工程事业的蓬勃发展,我国已积累了丰富的工程经验,并取得了大量的科研成果。对于隧道施工通风的研究主要集中在通风流场特性、风流组织、施工通风技术以及施工通风方案优化等方面[7-9]。对于爆破后隧道内污染物运移的研究,王晓玲等[10]建立了压入式紊流高雷诺数k-ε的数学模型,对隧道内风流组织和CO浓度分布规律进行了非稳态数值模拟;张静等[11]利用三维非稳态欧拉两相流模型对隧道掌子面爆破后的通风过程以及粉尘扩散进行了数值模拟;朱红青等[12]通过对大断面压入式通风风管布设的不同形式进行了数值模拟,比较通风20 min后CO的稀释效果和通风死区比例,得出风管布设的最佳高度;邓祥辉等[13]对施工阶段隧道内的CO扩散规律以及工作人员进洞安全时间进行了数值模拟研究;危宁等[14]对隧道施工期间污染物扩散进行理论分析,得出洞内不同通风量情况下的通风效果;刘钊春等[15]利用有限元分析软件ADINA对压入式通风情况下涡流区对有害气体的影响进行了数值模拟研究。从国内外的研究成果可以看出,对于施工期间有害气体的研究基本上针对平原地区的隧道,而对于高海拔地区隧道内污染物运移规律的研究极少。在高海拔地区,由于海拔的增加,环境特点改变,如空气密度减小、气压及温度降低,相对于低海拔地区的施工通风显得更加重要。本文作者依托西格二线新关角隧道实际情况,针对不同海拔高度,考虑大气压力、环境温度、空气密度等影响因素对施工通风期间有害气体运移特性进行研究,为今后高海拔地区隧道施工通风理论以及通风方案的设计提供理论依据和指导。
1 关角隧道工程概况
西格二线新关角隧道位于海拔3 300 m以上的青藏铁路西宁至格尔木段,全长32.645 km,是迄今为止世界上罕见的高海拔地区特长铁路隧道。新关角隧道为线间距40 m双洞单线隧道,进口段为8‰的上坡,在岭脊以后为9.5‰的连续下坡。隧道通过地区属青藏高原亚寒带半干旱气候区,存在如高寒、低气压、风沙大、干旱等诸多不同于一般隧道地区的特点,隧道所在地区环境大气压力仅为海平面处大气压的60%~70%,空气中氧气含量仅为13%~16.5%。由于处于高原地区存在大气压力低、空气密度小、低温等因素影响,施工期间隧道内有害气体扩散相对于平原地区具有特殊性[16]。
2 高海拔地区环境特点
2.1 海拔高度对大气压力的影响
环境大气压在数值上为测试位置所在地区以上整个空气柱的重力,在理想情况下,环境大气压力与海拔高度具有对应关系,随着海拔高度的不断增加,大气压力逐渐减小,两者具有非线性关系。海拔11 km以下地区大气压力通常按下式计算:
 (1)
(1)
式中:ph为海拔高h处的大气压力,Pa;h为海拔高度,m。
大气压力与海拔高度的关系如图1所示。

图1 不同海拔高度条件下大气压力
Fig. 1 Atmospheric pressure changing regularities at different altitudes
2.2 海拔高度对温度的影响
环境温度不仅与地理纬度变化的影响有关,而且受海拔高度增加的影响逐渐降低。
 (2)
(2)
式中:th为海拔高度h处的温度,℃;tA为相邻气象站的温度,℃;gt为温度梯度,0.5~0.7 ℃/(100 m); 为海拔h处与相邻气象站高程差,m。
为海拔h处与相邻气象站高程差,m。
2.3 海拔高度对空气密度的影响
隧道内外空气的密度与隧道所处地区的大气压力、温度以及湿度有关。
 (3)
(3)
式中:ρ为空气密度,kg/m3;psat为饱和水蒸气压力,Pa; 为相对湿度,%;P为环境大气压,Pa;t为环境温度,℃。
为相对湿度,%;P为环境大气压,Pa;t为环境温度,℃。
为得到湿度对空气密度的影响,对关角隧道气象站所实测的数据进行分析,表1所示为根据关角隧道地区天峻气象站(N37°18′E99°02′,3 417.1 m)实测数据进行空气密度计算的部分结果。
从考虑湿度与不考虑湿度的计算可以看出:两者计算结果误差平均为0.3%左右,误差小于0.5%,在计算中可以认为空气湿度对空气密度的影响极小。空气密度可按下式计算:
 (4)
(4)
3 数学模型
隧道内有害气体浓度随通风过程的进行随时间变化,其稀释及扩散的过程为非稳态过程,本文采用三维非稳态组分输运模型进行求解,湍流模型采用标准k-ε双方程模型,总体模型包括质量守恒方程、动量守恒方程、组分输运方程、能量耗散率方程以及湍动能方程[17]。
3.1 基本假设
1) 隧道施工通风情况下,风管出口风速较大,但其马赫数仍然小于0.3,可不考虑其压缩性,通常认为隧道内风流运动处于紊流流动状态,因此,可以假定隧道内空气域流场为三维黏性的不可压缩湍流场;
2) 假定壁面绝热,忽略由黏性力做功引起的耗散热;
3) 忽略洞内其他设备及障碍物对流场的扰动,对洞内交通风及自然阻力的影响忽略不计。
表1 湿度对空气密度计算结果的影响
Table 1 Influence of humidity on air density calculation result

3.2 控制方程
1) 连续性方程:
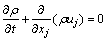 (5)
(5)
2) 动量方程:
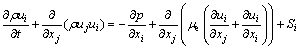 (6)
(6)
其中:
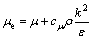 (7)
(7)
3) 组分输运方程:
 (8)
(8)
4) 湍动能k方程:
 (9)
(9)
5) 湍动能耗散率 方程:
方程:
 (10)
(10)
其中:
 (11)
(11)
式中:uj为xj方向上空气速度分量,m/s;μ为层流动力黏性系数,Pa·s;μT为紊流动力黏性系数,Pa·s;Si为动量源项;μe为等效动力黏性系数,Pa·s;Ym为质量分率;k为紊流动能,m2/s2;ε为紊流动能耗散率,m2/s3;Gk为紊流脉动动能产生项;c1,c2,cμ,σk,σε和 为经验常数,取值如下[18-19]:
为经验常数,取值如下[18-19]: =0.09,c1=1.44,c2=1.92,
=0.09,c1=1.44,c2=1.92, =1.0,
=1.0, =1.33,
=1.33, =1.3。
=1.3。
4 模型建立与参数设定
4.1 模型建立及网格划分
利用目前广泛使用的大型计算流体动力学(CFD)有限元计算软件FLUENT对不同工况进行三维数值模拟计算。前期利用专业CFD前处理建模软件GAMBIT根据隧道基本参数进行横断面1:1计算模型建立,隧道长度取1 000 m,根据以往对风管布设形式的研究成果[20],对风管布设位置如图2所示,风管出风口距掌子面距离为20 m,
模型相关参数设置见表2。

图2 隧道内风管布设位置简图
Fig. 2 Sketch of wind duct position in tunnel
表2 计算模型参数
Table 2 Defining calculation model parameters

风管出口处风流速度和压力梯度极大,对其附近网格进行适当加密。根据非稳态计算经验,并考虑到模拟计算的计算规模、稳定性及收敛性,在进行模型网格划分时采用规则的六面体网格,模型网格数总计约为40万个,计算模型网格划分如图3所示。

图3 模型网格划分
Fig. 3 Grid of model
4.2 边界条件
根据分析,结合实际情况,对边界条件设定如下[21]。
1) 入口边界条件:隧道内风管末端出风口定义为速度入口边界条件(velocity-inlet),速度设定为v= 20 m/s;紊流动能为
 (12)
(12)
紊流动能耗散率为
 (13)
(13)
式中:kin为入口边界紊流动能,m2/s2;εin为入口边界紊流动能耗散率,m2/s3;Uin,Cμ和Lm为试验常数;R为通风管水力半径。其中, =0.09,
=0.09, =0.005,Lm=0.03R。
=0.005,Lm=0.03R。
2) 出口边界条件:隧道出口设定为压力出口边界条件(pressure-outlet),根据不同海拔高度工况设定环境大气压力。
3) 壁面边界条件:模型采用无滑移固壁边界条件(wall),并且考虑粗糙度影响的壁面函数[5]。
 (14)
(14)
式中:Up为近壁面网格点的速度,m/s;U*为摩阻速度,m/s;yp为网格点到壁面的距离,m;κ为卡门常数,取κ=0.42;E为表征粗糙率的参数(E=9.8);cks为壁面粗糙度常数;ks+为壁面平均粗糙高度,m。根据“铁路隧道运营通风设计规范”,壁面粗糙度常数取0.6,壁面平均粗糙高度取0.08 m。
4.3 初始条件
隧道爆破产生的有害气体(主要为CO)初始质量浓度按下式计算:
 (15)
(15)
式中:c为CO初始质量浓度,kg/m3; 为炸药质量,kg;
为炸药质量,kg; 为1 kg炸药爆破产生的有害气体质量,kg;L为炮烟抛掷带长度,m,按15+mG/5计算;S为隧道开挖面积,m2。
为1 kg炸药爆破产生的有害气体质量,kg;L为炮烟抛掷带长度,m,按15+mG/5计算;S为隧道开挖面积,m2。
隧道内其余部分产生的有害气体忽略不计,计算得CO初始质量浓度为3 082 mg/m3。
4.4 工况设置
根据不同海拔高度对计算工况进行设置,具体工况设置情况如表3所示。
5 计算结果及分析
5.1 速度流场特性
由于风管出风口处风流的射流作用,使得掌子面附近风流分布情况较复杂,取隧道纵断面x=3.5 m处和水平剖面y=6.0 m处流场进行分析,速度矢量如图4所示。
表3 计算工况参数
Table 3 Calculation parameters of working conditions


图4 掌子面附近风流速度矢量图
Fig. 4 Velocity vector profiles around heading face
风流自风管口射流运动过程中,射流体不断吸卷周围的空气,随着射流距离的增加,射流的范围增大,但在隧道内受到有限空间以及空气回流的影响,使得射流的发展受到限制,射流体向外析出空气,射流体的吸卷与析出有较明显的分界面,此处出现了明显的涡流。从图4可以看出:射流过程中分为几个明显的区域,即附壁射流区、冲击射流附壁区、回流区、涡流区、稳定区[7]。风管中的风流自风管出口射向掌子面,由于有限空间的限制,风流受到阻碍,由隧道另一侧回流,一部分回流的空气在到达风管出风口附近时,受射流体的吸卷作用又流向掌子面,形成1个风流旋涡,即涡流区。由于涡流区的存在,对掌子面附近的有害气体排出有不利影响,部分有害气体在涡流区循环流动,需较长的时间稀释和排出。
图5所示为隧道内不同高度处沿程风速分布。

图5 隧道内风速沿程分布
Fig. 5 Wind velocity distribution along tunnel
从图5可以看出:隧道内1 m高度处及10 m高度处风速在距掌子面50 m处急剧降低,在距掌子面150 m之后风速基本趋于平稳,隧道中部风速最大,风速稳定在0.72 m/s左右;隧道顶部风速最小,稳定段风速为0.46 m/s左右。距离掌子面越近,洞内风速波动越大,距掌子面超过150 m以后,风速基本趋于稳定,风流处于稳定区。在风流稳定区内,风速分布情况为隧道中部风速大,距隧道壁越近的区域风速越小,这与流体力学的基本理论是完全一致的。
5.2 CO运移特性
隧道内CO质量浓度分布特性与隧道内流场分布、压力场分布等密切相关。以工况一计算结果对CO运移特性进行分析。图6所示为隧道爆破后通风6 min内掌子面附近隧道中心线纵向剖面x=0 m处CO质量浓度分布云图。在进行通风1 min后,由于风流的稀释和压力作用,将洞内CO向外排出。从图6可以看到:由于涡流区的存在,涡流区内CO质量浓度明显偏高。随着通风时间的增加,CO不断被稀释,并朝隧道洞口移动,隧道内CO最高质量浓度不断减小,含有CO的空气体积不断膨胀。隧道中部CO排出速度较快,靠近隧道壁附近的CO排出速度较慢,在隧道内呈U形分布。

图6 x=0 m平面CO质量浓度分布
Fig.6 CO mass concentration distribution at section of x=0 m
图7所示为隧道内呼吸带高度CO质量浓度分布。以隧道中心纵断面人体平均呼吸高度y=1.6 m处CO质量浓度分布进行研究,考察通风时间1,5,10,20和30 min时隧道内CO质量浓度分布情况。从图7可以看出:通风不同时刻的CO质量浓度分布有以下规律。通风1 min时,CO质量浓度最大值处于回流区范围;随着时间的推移,监测点CO质量浓度最大值逐渐减小,充斥CO的空气团由于风流的作用不断向隧道洞口移动;通风时间的增加使得CO气团体积不断膨胀,其跨度不断变大。

图7 隧道内呼吸带高度CO质量浓度分布
Fig. 7 CO mass concentration distribution at breathing height in tunnel
图8所示为t=5 min和t=10 min时CO空气团所在区段隧道横断面的CO质量浓度分布云图。由图8可以看出:开始进行通风后,t=10 min时隧道内的CO质量浓度峰值较t=5 min时CO质量浓度峰值低,CO气团分布跨度较t=5 min时CO气团分布跨度长。CO气团区域隧道中部与隧道壁附近CO质量浓度分布有明显的差异。图9所示为爆破通风10 min时隧道内CO质量浓度分布情况。
从图9可以看出:由于相同条件下CO密度比空气稍轻,观察CO空气团运移较稳定的t=10 min时隧道中心纵断面监测点CO质量浓度分布,人体呼吸高度y=1.6 m处CO峰值较隧道中部(y=5 m)和隧道顶部(y=10 m)处低,隧道顶部(y=10 m)处CO质量浓度峰值最大。

图8 隧道横断面CO质量浓度分布
Fig. 8 CO mass concentration distribution at cross section in tunnel

图9 t=10 min时隧道内CO质量浓度分布
Fig.9 CO mass concentration distribution at t=10 min in tunnel
5.3 海拔高度对CO质量浓度分布的影响
由于通风初期CO气团距掌子面较近,受回流区及涡流区的影响较大,取t=10 min时CO运移较稳定的阶段对不同海拔高度情况下CO在隧道内的分布规律进行研究。本文仅讨论隧道中心纵断面人体呼吸高度y=1.6 m处CO质量浓度分布。
由于海拔高度的增加,各种环境因素(大气压力、空气密度、环境温度等)变化综合作用引起隧道内CO质量浓度分布的差异,其中大气压力的变化为最主要的因素。洞内静压分布随海拔高度的不同而变化,而静压在稀释和排出有害气体方面起着关键性的作用。
图10所示为通风后,t=10 min时隧道内部分测点在不同工况下的CO质量浓度变化。从图10可以看出:隧道内同一测点在其他条件不变的情况下,当海拔高度升高时,CO质量浓度有所升高。
为探明CO质量浓度随海拔高度升高的增加程度,在CO气团分布区域从z=200 m 至z=400 m每10 m取一测点计算CO质量浓度相对于海拔0 m时的增加倍数,计算结果如表4所示。
观察表4中z方向各测点变化,海拔高度较低时,CO质量浓度增加较少,随着海拔高度增加,CO质量浓度增加幅度增大,两者呈非线性增长关系。对不同测点CO质量浓度增加倍数取平均值,得到如图11所示关系曲线。
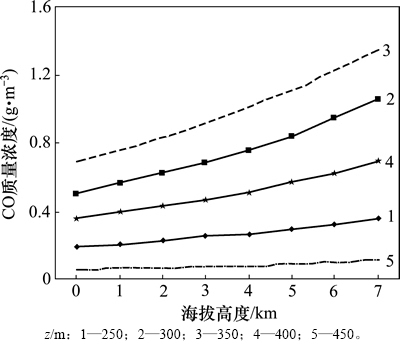
图10 不同海拔高度条件下CO质量浓度变化
Fig. 10 CO mass concentration variations along with different altitudes
表4 不同海拔高度条件下CO质量浓度增加倍数
Table 4 CO mass concentration increasing regularities at different altitudes

图11中曲线符合指数增长规律,定义系数K为高海拔地区CO质量浓度修正系数。经拟合得任意海拔高度h处CO质量浓度相对于海拔0 m处增加倍数为
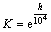 (16)
(16)
式中:K为CO质量浓度修正系数。

图11 不同海拔高度CO质量浓度变化
Fig. 11 CO mass concentration variations along with different altitudes
以隧道内人体平均呼吸高度y=1.6 m处距掌子面100和300 m处CO质量浓度达到规范规定的浓度限值所需时间,此处暂不考虑高海拔地区规范限值的变化,以规范中容许质量浓度和工作质量浓度作为判定标准。计算结果见表5。
由计算结果可以看出:海拔高度为0 m时,距掌子面100 m处CO质量浓度达到规范规定的容许质量浓度所需时间为8.32 min;随着海拔高度的增加,距掌子面100 m处CO质量浓度达到容许质量浓度的时间有所增加;在海拔7 000 m情况下需9.43 min,由于本次计算中边界条件设定风管出口风速为20 m/s,隧道内稳定段平均风速在0.5 m/s左右,测点在不同工况下达到容许质量浓度的时间差异不明显,若施工过程中洞内风速较小,则在不同海拔高度地区,洞内CO质量浓度达到容许质量浓度的时间差异较大。因此,建议在高海拔隧道施工时,为了保证施工作业人员的身体健康和施工环境安全,爆破后工作人员进入洞内的规定时间应适当延长。
表5 y=1.6 m处CO质量浓度达到容许质量浓度所需时间
Table 5 Time required to meet standards of allowable mass concentration at y=1.6 m

6 结论
1) 湿度对高海拔地区空气密度的计算结果影响误差为0.3 %左右,即湿度对空气密度的影响可以忽略不计,高海拔地区空气密度可按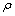 =0.003 484 p/t进行计算。
=0.003 484 p/t进行计算。
2) 隧道爆破后通风过程中,掌子面附近风流场涡流区的存在,使得此处CO排出需较长时间。
3) 随着距掌子面距离的增加,风流逐渐稳定,由于风流的稀释和推动作用,CO气团在向洞口运移的过程中,隧道内CO最高质量浓度逐渐减小,CO气团体积逐渐增大并整体向洞口运动。隧道中部的CO排出速度较快,靠近隧道壁的CO排出速度较慢,整个CO气团在隧道内排出过程中呈现U型分布。
4) 随着海拔高度的增加,环境条件的改变使得隧道内CO质量浓度升高,海拔高度的增加与CO质量浓度分布大致呈指数分布,CO增加倍数可按K=eh/104进行计算。
5) 随着海拔高度的增加,隧道内同一位置CO质量浓度达到容许质量浓度的时间有所增加,建议在高海拔地区施工期间适当延长通风时间,以保护隧道内施工作业人员身体健康和施工安全。
参考文献:
[1] JTG F60—2009, 公路隧道施工技术规范[S].
JTG F60—2009, Technical specification for construction of highway tunnel[S].
[2] TB 10204—2002, 铁路隧道施工规范[S].
TB 10204—2002, Code for construction on tunnel of railway[S].
[3] HARGREAVES D M, LOWNDES I S. The computational modeling of the ventilation flows within a rapid development drivage[J]. Tunnelling and Underground Space Technology, 2007, 22(2): 150-160.
[4] KURNIA J K, SASMITO A P, MUJUMDAR A S. Simulation of a novel intermittent ventilation system for underground mines[J]. Tunnelling and Underground Space Technology, 2014, 29(3): 206-215.
[5]  M, et al. Auxiliary ventilation in mining roadways driven with roadheaders: Validated CFD modelling of dust behaviour[J]. Tunnelling and Underground Space Technology, 2011, 26(1): 201-210.
M, et al. Auxiliary ventilation in mining roadways driven with roadheaders: Validated CFD modelling of dust behaviour[J]. Tunnelling and Underground Space Technology, 2011, 26(1): 201-210.
[6] NAKAYAMA. In-situ measurement and simulation by CFD of methane gas distribution at a heading faces[J]. Journal of the Mining and Materials Processing Institute of Japan, 1998, 114(11): 769-775.
[7] 王海桥, 施式亮, 刘荣华. 独头巷道附壁射流通风流场数值模拟研究[J]. 煤炭学报, 2004, 29(4): 425-428.
WANG Haiqiao, SHI Shiliang, LIU Ronghua. Numerical simulation study on ventilation flow field of wall-attached jet in heading face[J]. Journal of China Coal Society, 2004, 29(4): 425-428.
[8] 陈卫忠, 郭小红, 曹传林, 等. 公路分岔隧道循环风相互影响及其对策研究[J]. 岩石力学与工程学报, 2008, 27(6): 1137-1147.
CHEN Weizhong, GUO Xiaohong, CAO Chuanlin, et al. Research on interrelationship of exhaust air of highway forked tunnel and countermeasures[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(6): 1137-1147.
[9] 谢尊贤, 朱永全, 陈绍华, 等. 高原隧道长距离施工通风方法研究[J]. 现代隧道技术, 2011, 48(3): 112-116.
XIE Zunxian, ZHU Yongquan, CHEN Shaohua, et al. Research on ventilation for long distance construction of tunnels in plateau[J]. Modern Tunnelling Technology, 2011, 48(3): 112-116.
[10] 王晓玲, 陈红超, 刘雪朋. 引水隧洞独头掘进工作面风流组织与CO扩散的模拟[J]. 水利学报, 2008, 39(1): 121-127.
WANG Xiaoling, CHEN Hongchao, LIU Xuepeng. Simulation on ventilation air flow and CO diffusion in leading face of excavation in tunnel[J]. Journal of Hydraulic Engineering, 2008, 39(1): 121-127.
[11] 张静, 王晓玲, 陈红超. 引水隧洞独头掘进工作面风流和粉尘扩散的模拟[J]. 水力发电学报, 2008, 27(1): 111-117.
ZHANG Jing, WANG Xiaoling, CHEN Hongchao. Simulation on ventilation and dust diffusion on heading face of the diversion tunnel[J]. Journal of Hydroelectric Engineering, 2008, 27(1): 111-117.
[12] 朱红青, 朱帅虎, 贾国伟. 大断面掘进压入式风筒最佳高度的数值模拟[J]. 安全与环境学报, 2014, 14(1): 25-28.
ZHU Hongqing, ZHU Shuaihu, JIA Guowei. Numerical simulation for the optimal driving duct height in a large-scale cross-section of driving face[J]. Journal of Safety and Environment, 2014, 14(1): 25-28.
[13] 邓祥辉, 刘钊, 刘钊春. 两河口长隧道独头掘进压入式施工通风三维数值模拟[J]. 土木建筑与环境工程, 2014, 36(2): 35-41.
DENG Xianghui, LIU Zhao, LIU Zhaochun. 3D numerical simulation on forced construction ventilation of long single head tunnel of Lianghekou[J]. Journal of Civil, Architectural & Environmental Engineering, 2014, 36(2): 35-41.
[14] 危宁, 李力, 王春燕. 隧道施工通风中的有害气体浓度变化分析[J]. 三峡大学学报(自然科学版), 2006, 28(4): 324-327.
WEI Ning, LI Li, WANG Chunyan. Analysis of harmful gas concentration variation in tunneling ventilation[J]. Journal of China Three Gorges University (Natural Sciences), 2006, 28(4): 324-327.
[15] 刘钊春, 柴军瑞, 贾晓梅, 等. 压入式通风掘进面有害气体浓度扩散数值模拟[J]. 岩土力学, 2009, 12(30): 536-539.
LIU Zhaochun, CHAI Junrui, JIA Xiaomei, et al. Numerical simulation of concentration diffusion of harmful gas in heading face with forced ventilation[J]. Rock and Soil Mechanics, 2009, 12(30): 536-539.
[16] 曹正卯. 关角隧道运营通风防灾技术研究[D]. 成都: 西南交通大学土木工程学院, 2011: 11-12.
CAO Zhengmao. Study on the Technology of Operation Ventilation and Disaster Prevention of Guanjiao Railway Tunnel[D]. Chengdu: Southwest Jiaotong University. School of Civil Engineering, 2011: 11-12.
[17] 陶文铨. 数值传热学[M]. 2版. 西安: 西安交通大学出版社, 2001: 333-376.
TAO Wenquan. Numerical heat transfer[M]. 2nd ed. Xi’an: Xi’an Jiaotong University Press, 2001: 333-376.
[18] LANCE M, BATEILLE J. Turbulence in liquid and phase of a uniform bubbly air-water flow[J]. Journal of Fluid Mechanics, 1991, 22(2): 95-18.
[19] PATANKAR S V. Numerical heat transfer and fluid flow[M]. Washington: Hemisphere Publishing Corporation, 1980: 15-19.
[20] 方勇, 彭佩, 赵子成, 等. 风管出口位置对隧道施工通风效果影响的研究[J]. 地下空间与工程学报, 2014, 10(2): 468-473.
FANG Yong, PENG Pei, ZHAO Zicheng, et al. Numerical simulation of the effect of outlet position of air duct on the construction ventilation of the tunnel[J]. Chinese Journal of Underground Space and Engineering, 2014, 10(2): 468-473.
[21] 韩占中. FLUENT-流体工程仿真计算实例与分析[M]. 北京: 北京理工大学出版社, 2009: 37-45.
HAN Zhanzhong. FLUENT-fluid engineering simulation calculation example and analysis[M]. Beijing Institute of Technology Press, 2009: 37-45.
(编辑 陈爱华)
收稿日期:2016-01-12;修回日期:2016-03-25
基金项目(Foundation item):国家自然科学基金资助项目(51108384, 51478393);中央高校基本科研业务费专项基金资助项目(SWJTU11ZT33, 2682014CX062);教育部创新团队发展计划项目(IRT0955);中国铁路总公司科技研究开发计划项目(2013T001);铁道部科技研究开发计划项目(2008G030-C);重庆市基础与前沿研究计划项目(cstc2015jcyjBX0020) (Projects(51108384, 51478393) supported by the National Natural Science Foundation of China; Projects(SWJTU11ZT33, 2682014CX062) supported by the Fundamental Research Funds for the Central Universities; Project(IRT0955) supported by the Program for Innovative Research Team in University of Ministry of Education of China; Project(2013T001) supported by the Science and Technology Research and Development Program of China Railway Corporation; Project(2008G030-C) supported by the Science and Technology Research and Development Program of Ministry of Railways of China; Project(cstc2015jcyjBX0020) supported by the Foundation and Frontier Research Program of Chongqing)
通信作者:杨其新,教授,博士生导师,从事隧道及地下工程通风与防灾、隧道及地下工程防排水理论研究;E-mail:yangqixin113@163.com