GPU加速的在线K均值聚类粒子滤波跟踪算法

刘元元1，刘华平2，高蒙1，孙富春2，孟丽霞2

(1. 石家庄铁道大学 电气与电子工程学院，河北 石家庄，050043;

2. 清华大学 计算机科学与技术系，北京，100084)

摘要：针对目标的颜色空间特征，提出一种在粒子滤波框架下利用K均值聚类描述目标，并采用EMD距离度量2个聚类簇集之间的相似程度的跟踪算法。考虑到聚类算法的耗时，利用GPU将其并行化进行加速。实验结果表明，此法比基于颜色直方图的粒子滤波算法具有更好的跟踪效果，同时也显著提高了运算速度。

关键词：粒子滤波；K均值聚类；EMD距离；GPU

中图分类号：TP391          文献标志码：A         文章编号：1672-7207(2011)S1-0724-07

Particle filter tracking algorithm based on online K-means clustering and GPU accelerating

LIU Yuan-yuan1, LIU Hua-ping2, GAO Meng1, SUN Fu-chun2, MENG Li-xia2

(1. Institute of Electrical and Electronic Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;

2. Department of Computer Science and Technology, Tsinghua University, Beijing 100084, China)

Abstract: A new color space feature based particle filtering tracking algorithm is proposed. The algorithm uses K-means clustering for object description and EMD for the distance measure between two clustering. For the problem of the clustering algorithm’s time-consuming, GPU is used to parallel accelerating. The experimental results confirm that the proposed algorithm can yield good results as compared with a color histogram-based- method and the processing speed upgrades great are increased dramatically.

Key words: particle filter; K-means clustering; EMD distance; GPU

目标跟踪是计算机视觉领域的一个热点问题，广泛地应用于视频监控、目标识别、虚拟现实等领域。目前，目标跟踪的主要方法[1]包括：基于区域的跟踪、基于特征的跟踪、基于变形模板的跟踪以及基于模型的跟踪等。

颜色特征由于获取容易，描述简单等特点，广泛应用在目标跟踪中。同时，粒子滤波的引入很好的解决了非线性、非高斯观测下的滤波问题，在目标跟踪领域获得了成功的应用。粒子滤波方法是一种基于蒙特卡洛的最优贝叶斯滤波算法，不用函数的闭合形式来近似事件的后验分布，不受线性、高斯条件的限制。对跟踪各种复杂目标有着更加广泛的适用范围。

在目标跟踪过程中常常会遇到很多干扰因素，例如光照变化、遮挡等。其中光照变化是目标跟踪中经常遇到的现象。用Bhattacharyya系数度量目标模型和候选目标模型之间的相似性，其度量方法对光照变化敏感，当光照变化时跟踪不准确，甚至出现无法跟踪目标的情况[2]。Tao等提出的用两个分布间的EMD模型度量，使得跟踪性能有了很大的提高。EMD的计算是基于线性规划的，求解的复杂度很大，因此用较少的分布描述模型，是减少EMD计算的主要方法。

通常情况下，目标颜色的空间分布是非常紧凑的。因此，采用文献[2]的方法对目标的颜色空间进行剖分，使颜色直方图用数量较少的空间更能准确地表达目标的颜色概率密度。本文在此聚类的基础上，在粒子滤波的框架下完成对目标的跟踪。最后通过实验对本文算法的鲁棒性和实时性进行验证和分析。

在保证跟踪准确度的前提下，为了提高算法运算的速度，在GPU平台上对算法进行了并行优化，取得了较好的效果。

1  粒子滤波

粒子滤波的核心思想[3]是用一些离散随机采样点(粒子)来近似系统随机变量的概率密度函数 ，用样本的均值代替积分运算，从而获得状态最小方差估计。

假定一个系统的模型可以用状态转移方程和量测方程表示如下：

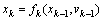
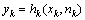
其中，xk服从一阶Markov过程，并且各个yk之间相互独立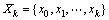，表示前k个时刻系统的状态向量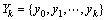，表示前k个时刻系统状态向量的观测，依据Bayesian滤波的观点，假定概率密度函数p(x0|y0)已知，滤波问题就是在给定观测数据序列Yk的基础上求解后验概率密度函数p(xk|Yk)。其中包括预测p(xk|Yk-1)和更新p(xk|Yk)两部分。

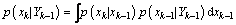    (1)

       (2)

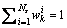粒子滤波算法就是采用一组带有权值的粒子表示后验概率密度函数p(xk|Yk)。通常粒子不能从状态的PDF中采样得到，而是从一个容易采样的已知分布的重要性分布函数中独立抽取得到。其中，是一组能够表示概率密度函数特征的随机抽样值；表示每个随机抽样值的权值，且满足。则k时刻的后验概率密度可以近似如下：

       (3)

在更新阶段，根据似然函数p(yk|xk)重新计算粒子的权值

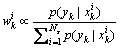                (4)

后验概率密度函数可以近似表示为：

                  (5)

2  似然函数

2.1  K均值聚类

在特征空间中对颜色特征矢量进行聚类处理，能够以较少的代价获得较为简洁的颜色分布的描述，称之为簇集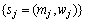，它由对颜色描述起主要作用的若干聚类及其相应的权值构成。相对于直方图这样数量固定的结构，簇集只是由原始特征分布中的主要聚类组成，大小灵活，弥补了直方图难以在表达能力和效率二者之间取得平衡的不足。

给定一个由N个像素组成的目标的参考图像，目标的模型表达为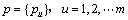，pu按照下式定义

         (6)

其中：xi是第i个像素的空间坐标；δiu是Kronecker函数；m是目标模型的聚类个数。

给定一个由N′个像素组成的中心坐标为y的候选目标图像区域，候选目标模型表达为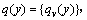 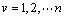，qv(y)按照下式定义

        (7)

其中：n是候选目标模型的聚类个数。

由于k均值聚类算法具有简单和快速的特点，本文采用k均值进行聚类计算。具体过程如下：在N个像素组成的聚类样本中先取m个聚类中心，计算每个聚类样本到这m个中心的距离，找到最小的距离并把该样本归入最近的样本的中心；然后修改中心点的值为本类所有样本的均值，再计算各个样本到m个中心的距离，重新归类，计算新的中心点，不断重复，直到新的聚类中心等于上一次的中心点。本文的K均值聚类终止的条件由迭代次数决定。

实验中对目标分成对称的4个区域，分别对每一块区域进行聚类操作。最后将每一个区域得到的pu或qv(y)的分布按照同样的顺序拼接起来，得到整个目标区域的聚类分布。

2.2  EMD度量

图像的相似性度量[4]用图像之间的距离表示，距离越大，图像之间的差别越大。其中有二次距离、卡方距离、Bhattacharyya距离等。但就本质而言，这些度量方法可以分为两类：一一映射法和交叉映射法。一一映射法测距要求两幅图像的直方图簇数与颜色句柄的长度须相等。一一映射和交叉映射都存在明显的不足。一一映射只计算对应簇的差别，而相似的两个点可能被划分到不同的两个簇中，从而无法得到比较。交叉映射法计算任意两个簇之间的差别，使得不应该进行比较的不相近点进行了比较，从而产生计算    误差。

Earth mover’s distance(简称EMD)距离[4]能很好地克服这些问题，它可以理解为从一种分布变换为另一种分布的最小代价，最早被Peleg，Werman和Rom介绍应用于计算机视觉问题。EMD的计算方法源于有名的运输问题，EMD的目的就是在两方之间寻找最小代价货物流，货物从供货商流向消费商，使得这些货物满足消费商的需求。据此，将EMD定义为：

簇集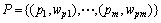由m个聚类组成，pi表示聚类，wpi是相应聚类的权值；簇集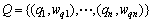由n个聚类组成，qj表示聚类，wqj是相应聚类的权值。Distij是聚类pi和qj之间的基本距离，fij是聚类pi和qj之间的“搬运量”，使得总消耗如式所示为最小：

         (8)

约束条件：

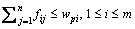
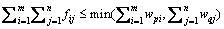
约束(8.1)保证从P到Q的“搬运”是不可逆的；约束(8.2)限制从P能“搬运”的量不能大于其权值的总和；约束(8.3)限制“搬运”到Q的量不能大于其权值的总和；约束(8.4)限制最大的“搬运”总量。其中，基本距离用来表示运输单位质量的货物所需要的工作量，本文选用CV_DIST_L1作为基本距离。

可以看出，不难把图像相似性度量问题转化为EMD的问题。当测量两幅图像的距离时，只要将其中一幅图像的分布特征集映射为货物流的一方，将另一幅图像的分布特征集映射为货物流的另一方，则两幅

图像之间的距离，就是运输货物所需要的最小代价。

2.3  似然函数

鉴于两个模型的分布是由聚类得到的，这样两幅图像的直方图簇数与颜色句柄的长度不一定相等，只能采用EMD进行两个分布的度量。

假设直方图的分布由(R，G，B，W)构成，将其转化成signature数组[2]。这样，对于一维直方图来说，signature数组的每行数据依次代表直方图的权值和直方图在(R，G，B)处的索引，signature数组列的数目代表聚类的个数。则两个分布之间的EMD距离D，由OpenCV中的EMD函数cvClacEMD2()[5]计算得到。

根据两个颜色聚类直方图模型之间的EMD距离，可以定义颜色聚类直方图模型之间的似然函数p(yk|xk)为

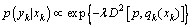      (9)

其中：p代表目标模板的颜色聚类直方图；qk(xk)代表k时刻目标侯选区域的颜色聚类直方图；D[p,qk(xk)]是p和qk(xk)的函数，代表直方图的距离。

3  似然函数的更新

在运动目标的跟踪中，目标可能发生各种各样的变化，如形变，光照的变化，遮挡等，如果模板一直得不到更新，跟踪的结果可能由于目标发生了各种变化而导致跟踪失败，因此如何更新模板是跟踪过程主要考虑的问题之一。基于K均值聚类得到的目标模型的描述，可以用在线K均值聚类不断地更新模板。基本思想如下：

When需要更新模板

For  pixel=1:N

If xpixel is closest to centeru

标记xpixel类别为u

End  For

计算N个xpixel的聚类中心add_centeru

new_centeru=α×old_centeru+(1-α)×add_centeru

centeru=new_centeru

其中，centeru表示第u类的中心向量。实验中α=0.95，每隔10帧，对模板直方图进行更新。更新的方法是，将前一帧似然函数最大的目标区域作为新的样本，按照上述在线K均值聚类的基本思想，找到与新样本最近的归属类，并将其按照一个贡献因子α加入所属的聚类中，使得原始的聚类直方图得到改变。由此计算模型间的似然函数也就得到了更新。

4  GPU加速

为了使跟踪算法满足实时性的需求。本文对K均值聚类部分进行了并行化加速。随着GPU技术的发展，当前的GPU具有很强的并行计算能力。随着NVIDIA公司的CUDA开发平台的推出，CPU代码的移植成本大大降低，对于并行化较好的代码，可以将其移植到GPU上进行加速。

4.1  CUDA平台

CUDA[6]代表“计算统一设备架构”，是NVIDIA公司专为计算而发展的一套应用软件开发环境与工具软件。在CUDA中，GPU通过建立多个线程由每个线程完成一个子任务来实现计算任务的并行处理。同时CUDA对C语言做了少量适应GPU特性的扩展，不需要学习特殊的符号集。CUDA允许程序员定义一种内核(kernel)函数。在调用kernel时，它将由N个GPU的线程并行执行N次，从而比原来CPU执行的函数消耗更短的时间。

CUDA线程在执行过程中可以访问多种存储器空间的数据，开发人员必须根据存储器空间大小、速度以及只读性等各方面因素，选择合适的存储器。

CUDA代码在执行时由于只能访问显存，因此在执行前，必须提前将数据由内存传入显存，在GPU执行代码结束后，再将结果传回内存。由于GPU和CPU有限的带宽，数据在两者之间的传输代价将非常昂贵，因此应尽可能在GPU上实现整个算法，来减少数据在二者间的传输。

4.2  K均值聚类并行优化

实验中采用一款NVIDIA公司的GTX460显卡，它实际使用7组多处理器，每组处理器由48个流处理器组成，这48个流处理器能够同时从GPU内存中读取到数据进行相同的处理，并将处理结果保存到GPU内存中。

观察K均值聚类算法，整个过程可以分为2个部分：计算每个样本点到所有样本中心的距离，找到距离最近的样本中心；在获得所有样本点的归属中心后，将样本点归入对应的分类中，再计算新的样本中心。图像中像素作为三维特征空间中的样本点集在空间域是均匀分布的，所以K均值可以在空间域固定尺度取初始中心[7]。

本文作者主要利用GPU的texture、shared memory、registers内存完成粒子滤波下的K均值聚类算法(见图1)。

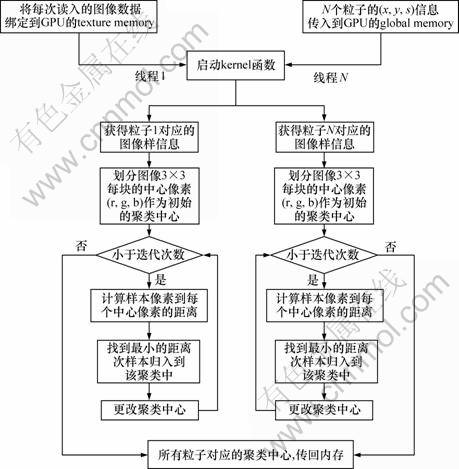
图1  GPU并行K均值算法流程图

Fig.1  Flow chart of GPU parallel K-means algorithm

5  实验结果

本文在CAVIAR Test Case Scenarios中的Clips from Shopping Center in Portugal库进行实验。实验环境为：NVIDIA公司的GTX 460。实验中，图像的大小为384×288，粒子数100。其中，RGB直方图的数目为8×8×8=512，采用Bhattacharyya距离度量相似程度，λ=20，跟踪结果用粉色的矩形框标注；K均值聚类数目为9，迭代次数为12，采用EMD距离度量相似程度，λ=170，跟踪结果用绿色矩形框标注，并加入每间隔10帧的模板更新。对所提出的在线K均值聚类跟踪算法与颜色直方图的跟踪算法[8]进行对比，实验结果如图2~4所示。

序列A中，跟踪目标的颜色与周围颜色相近，RGB直方图跟踪算法在序列253帧时，由于受到图片左边阴影的干扰，导致跟踪结果误差很大。序列B中，RGB直方图跟踪算法在270帧左右，由于受到图片左边阴影和过道阴影的干扰，跟踪结果逐渐偏离真实位置。序列C中，当遇到同样衣服的行人干扰时，RGB直方图跟踪算法跟踪失败。然而在这些情况下本文的算法，可以很好的跟踪目标，体现了算法的鲁棒性。通过计算跟踪区域的overlap _ratio(overlap_ratio=(目标的实际区域与算法的跟踪区域的交集)/ (目标的实际区域与算法的跟踪区域的并集))，进一步说明跟踪结果的准确性能(见图5)，其中，RGB直方图跟踪结果用实线表示，本文算法的跟踪结果用虚线表示。

经过GPU并行化处理K均值聚类部分，使得处理速度高于传统模式CPU速度的10倍左右，见表1。

表1  CPU和GPU的计算用时

Table 1  CPU and GPU for calculation of time

由表1可以看出，CPU的计算时间随着计算量的增长而线性增长。然而，GPU每个线程的计算时间是一定的，计算时间的增长仅仅与所需要更多的线程和内存与显存之间进行硬件的交互有关。

在保证跟踪准确度的前提下，增加粒子的数目，CPU与GPU处理每段视频的平均时间如图6所示。

图2  序列A的部分跟踪结果

Fig.2  Part of tracking results of sequence A

图3  序列B的部分跟踪结果

Fig.3  Part of tracking results of sequence B

图4  序列C的部分跟踪结果

Fig.4  Part of tracking results of sequence C

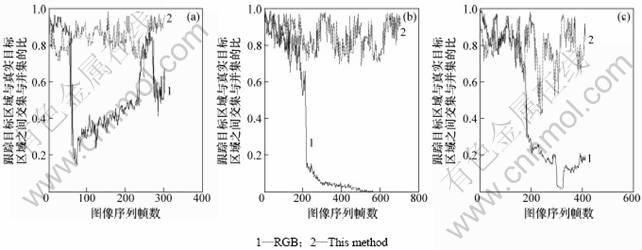
图5  序列A(a)、B(b)及C(c)的跟踪误差曲线

Fig.5  Tracking error curve of series A, B and C

图6  不同粒子数目下CPU和GPU处理序列A(a)、B(b)及C(c)的每一帧平均时间

Fig.6  Average time for each frame of CPU and GPU processing sequences A, B and C under different particle numbers

从图中曲线可以看出：随着粒子数目的增加，GPU处理的时间增长的缓慢，而CPU处理的时间呈现快速的线性增长。如序列A：当粒子数从100增长到900时，CPU处理的时间从328 ms增长到3.095 s，增长了约9.4倍。而GPU处理的时间从51.2 ms增长到424.7 ms，增长了约8.3倍。原来的加速比从6.4提高到了7.3。这些说明GPU并行化加速的优点。且随着计算复杂度的增加，GPU并行处理的优点比CPU更加突出。

6  结论

介绍了一种基于EMD度量的在线K均值聚类的目标跟踪方法，并用GPU对其K均值聚类部分并行化加速。在保证跟踪准确度的前提下，每帧图像的处理时间大约加速了10倍，满足视觉跟踪的实时性。同时实验结果表明，与原来的基于RGB颜色直方图的跟踪方法相比，具有更好的鲁棒性。但当目标变的比较小或目标与周围颜色相近的情况时，需要加入其他的目标特征，才能提高跟踪的准确性。

参考文献：

[1] 侯志强, 韩崇昭. 视觉跟踪技术综述[J]. 自动化学报, 2006, 32(4): 609-610.
HOU Zhi-qiang, HAN Chong-zhao. A survey of visual tracking[J]. Acta Automatica Sinica, 2006, 32(4): 609-610.

[2] QI Zhao, HAI Tao. Differential earth mover’s distance with its application to visual tracking[J]. IEEE Trans Pattern Analysis and Machine Intelligence, 2010, 32(2): 274-285.

[3] 程水英, 张剑云. 粒子滤波评述[J]. 宇航学报, 2008, 29(4): 1100-1103.
CHENG Shui-ying, ZHANG Jian-yun. Review on particle filters[J]. Journal of Astronautics, 2008, 29(4): 1100-1103.

[4] Rubner Y, Tomasi C, Guibas L. The earth mover’s distance as a metric for image retrieval[J]. International Journal of Computer Vision, 2004, 40(2): 99-121.

[5] 于仕琪, 刘瑞祯. 学习OpenCV教程[M]. 北京: 清华大学出版社, 2009: 231-233.
YU Shi-qi, LIU Rui-zhen. Learning openCV tutorial[M]. Beijing: Tsinghua University Press, 2009: 231-233.

[6] 张舒, 褚艳利. GPU高性能运算之CUDA[M]. 北京: 中国水利水电出版社, 2009: 14-76.
ZHANG Shu, CHU Yan-li. GPU computing for high performance-CUDA[M]. Beijing: China Water Power Press, 2009: 14-76.

[7] 陈加, 吴晓军, 蔡荣. GPU并行加速的均值偏移算法[J]. 计算机辅助设计与图形学报, 2010, 22(3): 463-464.
CHEN Jia, WU Xiao-jun, CAI Rong. Parallel processing for accelerated mean shift algorithm with GPU[J]. Journal of Computer-Aided Design & Computer Graphics, 2010, 22(3): 463-464.

[8] Perez P, Hue C, Vermaak J, et al. Color_based probabilistic tracking[J]. ECCV, 2002: 664-666.

(编辑 陈卫萍)

收稿日期：2011-04-15；修回日期：2011-06-15

基金项目：国家自然科学基金资助项目(90820304，61075027)；清华信息科学与技术国家实验室(筹)学科交叉基金资助项目(042003023)

通信作者：刘元元(1985-)，女，河北衡水人，硕士，从事视觉图像目标跟踪的研究；电话：15501026259；E-mail：liuyuanyuan1773@163.com