高压下Mg-5.88Zn-0.53Cu-0.16Zr合金凝固组织特征及其强化机制
来源期刊:中国有色金属学报(英文版)2020年第1期
论文作者:郭坤宇 徐畅 林小娉 叶杰 张冲 黄铎
文章页码:99 - 109
关键词:高压凝固;Mg-Zn-Cu-Zr合金;强化机制;共晶转变
Key words:high pressure solidification; Mg-Zn-Cu-Zr alloy; strengthening mechanism; eutectic transformation
摘 要:采用高压凝固技术,在2~6 GPa高压下对常规铸造Mg-5.88Zn-0.53Cu-0.16Zr合金进行凝固。利用SEM、EDS和XRD等手段研究高压凝固合金组织特征以及高压凝固实验合金室温压缩性能及其强化机制。结果表明,在高压作用下凝固,实验合金凝固组织得到显著细化,其二次枝晶间距由常压下的35 μm逐渐减小到6 GPa下的10 μm;在常压下,Mg(Zn)2、Mg7Zn3和MgZnCu共晶相连成网状分布在枝晶间;在高压下,晶间第二相 (Mg(Zn,Cu)2和Mg7Zn3相)多颗粒状或条状断续分布枝晶间。Zn和Cu在基体中的固溶度随凝固压力增加而增大,6 GPa下高达4.12%和0.32%。6 GPa下,实验合金的硬度高达HV 90,最大压断抗力为430 MPa。细晶强化、第二相强化及固溶强化是其强度提升的主要机制。
Abstract: Mg-5.88Zn-0.53Cu-0.16Zr (wt.%) alloy was solidified at 2-6 GPa using high-pressure solidification technology. The microstructure, strengthening mechanism and compressive properties at room temperature were studied using SEM and XRD. The results showed that the microstructure was refined and the secondary dendrite spacing changed from 35 μm at atmospheric pressure to 10 μm at 6 GPa gradually. Also, Mg(Zn,Cu)2 and MgZnCu eutectic phases were distributed in the shape of network, while under high pressures the second phases (Mg(Zn,Cu)2 and Mg7Zn3) were mainly granular or strip-like. The solid solubility of Zn and Cu in the matrix built up over increasing solidification pressure and reached 4.12% and 0.32% respectively at 6 GPa. The hardness value was HV 90 and the maximum compression resistance was 430 MPa. Therefore, the grain refinement strengthening, the second phase strengthening and the solid solution strengthening are the principal strengthening mechanisms.
Trans. Nonferrous Met. Soc. China 30(2020) 99-109
Kun-yu GUO1,2, Chang XU1,2, Xiao-ping LIN1,2,3, Jie YE1,2,3, Chong ZHANG1,2, Duo HUANG1,2
1. School of Resources and Materials, Northeastern University at Qinhuangdao, Qinhuangdao 066004, China;
2. School of Materials Science and Engineering, Northeastern University, Shenyang 110819, China;
3. Key Laboratory of Advanced Metal Materials and Forming Technology in Qinhuangdao, Northeastern University at Qinhuangdao, Qinhuangdao 066004, China
Received 30 March 2019; accepted 14 October 2019
Abstract: Mg-5.88Zn-0.53Cu-0.16Zr (wt.%) alloy was solidified at 2-6 GPa using high-pressure solidification technology. The microstructure, strengthening mechanism and compressive properties at room temperature were studied using SEM and XRD. The results showed that the microstructure was refined and the secondary dendrite spacing changed from 35 μm at atmospheric pressure to 10 μm at 6 GPa gradually. Also, Mg(Zn,Cu)2 and MgZnCu eutectic phases were distributed in the shape of network, while under high pressures the second phases (Mg(Zn,Cu)2 and Mg7Zn3) were mainly granular or strip-like. The solid solubility of Zn and Cu in the matrix built up over increasing solidification pressure and reached 4.12% and 0.32% respectively at 6 GPa. The hardness value was HV 90 and the maximum compression resistance was 430 MPa. Therefore, the grain refinement strengthening, the second phase strengthening and the solid solution strengthening are the principal strengthening mechanisms.
Key words: high pressure solidification; Mg-Zn-Cu-Zr alloy; strengthening mechanism; eutectic transformation
1 Introduction
Up to now, Mg-Zn-Cu alloy has been successfully commercialized as one kind of Mg-Zn heat-resistant alloy. It can be used in automobile engine parts and propellers [1,2] due to high temperature properties below 150 °C. Research shows that [3] good high temperature properties of Mg-Zn-Cu alloy are related to the existence of Cu in the eutectic phase Mg(Zn,Cu)2. However, the microstructure of the casting Mg-Zn-Cu alloy is coarse because the main strengthening phase (eutectic phase Mg(Zn,Cu)2) is distributed with a shape of network in the dendrites, which not only reduces the strengthening effect of Mg(Zn,Cu)2 phase, but also decreases the mechanical properties of the casting Mg-Zn-Cu alloy. Adversely, solidification characteristics of Mg-Zn-Cu-Zr systems are still not reported [4,5]. Therefore, to further improve the mechanical properties of Mg-Zn-Cu alloy and expand its applications, it is extremely important to refine the microstructure of Mg-Zn-Cu alloy and modify the morphology and distribution of Mg(Zn,Cu)2 eutectic phase.
High pressure solidification, one of the research fields of metal solidification under unusual conditions, has a significant effect on the solidification process and the microstructure of the alloys [6,7]. ZHANG [8] investigated the effects of the high-pressure solidification on the micro- structure and mechanical properties of Mg-6Zn-1Y. The results showed that the hardness value increased by about 41% compared with the conventional casting alloy, and the dimension of the second phase decreased to 50 nm under 6 GPa from 200 nm under atmospheric pressure. ZHOU et al [9] investigated the effects of high pressure on the solidification microstructure and mechanical properties of Mg-6Zn-1Y alloy and found that the microstructure of the alloy solidified under high pressure was significantly refined because of the combination of thermodynamic undercooling, composition undercooling and kinetic undercooling. The morphology of the intergranular eutectic second phase at 6 GPa was transformed from lamellar to granules and the hardness value of the alloy increased from HV 69 at atmospheric pressure to HV 97 at 6 GPa. LIN et al [10,11] investigated Mg96.17Zn3.15Y0.79Zr0.18 and Mg-6Zn-1Y under high pressure and pointed out the high-pressure solidification made contributions to refining the microstructure and improve the morphology and distribution of the second phase in the intergranular. Meanwhile, the solubility of Zn alloy increased and so did the compressive properties. The compressive strength of the experimental alloy promoted from 344 MPa at atmospheric pressure to 455 MPa and relative compressibility was changed from 16% to 25%. ZHANG et al [12] investigated the micro- structure of the Mg65Cu25Y10 alloy solidified under high pressure, the results showed that the new phase Cu2(Y,Mg) was formed at 2-5 GPa, and the size of Cu2(Y,Mg) phase decreased with the increasing solidification pressure, with the size of only 8 nm at 5 GPa. It can be seen that solidifying the alloy under high pressure is a new method [13-17] to refine the microstructure and improve the morphology and distribution of the second phase. Therefore, in this study, the CS-1B type cubic hinge press was used to solidify the coarse-grained Mg-6Zn-0.5Cu-0.2Zr alloy at 2, 4 and 6 GPa, respectively, which aimed at refining the microstructure of Mg-6Zn-0.5Cu-0.2Zr alloy and improving the morphology and distribution of the second phase so that the mechanical properties of the alloy can be promoted. On this basis, according to the existing alloy strength theories such as the grain refinement strengthening, the solid solution strengthening and the second phase strengthening, we can further explain the improvement mechanism of the mechanical properties of the magnesium alloy solidified under high pressure.
2 Experimental
The experimental Mg-Zn-Cu-Zr alloy was prepared by pure magnesium ingot (99.99 wt.% purity), pure zinc ingot (99.99 wt.% purity), Cu-Zn (7:3) brass, Mg-30Zr master alloy. The 2RRL-M8 vacuum resistance furnace was used for melting the alloy, with the melting temperature of 760 °C and the casting temperature of 730 °C. Then the alloy was put into the preheated metal mold for casting. The last constituents of the experimental alloy analyzed by ICAP 6300 plasma spectroscopy were listed as follows (wt.%): 5.88 Zn,0.53 Cu, 0.16 Zr with the rest of Mg. The ingots were homogenized and then cut into a cylinder with 6 mm in diameter and 8 mm in length. CS-1B high-pressure cubic press was used to do the high-pressure solidification experiments, whose working principle is to use the six hammer heads in the upper, lower, left and right, and three cubes to jointly squeeze the cube cavity from three directions to achieve quasi-static pressure as shown in Fig. 1.
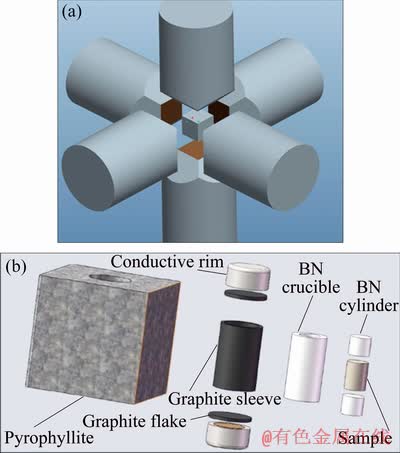
Fig. 1 Schematic diagrams of working principle of CS-1B type cubic hinge press (a) and high pressure solidified assembly set (b)
The solidification pressures were set to be 2, 4 and 6 GPa. Superheat temperature is one of the crucial factors affecting the thickness of the solidified alloy. Accurate and reasonable heating and melting temperature of the experimental alloy at high pressure is one of the key parameters to the ideal high pressure solidified samples. According to the Clausius-Clapeyren equation, the relationship between pressure and melting point [18] is
 (1)
(1)
where dT is the change of the melting temperature; dP is the corresponding change of pressure; Tm is the melting temperature (K); ΔV is the change of the solid-liquid phase transition volume; and ΔHm is the latent heat of crystallization (J/g). It can be viewed from the formula (1) that the melting temperature varies with the change of the solid-liquid phase volume. And the melting temperature of Mg rises in enlarging volume of Mg under applied pressure. To determine the liquidus temperatures of the experimental alloy, the samples were heated (insulation for 15 min) and then cooled to room temperature at different high pressures, finally the liquidus temperatures could be determined according to the change of the solidification microstructure. The results showed that the liquidus temperatures of the alloy at 2, 4 and 6 GPa were 760, 800 and 850 °C, respectively. According to the liquidus temperatures, the melting temperature was set to above the liquidus temperature of 30 °C so the overheat degree was 30 °C.
After that, the samples were taken into the assembled graphite sleeve as shown in Fig. 1, while the assembled graphite sleeve was taken into the cavity position of the high pressure cubic press. And then, to start the high-pressure solidification experiment [19], the hammer head should be placed towards the sample. First, the pressure was set to the presupposition pressure, at the same time the temperature measuring device was started and quickly heated to the preset heating temperature. Then the molten alloy was convened for 15 min before the power supply was turned off. Finally, the sample was collected off when the samples cooled down to room temperature.
The microstructure of the alloy and the energy spectrum analysis were examined using the Axio Scope A1 Pol optical microscope (OM), SUPRA- 55 scanning electron microscope (SEM) and energy depressive spectroscopy (EDS). The phase analysis was performed using a 2500/PC type XRD with a scanning step size of 0.3°, and an XRD diffraction spectrum was measured between 20° and 90°(2q). According to GB/T6394-2002, the interception method determining the average grain size of metal was employed to measure the dimension of “dendritic cluster”, that is the “dendritic cluster” size is determined by counting the number of grain boundary cut points for a given length. The average value of the intercept on the test surface of the sample can be calculated according to the formula (2):
l=L/(MN) (2)
where L is the length of the measuring line segment (mm); l is the average intercept on the test surface; M is the magnification power of the microscope; N is the number of intercept points on the measurement grid. In order to increase the accuracy, this experiment measures 10 fields of view at 50x and 100x respectively and takes the average value as the sample grain size.
The volume fraction of the second phase was counted by Image-Pro-Plus image analysis software. The hardness of the experimental alloy was tested using a HV-1000A micro Vickers hardness tester with loads of 49 N (5 kg) and 0.098 N (10 g). WDW3100 computer control electronic universal testing machine was used for compression experiments at room temperature at a strain rate of 0.001 s-1. During the compression process, the computerized data logger attached to the universal test machine automatically collected stress and strain data.
3 Results and analysis
3.1 Refinement mechanism
Figure 2 shows the optical microstructure (OM) of the experimental alloys during solidification. According to Fig. 2(a), coarse dendrite exhibits in primary grain α-Mg with an average size of 345 μm, and the secondary dendrite spacing is about 35 μm. And from Figs. 2(b-d), the microstructure is significantly refined. At the same time, the morphology of dendrite is more regular and complete. Also, there is less phenomenon of dendritic fracture and fragmentation with increasing solidification pressure.
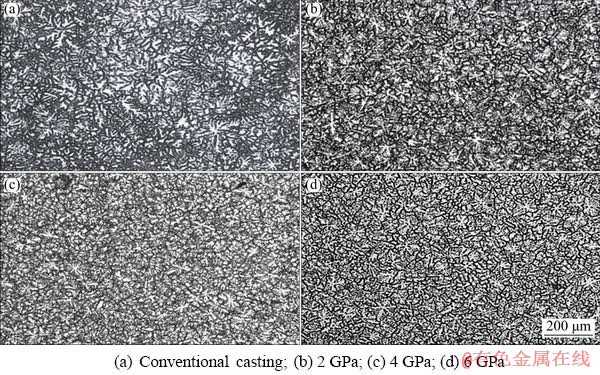
Fig. 2 Optical microstructures of experimental alloys solidified under different pressures
The average sizes of dendrites solidified at 2, 4 and 6 GPa are found to be 80, 65 and 60 μm, respectively. The secondary dendrite spacings are 15, 12 and 10 μm, respectively. From atmospheric pressure to 2 GPa, the average size of dendritic and the secondary dendrite spacing are refined, and the original sizes are 4.3 times and 2.3 times the current size, respectively. From 2 to 6 GPa, the original sizes are 1.3 times and 1.5 times the current size, respectively. Thus, it is mainly the reduction of the average size of dendritic during solidification from atmospheric pressure to 2 GPa and it is mainly the decrease of secondary dendrite spacing from 2 to 6 GPa. In addition, the number of crystal nuclei increases during high-pressure solidification compared with the dendritic number at different pressures in Fig. 2. The number of crystal nuclei per unit area reaches 248 at 6 GPa from 8 at atmospheric pressure.
According to the high-pressure solidification theory, considering the influence of pressure on the solidification process and the relationship between critical radius and pressure and relationship between critical nucleation work and pressure can be expressed as [20]
 (3)
(3)
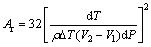 (4)
(4)
where rk is the critical radius; σ is the specific surface energy; Ar is the critical nucleation work; ρ is the density of the alloy; ΔT is supercooling temperature; V1 is the volume of the solid alloy; V2 is the volume of the melting alloy; dP is the pressure, according to Eqs. (3) and (4), the pressure is inversely proportional to the critical nucleation radius and the critical nucleation energy. That is, applying the solidification pressure can increase the number of crystal nuclei. Meanwhile, high pressure increases the diffusion activation energy and then inhibits atomic diffusion to increase the activation energy of crystal growth and decrease the crystal growth rate [21]. The high number of nuclei and the slow crystal growth rate contribute to obtaining a fine equiaxed grain microstructure of the experimental alloy solidified under high pressure.
Figure 3 shows the SEM images of the experimental alloys. It can be seen from Fig. 3(a) that the second phases in the microstructure are mostly in the form of a long island or “layered eutectic” (Fig. 3(b)) which is connected into a network of segregation between the α-Mg dendrites. In addition, a few granular second phases are also distributed in the dendrites and the volume fraction of the second phase is 35%. After solidification under high pressure, as shown in Figs. 3(c)-(f), the network of the second phase is gradually broken. The inter-crystalline second phase in the form of “layered eutectic” gradually decreases, and the area of eutectic structure of the trigeminal grain boundaries also decreases. The above phenomenon can be clearly observed from the comparison of the morphology and size of the “eutectic structure” at the trigeminal grain boundary between the conventional casting alloy and the experimental alloy solidified under 6 GPa pressure in Fig. 4. The area of the “eutectic structure” at the trigeminal grain boundaries of the experimental alloy at 6 GPa is significantly smaller than that of the conventional casting alloy (shown by the circles in Fig. 4), at the same time, the solid strip (rod-like) or granular second phases gradually increased. Figure 3(e) shows that the proportion of the particulate intergranular second phase at 6 GPa exceeds that of the strip second phase. While the solid strip of the second phase (Fig. 3(f)) exhibits “divorced eutectic” microstructure, that is, the eutectic transformation of the experimental alloy is gradually converted from a symbiotic eutectic under atmospheric pressure to a divorced eutectic at 6 GPa. The volume fraction of the second phase gradually decreases with the increasing solidification pressure, which is reduced from 25% at 2 GPa to 20% at 6 GPa.

Fig. 3 SEM images of experimental alloy solidified under different pressures
Figure 5 shows the distribution of solute atoms Zn and Cu in solidified microstructure under different pressures (SEM). According to Figs. 5(a) and (b) that at atmospheric pressure, Zn and Cu atoms are mostly segregated in the α-Mg dendrites, and the distribution intensity in the matrix is relatively low. At 2 GPa, the Zn strength near the second phase is significantly increased (Fig. 5(c)), that is, the solubility of Zn in the α-Mg matrix increases; and the distribution intensity of Cu in the α-Mg matrix also increases (Fig. 5(d)). As the pressure increases, the solubility of Zn and Cu in the α-Mg matrix increases.
As shown in Fig. 6, when the pressure reaches 6 GPa, the distribution intensity and uniformity of Zn in the α-Mg matrix are significantly increased, and Zn-rich granule phase is formed inside the dendritic cluster. (Fig. 6(a)). While the distribution intensity and uniformity of Cu in the α-Mg matrix are even higher than Zn(Fig. 6(b)).
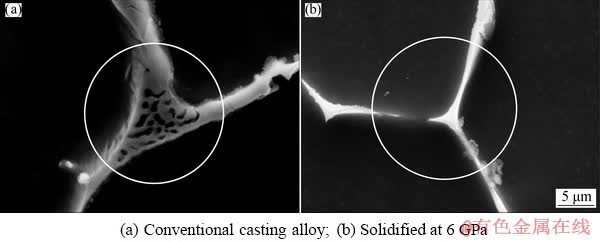
Fig. 4 SEM images of eutectic structure at trigeminal boundary of experimental alloy
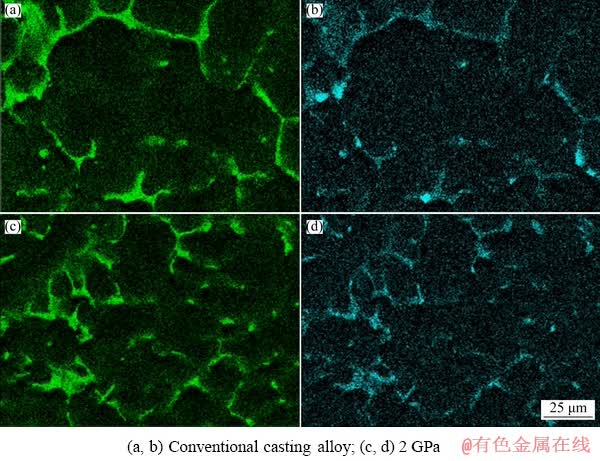
Fig. 5 Effect of solidification pressure on distribution in matrix of Zn (a, c) and Cu (b, d)
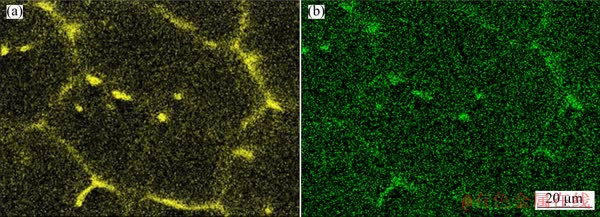
Fig. 6 Distribution in matrix of Zn (a) and Cu (b) at 6 GPa
The EDS was used to test the element content of the internal matrix of the grain, the results showed that in the conventional casting experimental alloy, the solid solubility of Zn in the α-Mg matrix was about 2.28% (mass fraction, the same below), and that of Cu in the α-Mg matrix was relatively low, about 0.1%, as shown in spectrogram 1of Fig. 3(b). At 2 GPa, the solid solubility of Zn increased to 3.05%, which was significantly higher than that at atmospheric pressure; however, that of Cu increased slightly to 0.16%. At 4 and 6 GPa, the solid solubilities of Zn in the α-Mg matrix were 3.45% and 4.12%, respectively, and the solid solubilities of Cu in the α-Mg matrix were 0.24% and 0.32%, respectively.
The dynamic viscosity of the melt at atmospheric pressure is η0, and the dynamic viscosity [22] under pressure P is
ηp=η0exp[(E+PVNA)/kT] (5)
where E is the viscous rheological activation energy; V is the volume; k is the Boltzmann constant; NA is the Avogadro constant; T is the temperature. It is known from the formula (5) that the viscosity of the melt increases as the pressure increases. According to the existing high-pressure solidification theory, when solidified under high pressure, the increase of melt viscosity will have a great influence on the diffusion of solute atoms in the liquid phase.
The relationship between pressure and solute diffusion coefficient (D) can be expressed by [23]
D=RTδ-1η-1=RTδ-1η0-1exp[-(PV0/(RT))] (6)
where R is the molar gas constant, 8.314 J/(K×mol); T is the melt temperature, K; δ is the atomic free stroke length, mm; η is the viscosity of the solution, Pa×s; V0 is the original molar volume of the liquid phase. Solidification under high pressure can simplify Eq. (6) to
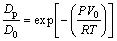 (7)
(7)
where Dp is the diffusion coefficient under different pressure and D0 is the diffusion constant.
According to Eq. (7), the atomic diffusion coefficient of the solute decays exponentially with increasing pressure. That is, when solidified under high pressure, the diffusion coefficient of solute atoms such as Cu and Zn exponentially decays, especially when it reaches 6 GPa. The diffusion of Cu atoms during solidification is very difficult, and the redistribution of solute atoms is weakened. As a result, the degree of segregation is reduced; while the solute redistribution of Zn is also weakened, more Zn atoms are dissolved in the matrix, and Zn which is segregated between the dendrites is decreased.
Under atmospheric pressure, there are two kinds of mole fractions of Mg, Zn and Cu in the second phase. Among them, a kind of the second phase in Fig. 3(b) has a small content of Cu (1.12-1.35 at.%) after measurement, which is a solid solution of Mg-Zn binary phase of Cu. Another kind of the second phase has a higher Cu content, accounting for (20±4) at.%, which is Mg-Zn-Cu ternary phase. Referring to the XRD patterns in Fig. 7, it is found that the experimental alloy consists of α-Mg, MgZn2, CuMgZn phases under atmospheric pressure.
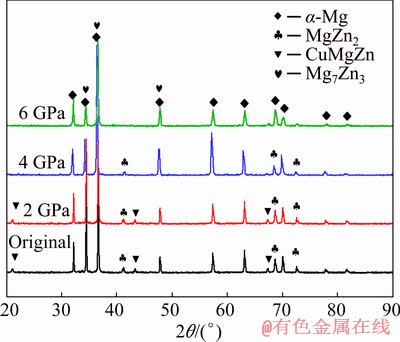
Fig. 7 XRD patterns of experimental alloy under different pressures
The redistribution of Cu and Zn solute atoms during solidification under high pressure is weakened, resulting in a change in the second phase microstructure. It can be seen from Fig. 7 that the characteristic diffraction peak of CuMgZn phase can be observed at 2 GPa, which is hardly observed at 4-6 GPa; the characteristic diffraction peak of MgZn2 phase also decreases with the increasing pressure and it can be observed at 4 GPa. At 6 GPa, the peak strength is weaker. From the diffraction pattern at 6 GPa, it is known that the diffraction peak of Mg7Zn3 phase with low Zn/Mg appears, which is consistent with the distribution law of Zn and Cu solute atoms in the matrix and the analysis of solid solubility change.
Therefore, Zn and Cu are mostly segregated between α-Mg dendrites under atmospheric pressure, and a “lamellar” eutectic phase MgZn2, Mg7Zn3 phase (solid solution of a few Cu) and a rod-shaped CuMgZn phase are formed by the symbiotic eutectic transformation. Zn and Cu atoms gradually dissolve into the matrix as the solidification pressure increases, resulting in the low degree of segregation and reduced atomic fraction in the second phase. At 6 GPa, a “solid” thin strip and granular MgZn2 and Mg7Zn3 eutectic phases are constituted divorced eutectic transformation.
3.2 Mechanical properties
3.2.1 Hardness
The hardness value of the conventional casting experimental alloy is HV 41. At 2 GPa, the hardness rises to HV 50, an increase of 22.9% compared to the conventional casting alloy. The hardness of the experimental alloy increases with the increasing solidification pressure. At 4 and 6 GPa, the hardness values of the experimental alloy are HV 71 and HV 90, respectively. The hardness of the experimental alloy at 6 GPa is 123% higher than that of the conventional casting alloy.
3.2.2 Compressive properties
Figure 8(a) shows the stress-strain curves of the experimental alloy at room temperature. Figure 8(b) shows the mechanical properties with solidification pressure. According to Fig. 8(a), the compressive strength (σb) is 170 MPa, the yield strength (σs) is 160 MPa and the relative compressibility (δ) is 11.23%. When solidified at 2, 4 and 6 GPa, σb are 320, 380 and 430 MPa, respectively, σs are 280, 320 and 370 MPa, respectively, and δ are 18.32%, 17.54% and 14.48%, respectively.
According to Fig. 8(b), the relative compressibility (δ) of the experimental alloy first increases and then decreases with the increasing solidification pressure. The maximum δ is 18.32% at 2 GPa and decreases to 14.48% when solidified at 6 GPa. The σb and σs of the experimental alloy gradually increase with the increasing solidification pressure, but the growth slope is the largest from the atmospheric pressure to the 2 GPa stage. At 2 GPa, σb and σs of the experimental alloys are increased by 88.24% and 75%, respectively. At 6 GPa, the strengths of the experimental alloys are further increased by 34.38% and 32.14% compared with those at 2 GPa.
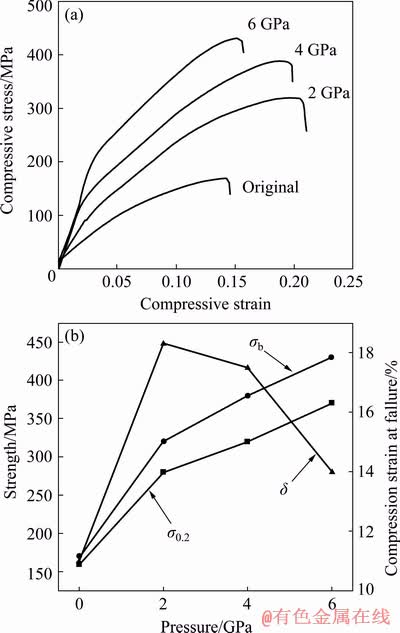
Fig. 8 Room temperature compressive stress-strain curve of experimental alloy (a) and mechanical properties with solidification pressure (b)
Material strength is extremely sensitive to the composition and microstructure. The strengthening mechanisms for magnesium alloy without heat treatment are: the grain refinement strengthening, the solid solution strengthening and the second phase dispersion strengthening. And the grain refinement strengthening can be described by the Hall-Petch equation [23]:
ss=s0+k0d-1/2 (8)
where s0 is the frictional force to prevent dislocation slip, a constant independent of the grain size; k0 is the grain boundary resistance, a constant related to the crystal type; d is the average grain size of the alloy. The second term in Eq. (8) reflects the grain boundary strengthening effect. While in magnesium alloy, k0≈280-320 MPa·mm1/2 [17,23] which is 4-5 times that of the Al alloy (kAl≈68 MPa·μm1/2). Therefore, the strengthening effect of magnesium alloy due to grain refinement is extremely significant. For equiaxed crystals, the secondary dendrite spacing is the primary determinant of the grain refinement strengthening. The above experimental results demonstrate that the secondary dendrite spacing of the experimental alloy decreases with the increasing solidification pressure. The secondary dendrite spacing is gradually reduced from 35 μm under conventional casting to 15, 12 and 10 μm at 2, 4 and 6 GPa. The k0d-1/2 (k0≈300 MPa·mm1/2) can be used to roughly calculate the strengths increase by the decrease of the secondary dendrite spacing: 78, 87 and 95 MPa, respectively, and the contribution rates are 52.00%, 41.43% and 36.54%, respectively. That is, from atmospheric pressure to 2 GPa, the strength increase due to the decrease in grain size is the largest.
Solid solution strengthening can be described by [24]
σs∝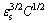 (9)
(9)
where σs is the yield strength of the alloy; εs is the mismatch strain caused by the difference between the solute atom and the solvent atom radius; C is the solute atom concentration. It can be seen that εs and C are the main factors affecting the solid solution strengthening effect. The difference between the atomic sizes of Zn and Mg is 16% and that of Cu and Mg is 20%. Therefore, when Zn and Cu are solid-dissolved into the α-Mg matrix, lattice distortion will occur, and the resulting stress field will hinder dislocation motion and then produce solid solution strengthening. The solid solubilities (wt.%) of Zn and Cu in α-Mg matrix under atmospheric pressures of 2, 4 and 6 GPa are 2.28% and 0.10%, 3.05% and 0.16%, 3.45% and 0.24%, 4.12% and 0.32%, respectively. Studies have shown that [16], every 1 wt.% solid solubility of Zn and Cu in the α-Mg matrix increases, the solid solution strengthening increases by 45 and 35 MPa. It can be seen that during solidification at 2, 4 and 6 GPa, the strength increasing values due to the increased solid solutions of Zn and Cu are about 37, 58 and 90 MPa, respectively. The values are about 24.67%, 27.62% and 34.62% of the total increase in the strength of the experimental alloy.
In addition, micro-hardnesses of the experimental alloy matrix under different solidification pressures were tested. The results showed that the matrix hardness of the conventional casting experimental alloy was HV 34, and those at 2, 4 and 6 GPa were HV 44, HV 62 and HV 78, respectively, which were 29.41%, 82.35% and 129.41% higher than that of the conventional casting experimental alloy. It can be seen that the contribution of solid solution strengthening at 4 and 6 GPa to the improvement of alloy properties is very large.
According to the Orowan equation [25]:
Δτ∝[f 1/2(r/b)]/r (10)
where f is the volume of the precipitated phase; r is the radius of the precipitated particles. The second phase enhancement effect is closely related to the size of the second phase particle. In the solidification microstructure of conventional casting alloy, the main strengthening phases were mostly distributed in the form of “lamellar” eutectic or rod-like network, which disconnected the microstructure of the matrix. When solidified at 2 GPa, the network formed by the second phase was gradually broken, and the granular or island-like second phase was significantly increased compared with the conventional casting alloy. At 6 GPa, a large number of granular second phases were distributed on the matrix, and only a small number of broken strip-shaped second phases were present. In this way, while the matrix action can be fully exerted, the granular or long island-like strengthening phase will strongly interact with the dislocation during the compression process, and the dislocation motion is hindered, therefore, the second phase strengthening becomes the main mechanism for improving the mechanical properties of the high-pressure solidified alloy.
To sum up, the contribution of grain refinement strengthening is the largest under 2 GPa during solidification, so the strength of the experimental alloy is improved and the plasticity is also improved. As the solidification pressure increases, especially at 6 GPa, solid solution strengthening and the second phase strengthening also become the main mechanisms of strengthening, so the alloy strength is greatly improved while the plasticity is decreased.
4 Conclusions
(1) The primary dendrites α-Mg of the alloy under high pressure were mostly uniform equiaxed grains. The number of crystal nuclei per unit area gradually increased with the increasing solidification pressure and the secondary dendrite spacing gradually decreased, from 35 μm under atmospheric pressure to 10 μm at 6 GPa. The solid solubility of Zn and Cu in the α-Mg matrix also increased, from 2.28% and 0.10% at atmospheric pressure to 4.12% and 0.32% at 6 GPa, respectively.
(2) The second phases in the solidification microstructure of the conventional casting experimental alloy were mostly in the form of long island or “layered eutectic”, which is connected into the network of a-Mg dendrites. And the second phases were mainly Cu-rich MgZn2, Mg7Zn3 and CuMgZn phases. While at 6 GPa, the second phase was primarily a strip-like or granular Mg7Zn3 and MgZn2 phases.
(3) The maximum crushing resistance (σb) of the conventionally casting experimental alloy at room temperature was 170 MPa, and the relative compressibility (δ) was 11.23%. While solidified under high pressure, the strength of the experimental alloy increased with the increasing solidification pressure. The σb at 6 GPa increased to 430 MPa, but the change of δ was not large (14.48%). The mechanism during solidification at 6 GPa is mainly the fine grain strengthening caused by the secondary dendrite spacing refinement, the solid solution strengthening caused by the increased solid solubility of Zn and Cu in the matrix and the second phase enhancement resulting from strong interaction of much granular second phases with dislocations.
References
[1] LI Guo-qiang, ZHANG Jing-huai, WU Rui-zhi, FENG Yan, LIU Shu-juan, WANG Xiao-jun, JIAO Yu-feng, YANG Qiang, MENG Jian. Development of high mechanical properties and moderate thermal conductivity cast Mg alloy with multiple RE via heat treatment [J]. Journal of Materials Science & Technology, 2018, 34(7): 1076-1084.
[2] SWETHA CHOWDARY V, RAVIKUMAR D, ANAND KUMAR S, KONDAIAH V V, RATNA SUNIL B. Influence of heat treatment on the machinability and corrosion behavior of AZ91 Mg alloy [J]. Journal of Magnesium and Alloys, 2018, 6(1): 52-58.
[3] DONG Qing, ZHE Zhu-Hong, WANG Le-yun, YING Tao, JIN Zhao-hui, LI De-jiang, DING Wen-jiang, ZENG Xiao-qin. Basal- plane stacking-fault energies of Mg alloys: A first-principles study of metallic alloying effects [J]. Journal of Materials Science & Technology, 2018, 34(10): 1773-1780.
[4] HUANG L, LIU S H, DU Y. Thermal conductivity of the Mg-Al-Zn alloys: Experimental measurement and CALPHAD modeling [J]. Calphad-computer Coupling of Phase Diagrams & Thermochemistry, 2018, 62: 99-108.
[5] WANG Zhi, ZHOU Ye, LI Yi-zhou, WANG Feng, LIU Zheng, MAO Ping-li, JIANG Xiao-ping. Hot tearing behaviors and in-situ thermal analysis of Mg-7Zn-xCu- 0.6Zr alloys [J]. Transactions of Nonferrous Metals Society of China, 2018, 28(8): 1504-1513.
[6] YAO B, DING B Z, HU Z L. Effect of static high pressure on formation and grain size of bulk nano Pd-Si-Cu alloys [J]. Chinese Science Bulletin, 1994, 39(18): 1656-1657.
[7] LI D J, DING B Z, HU Z L. Direct formation of bulk Cu-Ti nano crystalline alloys-high temperature solid phase quenching under high pressure [J]. Chinese Science Bulletin, 1994, 39(19): 1749-1751.
[8] ZHANG L. High pressure solidification microstructure and phase evolution of Mg-Zn-Y magnesium alloy [D]. Shenyang: Northeastern University, 2011. (in Chinese)
[9] ZHOU H T, LIU K M, ZHANG L. Influence of high pressure during solidification on the microstructure and strength of Mg-Zn-Y alloys [J]. Journal of Rare Earths, 2016, 34(4): 435-440.
[10] FAN Z B, LIN X P, DONG Y. Dynamic recrystallization kinetic of fine grained Mg-Zn-Y-Zr alloy solidified under high pressure [J]. Journal of Rare Earths, 2017, 35(9): 920-926.
[11] DONG Y, LIN X P, XU R. Microstructure and compression deformation behavior in the quasi-crystal reinforced Mg-8Zn-1Y alloy solidified under super-high pressure [J]. Journal of Rare Earths, 2014, 32(11): 1048-1055.
[12] ZHANG J, ZHANG H F, DONG P. Formation and thermal stability of nanoscale Cu2(Y, Mg) during the solidification of Mg65Cu25Y10 alloy under high pressure condition [J]. Acta Metallurgica Sinica, 2004, 40(2): 211-214.
[13] CHEN J Y, ZHENG H F, ZENG Y C. High pressure—A new technology in modern science [J]. Scientific and Technical Information, 2000, 18(8): 22-24.
[14] ZHAO S, PENG Q, LI H. Effects of super-high pressure on microstructures, nano-mechanical behaviors and corrosion properties of Mg-Al alloys [J]. Journal of Alloys & Compounds, 2014, 584(3): 56-62.
[15] CHENG L U, ZHANG S, ZHANG Y U. Insights into structural and thermodynamic properties of the intermetallic compound in ternary Mg-Zn-Cu alloy under high pressure and high temperature [J]. Journal of Alloys & Compounds, 2014, 597(6): 119-123.
[16] HANSTROM A, LAZOR P. High pressure melting and equation of state of aluminium [J]. Journal of Alloys & Compounds, 2000, 305(1): 209-215. (in Swedish)
[17] GUO X F. Refined Mg alloys and their microstructures and properties [M]. Beijing: Metallurgical Industry Press, 2010. (in Chinese)
[18] БATHШEB А И. Crystallization of metal and alloys under pressure [M]. ZHANG J S, trasl. Harbin: Harbin University of Technology Press, 1987. (in Chinese)
[19] LIN X P, DONG Y, XU R. Solidification microstructures and crystalline morphologies of Mg-6Zn-1Y alloy solidified under GPa level super-high pressure [J]. Rare Metal Materials and Engineering, 2013, 42(11): 2309-2314.
[20] LI R X, LI R D, BAI Y H. Effect of specific pressure on microstructure and mechanical properties of squeeze casting ZA27 alloy [J]. Transactions of Nonferrous Metals Society of China, 2010, 20(1): 59-63.
[21] LI R D, CAO X S, QU Y D. Effect of super high pressure on crystal structure and microstructure of ZA27 alloy [J]. Transactions of Nonferrous Metals Society of China, 2009, 19(9): 1570-1574.
[22] CHEN Zhen-hua, XIA Wei-jun, YAN Hong-ge. Principles and technologies of plastic deformation for magnesium alloys [J]. Chemical Industry and Engineering Progress, 2004, 23(2): 127-135.
[23] DING W J. Magnesium alloy science and technology [M]. Beijing: Science Press, 2007. (in Chinese)
[24] SUZUKI M, SATO H, MARUYAMA K. Creep deformation behavior and dislocation substructures of Mg-Y binary alloys [J]. Materials Science and Engineering A, 2001, 319(1): 751-755. (in Japanese)
[25] YONG Q L. Second phase in steel materials [M]. Beijing: Metallurgical Industry Press, 2006. (in Chinese).
郭坤宇1,2,徐 畅1,2,林小娉1,2,3,叶 杰1,2,3,张 冲1,2,黄 铎1,2
1. 东北大学秦皇岛分校 资源与材料学院,秦皇岛 066004;
2. 东北大学 材料科学与工程学院,沈阳 110819;
3. 东北大学秦皇岛分校 秦皇岛市先进金属材料及成型技术重点实验室,秦皇岛 066004
摘 要:采用高压凝固技术,在2~6 GPa高压下对常规铸造Mg-5.88Zn-0.53Cu-0.16Zr合金进行凝固。利用SEM、EDS和XRD等手段研究高压凝固合金组织特征以及高压凝固实验合金室温压缩性能及其强化机制。结果表明,在高压作用下凝固,实验合金凝固组织得到显著细化,其二次枝晶间距由常压下的35 μm逐渐减小到6 GPa下的10 μm;在常压下,Mg(Zn)2、Mg7Zn3和MgZnCu共晶相连成网状分布在枝晶间;在高压下,晶间第二相 (Mg(Zn,Cu)2和Mg7Zn3相)多颗粒状或条状断续分布枝晶间。Zn和Cu在基体中的固溶度随凝固压力增加而增大,6 GPa下高达4.12%和0.32%。6 GPa下,实验合金的硬度高达HV 90,最大压断抗力为430 MPa。细晶强化、第二相强化及固溶强化是其强度提升的主要机制。
关键词:高压凝固;Mg-Zn-Cu-Zr合金;强化机制;共晶转变
(Edited by Xiang-qun LI)
Foundation item: Projects (51675092, 51775099) supported by the National Natural Science Foundation of China; Projects (E2018501030, E2018501033, E2018501032) supported by the Natural Science Foundation of Hebei Province, China
Corresponding author: Xiao-ping LIN; Tel: +86-13780356091; E-mail: lxping3588@163.com
DOI: 10.1016/S1003-6326(19)65183-6

