
DOI: 10.11817/j.issn.1672-7207.2021.02.033
高阶多边形车轮的瞬态磨耗行为分析
黄双超,赵鑫,张笃超,许黎明,温泽峰,金学松
(西南交通大学 牵引动力国家重点实验室,四川 成都,610031)
摘要:采用ANSYS/LS-DYNA建立自由轮对运行于半径3 500 m曲线轨道上的三维轮轨滚动接触有限元模型,于时域内模拟考虑轮对初始横移和侧滚角的高速曲线通过和瞬态滚滑行为,分析不同牵引系数下23阶实测车轮多边形对轮对曲线通过和车轮瞬态磨耗的影响。研究结果表明:车轮多边形会造成轮轨力、法/切向接触应力、摩擦功和磨耗深度等的周期性波动,最终造成非均匀磨耗;当速度为250 km/h和牵引系数为0.03时,峰谷幅值为0.128 mm的车轮多边形可使最大垂向轮轨力达113 kN(静态轮重的144%),摩擦功最大值可由平顺表面下的2 mJ增至2.3 mJ,相应波动幅值可达1.4 mJ;虽然一侧车轮多边形所激励的振动可以传递至另一侧,但对另一侧车轮多边形的发展不起主导作用;多边形造成的磨耗率峰值、谷值分别发生在多边形幅值的波峰、波谷附近,会抑制车轮多边形的进一步发展;牵引系数增大,会加剧车轮表面的平均磨耗和非均匀磨耗,加速车轮多边形的发展。
关键词:高速动车组;高阶多边形;轮轨滚动接触;非均匀磨耗;显式有限元
中图分类号:U211.5 文献标志码:A 开放科学(资源服务)标识码(OSID)
文章编号:1672-7207(2021)02-0648-11
Analysis on transient wear of high-order polygonal wheels
HUANG Shuangchao, ZHAO Xin, ZHANG Duchao, XU Liming, WEN Zefeng, JIN Xuesong
(State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China)
Abstract: A three-dimensional wheel-rail rolling contact finite element(FE) model was developed by ANSYS/LS-DYNA to simulate the high speed curving of a free wheelset on a curve of radius of 3 500 m and the rolling-sliding behavior between wheel and rail in the time domain. The lateral shift and roll of the wheelset were set as initial conditions. The influence of measured 23-order polygons on the high speed curving and transient wear on the wheels at different traction coefficients was analyzed. The results show that the wheel polygons can lead to significant periodic variations of wheel and rail contact forces, contact stresses, friction work and worn depth, causing uneven wear. At 250 km/h and a traction coefficient of 0.03, due to the existence of the wheel polygons with a peak and valley amplitude of 0.128 mm, the maximum vertical wheel-rail force reaches 113 kN (144% of the static wheel load), the maximum frictional work reaches 2.3 mJ from 2.0 mJ on the even surfaces, and a fluctuation up to 1.4 mJ is present. Although the vibrations excited by the polygon on one side can be transferred to the other side, it does not play a dominant role in the development of the polygon on the other side. The peak wear rate and least wear rate occur near the geometric crest and valley of polygons respectively,prohibiting further development of the polygons. The increase of traction coefficient will increase the average wear and uneven wear of the wheel surface, accelerating the development of the wheel polygons.
Key words: high-speed EUM; high order polygons; wheel-rail rolling contact; uneven wear; explicit finite element
经过多年的持续快速发展,我国高速铁路网已开始向高寒、高海拔、多山川河谷、高地形落差、茂密林地、沙漠等复杂地理区域延伸,高速动车组运行条件越来越呈现出多样性和复杂性的特点。在特定运行环境下,动车组车轮可能会发生凹磨[1]、多边形[2-3]和滚动接触疲劳[3-4]等不同类型损伤,引发蛇行失稳[5]、异常振动噪声、螺栓松脱断裂和附属件振动疲劳等问题,在恶化运行品质的同时,也威胁行车安全。在欧洲,高速动车组曾发生过低阶(1~5阶)车轮多边形,其根本原因是车轮制造过程中存在非圆缺陷[6-8]。2011年,我国首次在高速动车组跟踪测试中发现了高阶(18~23阶,即车轮1周内包含18~23个非均匀磨耗周期)多边形车轮,2015年,高阶多边形车轮呈大幅度增长态势,造成多起轴箱端盖螺栓断裂等故障,引起业界普遍关注,并开展了一系列研究[9-11]。
大量跟踪数据及统计分析显示,高速车轮高阶多边形具有如下主要特征:1) 波长或通过频率相对固定,一般认为其对应系统的某一阶固有模态;2) 传统不落轮镟床及工艺不能有效镟除已存在的车轮多边形,易导致镟后车轮多边形快速复发,二次进刀工艺、保持驱动轮圆度和增加轴箱定位可显著改进镟除效果;3) 轮径因磨耗和镟修而逐渐减小时,车轮多边形发生率会因表面硬度降低(即磨耗速率提升)而明显增加,尤其是动车轮对;4) 保证轮轨黏着的研磨子亦可有效抑制车轮多边形的发生,甚至消除已有车轮多边形;5) 钢轨不平顺、单一交路和恒速运行均能促使车轮多边形快速发展。武广高铁的实践表明,及时镟修、升级镟床、打磨钢轨、换线和变速运行等被动防治措施可有效控制动车组车轮高阶多边形,统计显示故障件数已由最高峰416件/月下降至100件/月以内[12]。
针对高阶多边形车轮动态响应,众多学者已开展了相关研究[13-15],为理解多边形危害和制定合理镟修门槛值等奠定了基础。WU等[2, 7-8]基于模态分析与测量,研究与车轮多边形通过频率吻合的可能固有模态,探索车轮多边形的萌生机理。近年来,基于隐-显式结合建模的三维轮轨瞬态滚动接触有限元模型逐渐发展成熟并得到广泛应用[16-20]。赵鑫等[16-18]开发了三维高速轮轨瞬态滚动滚动接触模型,于时域内模拟直线轨道上轮轨间的瞬态滚动接触行为,可准确求解轮轨间的轮轨力、黏滑分布、蠕滑率等瞬态接触解。寇峻瑜等[19-20]进一步建立可考虑轮轨几何缺陷的三维轮轨瞬态滚动接触模型,系统地研究了高频激励下轮轨间的瞬态响应。
为了进一步拓展该模型,本文作者以我国某型250 km/h级高速动车组车轮上出现的23阶车轮多边形问题[2]为例(多边形周向波长为118 mm左右),建立其自由轮对的三维轮轨滚动接触模型,并利用轮轨瞬态磨耗计算模型[21],于时域内研究多边形车轮与轨道间高频耦合动力作用、瞬态滚滑及所导致的瞬态磨耗行为,分析高阶多边形逐渐成长的瞬态磨耗机理,为研究车轮多边形主动治理措施奠定基础。
1 模型介绍
1.1 模型概况
某250 km/h速度级动车组拖车车轮的实测23阶车轮多边形(轮径为860 mm)如图1所示。
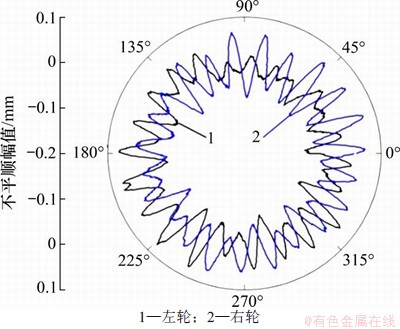
图1 某250 km/h速度级动车组拖车车轮的实测23阶车轮多边形(轮径为860 mm)
Fig. 1 A measured 23-order polygon of trailer wheel of 250 km/h speed class EMU(wheel diameter of 860 mm)
采用ANSYS/LS-DYNA建立的全轮对三维瞬态滚动接触有限元模型图2所示。其主要特点如下:
1) 考虑半径3 500 m的圆曲线段轨道,轨道中心线弧长15.2 m,包含24组间距为0.65 m的扣件,超高为150 mm,轨底坡为1:40。
2) 车轮和钢轨廓形分别取为LMB和CN60,采用相同网格离散左右两侧轮轨,以降低计算误差,最小单元尺寸取1.0 mm(与以往模型保持一致),模型总结点和单元数分别为628.7万个和570.7万个。
3) 拖车车轮多边形是在250 km/h恒速运行中产生的,因此,模拟初速度v设为250 km/h(角速度ω约为161.5 rad/s),轮对初始横移、侧滚角取自动车组稳态曲线通过时的结果[20],轴质量为16 t。
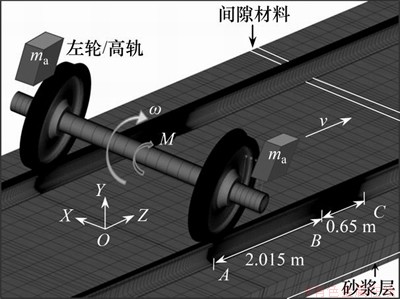
图2 全轮对三维瞬态滚动接触有限元模型
Fig. 2 Three-dimensional transient rolling contact finite element model of full wheel pair
4) 为模拟动车组实际运行中阻力和滚滑行为,在轮对车轴中心施加恒定牵引扭矩M,牵引系数为0.03和0.2对应的M分别为2.02 kN·m和13.48 kN·m;
5) 轮对中3个制动盘的质量(180 kg/个)以等效质量节点的形式加在轮轴轴线的相应位置上。需说明的是,模型未给轮对施加额外运行阻力,因此,模拟中,轮对处于匀加速运动状态,在默认工况下,加速度为0.3 m/s2,因模拟时间很短(仅为0.05 s),其造成的速度变化可以忽略。模型初速度v为250 km/h,摩擦因数f为0.3,牵引系数μ为0.03和0.20,簧上质量为14 441 kg,轮径为860 mm。模型中主要参数如表1所示。
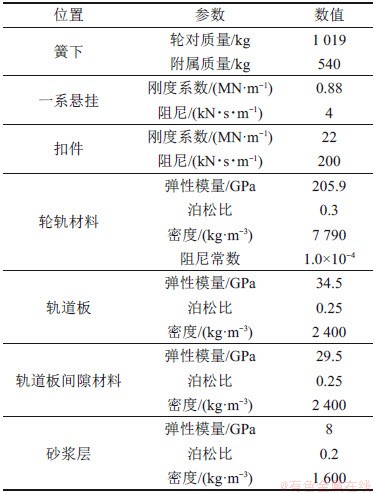
表1 模型中主要参数
Table 1 Main parameters of model
为表述方便,建立图2中所示的笛卡尔坐标系OXYZ,坐标原点位于过两轨底中心线的平面上,X轴方向为横向,Y轴方向为垂向,Z轴方向为纵向。轮对初始位置在A点处,即轨道中心的投影,初始滚动方向与Z轴同向。轨道假设为右曲线,面向运行方向的左侧为左轮/高轨,右侧为右轮/低轨。考虑垂向、横向和纵向轮轨相互作用及其相互耦合关系[16],瞬态分析过程中的边界条件如下:
1) 考虑到两侧簧上质量本为一体,一系悬挂的上、下节点(对应簧上质量与车轴轴心节点)在横向、纵向耦合,保证簧上质量与轮对一起运动;
2) 钢轨、轨道板和砂浆层纵向两端对称约束,以模拟其无限长特性;
3) 钢轨扣件的上、下节点均只保留了垂向自由度;
4) 砂浆层底面全约束。
1.2 多边形施加
网格划分完成后,轮轨表面都是光滑的,采用文献[16]中修改表面相关节点坐标的方法将图1中实测多边形施加于模型中车轮表面。为避免节点修改影响瞬态分析中位移场初始化(对应图2中初始位置A)和动态松弛(对应图2中过渡区AB段)的效果,初始接触斑附近区域未施加几何不平顺,几何不平顺从0°前后施加(起始点从实测的多边形波峰开始)至255°左右结束,如图3所示。横向上,假设多边形深度呈抛物线分布,宽度取50 mm,如图4所示。需说明的是,所施加车轮多边形的相位与图3中测量结果保持一致,初始接触点A处的车轮半径假设为新轮半径0.43 m,多边形区域内的接触半径更小。图5所示为多边形深度扩大50倍后的三维效果图。
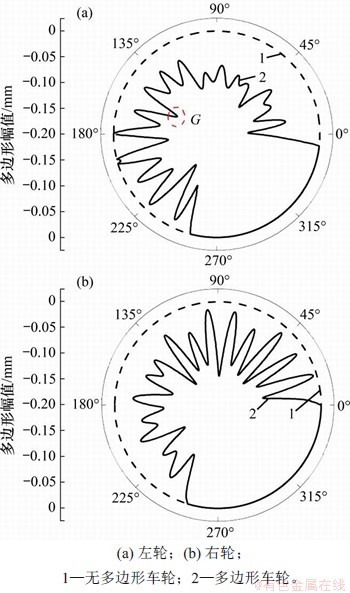
图3 模型中多边形施加后的车轮周向几何不平顺 (车轮半径波动)
Fig. 3 Circumferential geometric unevenness of wheel after application of polygon in model (wheel radius fluctuation)
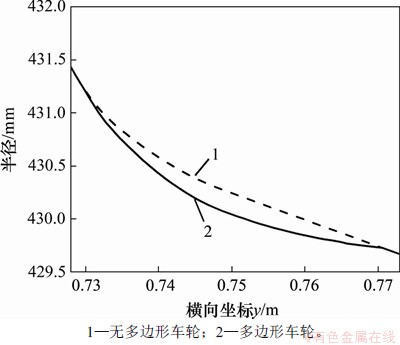
图4 模型中多边形施加后的左侧车轮G点位置(图3(a)中所示)的横向车轮廓形
Fig. 4 Lateral wheel profile of the left wheel G position (shown in Fig.3(a)) applied polygon in model

图5 模型中多边形深度扩大50倍后的车轮外观
Fig. 5 Appearance of wheel after polygon depth expanded by 50 times in model
1.3 磨耗模型
利用上述有限元模型预测轮轨间高速滚滑接触行为,得到表面节点切向力和相对滑移速度随时间的变化及其摩擦功fw时变结果,进一步集成磨耗模型,可计算轮轨表面的瞬态磨耗分布,为研究多边形的发展奠定基础。本文选用Archard磨耗模型[21],任一接触节点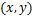 处的磨耗量
处的磨耗量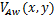 为
为
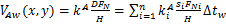 (1)
(1)
式中:D和si分别为节点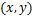 的相对滑移距离(m)和滑移速度(m/s);FN为法向节点力(N);H为维氏硬度,考虑现场实测值,取2.94 GPa;
的相对滑移距离(m)和滑移速度(m/s);FN为法向节点力(N);H为维氏硬度,考虑现场实测值,取2.94 GPa;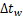 为计算时间步长(s);i为分析时刻;n为总时间步数;
为计算时间步长(s);i为分析时刻;n为总时间步数;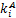 为磨耗系数,
为磨耗系数,
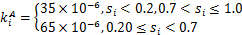 (2)
(2)
假设该节点所代表区域内的磨耗量恒定,则可由磨耗量和该区域面积计算磨耗深度wd。
2 结果分析
考虑到模型计算成本,本文模拟的轮对滚动距离仅2.67 m,假设轮对正在稳态通过半径3 500 m曲线,相应的轮对横移为2.6 mm和侧滚角为0.005 89°以初始条件形式施加,忽略摇头角。因为瞬态滚动接触模型很难达到绝对稳态,平顺轮轨表面条件下也会因连续体振动而存在一定程度的振动,引发非均匀磨耗,所以,本文模拟了2类工况,其中,一类为严格意义上的平顺车轮(无多边形),另一类为有多边形车轮,从而避免平顺工况下结果波动对分析的干扰。另外,为了避免非完美初始条件和多边形进入段引发的复杂瞬态振动行为,分析的重点为初始条件影响已基本消除的后段(图2中B点以后)。
2.1 轮轨力
图6所示为无多边形条件下轮轨力在26~38 ms内的变化,图中,Fx,Fy和Fz分别为横向力、垂向力和纵向力。由图6(a)可见,牵引系数取0.03时,左右两侧的轮轨力均基本进入稳定状态,例如左侧垂向力、横向力和纵向力的波动幅值(峰谷差值)分别为5.5,2.4和2.3 kN,与其静态轮重78.48 kN相比非常小,基本可以忽略。左右两侧的垂向力基本相同,对应着本文所模拟的稳态曲线通过工况;左侧(高轨侧)车轮所受的纵向力向前,右侧向后,产生向右的导向扭矩,使轮对沿右曲线运行;左右两侧横向力方向相反,其合力朝向内轨侧,数值与理论值相符。
由图6(b)可见,在高牵引系数下,轮对也基本进入了稳态滚动状态。由图6(c)可见,增加牵引系数,不影响垂向和横向力,但纵向力的幅值因牵引扭矩的增加而明显提升。另外,在牵引系数为0.03和0.20的工况下,左侧纵向力的波动幅值分别为2.3 kN和5 kN,此波动增大的原因是大牵引扭矩更容易造成轮对的扭转振动。需说明的是,在本文工况中,轮对横移很小,这意味着左右侧的轮轨接触角均很小,垂向轮轨力近似于法向轮轨力;轮轨间蠕滑率很小,所以,轮对滚动距离非常接近其沿钢轨的纵向平移。
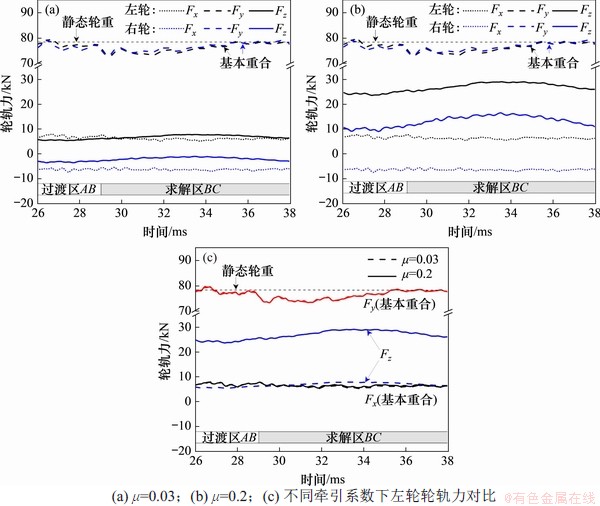
图6 左右两侧轮轨力(无多边形)
Fig. 6 Wheel and rail contact forces of left and right sides(without polygon)
图7所示为牵引系数0.03且存在车轮多边形时左右两侧轮轨力对比,其中滚动距离为时间与滚动速度的乘积。从图7可见,车轮多边形导致了显著的轮轨力波动,对应着车轮多边形的平均通过频率601 Hz,且其走势与多边形幅值波动基本一致,意味着系统在多边形激励下发生了严重的受迫振动。
从图7可知:左、右侧车轮的多边形幅值(峰谷差值)分别为0.128和0.123 mm,而相应的垂向轮轨力最大值分别为113 kN和105 kN,达静态轮重的144%和134%;波动幅值分别为72和52 kN,为静态轮重的91.7%和66.3%。这是现场车轮多边形造成多种损伤和严重后果的主要原因。另外,横向力和纵向力也因车轮多边形的存在而呈现明显的波动,虽然波长特征依然因上述受迫振动而大致相同,但其波动的趋势与垂向力或多边形幅值波动不完全一致。造成这一现象的原因是在滚滑条件下,切向接触在一定程度上独立于法向接触[21]。左侧车轮横向力和纵向力的波动幅值分别为10.5 kN和5.2 kN,右侧车轮横向力和纵向力的波动幅值分别为4.2 kN和4.3 kN。
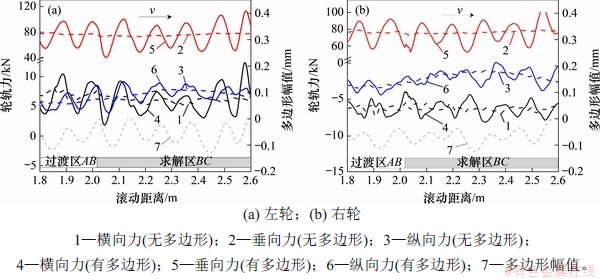
图7 牵引系数为0.03时轮轨力对比
Fig. 7 Comparison of wheel and rail contact forces under a traction coefficient of 0.03
进一步对比轮轨力与多边形幅值波动发现左右两侧的垂向力均存在明显的相位差,且都表现为垂向力波峰超前于多边形幅值波峰出现,这与之前钢轨磨耗的分析结果一致[16-17]。这里“超前”是指轮轨力峰值先于多边形幅值波峰出现,反之,“滞后”是指轮轨力峰值后于多边形幅值波峰出现。横向力和纵向力相对于多边形幅值的相位超前程度均比垂向力的更大,且右侧轮轨力的相位超前程度比左侧轮轨力的大,这是因为左侧(高轨侧)的切向力(见图9)或轮轨间相对滑移更大[21]。
牵引系数为0.03时车轮多边形激励的左右两侧动态轮轨力(有、无多边形工况轮轨力之差)对比如图8所示。从图8可见,每侧的垂向动态轮轨力均只与本侧车轮的多边形相关,与另一侧车轮多边形无关。这是因为当一侧发生的振动传递到另外一侧时已大幅衰减[22],这在一定程度上解释了现场中两侧车轮多边形可以单独发展(有相位差)的原因。总之,虽然一侧车轮多边形所激励的振动可以传递至另一侧,但对另一侧车轮多边形的发展不起主导作用。
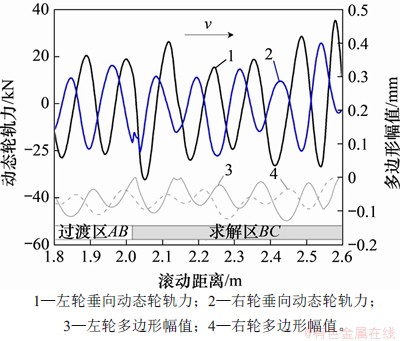
图8 牵引系数为0.03时车轮多边形激励的左右两侧垂向动态轮轨力
Fig. 8 Vertical dynamic wheel and rail contact forces on the left and right sides of wheel excited by polygon under traction coefficient of 0.03
2.2 接触应力及黏滑分布
L1和L2周向路径分别为左、右车轮不同时刻最大法向接触应力发生位置的连线。选取接触斑位于求解区BC内的9个等间隔时刻t1~t9,无多边形车轮在牵引系数0.03下的瞬态法向接触应力p和切向接触应力τ分布如图9所示,图中黑色实心曲线表示法向应力p与摩擦因数f的乘积,即库仑摩擦极限。图中接触斑前沿为黏着区,切向应力小于库仑摩擦极限,后面为滑移区,符合现有理论。可见,各时刻下两侧接触斑内的黏滑和应力分布均无明显变化(最大法、切应力波动幅值均在10 MPa以内),即进一步验证轮对在BC段基本上进入了稳态滚动状态。经对比发现,左、右两侧的最大法向应力差距不大,而相应的最大切向应力则差异明显,分别为180 MPa和58 MPa,即左侧滑移区比右侧滑移区更大。其原因是横移条件下左侧(高轨侧)的纵向轮轨力比右侧的更大(见图6)。
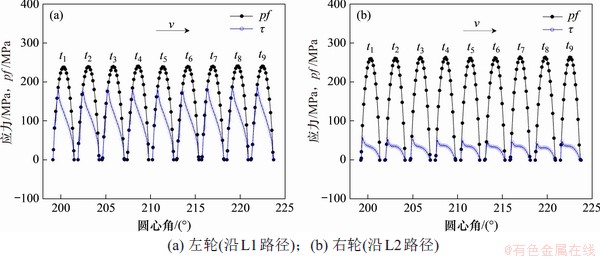
图9 牵引系数为0.03时不同时刻下的瞬态法向应力和切向应力分布(无多边形)
Fig. 9 Distribution of transient normal and tangential stress at different times under traction coefficient of 0.03 (without polygon)
有多边形车轮在牵引系数为0.03下的瞬态法向应力、切向应力分布如图10所示。从图10可见:两侧应力分布因多边形的存在而呈现周期性变化,黏滑分布也相应地波动,例如,左侧最大法向应力、切向应力的波动幅值分别为203 MPa和30 MPa,远大于无多边形车轮工况的波动幅值。此结果与上述轮轨力的波动趋势相对应。
不同牵引系数下最大接触应力沿周向分布(左轮)如图11(a)所示,其中,应力分布曲线的上沿即为L1和L2路径上的最大接触应力分布,pm,τm和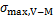 分别为最大法向应力、切向应力和最大V-M等效应力。最大法向应力和切向应力定义为接触区内任一节点整个滚动过程中法向应力、切向应力的最大值,最大V-M等效应力取车轮接触表面的表层单元经历的最大值。从图11(a)可见,无多边形车轮在牵引系数0.03下,左侧法向应力、切向应力的最大值和最大V-M等效应力分别稳定在803,182和410 MPa,对应着稳态滚动。多边形造成的周期性波动,导致法向应力、切向应力和V-M等效应力的最大值分别增至959,214和467 MPa,增幅分别为7%,18%和14%。右侧车轮结果与左侧结果的类似。
分别为最大法向应力、切向应力和最大V-M等效应力。最大法向应力和切向应力定义为接触区内任一节点整个滚动过程中法向应力、切向应力的最大值,最大V-M等效应力取车轮接触表面的表层单元经历的最大值。从图11(a)可见,无多边形车轮在牵引系数0.03下,左侧法向应力、切向应力的最大值和最大V-M等效应力分别稳定在803,182和410 MPa,对应着稳态滚动。多边形造成的周期性波动,导致法向应力、切向应力和V-M等效应力的最大值分别增至959,214和467 MPa,增幅分别为7%,18%和14%。右侧车轮结果与左侧结果的类似。
图11(b)所示为不同牵引系数下的左侧最大应力对比。从图11(b)可见,当牵引系数由0.03增至0.2时,最大法向应力分布基本不变;最大切向应力的最大值和平均值分别由210 MPa和186 MPa增至325 MPa和288 MPa,但波动幅值并无明显变化,由72 MPa增至75 MPa;最大V-M等效应力的最大值和平均值分别由467 MPa和406 MPa增至590 MPa和526 MPa,波动幅值略低(从135 MPa到124 MPa);另外,3类应力相位均随牵引系数无明显变化。
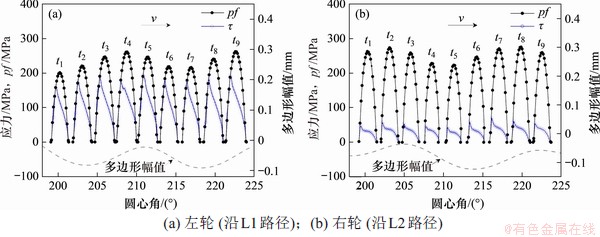
图10 牵引系数为0.03时不同时刻下的瞬态法向应力和切向应力分布(有多边形)
Fig. 10 Distribution of transient normal and tangential stress at different times under traction coefficient of 0.03 (with polygon)
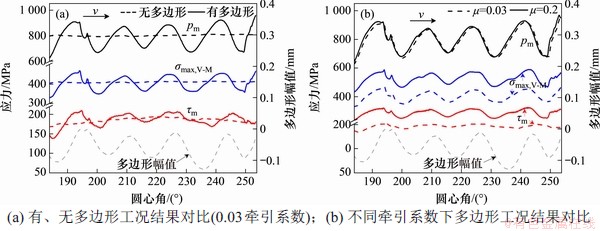
图11 不同牵引系数下最大接触应力沿周向分布(左轮)
Fig. 11 The maximum contact stress distributed along circumference under different traction coefficients (left wheel)
2.3 摩擦功和磨耗
图12所示为有、无多边形车轮在牵引系数0.03下,两侧车轮表面摩擦功沿车轮周向的分布。从图12可以看出,摩擦功也因多边形而呈周期性波动,且其波动与最大切向应力的波动基本一致,这是因为摩擦功取决于蠕滑力和蠕滑率,而在发生全滑之前,二者随牵引系数同向变化。左侧摩擦功在周向范围内的最大值和最小值分别为2.3 mJ和0.8 mJ,即波动幅值为1.5 mJ,右侧摩擦功的最大值和最小值分别为0.25 mJ和0.035 mJ,波动幅值为0.215 mJ,两侧差异源自左侧更大的纵向轮轨力及接触斑内更大的滑移区和更高的切向接触应力。
图13所示为不同牵引系数下摩擦功和磨耗深度的对比。可见,摩擦功和磨耗深度的变化趋势基本同步,这体现磨耗由摩擦导致的物理本质。从图13可以看出,磨耗率峰值发生在多边形幅值波峰附近,其相位在大多数周期内超前于多边形幅值(相位差介于10°~55°之间),少数周期内则稍稍滞后(相位差不超过10°)。磨耗率谷值亦存在相同变化规律。这意味着多边形造成的磨耗波动会抑制多边形进一步发展。本文仅考虑多边形激励下的受迫振动,未考虑到导致多边形萌生的相关振动,因此,上述预测结果可以解释现场中车轮多边形早期快速发展但后期逐渐进入稳定阶段的现象[17]。另外,从图13(a)可见:在牵引系数为0.03时,左侧车轮磨耗深度的最大值和波动幅值分别为34×10-8 mm和22×10-8 mm;当牵引系数增至0.20时,其磨耗深度的最大值和波动幅值分别增至142×10-8 mm和55×10-8 mm。这表明,高牵引系数下车轮的平均磨耗和非均匀磨耗(即多边形)均会较低牵引系数下发展更快。
图12 牵引系数为0.03时两侧摩擦功沿车轮周向分布
Fig. 12 Friction work on both sides distributed along circumferential direction of wheel under a traction coefficient of 0.03
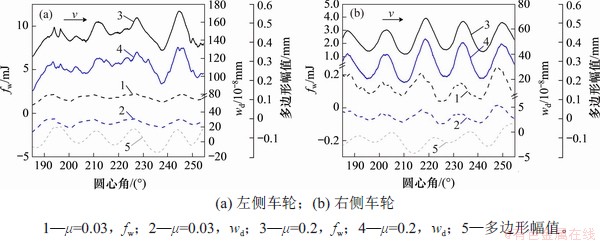
图13 不同牵引系数下左右两侧摩擦功和磨耗深度沿车轮周向的变化
Fig. 13 Variations of friction work and abrasion depth on the left and right sides along circumferential direction of wheel under different traction coefficients
如上所述,本文仅考虑了多边形所激励的振动,未将导致多边形从平顺初始表面萌生的系统振动考虑在内,即本文未研究车轮多边形的萌生过程。本文模拟了轮对单次滚动工况,并基于其结果展开了相应的分析,但未将2次或多次滚动行为之间的相互影响考虑在内;未将现场中经常存在的短距离低黏着区及其所导致的大蠕滑或全滑行为考虑在内;忽略了滚动速度的变化、轮轨材料弹塑性和表面随机粗糙度等因素。未来研究中应该持续完善上述模型,系统研究各因素对车轮多边形萌生与发展的影响,揭示其产生的磨耗机理。
3 结论
1) 所建立的全轮对有限元模型可精确模拟自由轮对在不同横移和侧滚角下高速曲线通过和瞬态滚滑行为,所得到的三向轮轨力、黏滑分布及法/切向接触应力等均合理可靠。
2) 车轮多边形的存在会激励轮轨系统,造成两侧轮轨力、法/切向接触应力、摩擦功及磨耗深度等结果的周期性波动。在峰谷幅值0.128 mm和0.03牵引系数下,最大垂向轮轨力可达113 kN(静态轮重的144%),相应最大波动幅值可达72 kN(静态轮重的91.7%),摩擦功最大值可由平顺表面下的2 mJ增至2.3 mJ,相应波动幅值可达1.4 mJ。在大部分周期内,上述结果周期性波动的相位均超前于多边形的几何波动。
3) 虽然一侧车轮多边形所激励的振动可以通过轮对传至另外一侧,但对车轮多边形发展起主导性作用的仍然是本侧的轮轨动力行为。这可以在一定程度上解释现场中两侧车轮多边形以不同相位单独发展的原因。
4) 车轮多边形存在时,磨耗会出现波动,且磨耗率峰值、谷值分别发生在多边形幅值的波峰、波谷附近,其相位在大多数周期内超前于多边形幅值,少数周期内则稍稍滞后,使得多边形的进一步发展受到抑制。
5) 牵引系数增大,在相同振动条件下,车轮表面的平均磨耗和非均匀磨耗速率波动幅值均会增加,加速车轮多边形的发展。
参考文献:
[1] 金学松, 赵国堂, 梁树林, 等. 高速铁路轮轨磨损特征、机理、影响和对策: 车轮踏面横向磨耗[J]. 机械工程学报, 2018, 54(4): 3-13.
JIN Xuesong, ZHAO Guotang, LIANG Shulin, et al. Characteristics, mechanisms, influences and counter measures of high speed wheel/rail wear: transverse wear of wheel tread[J]. Journal of Mechanical Engineering, 2018, 54(4): 3-13.
[2] WU Yue, DU Xing, ZHANG Heji, et al. Experimental analysis of the mechanism of high-order polygonal wear of wheels of a high-speed train[J]. Journal of Zhejiang University: Science A, 2017, 18(8): 579-592.
[3] 金学松, 温泽峰, 张卫华, 等. 世界铁路发展状况及其关键力学问题全国结构工程学术会议特邀报告[J]. 工程力学, 2004, 21(S1): 90-104.
JIN Xuesong, WEN Zefeng, ZHANG Weihua, et al. Development status of world railway and its key mechanics problem[J]. Engineering Mechanics, 2004, 21(S1): 90-104.
[4] 王文健, 刘启跃. 轮轨滚动接触疲劳与磨损耦合关系及预防措施研究[J]. 中国铁道科学, 2009, 30(4): 137-139.
WANG Wenjian, LIU Qiyue. Study on the coupling relationship between the rolling contact fatigue and the wear of wheel-rail and prevention measures[J]. China Railway Science, 2009, 30(4): 137-139.
[5] 谢清林, 陶功权, 王鹏, 等. 高寒动车组车轮磨耗演变特性及其影响分析[J]. 工程力学, 2019, 36(10): 229-237.
XIE Qinglin, TAO Gongquan, WANG Peng, et al. Wheel wear evolution characteristics of alpine high-speed EMU and analysis of its influence[J]. Engineering Mechanics, 2019, 36(10): 229-237.
[6] MEINKE P, MEINKE S. Polygonalization of wheel treads caused by static and dynamic imbalances[J]. Journal of Sound and Vibration, 1999, 227(5): 979-986.
[7] MORYS B. Enlargement of out-of-round wheel profiles on high speed trains[J]. Journal of Sound and Vibration, 1999, 227(5): 965-978.
[8] NIELSEN J C O, JOHANSSON A. Out-of-round railway wheels-a literature survey[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2000, 214(2): 79-91.
[9] 崔大宾, 梁树林, 宋春元, 等. 高速车轮非圆化现象及其对轮轨行为的影响[J]. 机械工程学报, 2013, 49(18): 8-16.
CUI Dabin, LIANG Shulin, SONG Chunyuan, et al. Out of round high-speed wheel and its influence on wheel/rail behavior[J]. Journal of Mechanical Engineering, 2013, 49(18): 8-16.
[10] 宋春元, 沈文林, 李晓峰, 等. 高速动车组车轮多边形影响因素及抑制措施研究[J]. 中国铁路, 2017(11): 33-40.
SONG Chunyuan, SHEN Wenlin, LI Xiaofeng, et al. On the influencing factors and inhibiting measures of wheel polygons of high-speed EMUs[J]. China Railway, 2017(11): 33-40.
[11] 周易. 新HXD1型机车走行部异常振动分析与对策[J]. 电力机车与城轨车辆, 2018, 41(4): 90-92.
ZHOU Yi. Analysis and countermeasures for abnormal vibration of running gear of new HX_D1 locomotive[J]. Electric Locomotives & Mass Transit Vehicles, 2018, 41(4): 90-92.
[12] 钱卿. 武广高铁车轮多边形综合整治研究[J]. 铁道机车车辆, 2019, 39(2): 50-54.
QIAN Qing. Study on wheel polygon comprehensive improvement of Wuguang high-speed line[J]. Railway Locomotive & Car, 2019, 39(2): 50-54.
[13] 胡晓依, 侯银庆, 宋志坤, 等. 基于柔性轮轨模型的车轮谐波磨耗对高速轮轨系统振动影响的仿真研究[J]. 中国铁道科学, 2018, 39(6): 81-89.
HU Xiaoyi, HOU Yinqing, SONG Zhikun, et al. Simulation study on influence of harmonic wear of wheel on vibration of high-speed wheel-rail system based on flexible wheel-rail model[J]. China Railway Science, 2018, 39(6): 81-89.
[14] 吴越, 韩健, 刘佳, 等. 高速列车车轮多边形磨耗对轮轨力和转向架振动行为的影响[J]. 机械工程学报, 2018, 54(4): 37-46.
WU Yue, HAN Jian, LIU Jia, et al. Effect of high-speed train polygonal wheels on wheel/rail contact force and bogie vibration[J]. Journal of Mechanical Engineering, 2018, 54(4): 37-46.
[15] 尹振坤, 吴越, 韩健. 高速列车车轮多边形磨耗对轮轨垂向力的影响[J]. 铁道学报, 2017, 39(10): 26-32.
YIN Zhenkun, WU Yue, HAN Jian. Effect of polygonal wear of high-speed train wheels on vertical force between wheel and rail[J]. Journal of the China Railway Society, 2017, 39(10): 26-32.
[16] 赵鑫, 温泽峰, 王衡禹,等. 三维高速轮轨瞬态滚动接触有限元模型及其应用[J]. 机械工程学报, 2013, 49(18): 1-7.
ZHAO Xin, WEN Zefeng, WANG Hengyu, et al. 3D transient finite element model for high-speed wheel-rail rolling contact and its application[J]. Journal of Mechanical Engineering, 2013, 49(18): 1-7.
[17] ZHAO Xin, WEN Zefeng, WANG Hengyu, et al. Modeling of high-speed wheel-rail rolling contact on a corrugated rail and corrugation development[J]. Journal of Zhejiang University: SCIENCE A, 2014, 15(12): 946-963.
[18] ZHAO Xin, WEN Zefeng, ZHU Minhao, et al. A study on high-speed rolling contact between a wheel and a contaminated rail[J]. Vehicle System Dynamics, 2014, 52(10): 1270-1287.
[19] 寇峻瑜. 基于显式有限元法的高速车轮多边形动态响应分析[D]. 成都: 西南交通大学牵引动力国家重点实验室, 2018: 1-2.
KOU Junyu. Analyses on dynamic responses of polygonized wheel of high-speed train using explicit FE method[D]. Chengdu: Southwest Jiaotong University, State Key Laboratory of Traction Power, 2018: 1-2.
[20] 许黎明, 刘超, 赵鑫, 等. 全轮对曲线通过时的瞬态滚动接触行为模拟研究[J]. 工程力学, 2019, 36(11): 203-211.
XU Liming, LIU Chao, ZHAO Xin, et al. Analyses of transient wheel-rail rolling contact behavior during curving[J]. Engineering Mechanics, 2019, 36(11): 203-211.
[21] ZHAO Xin, ZHANG Peng, WEN Zefeng. On the coupling of the vertical, lateral and longitudinal wheel-rail interactions at high frequencies and the resulting irregular wear[J]. Wear, 2019, 430/431: 317-326.
[22] 刘超, 赵鑫, 赵小罡, 等. 单侧钢轨波磨对两侧轮轨瞬态响应的影响分析[J]. 机械工程学报, 2017, 53(22): 117-124.
LIU Chao, ZHAO Xin, ZHAO Xiaogang, et al. Analyses of transient wheel-rail interactions excited by unilateral rail corrugation[J]. Journal of Mechanical Engineering, 2017, 53(22): 117-124.
(编辑 赵俊)
收稿日期: 2020 -03 -07; 修回日期: 2020 -05 -10
基金项目(Foundation item):国家自然科学基金高铁联合基金资助项目(U1734201);国家自然科学基金资助项目(51675444);牵引动力国家重点实验室自主研究课题(2019TPL_T17) (Projects(U1734201) supported by the National Natural Science Foundation of China and High-speed Railway Company of China; Project(51675444) supported by the National Natural Science Foundation of China; Project(2019TPL_T17) supported by the Autonomous Research Program State Key Laboratory of Traction Power)
通信作者:赵鑫,博士,副研究员,从事滚动接触疲劳损伤研究;E-mail: xinzhao@swjtu.edu.cn
引用格式: 黄双超, 赵鑫, 张笃超, 等. 高阶多边形车轮的瞬态磨耗行为分析[J]. 中南大学学报(自然科学版), 2021, 52(2): 648-658.
Citation: HUANG Shuangchao, ZHAO Xin, ZHANG Duchao, et al. Analysis on transient wear of high-order polygonal wheels[J]. Journal of Central South University(Science and Technology), 2021, 52(2): 648-658.