基于综合建模方法的铅锌烧结块成分预测
王雅琳1,桂卫华1,阳春华1,陈晓方1,张传福2
(1.中南大学 信息科学与工程学院,湖南 长沙,410083;
2.中南大学 冶金科学与工程学院,湖南 长沙,410083)
摘要: 针对铅锌烧结过程异常复杂的实际情况,提出了一种既可保证预测精度又满足配料计算对数据完备性要求的铅锌烧结块成分预测智能集成模型。该模型综合了机理与多种智能建模方法的优点,对于正常生产情况(即数据完备区),通过模糊分类/组合以及神经网络NN分段描述方法建立了成分预测的监督式分布神经网络模型;对于异常或不常用工况(即数据不完备区),通过专家经验规则修正部分假定或统计参数方式建立经验机理模型;采用串、并联形式将2种模型有机结合,并通过专家推理进行集成协调与更新修正,形成智能集成模型,实现成分可靠、准确的在线预测。在实际生产中运用该模型,烧结块铅、锌成分预测的相对误差分别为1.51%和0.41%。
关键词: 铅锌烧结; 成分预测; 经验机理模型; 监督式分布神经网络; 智能集成模型
中图分类号:TP273 文献标识码:A 文章编号: 1672-7207(2005)01-0113-06
Prediction for Composition of Pb-Zn
Agglomerate Based on Integrated Modeling
WANG Ya-lin1,GUI Wei-hua1,YANG Chun-hua1,CHEN Xiao-fang1,ZHANG Chuan-fu2
(1.School of Information Science and Engineering, Central South University , Changsha 410083, China;
2.School of Metallurgical Science and Engineering, Central South University, Changsha 410083, China)
Abstract: Considering the complexity in Pb-Zn sintering process, an intelligent integrated modeling is presented to assure the composition prediction precision of Pb-Zn agglomerate and to meet the requirements of the data completeness by blending computation, which synthesizes the advantages of mechanism modeling and other intelligent methods. Firstly, under normal production conditions(or on the complete data section), a supervised distributed neural networks(SDNN) is established by fuzzy classification/combination and the description method of different neural networks(NN) on different subspace; then, under abnormal/unusual production conditions(or on the incomplete data section), an expertise and mechanism based(EM) model is built, in which some hypothetical or statistical parameters are modified by empirical rules; lastly, the EM model and the SDNN are integrated in series and parallel structure, and the integrated model is coordinated and updated by use of expert reasoning to realize the on-line prediction of composition. The intelligent integrated model is applied to industrial process, and the relative errors of prediction for lead and zinc are 1.51% and 0.41%, respectively.
Key words: Pb-Zn sintering; prediction of composition; expertise and mechanism based model; supervised distributed neural networks; intelligent integrated model
密闭鼓风炉铅锌烧结过程通过鼓风高温烧结,使铅锌精矿氧化脱硫并固结成块,为鼓风熔炼提供原料。该过程的物理、化学反应极为复杂,固、液、气三相共存,具有明显的非线性、强耦合和大滞后性,过程影响因素多而可测量信息有限,对烧结块成分进行预测非常困难。采用一种有效的方法建立模型实时预测烧结块铅、锌成分,对指导烧结配料计算、控制烧结块成分和稳定熔炼生产都有着非常重要的意义。
目前,用于冶炼过程质量预测的方法主要是机理建模和神经网络[1,2]。机理模型在一定程度上可反映生产状况,但往往依赖对过程机理的掌握程度,建模难度大;有时为了简化,模型包含大量假设与统计信息,精度不高。神经网络NN可任意逼近非线性[3,4],但建模依据测量数据,缺乏物理基础,对于生产数据不完备的情况,所得模型有时与实际系统的规律相矛盾。基于铅锌烧结过程复杂性、成分预测模型精度以及配料计算对数据完备性要求,机理和NN的烧结块成分预测模型都难以满足要求。近几年,许多学者将机理和神经网络方法相结合,有的把机理模型作为NN模型学习数据的依据[5],有的用神经网络取代机理模型中的部分变化参数或难以描述的非线性部分[6-9],有的用神经网络去补偿机理模型的预测误差[10],有的引入专家经验规则[9,11],用组合的方法用于工业生产对象的建模[5-11]。将机理建模与智能方法相结合的综合建模方法成为当前解决复杂生产过程模型化问题的关键手段之一。基于智能集成的思路,作者提出了一种可用于配料优化计算的铅锌烧结块成分预测模型,综合经验机理建模与NN、模糊分类以及专家推理等智能方法的优势,对于正常生产情况(即数据完备区)和异常或不常用工况(即数据不完备区)分别采用多种智能建模方法,并最终将不同数据区的模型集成,实现成分可靠、准确的全局在线预测。
1 铅锌烧结块成分经验机理模型
铅锌烧结过程将干燥的铅锌精矿与烧结机返粉按配比混合制粒成混合料,在烧结机中烧结成满足熔炼要求的烧结块,并为硫酸系统提供SO2浓度符合要求的烟气,其主要化学反应如下。
锌的脱硫反应:
2ZnS+3O2=2ZnO+2SO2↑
铅的脱硫反应:
2PbS+3O2=2PbO+2SO2↑
铁的氧化反应:
2FeS2+5O2=2FeO+4SO2↑
4FeS2+11O2=2Fe2O3+8SO2↑
依据物料平衡中化学反应物与生成物间各元素质量平衡原理以及烧结块和返粉中铅、锌成分较接近的实际情况,烧结块铅、锌成分的关系表达式为:
式中:w(Pb)S和w(Zn)S分别表示烧结块中铅和锌的质量分数;w(Pb)M和w(Zn)M分别表示混合料中铅和锌的质量分数;w(Pb)L和w(Zn)L分别表示烧结过程中铅和锌成分损失;Δw(Pb)和Δw(Zn)分别表示返粉与烧结块铅、锌成分间的差值;RS为结块率,即烧结块与烧结混合料质量的比值;RL为烧损率,即烧结过程中物料的质量损失与烧结混合料质量的比值。在实际生产中,w(Pb)M和w(Zn)M已知;Δw(Pb),Δw(Zn)和RL变化不大,一般用常数表示;w(Pb)L,w(Zn)L和RS与生产操作条件关系密切。为便于短期预测,引入鼓风烧结的专家经验(见表1),对式(1)中参数w(Pb)L,w(Zn)L和RS在线修正。具体实现如下。
a. 取一段历史时期内w(Pb)M,w(Zn)M,w(S)M,v和t的统计值作为基准值,并定义为w(Pb)0M,w(Zn)0M,w(S)0M,v0和t0;根据专家经验和物料平衡计算,设定w(Pb)L,w(Zn)L和RS的初始值为w(Pb)0L,w(Zn)0L和R0S,其中高温和低温烧结2种状态下各有一组基准初始值,w(S)M为混合料中硫的质量分数,v为台车速度,t为床层温度。
b. 根据当前的w(Pb)kM,w(Zn)kM,w(S)kM,vk和tk,按表1的规则求得w(Pb)kL,w(Zn)kL和RkS。
以RkS的计算为例,已知
RkS=(1+α)R0S。(2)
若满足规则R1,则选择高温基准初始值,如R0S=R0S,h;
若满足规则R2,则选择低温基准初始值,如R0S=R0S,l;
若满足规则R3或R4,有
若满足规则R7或R8,有
若满足规则R9或R10,有
αv=-kv×sign(vk-v0)×abs(vk-v0)/v0;
若满足规则R11或R13,有
αt=-kt×abs(tk-t0h)/t0h;
若满足规则R14,有
αt=-kt×abs(tk-t0l)/t0l。
综合以上规则,有
α=(αPb+αS+αv+αt)/4。(3)
式中:α,αPb,αS,αv和αt为修正率;kPb,kS,kv和kt为修正比例系数,一般在(0, 1)之间取值;sign( )为符号函数;abs( )为取绝对值函数;下标h表示高温烧结状态;下标l表示低温烧结状态。
表 1 与烧结过程物料平衡计算有关的经验规则表
Table 1 Expertise rules related to material
equilibrium of sinter process
同理可得w(Pb)kL和w(Zn)kL。
c. 将当前的w(Pb)kM和w(Zn)kM与求得的w(Pb)kL,w(Zn)kL和RkS代入式(1),得到烧结块铅、锌成分预测的经验机理模型:
式中:RL为用一段历史时期内统计的计算值,该值通常不变。
经验机理模型(EM)基于机理分析和专家经验,考虑了大量的过程内部信息,能在一定程度上反映生产状况,尤其是在异常工况、突变工况下,具有一定的灵敏度和鲁棒性;但模型中包含有不少假设条件、统计数据及经验设定,故其预测精度不高。
2 监督式分布神经网络模型
神经网络NN可任意逼近非线性,但实际铅锌烧结过程异常复杂,工况波动频繁,而可测信息有限且相互干扰严重,单一的NN模型往往规模庞大,运算速度慢,易产生过拟合现象,难以得到理想的结果。王旭东等提出的分布式神经网络,按照某种标准将输入样本空间分为具有不同特征值的多个子空间,用不同NN分别描述来解决类似问题[12]。由于样本空间划分只考虑输入变量,无法全面反映生产过程,尤其是铅锌烧结过程输入变量有限,而输出变量是烧结的结果,包括大量过程信息。为此,借鉴文献[13,14]中的方法求取RBF网络隐节点中心的监督式算法,提出了一种监督式分布神经网络模型。
监督式分布神经网络SDNN模型采用多输入单输出结构,出于配料优化计算考虑,通过机理分析和数据相关性分析,输入变量x(k)选取v,w(Pb)M,w(Zn)M和w(S)M,输出变量y(k)分别为w(Pb)S和w(Zn)S。模型采用监督式聚类方法将学习样本集{x(k), y(k)|k=1,2,…}分成q个子空间,然后分别用不同NN进行学习,并采用模糊分类器将各子网综合输出。
监督式聚类方法与文献[15]中的方法类似,不同之处在于:一是将样本期望输出y(k)加到输入x(k)中组成增广输入量[AKx~D](k),即
使无监督聚类变为有监督聚类;二是聚类中心个数与初始位置采用Subtractive clustering方法一次性确定,无须人工设定[16]。式(5)中β为控制y(k)对聚类结果影响程度的参数。
通过监督式聚类可获得q个聚类中心ci(i=1,2,…,q)以及相应的半径ri(i=1,2,…,q)和样本数ni(i=1,2,…,q)。依据q个子样本集{xi(k), yi(k)|i=1,2,…,q; k=1,2,…,ni},可分别采用不同的NN建立子模型,
yi=fNNi(x)。(6)
用模糊分类器将各子模型综合,得到SDNN模型的输出为:
式中:[AKx~D]为模型输入输出按式(5)组成的增广输入,μi为每个类的隶属函数。
用预处理后的1000组烧结生产历史数据,其中640组用于模型学习和训练(β=1),另外360组用于预测,建立烧结块铅、锌成分预测模型(SDNN_Pb和SDNN_Zn),得到模型SDNN_Pb和SDNN_Zn都由3个结构为BP4-15-1的NN子模型组成,按式(7)将3个子网综合起来预测。定义相对预测均方差σ为
则模型SDNN_Pb的σ为3.21%,模型SDNN_Zn的σ为2.37%。SDNN模型具有较高预测精度,但精度受建模数据的完备性影响;另外,监督式聚类中用到待预测的输出变量,SDNN不宜单独使用。
3 成分预测智能集成模型
SDNN模型具有较高预测精度,但模型监督聚类时,用到了待预测的输出变量烧结块成分,模型预测无法直接进行。经验机理模型由于包含不少假设条件、统计数据和经验设定,预测精度不高,但毕竟是对冶金机理和长期生产的专家经验的总结,在一定程度上是可行的,尤其是在异常工况、突变工况下,具有一定的灵敏度和鲁棒性。为此,提出烧结块成分智能集成模型(如图1所示),综合了以上2种模型的优点。
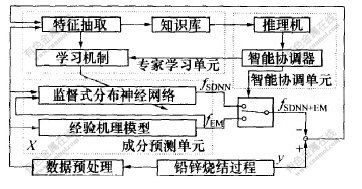
图 1 烧结块成分智能集成模型
Fig. 1 Intelligent integrated model of
agglomerate′s composition
模型由成分预测、智能协调和专家学习3部分组成。成分预测由SDNN模型和经验机理(EM)模型串、并联组成。其中:EM模型的输出引到SDNN模型的输入参加监督式聚类;智能协调单元根据样本数据所处SDNN中的不同子网空间和预测误差情况,协调SDNN模型和EM模型的输出,并决定SDNN模型何时进入学习状态以及采用何种学习机制;专家学习单元实时监督和评价智能协调单元的工作,并有效地充实和修改智能协调规则以及成分预测中的2个模型;NN学习机制为SDNN模型提供多种学习方案,由智能协调器启动,运作中不断与参数库交换数据;集成模型不仅集成了2种模型的优点,且通过在线更新和修正,可不断完善并进一步提高预测精度。
3.1 智能协调单元
智能协调单元包括参数库、推理机和智能协调器3部分。参数库包括智能协调单元在推理过程中所用到的所有参数,有初始参数、中间结果和当前值;推理机完成协调规则的推理工作,而智能协调器则控制输出转换开关和NN学习机制动作。智能集成模型的协调规则有:
模型预测,EM模型仅作为SDNN的输入};
模型预测,协调器启动NN学习机制采用第1种方法修正SDNN模型};
模型预测,协调器启动NN学习机制采用第2种方法修正SDNN模型};
模型预测,协调器启动NN学习机制采用第3种方法修正SDNN模型};
模型预测,SDNN模型不学习, nj=nj+1, 且Dj(k)={Dj(k-1), (x(k), y(k))} };
模型预测,SDNN模型不学习, 新开一个类,即N=N+1, 且nN=1,DN(k)={(x(k), y(k))} };
R7:IF {nj=nmax,j>q} THEN {q=q+1, 第j类与第q类进行交换};
R8:IF {nj=nmin,j>p} THEN {初始化一个BP网络,网络定义3层,隐节点取15个,网络参数随机选取,用样本集Dj训练网络,训练完毕后取消Dj};
R9:IF {rj(k)>rmax} THEN {rj(k)=rmax}。
其中:emin为最小误差阈值;rmax为子类允许的最大半径;Dj为第j类的样本集;N为监督聚类的子类个数,1~q类组成用于预测的SDNN中子模型,其样本个数nj≥nmax,q+1~p类组成正在训练但不用于预测的SDNN子网,其样本个数nmax>nj≥nmin,p+1~N类仅为一些数据样本子集,尚未组成网络,其样本个数nj〈nmin。在烧结块铅、锌成分预测中,定义emin=0.5%,rmax=3.50,nmax=100,nmin=50;对于铅、锌2个集成模型,初始q=3,N=3。
3.2 NN学习机制
NN学习机制为SDNN模型提供多种学习方案,由智能协调器启动,运作中不断与参数库交换数据。NN学习机制主要包括以下3种网络学习方案。
a.方案1。根据预测误差自适应修正SDNN模型中1~q类可预测子网的网络参数,对于实际样本{x, y},若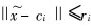
,则用加动量项的变学习率BP算法更新第i个子网。
b.方案2。用于修正SDNN模型中1~q类可预测子网所能描述的样本空间半径。修正过程不改变每个类的中心,仅自适应调整半径。若协调规则R3成立,则定义ri′(0)=ri(i=1,2,…,q),
ri′(k)=ri′(k-1)+γri。(9)
其中: i=1,2,…,q。不断调整ri′(k),直到存在
(k),然后定义nj=nj+1,ri=ri′(k)(i=1,2,…,q)。γ为常数,这里取γ=0.02。
c.方案3。用于更新SDNN模型中第q+1~p个正在训练但不用于预测的子网。具体来说,若第i个子网满足协调规则R4,则有
并用加动量项的变学习率BP算法更新第i个子网的权值。
4 工业应用
铅锌烧结块成分的智能集成预测模型是针对某铅锌冶炼厂的实际情况设计的。目前,该厂已采用DCS集散控制系统实现了整个生产过程的基础控制,重要的过程数据也基本联入厂里的网络中心,可用Visual Foxpro和Access等数据处理软件直接访问。为充分利用厂内有用资源且不影响厂里的正常生产,成分预测以及配料优化计算部分单独用1台PentiumII计算机完成。整个系统的软件用VB 6.0和Matlab 5.2编制。VB主要用于编制用户图形界面,数据访问、管理与打印,以及一些简单的算法。Matlab主要用于编制类似于神经网络的复杂算法。Matlab作为能被VB访问的远程服务器对象,可被VB直接调用。智能集成模型已开始在该厂进行试运行。图2所示为某7d的烧结块铅、锌成分预测结果。图中,实线为实际成分分析值,虚线为模型预测值。烧结块铅、锌成分预测的相对误差分别为1.51%和0.41%。预测结果表明,提出的模型具有较高的预测精度和较强的自学习功能,目前,该模型被用于烧结配料过程专家优化系统中,能满足专家配料优化的需要。
(a)—烧结块铅成分预测结果; (b)—烧结块锌成分预测结果
实线—实际成分分析值; 虚线—模型预测值
图 2 7d烧结块成分预测结果
Fig. 2 Predictive results of agglomerate′s
composition in a week
5 结 论
密闭鼓风炉铅锌烧结过程物理、化学反应极为复杂,具有明显的非线性、强耦合和大滞后。为满足配料计算对预测精度和数据完备性要求,采用机理与智能相结合的综合建模方法,建立了一种铅锌烧结块成分预测的智能集成模型。该模型由监督式分布神经网络(SDNN)模型和经验机理(EM)模型串并联组成,专家协调单元不断更新修正并根据生产的不同情况决定由哪种模型进行成分预测。其中SDNN模型主要用于正常生产情况,确保模型预测精度;EM模型在异常或不常用工况时使用,尽可能保证模型的精度。这2种模型用于实际生产中,烧结块铅、锌成分的相对预测误差分别为1.51%和0.41%,实现了成分可靠、准确的在线预测。
参考文献:
[1]WU Min, NAKANO M, SHE Jin-hua. A Model-based Expert Control Strategy Using Neural Networks for the Coal Blending Process in an Iron and Steel Plant[J]. Expert Systems with Applications,1999,16 (3): 271-281.
[2]WANG Ya-lin, GUI Wei-hua, YANG Chun-hua, et al. Intelligent Modeling and Optimization on Time-sharing Power Dispatching System for Electrolytic Zinc Process[J]. Transactions of Nonferrous Metals Society of China,2000,10(4):561-565.
[3]CYBENKO G. Approximation by Superpositions of a Sigmoidal Function[J]. Mathematics of Control, Signals and Systems, 1989,2(4):303-314.
[4]HORNIK K, STINCHCOMBE M, WHITE H. Multilayer Feedforward Networks Are Universal Approximators[J]. Neural Networks, 1989, 2(5): 359-366.
[5]陈仕学,于乃功,阮晓钢. 基于RBF神经网络的青霉素发酵过程的模型辨识[J]. 中南工业大学学报(自然科学版),2003,34(4):342-344.
CHEN Shi-xue, YU Nai-gong, RUAN Xiao-gang. Model Building in the Penicillin Fermentation Process Based on RBF Neural Networks for Identification[J]. Journal of Central South University of Technology (Natural Science),2003,34(4):342-344.
[6]WILSON J A, ZORZETTO L R M. A Generalized Approach to Process State Estimation Using Hybrid Artificial Neural Network/Mechanistic Models[J]. Comp Chem Eng,1997,21(9):951-963.
[7]HENRIQUES A W S, COSTA A C, ALVES T L M, et al. A Hybrid Neural Model of Ethanol Production by Zymomonas Mobilis[J]. Applied Biochemistry and Biotechnology, 1999,77(9): 277-297.
[8]杨慧中,张素贞,陶振麟. 聚丙烯腈质量指标软测量混合模型的应用[J]. 化工自动化及仪表,2002,29(6):11-13.
YANG Hui-zhong, ZHANG Su-zhen, TAO Zhen-lin. The Application of Soft Measurement Hybrid Model for the Quality Performance of Polyacrylonitrile[J]. Control & Instruments in Chemical Industry,2002,29(6):11-13.
[9]CHEN Xiao-fang, GUI Wei-hua, WANG Ya-lin, et al. Integrated Modeling Method for Prediction of Sulfur Content in Agglomerate[J]. Journal of Central South University of Technology(English Edition),2003,10(2):145-150.
[10]陈晓东,马广富,王子才. 改进的Elman网络与机理模型的互补建模方法[J]. 系统仿真学报,1999,11(2):97-100.
CHEN Xiao-dong, MA Guang-fu, WANG Zi-cai. Mutually Compensatory Modeling Method Based on Mechanism Model and Improved Elman Network[J]. Journal of System Simulation,1999,11(2):97-100.
[11]王亦文,桂卫华,王雅琳. 基于最优组合算法的烧结终点集成预测模型[J]. 中国有色金属学报,2002,12(1):191-195.
WANG Yi-wen, GUI Wei-hua, WANG Ya-lin. Integrated Model for Predicting Burning Through Point of Sintering Process Based on Optimal Combination Algorithm[J]. The Chinese Journal of Nonferrous Metals,2002,12(1):191-195.
[12]王旭东, 邵惠鹤. 基于神经网络的通用软测量技术[J]. 自动化学报,1998,24(5):702-706.
WANG Xu-dong, SHAO Hui-he. The General Soft Sensor Based Neural Networks[J]. Acta Automatica Sinica,1998,24(5):702-706.
[13]PEDRYCZ W. Conditional Fuzzy Clustering in the Design of Radial Basis Function Neural Networks[J]. IEEE Trans on Neural Networks,1998,9(4): 601-612.
[14]CHEN C L, CHEN W C, CHENG F Y. Hybrid Learning Algorithm for Gaussian Potential Function Network[J]. IEE Proceedings-D,1993,140(6): 442-448.
[15]陈建勤, 席裕庚, 张仲俊. 用模糊模型在线辨识非线性系统[J]. 自动化学报,1998,24(1):90-93.
CHEN Jian-qin, XI Yu-geng, ZHANG Zhong-jun. On-line Identification of Nonlinear Systems Using Fuzzy Model [J]. Acta Automatica Sinica,1998,24(1):90-93.
[16]CHIU S. Fuzzy Model Identification Based on Cluster Estimation[J]. Journal of Intelligent & Fuzzy Systems, 1994,2(3): 267-278.
收稿日期:2004-06-06
基金项目:国家重点基础研究发展规划项目(973)(2002CB312203)
作者简介:王雅琳(1973-),女,广东惠州人,副教授,博士,从事复杂过程建模、优化和控制、人工智能以及数据通讯技术等研究
论文联系人: 王雅琳,女,博士;电话:0731-6568649(O);E-mail:ylwang@mail.csu.edu.cn
