文章编号: 1004-0609(2006)09-1500-10

半固态合金流变充型的临界条件

谭建波^{1, 2}, 邢书明¹, 张励忠¹, 李立新², 李增民², 李 讯²

(1. 北京交通大学 机械与电子控制工程学院, 北京 100044;

2. 河北科技大学 材料科学与工程学院, 石家庄 050054)

摘 要: 通过对半固态合金流变充型过程的物理分析, 结合半固态合金包含圣维南体和假塑性体的流变特性, 根据充型驱动力大于或等于充型阻力, 阻流通道内不可流动层厚度小于阻流截面最小厚度的1/2这两个充型临界条件, 运用不可压缩粘性流体流动理论, 建立半固态合金充满型腔获得完整零件的两个临界条件的数学表达式。 为了验证其准确性, 对钩舌、 轴箱体零件进行了流变成形实验, 实验结果证实该临界条件数学表达式的正确性。 该式包含设备参数、 工艺参数、 材料参数和模具参数, 可用来指导半固态流变成形工艺设计、 设备选型, 并能进行缺陷预测和充型过程控制。

关键词: 半固态合金; 充型阻力; 阻流通道; 临界条件 中图分类号: TG421.8

文献标识码: A

Critical condition on rheological filling of semi-solid alloy

TAN Jian-bo^{1, 2}, XING Shu-ming¹, ZHANG Li-zhong¹, LI Li-xin², LI Zeng-min², LI Xun²

(1. School of Mechanical and Electronic Control Engineering, Beijing Jiaotong University, Beijing 100044, China;

2. School of Materials Science and Engineering, Hebei University of Science and Technology,Shijiazhuang 050054, China)

Abstract: By the physical analysis about the rheological filling process of semi-solid alloy, based on the rheological characteristic of semi-solid alloy which includes saint venant body and pseudoplastic, according to the two filling critical conditions that the driving force of mold filling is greater than mold filling resistance and the thickness of non-flowing layer in the channel of resistance to flow is thinner than a half of the minimum of the channel section, managing the flow theory about incompressible viscous fluid, the mathematic representations of the two critical conditions that the cavity can be filled with semi-solid alloy to obtain the perfect casting were deduced. In order to demonstrate the accuracy of the criterion condition, the rheoforming experiment of the hook-head casting and axle box boby casting is carried out. The result of the experiment shows the accuracy of the criterion condition. The mathematic representation includes the equipment parameters, processing parameters, material parameters and mould parameters. It can be used to instruct the technological design and equipment selection about the semi-solid rheoforming. Moreover, it also can be used to forecast flaw and control filling process.

Key words: semi-solid alloy; mold filling resistance; channel of resistance to flow; critical condition

半固态合金流变成形包括浆料制备和成形两部分, 由于其具有成本低、 流程短等优点, 近年来已成为半固态成形技术领域的主攻方向^{[1, 2]}。 邢书明等^[3]利用变直径的多孔模具研究了半固态合金在压力作用下的充型能力, 提出了充型长度的理论计算公式, 为半固态挤压铸造的工艺设计提供了依据。 张海英^[4]就半固态合金熔体充型能力进行了比较系统的研究。 在半固态合金充型过程的研究方面也已取得了较大进展, 张恒华等^[5]和翁文凭^[6]认为内浇道充型速度和内浇道尺寸对压铸件充型过程影响很大。 杨卯生等^[7]和徐宏等^[8]研究表明半固态充型和液态充型具有不同特征, 半固态合金充型具有层流流动特征, 液态合金充型基本呈现紊流特征。 邢书明等^[9]还就白口铸铁磨球半固态挤压铸造的致密化问题进行了实验研究和理论推导, 得到了半固态挤压铸造基本工艺参数的设计计算公式。 张励忠等^[10]提出了钢铁材料半固态流变充型压力、 补缩压力、 加压时间、 收缩率、 锁模力、 压头行程等工艺参数的设计计算公式和原则。

然而, 半固态合金的成形过程是一个包括合金充型、 凝固、 塑性变形的复杂过程, 半固态合金流变充型理论的研究成果目前还较少, 充型过程的工艺设计和控制的基本原则还停留在定性表述的水平上, 至今未见适用于半固态合金流变成形充型工艺准则的报道, 在实验和应用中经常出现冷隔及浇不足等缺陷, 严重影响了半固态合金流变成形技术的推广应用。

本文作者通过对半固态合金流变成形充型机理的理论分析, 提出了半固态合金充满型腔的力学条件和阻流通道畅通条件, 进而得到了半固态合金流变充型临界条件的数学模型。

1 半固态合金流变充型的物理分析

1.1 半固态合金流变充型的本质

由于半固态合金是含有非枝晶初生固相和残余液相的两相共存混合物, 因此, 其充型过程既不同于液态成形的牛顿流体流动过程, 也不同于固态塑性成形中的塑性流动过程, 而是既有粘性又有塑性的非牛顿流体^[11]。 根据流变学理论, 物体内部存在粘性摩擦力, 简称粘滞力。 其大小与切变速率有关, 也与其自身粘度有关。 尽管半固态合金的流变特性很复杂, 还没有公认的统一的流变模型来描述各种半固态合金的流变行为, 但各种流变模型中都至少包括一个临界切应力, 即当外加切应力小于这一临界切应力时, 没有明显的流动, 而当外加切应力大于这一临界切应力时, 才开始流变, 而且持续流变时外加切应力与切变速率呈非线性关系^{[7, 11]}, 表现为假塑性体的流变特征。 为此, 依据半固态合金的流变特性, 其流变模型可以假定为圣维南体τ=τ_c^[11]和假塑性体

因此, 半固态合金流变充型的过程中, 既有圣维南体(临界切应力)产生的流变阻力, 又有假塑性体产生的压强降造成的阻力。

1.2 半固态合金流变充型过程分析

尽管半固态成形方法有多种多样, 但其充型系统一般都包括压室(储料腔)、 直浇道、 横浇道和内浇道4个基本单元。 压室是半固态合金浇入并得以停留的空间, 也称为储料腔; 直浇道是压室中的合金在压力作用下流出压室的通道; 横浇道是连接直浇道和内浇道的过渡通道; 内浇道则是与形成零件的型腔直接相连的通道。 根据半固态合金与压头运动的相对方向, 可以将其流变充型分为反向充型和正向充型两大类。 前者压头运动与压室中的合金运动方向相反, 称为反向充型; 后者压头运动与压室中的合金运动方向相同, 称为正向充型。 反向间接充型示意图如图1所示。 在正向充型和反向充型中压室可兼作直浇道。 对于简单小件, 横浇道和内浇道可以合二为一。

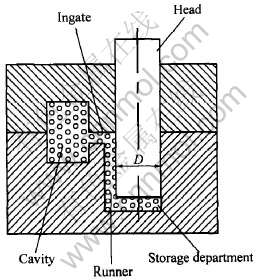
图1  反向间接充型示意图

Fig.1  Schematic of reverse indirect filling

为使建立的模型具有一定的代表性, 在建立模型时采用反向间接充型, 充型系统包括压室(储料腔)、 横浇道和内浇道3个基本单元。 由于充型系统及型腔的形状多为矩形或圆柱形, 本文作者对圆柱形充型系统的圆柱形压室、 矩形横浇道、 内浇道及型腔分别进行了讨论。

半固态合金流变成形过程为: 首先将制备的半固态合金浇入压室, 然后合模、 增压; 接着压头向下移动, 在压头的作用下, 半固态合金沿横浇道和内浇道逐步向型腔充填, 直至充满型腔; 凝固冷却后, 开模、 顶出取件。 在半固态合金浇入压室完毕后到压头施压开始, 其在压室内总要停留一段时间, 这段时间称开始加压时间。 设备精度、 吨位不同, 最短开始加压时间也不同。 由于反向间接充型是在合模、 增压后压头才向下移动, 因此开始加压时间较长, 但一般不大于8s。 由于半固态流变成形的零件尺寸一般比较小, 且充型速度比较快, 半固态合金充满型腔的时间一般为1~2s。

1.3 半固态合金流变充型阻力分析

从流变力学的观点出发, 其充型过程能否顺利进行, 将取决于充型驱动力和充型阻力的相对大小。 如果充型驱动力大于充型阻力, 则充型过程可以顺利进行, 相反, 充型过程就会中止。 下面着重分析充型阻力的种类和来源。

首先, 在半固态合金浇入压室完毕后到压头施压开始这段时间内, 靠近压室内壁会形成一层接近于全固态且能塑性变形的滞留层。 滞留层的变形抗力将减小作用在半固态合金上使其流变充型的有效压力, 因此, 在压头加压前压室内形成的滞留层的变形抗力是充型阻力的重要组成部分。 压头在压下过程中, 由于压室内壁涂有一层涂料, 滞留层变形时与压室内壁的摩擦力较小, 计算时可以忽略滞留层与压室壁摩擦力。 如前分析, 半固态合金流变充型时存在圣维南体和假塑性体产生的阻力, 因此, 其在压室内要开始流变, 还必须克服滞留层内半固态合金的流变阻力。 开始流变后, 在流经压头底部和压室底部两个面时, 也会产生粘滞阻力。 另外, 半固态合金中的假塑性体在流变过程中也会产生压强降, 但由于在压室内开始流变后, 半固态合金高度在不断变化, 且压室的高度也不大, 在后面的计算中忽略了压室中的压强降。

其次, 在半固态合金流变充型的过程中, 假设型壁无滑脱, 粘滞阻力最大的部位为其流经的型壁附近。 当在型壁处受到的剪切应力大于临界流变切应力时才开始流变充型, 考虑到充型路径包括横浇道、 内浇道和型腔, 因此半固态合金流变充型需克服在这3部分中产生的粘滞阻力。 由于其中存在假塑性体, 还需克服假塑性体产生的压强降。 如前所述, 半固态合金充满型腔的时间只有1~2s, 其传热时间很短, 温度变化较小, 在计算横浇道、 内浇道及型腔中半固态合金流动的粘滞阻力时, 可以假定其在充型过程中是等温充型^{[5, 12]}, 即充型过程中临界流变切应力不变。 半固态合金属非牛顿流体, 在通常加工条件下, 粘度比较高, 且充型过程中剪切速率比较高, 故其充型流动可视为层流流动^{[5, 12]}。 因此, 半固态合金的流变充型可视为沿流动方向做稳定等温层流充型。

第三, 可流动的半固态合金前端的自由表面处还会受到表面张力、 型腔气体的压力以及模壁对半固态合金产生的摩擦力。

型腔气体压力产生的充型阻力与充型速度、 型腔的排气能力直接相关。 一般来说, 在模具设计时都采取了必要的措施来强化型腔气体的排除, 所以, 这一阻力很小。 流变充型过程中, 在流道内形成的滞留层也会阻碍充型, 但只要不堵塞流动通道, 则其对流变充型起阻碍作用的只是其与可流变区之间的界面摩擦力, 而不是其本身的变形抗力。 在后面的计算中, 型腔气体的压力以及模壁对半固态合金产生的摩擦力忽略不计。

以上阻力都将阻碍半固态合金的流变充型, 所以把滞留层的变形阻力、 可流动半固态合金粘滞力产生的流变阻力、 半固态合金中假塑性体产生的压强降、 表面张力产生的阻力之和称之为充型阻力。

2 半固态合金流变充型数学分析

2.1 充型阻力的定量计算

2.1.1 压室内充型阻力

1) 滞留层的变形阻力

滞留层的固相体积分数较高, 接近于全固态。 假定滞留层是完全凝固层, 开始加压时间为t_p, 则压头开始加压时, 压室内滞留层的平均厚度δ可以根据平方根定律^[13]估算:

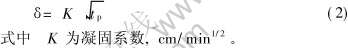
设压室直径为D, 滞留层的塑变抗力为σ_s, 则压头在压下的过程中, 滞留层沿压下方向变形而产生的变形阻力F_b1为

综合式(2)和(3)得

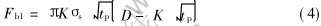
2) 半固态合金的流变阻力

设半固态合金的流变应力为σ₀, 则流变阻力F_b2为

3) 半固态合金的粘滞阻力

设压室的底面积为A_y, 半固态合金开始流变后, 在流经压头底部和压室底部两个面时, 克服临界切应力产生的最小粘滞阻力为

2.1.2 横浇道内充型阻力

1) 粘滞阻力

半固态合金在流经横浇道时, 需克服临界切应力产生的粘滞阻力, 设与流动方向平行的横浇道的侧面积分别为S_h, 则在横浇道中流动必须克服的最小粘滞阻力F_n1为

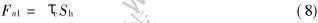
2) 横浇道内的压强降

由于充型系统及型腔的截面形状多为圆柱形或矩形, 因此, 下面的建模主要针对圆柱形或矩形进行。 假设横浇道为圆柱形, 如前所述, 由于可以假定半固态合金的流动为沿流动方向做稳定等温层流, 由假塑性体在圆柱形轴向z流动的状态方程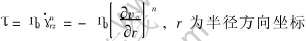, 可得半固态合金中假塑性体在圆柱形浇道中流动时的体积流率方程^[14]

设压头的压下速度即半固态合金在压室内的平均流速为v(称为充型速度), 根据流体的连续性方程, 则半固态合金在横浇道内的平均流速v[TX-]₁=πD²v/πD²₁=D²v/D²₁, D₁为横浇道直径。 L₁为横浇道长度, 由v[TX-]₁=4qv/πD²₁, 可得半固态合金在圆柱形横浇道内流动的压强降:

如果横浇道为矩形, 设横浇道宽为W₁, 高为H₁, 且宽高比W₁/H₁〈10时, 半固态合金中的假塑性体在矩形横浇道流动时的体积流率方程^[14]:

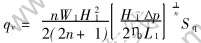
式中 S_q为矩形两侧壁对流率的修正系数。

由v[TX-]₁=[SX(]qv[]W₁H₁[SX)]=[SX(]πR²v[]W₁H₁[SX)], R为压室半径, 可得半固态合金在矩形横浇道内流动的压强降:

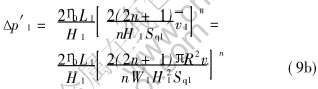
2.1.3 内浇道内充型阻力

设与流动方向平行的内浇道的侧面积分别为S_n, D₂为内浇道直径。 L₂为内浇道长度, 采取与横浇道内充型阻力相似的分析方法, 可得内浇道内最小粘滞阻力F_n2和压强降的表达式:

在圆柱形内浇道中流动的压强降:

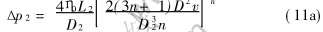
在矩形内浇道中流动的压强降:

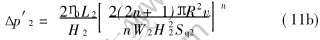
式中 H₂为内浇道高, 内浇道宽为W₂。

2.1.4 型腔内充型阻力

型腔形状千差万别, 但总可以大致区分水平和垂直两个充型流动方向, 于是, 采用类似的方法可以计算型腔内的粘滞阻力和压强降。

1) 型腔内的粘滞阻力

2) 型腔内压强降

如果将型腔也看成是等截面圆管, 半固态合金在型腔流动的压强降Δp₃可以比照式(9)写为

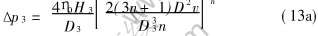
同理, 在等截面矩形型腔中流动的压强降:

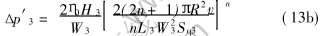
式中 H₃为型腔的高度, L₃为型腔长度, W₃为宽。

综合上述, 半固态合金要充满型腔必须克服的粘滞阻力F_n是流经充型系统和型腔的粘滞阻力之和, 将式(7)、 (8)、 (10)和(12)合并整理得

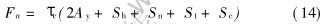
令S=(2Ay+Sh+Sn+St+Sc)称为流变剪切面积, 则粘滞阻力简化为

2.1.5 表面张力引起的阻力

由于半固态合金存在一定的表面张力, 且一般与型壁不完全润湿, 即润湿角大于90°, 故在充型系统或型腔内充型时其液面是凸起的, 而由表面张力产生的一个指向半固态合金内部的附加压力会阻碍流变。 尽管这一阻力在半固态合金流经充型系统和型腔时都起作用, 但它们是循序进行的, 在任意瞬间, 这一阻力只对流头前端起作用, 所以, 这一阻力可以用充型系统以及型腔两者中与流动方向垂直的周长最大的一个计算即可。 设其最大周长l_d, 半固态合金的表面张力σ_LG, 与型壁的润湿角为θ, 则由表面张力引起的充型阻力F_σ为

经计算, 表面张力引起的充型阻力和粘滞力、 流变阻力等相比数值很小[计算过程见附录], 因此可忽略。

综合上述各种充型阻力, 可以得到半固态合金在圆柱形充型系统及圆柱形型腔流变充型的总阻力F为

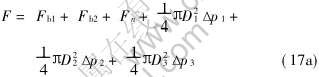
同理可得在圆柱形压室、 矩形充型系统及等截面矩形型腔流变充型的总阻力为

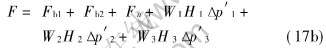
2.2 半固态合金流变充型的力学条件

半固态合金流变充型必须满足充型驱动力大于或等于充型阻力之和。 若用P表示作用在半固态合金上的充型驱动力, 其流变充型力学条件可表示为

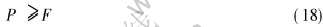
由此可得半固态合金在圆柱形充型系统及圆柱形型腔流变充型的力学条件为

式中 δ′=(D-K[KF(]tp[KF)]), δ″=(D-2K[KF(]tp[KF)]), C是与模具尺寸有关的常数, 其具体表达式为

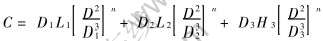
同理, 半固态合金在圆柱形压室、 矩形充型系统及等截面矩形型腔流变充型的力学条件为

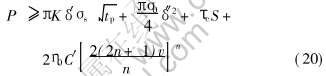
式中 C′是与模具尺寸有关的常数, 其具体表达式为

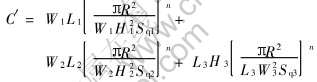
通过计算发现[计算过程见附录], 半固态合金在型腔中流动的压力降与压室、 充型系统及型腔中的总阻力相比小得多, 即使忽略型腔中的压力降, 带来的偏差也较小, 为4%左右。 因此, 对于型腔采用圆管或等截面矩形进行简化处理, 虽然不很精确, 但也不会对充型条件产生大的影响。

如果忽略型腔中的压强降, 式(19b)、 (20)的形式不变, 只不过C、 C′的表达式得到了进一步简化, 即

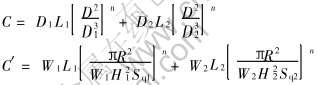
2.3 阻流通道畅通条件

半固态合金要充满型腔, 只满足充型的力学条件是不够的, 还必须保证在充型的整个过程中充型通道始终畅通。

对于不同的零件, 充型通道的形状和结构会存在很大差异, 但总存在某个部位或一段(阻流部位或阻流段)截面较小, 这一部位称为阻流通道。 阻流通道的截面积称为阻流截面。 虽然在前面理论推导中假设半固态合金在模具中充型过程中温度不变, 原因是其充型时间短, 可以认为临界切应力的数值不变, 目的是使模型简化。 但是, 在实际充型过程中半固态合金会产生温度降, 由于阻流通道截面较小, 即使产生较薄的滞留层也会对其充型有较大的影响。 半固态合金的充型本质是流变充型, 只要阻流通道畅通, 不论扩张角是否为零, 充型过程都可以进行。 所以, 充型通道畅通与否取决于阻流通道(阻流段或阻流部位)内的半固态合金是否能够流动, 即阻流通道是否堵塞。

阻流通道堵塞的主要原因是半固态合金在这里产生优先凝固, 并随时间的延长, 滞留层有增厚的趋势。 另一方面, 由于高温半固态合金的流动冲刷和切变, 有可能使滞留层厚度减小。 在其充型的过程中, 如果阻流通道内滞留层的厚度始终小于其截面最小厚度的一半, 则阻流通道就会保持畅通。

假如不考虑流动带来的滞留层厚度减小, 充型过程中阻流通道任一时刻的滞留层厚度δ₁可由平方根定律^[13]计算

根据流体的不可压缩原理和连续性原理, 半固态合金充满充型系统及型腔总容积为V_Q(压室的容积除外)所需的时间t_c2为

高温半固态合金流经阻流通道导致的滞留层减薄作用可以根据传热学进行估算。 其中, 在时间t_c1内通过阻流通道时对流换热释放的热量q₁可由牛顿冷却公式进行计算

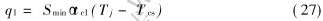
式中 S_min为阻流通道侧面积, α为对流换热系数, T_j为浇注温度, T_cs为不可流动层的温度。

阻流通道中的滞留层在时间t_c1内通过涂料、 金属模具导出的热量q₂可由傅立叶定律进行计算

假设半固态合金通过阻流通道时释放的热量减去阻流通道中滞留层通过涂料层和模具散失的热量差全部由阻流通道内靠近熔体的滞留层吸收, 并且能使其温度提高到T_c1, 由不可流动状态变成了可以流动状态, 即不可流动层减薄了。 设滞留层可减小的厚度为δ₂, 阻流通道截面的周长为l_z, 阻流通道的长度为L, 合金比热容为c, 临界固相分数为f_sc, 液固转变时的摩尔焓变为ΔH_m, ρ为半固态合金的密度, 则这部分滞留层温度由T_s提高到T_cl所需的热量q₃为

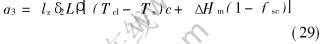
根据热量守恒原理

综合式(27)、 (28)、 (29)及(30)并加以整理得

如果δ₁-δ₂小于阻流通道截面最小壁厚的一半, 则半固态合金充满型腔之前阻流通道始终畅通。 设阻流通道截面最小厚度为b, 半固态合金充满型腔之前阻流通道始终畅通的条件为

3 半固态合金流变充型的临界条件

综合上述分析可见, 半固态合金流变充型的条件有两个: 一是充型驱动力必须大于充型过程的总阻力; 二是充型过程中阻流通道始终畅通。 同时满足这两个条件的充型过程可以保证型腔充满, 只要其中任一条件不满足, 就会导致充型不完整。 因此, 这两个条件就构成了半固态合金流变充型的临界条件。

半固态合金在圆柱形充型系统及圆柱形型腔流变充型临界条件的数学表达式可以根据式(18)和(32)直接写出

4 验证与讨论

4.1 验证

为了验证上述临界条件的有效性和准确性, 对钩舌零件进行了流变成形实验, 钩舌模具的压室为圆柱形, 横浇道、 内浇道为矩形, 型腔可近似为矩形, 阻流通道为内浇道。 材料为A356, 成形设备为合模力2000kN、 充型力630kN、 最大空载速度400mm/s的半固态模锻机。 实验工艺参数为充型速度55mm/s, 半固态合金温度580℃, 模具温度300℃, 开始加压时间8s。 按半固态合金流变充型临界条件公式(35)计算的充型力应为213kN, 阻流截面最小壁厚应大于7.5mm。 用于模型计算的参数数值^{[11, 13-16]}见表1, 用于钩舌计算的参数数值见表2, 实验工艺参数及结果见表3, 图2所示是反向间接成形的钩舌零件。

表1  用于模型计算的参数数值

Table 1  Parameters for calculation of model

表2  用于钩舌计算的参数数值

Table 2   Parameters for calculation of hook-head

 

图2  反向间接成形的钩舌零件

Fig.2  Hook-head casting with reverse indirect forming

表3  钩舌实验条件及结果

Table 3  Testing conditions and results of hook-head

由表3可见, 充型力和阻流截面最小壁厚满足设计要求的方案Ⅰ所得产品轮廓清晰, 而不符合充型临界条件要求的方案Ⅱ(违背力学条件)和方案Ⅲ(违背阻流通道畅通条件)均未充满, 证实了充型条件(35)的可用性。

对轴箱体零件(材料为A356合金)直接挤压流变成形实验也证实了充型临界条件的正确性, 实验条件及结果见表4。 图3所示是反向直接成形的轴箱体零件。

表4  轴箱体实验条件及结果

Table 4   Testing conditions and results of  axle box boby

图3   反向直接成形的轴箱体零件

Fig.3  Axle box body casting with reverse direct forming

4.2 讨论

4.2.1 流变充型临界条件的适用范围

在推导流变充型临界条件的过程中, 始终是针对如图1所示的间接充型进行的, 但这并不说明所得结果只适用于间接充型。 事实上, 对于如图4所示的直接充型, 基本结论是一致的, 只是由于这里没有了横浇道、 内浇道, 压室兼做型腔, 数学表达式可以进行简化。 如式(34a)变为

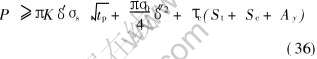
因此, 式(34)、 (35) 涵盖了反向间接成形和直接成形, 具有通用性。

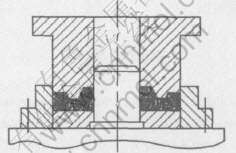
图4  反向直接成形示意图

Fig.4  Schematic of reverse direct forming

类似地, 尽管这里是针对半固态合金浆料成形(也有人称为流变成形)进行的, 但由于坯料成形(也有人称为触变成形)与半固态合金浆料成形的本质都是流变成形, 差别只是坯料在成形前需要加热, 所以, 所得结果对于坯料成形也是适用的。

该临界条件不仅适用于圆柱形充型系统及型腔, 矩形充型系统及型腔, 通过公式的变换也适用于圆柱形、 矩形充型系统, 圆柱形型腔、 矩形型腔的交叉组合。

4.2.2 流变充型临界条件的用途

由式(34)、 (35)可见, 充型临界条件中包括了材料特性(σ_s, σ, T_s, ρ, ΔH_m, f_sc, C, τ_c)、 零件尺寸(V_Q, S_t, S_c)、 冷却条件(λ, T₀, δ_m)、 工艺参数(t_p, T_j)以及设备参数(P, v)等方面, 所以它既是给定条件下流变成形的充型条件, 又可据此进行设备选型、 工艺设计和缺陷预测。

4.2.3 有效性和可靠性

作为一个充型条件需要经过大量的实际应用验证。 尽管这里已经对不同零件、 不同成形方式进行了一些实验验证, 但其广泛适用性、 有效性和可靠性还有待于进一步考查。

5 结论

1) 保证半固态合金充满型腔的充型临界条件包括力学条件和充型通道畅通条件两个方面。 其中力学条件要求充型驱动力大于充型阻力之和, 其数学表达式如式(19)、 (20); 充型通道畅通的条件是阻流通道内的不可流动层厚度小于阻流截面最小厚度的1/2, 其数学表达式如式(33)。 任何一个条件不能满足, 都会出现充型不完整缺陷, 只有两个条件同时满足才能保证充满型腔。

2) 该充型临界条件包括了设备参数、 工艺参数、 材料参数和模具参数, 可以用来指导半固态流变成形工艺设计、 设备选型, 并能进行缺陷预测和充型过程控制。

REFERENCES

[1]Ji S, Fan Z, Bevis M J. Semi-solid processing of engineering alloys by a twin-screw rheomolding process[J]. Mater Sci Eng A, 2001, 299: 210-217.

[2]Yueko J. Idra prince rheocasting and squeeze casting technology[J]. Die Casting Engineer, 2002(4): 20-23.

[3]XING Shu-ming, ZHANG Li-zhong. Mold filling ability of semisolid alloy[J]. Journal of University of Science and Technology Beijing, 2002(3): 253-257.

[4]张海英. 半固态合金充型能力研究[D]. 北京:北京交通大学, 2005. 3.

ZHANG Hai-ying. Mold Filling Ability of Semisolid Alloy[D]. Beijing: Beijing Jiaotong University, 2005. 3.

[5]张恒华, 邵光杰. 复杂零件半固态压铸充型过程的计算机仿真[J]. 铸造, 2003, 52(10): 769-772.

ZHANG Heng-hua, SHAO Guang-jie. Computer simulation of filling complex cavity during semi-solid die casting[J]. Foundry, 2003, 52(10): 769-772.

[6]翁文凭. 镁合金半固态流变压铸充型流动过程分析[J]. 铸造, 2004, 53(11): 894-897.

WENG Wen-ping. Analysis for mold filling process of rheo-die-casting of semi-solid magnesium alloy[J]. Foundry, 2004, 53(11): 894-897.

[7]杨卯生, 徐宏, 毛卫民. 半固态铝合金铸件触变充型过程的模拟[J]. 中国有色金属学报, 2003, 13(1): 36-38.

YANG Mao-sheng, XU Hong, MAO Wei-min. Filling simulation on semi-solid forming for aluminum casting[J]. The Chinese Journal of Nonferrous Metals, 2003, 13(1): 36-38.

[8]徐宏, 杨卯生, 钟雪友. 铝合金半固态触变充型模拟技术研究[J]. 西北工业大学学报, 2004, 22(3): 292-295.

XU Hong, YANG Mao-sheng, ZHONG Xue-you. Simulation study of flow characteristics of semi-solid slurry filling for aluminium alloy[J]. Journal of Northwestern Polytechnical University, 2004, 22(3): 292-295.

[9]邢书明, 张励忠. 白口铸铁磨球半固态挤压铸造工艺参数设计[J]. 铸造, 2002, 51(7): 431-434.

XING Shu-ming, ZHANG Li-zhong. Process parameters design of semi-solid squeeze casting for producing white cast iron milling ball[J]. Foundry, 2002, 51(7): 431-434.

[10]张励忠, 邢书明. 钢铁材料半固态流变成形工艺参数设计原则[A]. 中国压铸、 挤压铸造、 半固态加工学术年会论文集[C]. 深圳: 特种铸造及有色合金, 2003: 291-293.

ZHANG Li-zhong, XING Shu-ming. Process parameters design of semi-solid rheoforming for steel materials[A]. Proceeding of the Die casting, Squeeze Casting and Semi-solid Processing[C]. Shenzhen: Special Casting and Nonferrous Alloys, 2003: 291-293.

[11]林柏年. 铸造流变学[M]. 哈尔滨: 哈尔滨工业大学出版社, 1991.

LIN Bai-nian. Foundry Rheology[M]. Harbin: Harbin Institute of Technology Press, 1991.

[12]崔成林, 毛卫民, 赵爱民. 半固态触变压射成形过程模拟与验证[J]. 北京科技大学学报, 2001, 23(3): 238-240.

CUI Cheng-lin, MAO Wei-min, ZHAO Ai-min. Verification and numerical simulation for semi-solid modeling the thixforming process[J]. Journal of University of Science and Technology Beijing, 2001, 23(3): 238-240.

[13]李庆春. 铸件形成理论基础[M]. 哈尔滨: 哈尔滨工业大学出版社, 1983: 11.

LI Qing-chun. Rationale of Casting Forming[M]. Harbin: Harbin Institute of Technology Press, 1983: 11.

[14]徐佩弦. 高聚物流变学[M]. 北京: 化学工业出版社, 2003: 9.

XU Pei-xuan. Polymer Rheology[M]. Beijing: Chemical Industry Press, 2003: 9.

[15]唐靖林. 半固态A356合金流变行为的研究[D]. 北京: 清华大学, 2000: 4.

TANG Jing-lin. Study on Rheological Behavior of Semi-solid A356 Aluminum Alloys[D]. Beijing: Tsinghua University, 2000: 4.

[16]邢书明. 铝合金半固态连铸技术与理论[D]. 北京: 清华大学, 2001: 6.

XING Shu-ming.The Technology and Theory of the Semi-solid Continuous Casting of Aluminum Alloy[D]. Beijing: Tsinghua University, 2001: 6.

附录

半固态合金在等截面圆柱形充型系统及圆柱形型腔流变充型的力学条件为

基金项目: 河北省教育厅基金资助项目(2003217); 北京交通大学科研基金“十五”重大资助项目(230-12)

收稿日期: 2005-01-24; 修订日期: 2006-06-05

通讯作者: 谭建波, 教授; 电话: 0311-87061863; E-mail: tanjian1998@163.com

(编辑何学锋)