井间视电阻率的几何成像方法

沈平¹，强建科¹，李永军²，阮百尧³

 (1. 中南大学 信息物理工程学院，湖南 长沙，410083；

2. 华北科技学院 安全工程学院，北京，065201；

3. 桂林理工大学 资源与环境系，广西 桂林，541004)

摘  要：基于非全空间直流电场的原理，采用镜像法推导出有别于半空间和全空间的视电阻率计算公式，求出与所有电位对应的视电阻率；以观测井深为纵坐标、供电井深为横坐标绘制视电阻率等值线图，由此得出井间异常体的影像图；应用三维三线性插值有限单元正演模拟方法，计算并分析几种典型的地质模型。研究结果表明：由视电阻率等值线形态能够判断异常体的空间形态和正确位置，但井间低阻体表现为高视电阻率异常，井间高阻体表现为低视电阻率异常；采用该方法所得垂向分辨率较高，确定深度较准确，但不能得出地层真电阻率。

关键词：视电阻率；镜像法；井间成像；几何成像

中图分类号：P631.32          文献标志码：A         文章编号：1672-7207(2010)03-1079-06

Geometry image method of crosshole apparent resistivity

SHEN Ping¹, QIANG Jian-ke¹, LI Yong-jun², RUAN Bai-yao³

 (1. School of Info-physics and Geomatics Engineering, Central South University, Changsha 410083, China;

2. Safety Engineering College, North China Institute of Science and Technology, Beijing 065201, China;

3. Department of Resources & Environmental Engineering, Guilin University of Technology, Guilin 541004, China)

Abstract: Based on the theory of direct-current electric field in non-full space, the apparent resistivity formula that is different from half space and full space was deduced by the image method, and all apparent resistivities were determined, then the apparent resistivity isopleth map was drawn, in which observation hole depth was ordinate and power-supply hole depth was abscissa. At last, several typical geologic models were simulated by three-dimensional finite element method. The results show that the space shape and precise position of abnormity body can be judged from apparent resistivity isoline shape, but crosshole low resistivity body reflects high apparent resistivity abnormity and crosshole high resistivity body reflects low apparent resistivity abnormity. This method has high resolution in perpendicular direction, and can accurately ascertain the depth, but real resistivity of stratum can’t be obtained.

Key words: apparent resistivity; image method; crosshole image; geometry image

早在20世纪80年代末，井间电阻率成像就引起了国外地球物理学家们的极大兴趣。Shima等^[1]在1987年提出了“电阻率层析成像”概念，并研究了成像的可能性和反演算法。之后，Daily等^[2]用拉普拉斯方程的非线性反演方法进行了井间电阻率成像研  究。Shima^[3-4]提出了用有限元法模拟和中心法联合反演来重建地下电阻率分布图像，获得了较好的结果。国内开展这方面的研究工作始于20世纪90年代中后期。周兵等^[5-8]通过求取Jacobi矩阵的格林函数法和平滑度约束反演方法来实现2.5D井间电阻率成像，得到了较好的井间电阻率成像效果。吴小平等^[9-10]将共轭梯度法用于三维电阻率成像，此法在每次反演迭代过程中仅需要1次正演计算，大大提高了计算速度。同时，在反演中将平滑度约束引用到最小二乘准则中，有效地消除了多余构造信息，可得到与实际情况非常接近的、稳定可靠的反演结果。底青云等^[11-14]提出了积分三维反演成像法，此法在计算上优于有限单元法，与共轭梯度法一样快捷，可以方便地进行大电阻率差异背景下的成像。吕玉增等^[15-16]在分析电性不均体对电位影响的基础上，找到了1个直接成像的参数，但该参数的物理概念不是很明确，也没有按照普遍的物理规则来运算。综上所述，现有井间成像方法对异常体的纵向位置定位精度较低，需要进一步研究。

1  几何成像方法

本文提出一种几何成像方法。与传统的井间电阻率成像方法相比，观测方式是一致的，它们都是在一口钻井中布置供电电极A，另一口钻井中布置测量电极M，对供电电极依次供电，观测测量电极的电位，然后，将观测电位换算成视电阻率。其观测系统如图1所示。

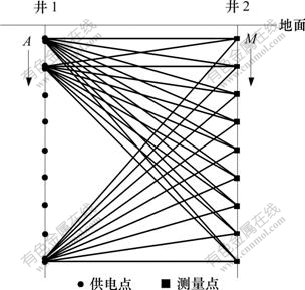
图1  观测系统示意图

Fig.1  Sketch map of observation system

该方法与传统的井间成像方法的不同之处在于成像的原理不同。传统的成像方法借助于雅可比矩阵求出供电点与测量点之间的电位响应关系，从理论上讲，这是一种比较精确的方法，但实际反演效果并不理  想^[17-18]，其原因是反演效果取决于约束条件和迭代 次数。

基于静电场原理，井间电测方法属于“透射”工作方式，当异常体靠近供电源时，异常体吸引或排斥电流强烈，电场分布畸变严重，测量点处能够反映这种变化；根据电场互换原理，当异常体靠近接收点时，异常体的电性特征也会严重影响测量点处的电位。为了在空间上充分展现井间电场的这种分布特征，提出井间几何成像思想：首先，利用镜像法求出与所有电位对应的视电阻率，然后，以观测井深为纵坐标，供电井深为横坐标绘制视电阻率等值线图。在等值线图上，那些圈闭就是异常体的位置，这种图示反映了供电点和测量点之间的映射关系。

另外，由于点电源在非半空间比在地表(半空间)时的电流密度要小，因此，井间二极观测的异常较小。井间电阻率测量与地表测量不同，地表观测是旁侧影响测量，即在异常体上方测量，遇低阻体时，由于吸引电流而使观测点电位降低，但井间测量则相反。井间测量是“对测” 测量，或者说是“透射”测量，遇低阻时由于吸引电流使测量点较其他“等源距”位置上的电位增加，由此计算的视电阻率呈高阻反映。这个结论与模型的实际情况正好相反，数值模拟结果也证实了这一点。因此，在新的成像方法中，高视电阻率异常为低阻体所致，低视电阻率异常为高阻体所致，而且由视电阻率异常形态能够判断异常体的空间形态和精确位置。在测量过程中，当供电电极和测量电极位于同一深度时，距离AM最短，电场最强，如果其间正好存在异常体，则对电流场的扰动最强烈，在此处计算的视电阻率变化最大，这就是该方法纵向分辨率高的原因。

下面利用镜像法求二极装置视电阻率。当在一口井中供电，另一口井中测量，即供电点A和观测点M分别位于2口井中时，地面边界会影响点源A的电流分布，从而影响M点的电位。为了消除地面边界的影响，采用镜像法计算M点处的视电阻率。

二极装置计算示意图如图2所示。假设地面上方与A对称的位置有1个虚电源A′，供电点A与测量点M之间的距离为r，虚电源A′与测量点M之间的距离为r′，x方向与地面平行，z轴垂直于地面向下。由图2可知：

         (1)

         (2)

其中：x_M和z_M分别为M点在x方向和z方向的坐标；x_A和z_A分别为A点在x方向和z方向的坐标。

图2  二极装置计算示意图

Fig.2  Calculation sketch map of two-pole array

由直流点电源公式可得观测点M处的电位为：

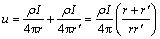          (3)

其中：为视电阻率；I为电源A的电流。整理式(3)，可得：

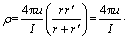
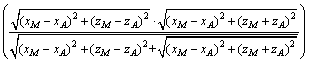 (4)

2  三维数值模拟

在三维空间直角坐标系中，稳定电流场点电源电位满足基本方程^[19-20]：

            (5)

其中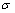：为电导率；u为电位；δ(A)为以A为中心的δ函数。

三维电场的边值问题为：

       (6)

其中：n为电位的外法向；r为电源点至边界的距离。

等价的变分问题是

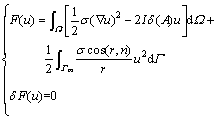     (7)

其中：为无穷远边界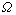；为求解区域。

有限单元法是求解上述三维问题的有效方法。本文选用六面体为网格剖分单元，电位三线性插值，电导率分块均匀。有限单元法计算见文献[19]。

下面计算几种典型模型来说明这种几何成像的效果和应注意的问题。

模型1：2井间距为100 m，井深1 km，井间的中上部有1个低阻体，其长×宽×高为20 m×40 m×80 m，顶部埋深为300 m，离左右井的距离均为40 m。围岩电阻率ρ₀=50 ??m，低阻体电阻率ρ₁=8 ??m，井中电阻率为3 ??m，其剖面图如图3所示。

图3  模型1的剖面图

Fig.3  Profile of model one

图4所示为低阻长方体的计算结果，其中：纵坐标为观测井深，横坐标为供电井深(下同)，浅色区域为标准模型位置。异常形态向右倾斜45?，且呈椭圆状。由于模型位于2井之间的中间部位，当在300 m处供电时，接收点在380 m处得到最大异常；在340 m处供电时，接收点在340 m处得到最大异常，即此时A与M受异常影响最大；在380 m处供电时，接收点在300 m处得到最大异常。因此，异常形态向右倾斜。

模型2：2井间距为100 m，井深1 km，井间的中上部有1个低阻层，其宽×高为30 m×40 m，顶部埋深为220 m。围岩电阻率ρ₀=50 ??m，低阻层电阻率ρ₁=15 ??m，井中电阻率为3 ??m，其剖面图如图5所示。

图4  三维低阻体的视电阻率等值线图

Fig.4  Apparent resistivity isopleth map of 3D low-resistivity body

图5  模型2的剖面图

Fig.5  Profile of model two

图6所示为水平低阻层的视电阻率等值线图，其异常形态近似为“十字星型”。当供电点A与测量点M位于低阻层的上下两侧时，测量点处的异常比较大。特别当供电点A位于220~260 m处，且测量点M也位于220~260 m处时，能够得到最大异常，按照成图方式就形成了“十字星型”异常。

模型3：2井间距为100 m，井深1 km，井间的右下部有1个高阻体，其长×宽×高为20 m×40 m×  80 m，顶部埋深为700 m，距右井的距离为10 m。围岩电阻率ρ₀=50 ??m，高阻体电阻率ρ₁=800 ??m，井中电阻率为3 ??m，其剖面图如图7所示。

图8所示为埋深为700 m的高阻模型的计算结果。如前所述，视电阻率异常中心呈低阻反映，其等值线为水平扁椭圆，原因是高阻体距离测量井太近(10 m)，也就是说大多数供电点都能在测量井的700~780 m处得到明显异常。

图6  水平低阻层的视电阻率等值线图

Fig.6  Apparent resistivity isopleth map of horizontal low-resistivity layer

图7  模型3的剖面图

Fig.7  Profile of model three

图8  三维高阻体的视电阻率等值线图

Fig.8  Apparent resistivity isopleth map of
3D high-resistivity body

模型4：2井间距为100 m，井深1 km，井间的中上部和右下部分别有1个低阻层和1个高阻体。低阻层宽×高为30 m×40 m，其顶部埋深为140 m；高阻体长×宽×高为20 m×40 m×80 m，其顶部埋深为700 m，距右井的距离为10 m。围岩电阻率为50 ??m，低阻层电阻率为10 ??m，高阻体电阻率为1 k??m，井中电阻率为3 ??m。

图9所示为模型4的模拟结果。从图9可以看出：“高阻十字星型”表明是1个水平低阻层，“水平扁椭圆”表明是1个靠近测量井的三维高阻体。组合异常清楚可靠，互不干扰。

图9  组合模型的视电阻率等值线图

Fig.9  Apparent resistivity isopleth map of combination model

模型5：两井间距为100 m，井深1 km，井间深度为320~400 m处有2个模型：左边是1个长×宽×高为20 m×40 m×80 m的高阻体，电阻率为1 k??m，距左井距离为10 m；右边是1个长×宽×高为      20 m×40 m×80 m的低阻体，电阻率为10 ??m，距右井距离为10 m；两异常体相距40 m，围岩电阻率为50 ??m，井中电阻率为3 ??m。

图10所示为同一深度2个异常体的视电阻率等值线图。从图10可以看出：总体异常形态呈“十字”相交；当供电点A位于高阻体附近时，在低阻体附近处上下300 m范围内都有较强异常；同样，当接收点M位于低阻体附近时，在供电点高阻体附近上下300 m范围内也有较强异常。尽管两异常相交，但仍然能够清晰区分。

从对上述模型1~5的计算结果可以看出：本文所采用的井间几何成像效果较好。由于是非半空间，电流密度较小，视电阻率异常差异不是太大。在视电阻率等值线图中，地质模型位置清楚、准确，水平低阻层的异常形态近似为“十字星型”，直立三维高阻体的异常形态近似为“水平扁椭圆”。但是，在所成图像中，高视电阻率反映低阻体，低视电阻率反映高阻体，与地面电法结论相反，必须引起注意。

图10  同一深度2个异常体的视电阻率等值线图

Fig.10  Apparent resistivity isopleth map of two abnormal body at the same depth

3  结论

(1) 提出一种井间几何成像方法，即采用镜像法原理计算非全空间视电阻率，以测量井为纵坐标，供电井为横坐标绘制视电阻率等值线图，成像效果较好，消除了地面影响。

(2) 几何成像方法纵向分辨率较高，横向分辨率较低，能准确确定异常体中心埋深。

(3) 存在的问题是电阻率为视电阻率，目前不能求出真电阻率，这有待进一步研究。

参考文献：

[1] Shima H, Sakayama T. Resistivity tomography: An approach to 2-D resistivity inverse problems[C]//57th Society of Exploration Geophysicists, Expanded Abstracts. Beijing: Petroleum Industry Press, 1989: 204-207.

[2] Daily W, Owen E. Gross-borehole resistivity tomography[J]. Geophysics, 1991, 56(8): 1228-1235.

[3] Shima H. Two-dimensional automatic resistivity inversion technique using alpha centers[J]. Geophysics, 1990, 55(6): 682-694.

[4] Shima H. 2D and 3D resistivity image reconstruction using cross-hole data[J]. Geophysics, 1992, 57(10): 1270-1281.

[5] 周兵, 曹俊兴. 井间电阻率成像数值模拟[J]. 物探化探计算技术, 1995, 17(4): 9-17.

ZHOU Bing, CAO Jun-xing. Numerical modeling for crosshole resisitivity image[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1995, 17(4): 9-17.

[6] 董清华, 田宪谟, 严忠琼. 井间电阻率层析成象的平滑度约束反演[J]. 物探化探计算技术, 1997, 19(2): 122-127.

DONG Qing-hua, TIAN Xian-mo, YAN Zhong-qiong. A smothness-constrained inversion for crosshole resistivity tomography[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1997, 19(2): 122-127.

[7] 董清华, 曹俊兴. 井间电阻率层析成像的几个问题研究[J]. 地球物理学进展, 1998, 13(4): 84-89.

DONG Qing-hua, CAO Jun-xing. Study on some problem for crosshole resistivity tomography[J]. Progress in Geophysics, 1998, 13(4): 84-89.

[8] 董清华. 井间电阻率层析成像的某些进展[J] . 地球物理学进展, 1997, 12(3): 77-89.

DONG Qing-hua. The latest development of cosshole resisitivity tomography[J]. Progress in Geophysics, 1997, 12(3): 77-89.

[9] 吴小平, 徐果明. 利用共轭梯度法的电阻率三维反演研究[J]. 地球物理学报, 2000, 43(3): 420-427.

WU Xiao-ping, XU Guo-ming. Study on 3-D resistivity inversion using conjugate gradient method[J]. Chinese Journal of Geophysics, 2000, 43(3): 420-427.

[10] 黄俊革, 阮百尧, 鲍光淑. 基于有限单元法的三维地电断面电阻率反演[J]. 中南大学学报: 自然科学版, 2004, 35(2): 295-299.
HUANG Jun-ge, RUAN Bai-yao, BAO Guang-shu. Resistivity inversion on 3-D section based on FEM[J]. Journal of Central South University: Science and Technology, 2004, 35(2): 295-299.

[11] 底青云, 王妙月. 积分法三维电阻率成像[J] . 地球物理学报, 2001, 44(6): 844-853.

DI Qing-yun, WANG Miao-yue. 3-D resistivity tomography by integral method[J]. Chinese Journal of Geophysics, 2001, 44(6): 844-853.

[12] 底青云, 王妙月. 电流线追踪电位电阻率层析成像方法初探[J]. 地球物理学进展, 1997, 12(4): 27-34.

DI Qing-yun, WANG Miao-yue. The resistivity tomography by tracing the electric ray[J]. Progress in Geophysics, 1997, 12(4): 27-34.

[13] 白登海, 于晟. 电阻率层析成像理论和方法[J]. 地球物理学进展, 1995, 10(1): 56-75.

BAI Deng-hai, YU Sheng. Theory and methods of resistivity tomography[J]. Progress in Geophysics, 1995, 10(1): 56-75.

[14] 杨华, 李金铭, 桂峰. 电阻率层析成像方法技术近年发展概况[J]. 地球物理学进展, 1998, 13(4): 90-96.

YANG Hua, LI Jin-ming, GUI Feng. The central situation of development for methods and technologies on resistivity tomography in recent years[J]. Progress in Geophysics, 1998, 13(4): 90-96.

[15] 吕玉增, 阮百尧, 黄俊革. 直流电井间三维直接成像[J]. 物探化探计算技术, 2003, 25(1): 60-64.

L? Yu-zeng, RUAN Bai-yao, HUANG Jun-ge. The 3-D immediate crosshole tomography with direct current[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2003, 25(1): 60-64.

[16] 曾文冲, 赵文杰, 臧德福. 井间电磁成像系统研究[J]. 地球物理学报, 2001, 44(3): 411-420.

ZENG Wen-chong, ZHAO Wen-jie, ZANG De-fu. Application research of crosshole electromagnetic tomography[J]. Chinese Journal of Geophysics, 2001, 44(3): 411-420.

[17] 董清华, 田宪谟. 井间电阻率成像中Frèchet导数的算法比较[J]. 物探化探计算技术, 1997, 19(1): 41-45.

DONG Qing-hua, TIAN Xian-mo. A comparision of methods for calculating Frèchet derivatives in crosshole resistivity image[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1999, 19(1): 41-45.

[18] 董清华, 严忠琼. 井间电阻率成像在工程勘察中的应用[J]. 工程勘察, 1998(1): 73-75.

DONG Qing-hua, YAN Zhong-qiong. The application of crosshole resistivity tomography in engineering prospecting[J]. Engineering Prospecting, 1998(1): 73-75.

[19] 强建科, 罗延钟. 三维地形直流电阻率有限元法模拟[J]. 地球物理学报, 2007, 50(5): 1606-1613.
QIANG Jian-ke, LUO Yan-zhong. The resistivity FEM numerical modeling on 3-D undulating topography[J]. Chinese Journal of Geophysics, 2007, 50(5): 1606-1613.

[20] 强建科, 何继善. 椭球体上双频激电法的正演与反演算法[J]. 中南大学学报: 自然科学版, 2007, 38(6): 1199-1205.
QIANG Jian-ke, HE Ji-shan. Algorithm of forward and inversion of dual-frequency induced polarization method on elliptical sphere[J]. Journal of Central South University: Science and Technology, 2007, 38(6): 1199-1205.

收稿日期：2009-05-17；修回日期：2009-07-20

基金项目：国家自然科学基金资助项目(40774057)；国家高科技发展计划(“863”计划)项目(2006AA06Z105，2007AA06Z134)；桂林工学院广西地质工程中心重点实验室开放基金资助项目(07109011-K019)

通信作者：强建科(1967-)，男，陕西岐山人，副教授，从事地球物理电磁法研究；电话：13548985729；E-mail: qiangjianke@163.com

(编辑 赵俊)