DOI: 10.11817/j.ysxb.1004.0609.2020-37612

基于细观损伤力学的铅套成形破裂预测

徐戊矫，谢  丹，李  芳，高元鹏

(重庆大学 材料科学与工程学院，重庆 400044)

摘  要：对子弹铅套成形过程中的破裂缺陷进行预测。采用单向拉伸实验获得纯铅真实应力-应变数据，选取应变0.006≤ε≤0.2范围内的数据进行拟合和外延处理获得材料无损伤的本构模型。结合扫描电镜分析法和基于响应面的有限元反求法获得纯铅的GTN细观损伤模型参数，对比分析单向拉伸中模拟与实验获得的载荷-位移曲线和铅材料孔洞体积分数，验证了所建立的纯铅GTN细观损伤模型的准确性。基于ABAQUS模拟仿真平台，耦合所建立的GTN损伤模型对铅套成形过程中的破裂行为进行仿真预测，并开展了铅套反挤压和变薄拉深成形实验。结果表明：实验结果与基于GTN损伤模型的仿真结果匹配良好；对铅套成形缺陷的准确预测是铅套成形优化的重要基础。

关键词：铅套成形；GTN细观损伤模型；响应面法；扫描电镜；破裂预测

文章编号：1004-0609(2020)-08-1866-10　　     中图分类号：TB31　　     文献标志码：A

金属塑性变形过程中，材料内部细观层面的损伤主要是微孔洞。TVERGAARD等^[1]和NEEDLEMAN等^[2]在GURSON^[3]研究的基础上，考虑了孔洞的聚合和孔洞之间的相互作用，引入孔洞体积分数的概念对Gurson模型进行了进一步地修正，提出了目前应用最为广泛的GTN模型。

GTN损伤模型参数众多，不同材料的GTN模型参数也不同。只有获得正确的GTN参数，才能获得这种材料孔洞演化的过程和损伤力学性能。ABBASSI等^[4]通过有限元模拟和人工神经网络的方法标定了304不锈钢的GTN损伤参数，通过响应面法和基于遗传算法的有限元反向标定了IF钢的GTN损伤参数。SIRINAKORN等^[5]采用代表性体积单元法，确定了DP双相钢的GTN损伤参数。黄建科等^[6]通过建立关于载荷位移曲线的误差函数，来获得GTN模型的参数，并基于体胞模型推导出断裂临界应变的表达式。陈志英^[7]针对各向异性板料冲压的问题，建立了Barlat89-GTN和Hill48-GTN各向异性材料的细观损伤模型，并反向确定GTN参数，用于表征各向异性板料在拉深过程中回弹和破裂的问题。BROGGIATO等^[8]提出了一种较为新颖的损伤参数获取方法，通过数字图形法来确定GTN损伤模型的参数。学者ABBASI等^[9]利用四因子三水平的响应面，选取拉深试验后的载荷位移曲线上四个关键的点作为响应的目标值，并利用Minitab软件确定了GTN模型中的损伤参数。何敏等^[10]采用Image-Pro Plus图像分析软件来分析扫描电镜的图片，确定了5052铝合金的f₀、f_C和f_F损伤参数，并得出有限元分析法与GTN损伤模型结合可有效预测成形极限曲线。刘文权和盈亮等^[11-12]采用响应面中心复合试验和遗传算法，确定了热成型高强钢22MnB5在高温下(600~800 ℃)的GTN损伤参数。

子弹弹头中的铅套，其作用是为了防止子弹在射击过程中弹头钢芯高速旋转，直接与弹头壳摩擦，造成弹头在射击过程中破坏失效；同时，铅套能有效提高子弹的杀伤力。但是纯铅的质地软、强度低，因此在铅套成形过程中容易出现破裂等问题。本文以某型号弹头中的铅套为研究对象，基于ABAQUS模拟仿真平台，耦合所建立的GTN损伤模型对铅套成形过程中的破裂行为进行仿真预测。开展了铅套反挤压和变薄拉深成形实验，将实验结果与基于GTN损伤模型的仿真结果进行了对比分析。

1  GTN细观损伤模型

GTN细观损伤模型是用孔洞体积分数来表征材料的损伤，并引入到材料屈服函数中，因此可以更好地预测材料在整个变形过程中的损伤行为。

GURSON^[3]首次提出的Gurson损伤模型是GTN损伤模型的前身，他第一次建立了孔洞演变规律和材料塑性势函数之间的关系，并将孔洞体积分数的概念引入到材料的屈服准则中，提出了包含材料孔洞体积分数的屈服函数：

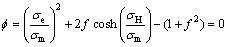         (1)

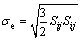                                 (2)

式中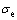：表示材料宏观Von Mises等效应力；S_ij表示应力偏张量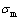；表示当前基体的等效屈服应力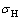；表示宏观静水应力；f表示基体材料的孔洞体积分数。当f等于0时屈服函数式(1)就变为最经典的Von Mises屈服函数。

Gurson模型是将材料的屈服与损伤联系起来，随着基体材料孔洞体积分数的不断增加，屈服面将逐渐减少，从而材料的强度随着损伤的增加而不断退化，直至材料发生断裂失效。

TVERGAARD等^[1]和NEEDLEMEN等^[2]对Gurson损伤模型进行了修正，引入等效孔洞体积分数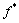和屈服函数的修正系数q₁、q₂、q₃，为目前应用最为广泛的GTN细观损伤模型，如式(3)所示：

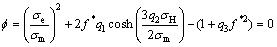  (3)

式中：q₁、q₂、q₃表示屈服函数修正系数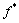；表示等效孔洞体积分数，它是一个关于孔洞体积分数f的函数，其表达式为

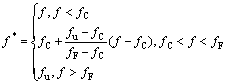         (4)

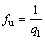                                       (5)

式中：f_C表示孔洞聚合时的临界体积分数；f_F表示材料断裂失效时的孔洞体积分数。当材料中孔洞体积分数超过孔洞聚合时的临界体积分数f_C时，孔洞开始聚合，材料孔洞体积分数迅速增加，材料的承载能力开始迅速降低。当材料的孔洞体积分数达到断裂孔洞体积分数f_F时，材料发生宏观的裂纹，将彻底失去承载能力。

孔洞的演化分为三个阶段：孔洞的形核、长大和聚合阶段。因此孔洞体积分数f的增加分为两个部分，分别是新孔洞的形核和孔洞的长大，所以孔洞的增量表达式为：

                       (6)

孔洞生长的表达式为：

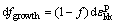                           (7)

基于塑性应变的形核机制，孔洞形核表达式为：

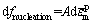                             (8)

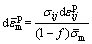                              (9)

式中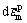：表示材料等效塑性应变的增量；A是表示材料孔洞形核强度的正态分布函数，其函数表达式为

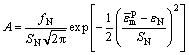              (10)

式中：f_N表示材料孔洞形核粒子的体积分数；S_N表示孔洞形核发生时等效塑性应变的标准差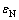；表示材料孔洞形核发生时平均等效塑性应变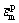；表示材料在变形过程中累积的等效塑性应变。

GTN细观损伤模型中损伤变量即孔洞体积分数有明确的物理意义和几何意义，该模型将基体材料的损伤与材料的塑性变形紧密联系在一起。

2  铅力学性能测试

本研究利用挤压获得圆柱形纯铅棒料，并通过轧制获得铅板。采用电火花线切割机，线切割轧制后的铅板截取准静态拉伸试样，拉伸试样尺寸参考GB/T 228—2002《金属拉伸实验方法》中规定的拉伸试样尺寸，如图1所示。室温准静态拉伸实验在CMT5305型电子万能拉伸实验机上进行，拉伸速度采用恒定的6 mm/min，并一直加载至拉伸试样断裂为止。拉伸实验数据均取3组稳定实验的平均值。原始拉伸试样和拉伸后的试样如图2所示。

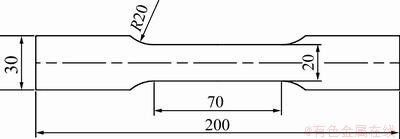
图1  拉伸试样尺寸

Fig. 1  Tension specimen size (Unit: mm)

图2  原始拉伸试样和拉伸后的试样

Fig. 2  Original and post-tension specimens

用单向拉伸全过程试验数据计算得到的真实应力-应变数据是包含了材料损伤演化影响的，用其建立GTN模型并耦合进行成形过程数值模拟时，会造成模拟结果误差较大。因此，为保证仿真结果更加贴合实际情况，需要使用基体材料无损伤的应力-应变数据作为材料的本构模型^[13]。在单向拉伸的初期阶段材料损伤较小，实验测得单向拉伸初期的材料真实应力-应变曲线更为贴近材料的无损伤状态。可以利用材料的本构方程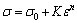，通过数据拟合将单向拉伸初期的材料真实应力-应变曲线作为基体材料无损伤的真实应力-等效塑性应变关系。

图3  不同应变下单向拉伸试样截面的孔洞体积分数

Fig. 3  Void volume fraction of uniaxial tension specimens with different strains

拟合材料无损伤的本构模型时，如何选择恰当的应变点区间很关键。首先需保证选择的区间处于塑性应变下，因此选择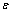≥0.006。对发生不同应变量的单向拉伸试样进行扫描电镜观察，并对不同应变量下试样的孔洞体积分数进行统计分析，如图3所示。从图3可以看出，应变0.2是一个临界点；当应变为0.2时基材内微观孔洞较少、分布均匀，且并未发生聚合。为保证拟合得到的材料应力-应变曲线更贴近材料无损伤状态下，因此本研究中选取的应变拟合点间距为[0.006，0.2]，拟合结果如图4所示，表1中所列为纯铅的弹塑性力学行为参数，其中E表示为材料的弹性模量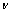；表示为材料的泊松比；σ₀表示材料的屈服应力；K表示该材料本构参数；n表示材料的硬化指数。

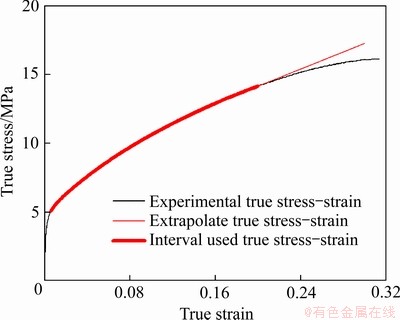
图4  纯铅无损伤应力-应变曲线的获取

Fig. 4  Acquisition of damage free stress-strain curves of pure lead

表1  纯铅的无损伤弹塑性力学参数

Table 1  Damage-free elastoplastic behavior parameters of pure lead

3  GTN参数的标定

GTN细观损伤模型中包含三类共计9个参数，分别是屈服函数的修正系数q₁、q₂、q₃，孔洞形核参数f_N、ε_N、S_N和孔洞体积分数f₀、f_C、f_F。其中，f_N表示形核粒子的孔洞体积分数，S_N为形核时的等效塑性应变，S_N是形核应变的标准差，f₀表示材料初始的孔洞体积分数，f_C表示孔洞聚合时的临界体积参数，f_F表示材料发生破坏失效时的孔洞体积分数。不同的参数组合对模拟结果的影响较大，因此，确定一种材料的GTN损伤模型参数是研究这种材料孔洞演化过程和细观损伤机理的基础。目前确定GTN细观损伤模型参数的方法大致分为三类^[14-16]：金相分析法、代表性体积单元法和有限元逆向法。

在这里，假设挤压得到的圆柱形纯铅的棒料是无损伤材料，因此铅的初始孔洞体积分数f₀取值0。q₂和q₃根据TVERGAARD的研究结果，取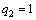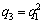，。形核应变的标准差S_N对于一般的韧性材料可以取值为0.1，即S_N=0.1。本文通过SEM扫描电镜分析法和基于响应面有限元反求法相结合的方式来获取铅其余5个GTN损伤模型参数(q₁、f_N、ε_N、f_C 、f_F)。

3.1  扫描电镜分析法

图3所示为铅拉伸试样断口的扫描电镜图片。从图3中可以观察到，铅断口处有明显的韧窝分布。

通过Image-Pro Plus软件对铅断口的扫描电镜图片进行分析，可以计算铅断口扫描电镜图片上孔洞的面积百分比。但散布在真实材料中的孔洞是三维的，为获得断口处的孔洞体积分数，假设基体材料中任一孔洞的形状是规则的球形，通过截取基体材料的任一平面，获得单位面积内的孔洞个数为N_s，在该截面的单位高度内的孔洞个数为N_h.。假设该截面内的任意一个孔洞的半径为r，那么该截面内任意一个孔洞的截面面积的范围在0~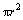之间。根据概率论的知识，可以求得所截截面的孔洞平均面积为：

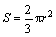                              (11)

该截面孔洞半径为：

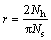                                (12)

单位面积内的孔洞面积分数为：

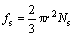                               (13)

单位体积内的孔洞体积分数为：

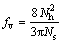                                (14)

孔洞面积分数和体积分数的关系为：

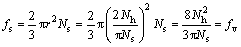      (15)

通过公式(15)，可以推导统计得到的扫描电镜图片中孔洞面积分数和孔洞体积分数是相等的，因此可以通过测量计算SEM像中孔洞的面积百分比来确定材料该处的孔洞体积分数。通过测量并取平均值可以得到断口处孔洞体积分数为10%，因此认为本文中铅断裂时的孔洞体积分数f_F为0.1，即f_F=0.1。

3.2  有限元反求法

在利用扫描电镜分析法获得了铅断裂时的孔洞体积分数f_F以后，借助响应面法，利用ABAQUS模拟仿真软件进行单向拉伸的有限元模拟仿真，反求损伤参数q₁、f_N、ε_N、f_C。响应面法是通过建立响应值与损伤参数之间的二次多项式模型进行回归分析，其一般表达式为：

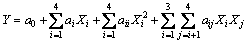     (16)

式中：Y是响应面的响应值；a₀为常数，a_i、a_ii和a_ij分别为回归模型的一次项、二次项和交叉项的系数；X_i、X_j代表损伤参数q₁、f_N、ε_N、f_C。本文中响应目标值选取拉伸试验得到的载荷-位移曲线上的5个点，如图5所示，分别为最大拉伸载荷处的拉伸位移(R₁)、最大拉伸载荷(R₂)、承载能力迅速下降时的拉伸位移(R₃)、承载能力迅速下降时的拉伸载荷(R₄)和断裂失效时的拉伸位移(R₅)。

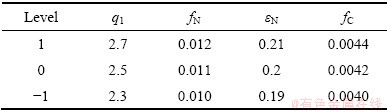
通过多次模拟结果的比对，确定出损伤参数的高水平(1)、中间水平(0)和低水平(-1)，如表2所示。

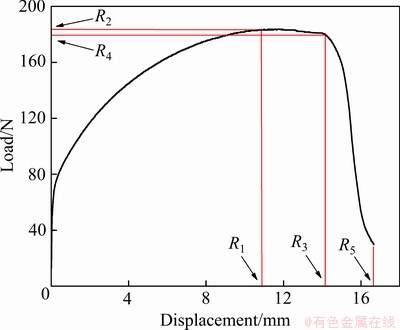
图5  载荷-位移曲线中响应值的选取

Fig. 5  Selection of response value

表2  损伤参数高低水平的选取

Table 2  Selection of high and low levels of damage parameters

本文通过Minitab软件设计了27组试验，并基于ABAQUS平台对这27组试验进行仿真模拟，从模拟结果中获取对应的5个响应目标值，最终结果如表3所示。模拟中纯铅的密度为ρ=11.4 g/cm³。模拟仿真的拉伸试样与图1的尺寸完全相同，并且设置的边界条件与实际拉伸试验一致。有限元模型中单元类型采用带有沙漏控制的8节点缩减积分体单元(C3D8R)。最终获得5个响应值的回归模型，如式(17)所示：

  (17)

对回归模型进行方差分析，其结果如表4所示。其中5个响应目标值的P值均小于0.01，R²(R-sq)均大于90%，证明该模型显著，拟合程度较好并具有统计学意义，能较好地反应各个损伤参数与响应面目标值的关系。将真实试验获得的响应值作为目标值带入回归模型方程中，从而求得最佳的损伤参数q₁=2.64、ε_N=0.21、f_N=0.0109、f_C=0.00432。

通过扫描电镜分析法和基于响应面的有限元反求法最终得到了纯铅GTN损伤模型参数如表5所示。

3.3  验证GTN参数的准确性

为验证3.2小节中获得的纯铅GTN损伤模型参数的准确性，将GTN模型耦合到单向拉伸模拟中。将单向拉伸模拟与实验获得的载荷-位移曲线和铅材料孔洞体积分数进行对比，以验证所建立的纯铅GTN模型中参数的准确性。

从图6可以看出，试验获得的载荷-位移曲线和模拟结果匹配良好。通过单向拉伸试验获得不同应变量下的拉伸试样，应变量分别为0.1、0.2、0.3、0.35。针对上述拉伸试样，对将发生缩颈或已发生缩颈处的截面进行扫描电镜观察，获得对应的SEM像，如图3所示。通过Image-Pro Plus软件，统计截面的孔洞体积分数，将其与模拟仿真获得的孔洞体积分数随等效塑性应变的数据进行对比，如图7所示。从图7可以看出，实验获得的铅材料孔洞体积分数随应变的变化规律与模拟结果吻合较好。

表3  有限元模拟试验设计方案

Table 3  Test design scheme of finite element simulation

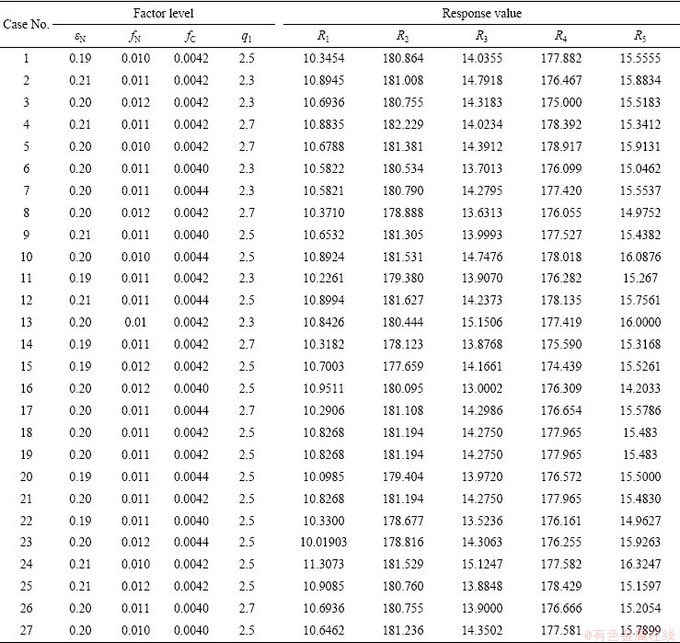
表4  回归模型方差分析结果

Table 4  Analysis of variance of model

通过分别对比模拟与实验获得的载荷-位移曲线和铅材料孔洞体积分数随应变的变化规律，验证了获得的铅GTN模型准确性较好；将其耦合到铅套成形模拟过程中，以预测铅套成形过程的破裂行为。

表5  铅的GTN细观损伤模型参数

Table 5  GTN damage parameters of lead

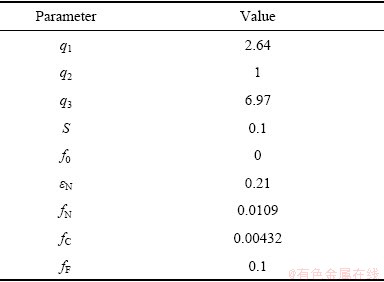
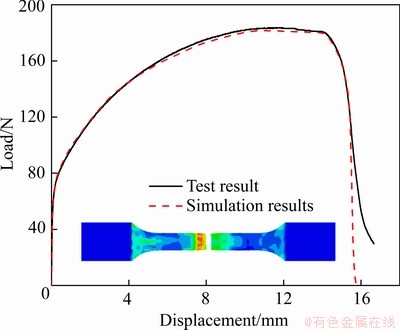
图6  单向拉伸模拟与实验的载荷-位移曲线对比

Fig. 6  Comparison of load-displacement curves between simulation result and test result

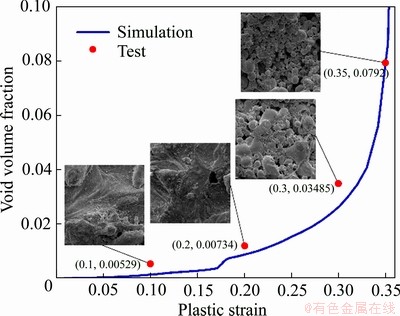
图7  铅材料孔洞体积分数的模拟与实验结果对比

Fig. 7  Comparisons between simulation and experimental results of void volume fraction for Lead

4  铅套破裂行为的预测

铅套成形的工艺方案为：反挤压→变薄拉深，两个步骤均是在室温下成形。为预测铅套成形过程中的损伤行为，在ABAQUS平台上，将求得的纯铅GTN模型耦合进铅套成形的模拟仿真中。为了提高计算速度，采用2D模型，模具设置成Analytical rigid模型，并约束住凹模的6个方向上的自由度。坯料设置为Deformable分析模型。利用ABAQUS动态显示求解器进行仿真模拟，网格采用C3D8R，并加入ALE网格自适应技术。模拟过程的摩擦因数取值为0.15，冲头的下压速度为8 mm/s。

用孔洞体积分数来表征材料的损伤。如图8所示，在反挤压后期，最大的孔洞体积分数集中在口部，但未到材料失效时的孔洞体积分数0.1。但在变薄拉深的成形模拟中，如图9所示，当冲头下压行程达到14 mm时，铅套筒壁处的孔洞体积分数达到失效时的数值0.1。基于模拟分析结果，推断铅套在变薄拉深时发生了破裂损伤。图10(c)中的模拟结果显示，铅套的破裂失效主要集中在筒壁处，预测会发生明显的拉裂现象。

根据铅套成形的工艺方案开展了铅套成形实验。图10所示分别为反挤压和变薄拉深后的铅套成形结果。由图10可以发现，反挤压过后除了口部不规整之外铅套筒壁完好，但变薄拉深后铅套出现拉裂现象。与耦合GTN模型的模拟结果对比发现，模拟结果与试验结果匹配良好。耦合GTN损伤模型的数值模拟可以对铅套成形过程中的破裂损伤行为进行较准确地预测。

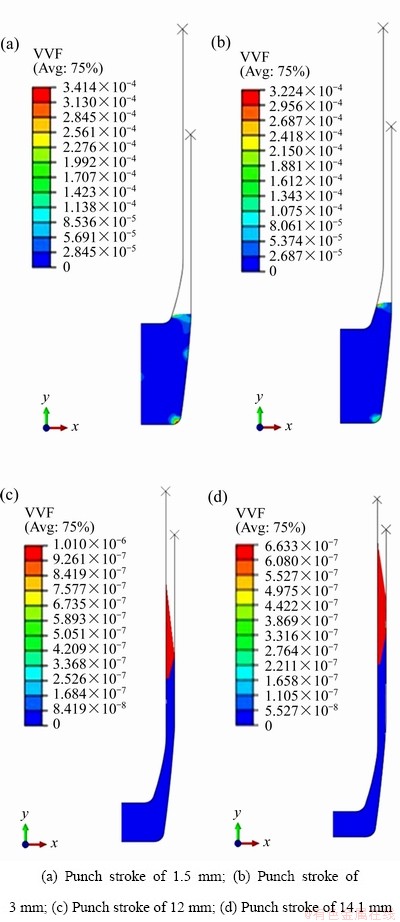
图8  反挤压过程中铅套的孔洞体积分数模拟结果

Fig. 8  Simulation results of void volume fraction in backward extrusion

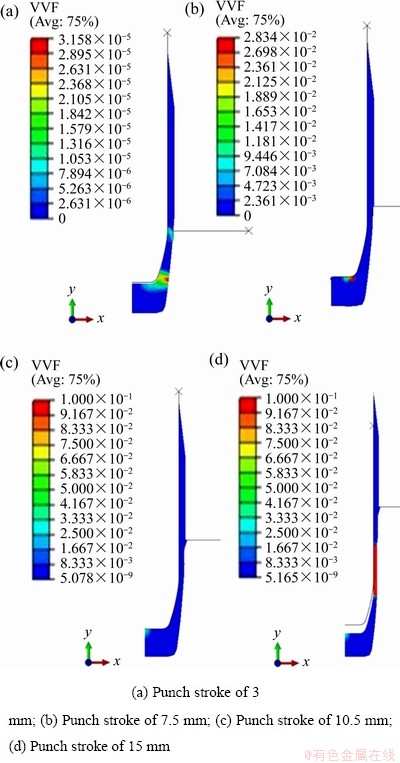
图9  变薄拉深过程中铅套的孔洞体积分数模拟结果

Fig. 9  Simulation results of void volume fraction in lead sleeve during thinning and deep drawing

图10  铅套成型模拟和实验结果比对

Fig.10  Comparison between simulation and test results for formation of lead sleeve

5  结论

1) 通过单向拉伸试验数据获得纯铅真实应力-应变数据，选取应变0.006≤ε≤0.2范围内的数据进行拟合和外延处理获得材料无损伤的本构模型，作为耦合GTN模型进行铅套成型数值模拟仿真的材料属性。

2) 将扫描电镜分析法和基于响应面的有限元反求法相结合，获得了纯铅材料的GTN细观损伤模型参数：f_F=0.1，q₁=2.64，ε_N=0.21，f_N=0.0109，f_C=0.00432。通过分别对比模拟与实验获得的载荷-位移曲线和铅材料孔洞体积分数，验证了获得的铅GTN模型参数的准确性较好。

3) 在ABAQUS平台上，耦合获得的纯铅材料GTN细观损伤模型，模拟了铅套的成形过程，用材料的孔洞体积分数来表征铅套在成形过程中材料的损伤行为。通过模拟预测出，变薄拉深后铅套在壁部会出现拉裂现象。实际的铅套成型实验结果与模拟结果匹配良好。耦合GTN损伤模型的数值模拟可以对铅套成形过程中的破裂损伤行为进行较准确的预测。这是其后续成形优化工作的重要基础。

REFERENCES

[1] TVERGAARD V, NEEDLEMAN A. An analysis of the cup-cone fracture in a round tensile test bar[J]. Acta Metall, 1984, 32(1): 157-169.

[2] NEEDLEMAN A, TVERGAARD V. An analysis of ductile rupture in notched bars[J]. Journal of the Mechanics and Physics of Solids, 1984, 32(6): 461-490.

[3] GURSON A L. Continuum theory of ductile rupture by void nucleation and growth: Part Ⅰ Yield criteria and flow rules for porous ductile media[J]. Engng Mater Technol, 1977, 99(1): 2-15.

[4] ABBASSI F, BELHADJ T, MISTOU S, ZGHAL A. Parameter identification of a mechanical ductile damage using Artificial Neural Networks in sheet metal forming[J]. Materials & Design, 2013, 45: 605-615

[5] SRIRNAKORN T, WONGWISES S, UTHAISANGSUK V. A study of local deformation and damage of dual phase steel[J]. Materials and Design, 2014, 64: 729-742.

[6] 黄建科, 董湘怀. 金属成形过程的细观损伤力学模型及韧性断裂准则研究[D]. 上海: 上海交通大学, 2009.

HUANG Jian-ke, DONG Xiang-huai. Research on meso damage mechanics model and ductile fracture criterion of metal forming process[D]. Shanghai: Shanghai Jiao Tong University, 2009.

[7] 陈志英. 冲压成形中破裂和回弹的细观损伤力学分析[D]. 上海: 上海交通大学, 2009.

CHEN Zhi-ying. Meso damage mechanics analysis of fracture and spring back in stamping forming[D]. Shanghai: Shanghai Jiao Tong University, 2009.

[8] BROGGIATO G B, CAMPANA F, CORTESE L. Identification of material damage model parameters: An inverse approach using digital image processing[J]. Meccanica, 2007, 42(1): 9-17.

[9] ABBASI M, BAGHERI B. Application of response surface methodology to drive GTN model parameters and determine the FLD of tailor welded blank[J]. Computational Materials Science, 2012, 53(1): 368-376.

[10] HE Min, LI Fu-guo, WANG Zhi-gang. Forming limit stress diagram prediction of aluminum alloy 5052 based on GTN model parameters determined by in situ tensile test[J]. Chinese Journal of Aeronautics, 2011, 24(3): 378-386.

[11] 刘文权, 盈 亮, 王丹彤, 鲁可心, 胡 平. 热冲压成形过程细观损伤演化机理研究[J]. 机械工程学报, 2016, 52(14): 31-39.

LIU Wen-quan, YING Liang, WANG Dan-tong, LU Ke-xin, HU Ping. Study on meso damage evolution mechanism of hot stamping process[J]. Journal of Mechanical Engineering, 2016, 52 (14): 31-39.

[12] 盈 亮, 刘文权, 王丹彤, 胡 平, 王 琪. 7075-T6铝合金温成形损伤演化实验与仿真[J]. 中国有色金属学报, 2016, 26(7): 1383-1390.

YING Liang, LIU Wen-quan, WANG Dan-tong, HU Ping, WANG Qi. Damage evolution experiment and Simulation of 7075-T6 aluminum alloy during warm forming [J]. Chinese Journal of Nonferrous Metals, 2016, 26(7): 1383-1390.

[13] CUESTA I I, ALEGRE J, LACALLE R. Determination of the Gurson-Tvergaard damage model parameters for simulating small punch tests[J]. Fatigue & Fracture of Engineering Materials & Structures, 2010, 33(11): 703-713.

[14] STEGLICH D, BROCKS W. Micromechanical modelling of the behaviour of ductile materials including particles[J]. Computational Materials Science, 1997, 9(1/2): 7-17.

[15] MAHNKEN R. Aspects on the finite-element implementation of the Gurson model including parameter identification[J]. Avian Diseases, 1997, 41(2): 326-329.

[16] 闫玉曦. 带钢边部缺陷在轧制过程中的开裂行为研究[D]. 上海: 华东理工大学, 2014.

YAN Yu-xi. Study on cracking behavior of strip edge defects during rolling[D]. Shanghai: East China University of Science and Technology, 2014.

Fracture prediction of lead sleeve based on mesoscopic damage mechanics

XU Wu-jiao, XIE Dan, LI Fang, GAO Yuan-peng

(Chongqing University, College of Materials Science and Engineering, Chongqing 400044, China)

Abstract: The fracture prediction in the forming process of bullet lead sleeve was studied. The true stress-strain data of pure lead were obtained by uniaxial tensile test, in which the strain range of 0.006≤ε≤0.2 was selected for fitting and extrapolating to obtain the damage free constitutive relationship. The parameters of the GTN micro-damage model of pure lead were acquired by means of scanning electron microscopy analysis and inverse finite element simulation based on response surface method. The load displacement curve and void volume fraction of lead material obtained by simulation and experiment in uniaxial tension were compared and analyzed, which verified the accuracy of the parameters in the GTN model of pure lead. Based on ABAQUS simulation platform, coupled with the GTN damage model, the fracture behavior of lead sleeve during forming process was simulated and predicted. The experiments of back extrusion and thinning deep drawing for lead sleeve were carried out. The results show that the experimental results match well with the simulation results based on GTN damage model. The accurate prediction of forming defects of lead sleeve is an important basis for forming optimization.

Key words: formation of lead sleeve; GTN micro-damage model; response surface method; scanning electron microscope; fracture prediction

Received date: 2019-07-26; Accepted date: 2020-07-24

Corresponding author: XU Wu-jiao; Tel: +86-13368186252; E-mail: xuwujiao_cq@163.com

(编辑  何学锋)

收稿日期：2019-07-26；修订日期：2020-07-24

通信作者：徐戊矫，教授，博士；电话：13368186252；E-mail：xuwujiao_cq@163.com