一种用于UWB接收端的带通滤波器分析与设计
王斌1,吴伟仁1,曲毓萱2,陈志发3
(1. 中国科学院电子学研究所,北京,100190;
2. 中国兵器工业新技术推广研究所,北京,100089;
3. 香港应用科技研究院有限公司,香港,999077)
摘要:采用0.18 μm工艺设计1个用于UWB接收端的4阶切比雪夫有源RC带通滤波器。给出1种有损积分器直流增益补偿策略,从而减小滤波器对运算放大器直流增益的要求。同时,采用1种数控电阻的方式实现通带增益的调节。仿真结果表明:所设计的滤波器在通带增益为0 dB时,通带纹波增益为0.112 dB,下-3 dB频率为156 kHz,上-3 dB频率为259 MHz,带宽为258.844 MHz;频率为500 MHz处的信号衰减为28.25 dB,频率为792 MHz处的信号衰减为45.16 dB,完全符合UWB接收端对带通滤波器的性能指标要求。
关键词:超宽带;带通滤波器;通带纹波
中图分类号:TN432 文献标志码:A 文章编号:1672-7207(2012)02-0554-07
Analysis and design of a band-pass filter for UWB receiver
WANG Bin1, WU Wei-ren1, QU Yu-xuan2, CHEN Zhi-fa3
(1. Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China;
2. Advanced Technology Generalization Institute of CNGC, Beijing 100089, China;
3. Hong Kong Applied Science and Technology Research Institute Co. Ltd., Hong Kong 999077, China)
Abstract: A forth-order Chebyshev active RC band-pass filter was designed in 0.18 μm process for ultra-wide band (UWB) receiver. A DC-Gain compensation scheme for lossy integrator was presented to relax the requirement for the DC gain of the op-amp. Meanwhile, a pass-band gain tuning structure was implemented by adopting digital controlled resistor tank. The results show that when the pass-band gain of the filter is tuned to 0 dB, ripples of filter is 0.112 dB, lower -3 dB frequency is 156 kHz, upper -3 dB frequency is 259 MHz, bandwidth is 258.844 MHz, attenuation is 28.25 dB at 500 MHz and is 45.16 dB at 792 MHz. All these results meet the specifications of the band-pass filter for UWB receiver completely.
Key words: ultra-wide band (UWB); band-pass filter; pass-band ripple
超宽带(Ultra-wide band,UWB)无线通信技术是一种高数据率、低功耗的短距离无线通信技术,近年来成为国内外研究的热点之一[1-3]。美国联邦通信委员会(Federal Communications Commission,FCC)根据IEEE802.15a物理层标准规定3.1~10.6 GHz 为免费频段。作为UWB设备的主要工作频段,该频段被划分为14个子段,每个子段占用频宽528 MHz[4]。在超宽带系统中,滤波器是信号处理系统中的重要模块,根据美国联邦通信委员会的规定[5]:频谱成型时,滤波器在通带内的插入损耗应当尽量小;在带外,滤波器要同时实现干扰抑制和频谱成型2种功能。UWB要求滤波器在110%的相对带宽内具有良好的幅频、相频特性。而传统设计方法中,不论是低通到带通的频率变换,还是分布参数元件近似为集总元件,都是非线性变换,在中心频点附近误差较小,偏离中心频点后误差迅速增大;其次,当带宽增加时,微带平行耦合线等结构构造的谐振单元将变得难以实现,以至当相对带宽达到20%~30%时,工艺上已经很难实现。因此,传统滤波器的设计方法和实现方法已难以适应UWB带宽的需求[6]。随着大规模集成电路及互补金属氧化物半导体(Complementary metal oxide semiconductor,CMOS)工艺的发展,芯片的功能越来越多样化,低功耗高性能的CMOS片上滤波器与系统芯片集成成为必然。片上滤波器的实现方式有无源滤波器和有源滤波器2种,无源滤波器噪声低,线性度高,工作频率高,但是,片上实现电感会占用很大芯片面积,而且电感的品质因素Q低,频率不易调谐。采用跨导-电容(Gm-C)有源滤波器结构易于实现高频率的滤波器,但其线性度受运算放大器的影响较大,需要高线性度的运算放大器,增大了滤波器的设计难度和功耗[7]。与上述类型的滤波器相比,有源电阻-电容(R-C)滤波器具有以下2个优点:(1) 运算放大器的输入是虚地,因此,对于输入范围要求并不那么严格,这有利于提高设计的线性度; (2) 对每个运算放大器的要求是一致的,因此,设计过程中只需要设计1个运放,大大减小了设计的复杂度[8-9]。在此,本文作者采用有源R-C方式和状态变量法设计了1个用于UWB接收端的带通滤波器。所采用的结构只包含有损积分器,通过采用本文给出的积分器直流增益补偿策略,部分地补偿了由于运算放大器有限直流增益引起的误差,降低了滤波器对运算放大器直流增益的要求。此外,通过采用数字控制的方式,方便地实现了对滤波器通带增益的调节。
1 积分器直流增益补偿策略
积分器是滤波器的基本模块,包括无损积分器和有损积分器2类。由于无损积分器的直流增益依赖于运算放大器的直流增益,因而,受工艺、温度、电源电压影响比较大,很难做得精准,这将直接影响滤波器的通带响应;另一方面,无损积分器的通带较窄,有用信号也随着噪声一起被衰减。一个理想的有损积分器如图1所示,其传输函数为:
 (1)
(1)
由式(1)可知:理想积分器的直流增益由电阻之比决定,所以,精度很高且对工艺和环境的影响不敏感。而通带宽度(主极点)由电阻R2和电容C的乘积决定并可以调节,带内增益基本上为常数。图2所示为仅考虑运放有限直流增益的实际有损积分器,其传输函数为:
 (2)
(2)
从式(2)可以看出:该有损积分器的直流增益与运放的直流增益A有关,且A越大,该积分器越接近理想有损积分器;同时,A也影响通带宽度。
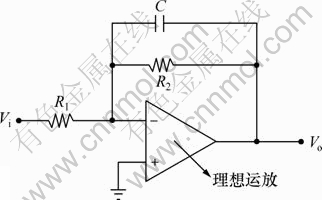
图1 理想有损积分器
Fig.1 Ideal lossy integrator

图2 仅考虑运放有限直流增益的有损积分器
Fig.2 Lossy integrator using op-amp which only includes finite DC gain
为了减小运放直流增益对有损积分器的影响,本文给出了一种有损积分器直流增益补偿策略。在式(2)中,若令
 (3)
(3)
则
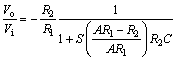 (4)
(4)
对比式(4)和式(1)可知:通过合理选择积分电阻R3,有损积分器的直流增益对运放直流增益的依赖可以在一定程度上减小(因为R3最优值仍然受运放直流增益的影响)。而采用上述补偿策略后,通带宽度相对于理想有损积分器略微上升,但只要运放直流增益保持在合理的范围内,这种影响可忽略不计。图3给出了当有损积分器的直流增益绝对值设定为1(即0 dB)时,采用理想运算放大器(图3(a))和直流增益为40 dB的实际运算放大器(图3(b))构成的有损积分器的频率响应。从图3可以看出:在有损积分器的直流增益接近0 dB时,两者对应的频率分别为1.00 Hz和3.35 Hz;它们的主极点分别位于1.59 GHz和1.60 GHz。这说明通过采用上述补偿策略,有效地降低了有损积分器对运算放大器直流增益的要求。
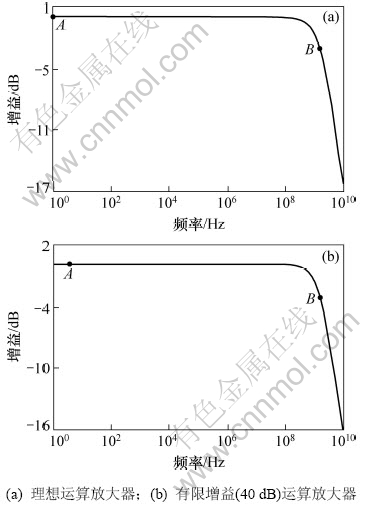
图3 采用理想运算放大器和有限增益(40 dB)运算放大器构成的有损积分器的频率响应(积分器直流增益设定为0 dB)
Fig.3 Frequency response of lossy integrator with ideal op-amp and with finite gain (40 dB) op-amp (the DC gain of the lossy integrators is 0 dB)
2 带通滤波器的系统级设计
表1所示为UWB接收端对带通滤波器的性能指标。尽管切比雪夫滤波器的通带衰减比最大平坦型的要大,但其带外衰减特性的上升陡度很大,具有较好的过渡带特性[10-12]。因此,本文采用4阶切比雪夫滤波器结构,其信号流图如图4所示。其中:a/(s+b)表示有损积分器的传输函数;a和b分别表示该积分器传输函数分子与分母的常数项;f0~f3表示从各积分器输出端反馈到加法器的反馈增益;f4表示输入信号到加法器的前向增益。采用梅森公式可计算出该滤波器的信号传输函数为:
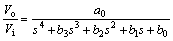 (5)
(5)
表1 UWB接收端带通滤波器性能指标要求
Table 1 Specifications of UWB Receiver Band-Pass filter


图4 4阶切比雪夫带通滤波器信号流图
Fig.4 Signal flow diagram of forth-order Chebyshev band-pass filter
各系数a0,b0~b3又可以用信号流图内的各参数a,b和f1~f4表示为:
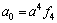 (6)
(6)
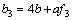 (7)
(7)
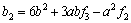 (8)
(8)
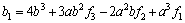 (9)
(9)
 (10)
(10)
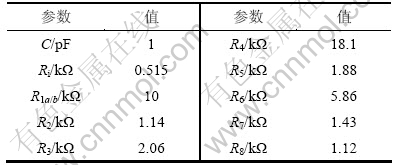
通过MATLAB计算可得上述各参数值如表2所示。
表2 滤波器信号流图与传输函数的各参数值
Table 2 Parameters of filter signal flow and transfer function diagram

从图4可以推断出:所设计的滤波器包含4个有损积分器和1个加法器,因而需要5个运放。然而,第5,3和2积分器输出端反馈到加法器的反馈增益f0,f1和f2以及输入信号到加法器的前向增益f4均太大,且由于该增益由电阻的比值决定,如此大的电阻比值难以保证,因此,加法器由2个运算放大器级联构成以降低对电阻比值的要求,这样,整个滤波器最终需要6个运放。
3 带通滤波器的电路级设计与仿真
3.1 运算放大器的设计与仿真
将有损积分器中运算放大器的单位增益频率记为wiop,为了将运放对滤波器高频响应的影响降至最低,wiop应该大于滤波器本身的单位增益频率wo。 其中:
 (11)
(11)
式(11)表明:wiop至少要为7.74 Grad/s(即1.232 GHz)。为留取一定的设计余度,取单位增益频率为2 GHz。有限的输出阻抗也是影响滤波器性能的1个重要因素[13-15]。在差分模式下,滤波器的最大输出阻抗为1 kΩ。为此,设计了1个增益为40 dB、单位增益频率为2 GHz、输出电阻为200 Ω的运算放大器。在该设计中,采用负跨导单元作为差分输入对的负载;采用电流镜放大器以改进频率响应,并利用源极跟随器作为输出缓冲级,整体电路如图5所示。
图6所示为所设计的运算放大器的频率响应。从图6可以看出:运算放大器的直流增益为39.3 dB,单位增益频率为1.985 GHz,满足上述设计要求。同时,在设计中也使用了优化设计的数控电阻衰减网络进行通带增益调谐,如图7所示。
3.2 滤波器的整体电路设计
图8所示为滤波器的电路图,各元件值如表3 所示。
表3 滤波器各元件参数
Table 3 Parameters of filter components
对图8所示电路进行仿真,结果如图9所示。其中,图9(a)所示为滤波器通带纹波特性,可以看出:通带增益约为0 dB,通带纹波为0.112 dB。通带纹波小,表明该滤波器在通带内表现出较好的通带性能。
从图9(b)和(c)可见:滤波器的下-3 dB频率和上-3 dB频率分别为156 kHz和259 MHz;从图9(d)和(e)可见:所设计的带通滤波器在频率为500 MHz和45.16dB。该滤波器具有较好的阻带特性,克服了传统的超宽带带通滤波器阻带较窄,不能有效抑制谐波的缺点。

图5 运算放大器电路
Fig.5 Circuit of op-amp

图6 运算放大器的频率响应
Fig.6 Frequency response of op-amp
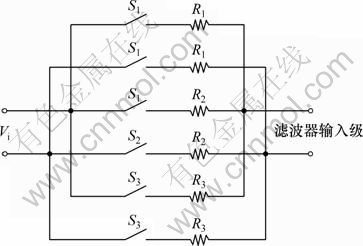
图7 滤波器通带增益调谐电路
Fig.7 Circuit for filter pass-band gain tuning

图8 滤波器电路
Fig.8 Circuit of filter
表4 带通滤波器电路仿真结果
Table 4 Circuit simulation results of band-pass filter

图10和图11所示分别为包含通带增益调谐电路的滤波器整体电路及其仿真波形。从图11可见:通过3位温度计码的控制,带通滤波器的通带增益可方便地调谐在0,5和10 dB,同时保持相同的频率特性;在频率为1 Hz处,滤波器对信号的衰减接近120 dB。在设计中,通过采用数控电阻通带增益调节电路使得滤波器通带增益很方便地调谐,改善了滤波器的性能。
上述所有仿真结果综合见表4。仿真结果表明:该滤波器具有宽通带、宽阻带、通带波纹小和阻带衰减快等优点。通带宽使得带内插损小,可以使能量更充分传输;宽阻带进一步增强频率选择性能,有效抑制高次谐波,从而使得带外抑制电平足够高,有效地降低干扰;阻带衰减快,表明频率选择性能突出。此外,该滤波器也具有结构简单,易于实现的优点,能够能得到推广,广泛采用。

图9 带通滤波器的频率响应
Fig.9 Frequency responses of band-pass filter

图10 包含通带增益调谐电路的带通滤波器
Fig.10 Band-pass filter with pass-band gain tuning circuit

图11 滤波器通带增益调谐仿真波形
Fig.11 Simulation results of filter pass-band gain tuning
4 结论
(1) 通过合理选择积分电阻, 有效地降低了有损积分器对运算放大器直流增益的要求,从而使得有损积分器的直流增益得到补偿。
(2) 采用数控电阻通带增益调节电路能有效地实现滤波器通带增益的调谐。
(3) 采用有源R-C方式和状态变量法设计了1个用于UWB接收端的带通滤波器。仿真结果表明,该滤波器具有宽通带、宽阻带、通带波纹小和阻带衰减快等特点,完全达到了UWB接收端滤波器性能指标要求。
参考文献:
[1] Xu H L, Yang L Q. Modeling and transceiver design for asymmetric UWB links with heterogeneous nodes[J]. IEEE Transactions on Communications, 2010, 58(6): 1834-1842.
[2] Joo Y J, Kim H S, Jung S Y. A tunable pulse generator for Sub-GHz UWB systems[C]//52nd IEEE International Midwest Symposium on Circuits and Systems. Cancun. Mexico, 2009: 292-296.
[3] HU Jun-ping, LIU Yong-chong, YANG Jie. The frequency domain method for UWB pulse design[C]//Proceedings of International Conference on Communication Software and Networks. Macau, China, 2009: 16-19.
[4] IEEE P802.15/268r3, Multi-band OFDM physical layer proposal for IEEE 802.15 task group 3a[S].
[5] Fan C C. Revision of Part 15 of the commission's rules regarding ultra-wideband transmission systems, Tech. ReP. ET-Docket, FCC-48[R]. Federal Communications Commission, 2002.
[6] YAO Bin-yan, ZHOU Yong-gang, CAO Qun-sheng, et al. Compact UWB bandpass filter with improved upper-stopband Performance[J]. IEEE Microwave and Wireless Components Letters, 2009, 19(1): 27-29.
[7] 姚望,李巍,李宁,等. 应用于OFDM超宽带系统中的0.18 μm Gm-C滤波器和可变增益放大器的设计[J]. 复旦大学学报: 自然科学版, 2008, 47(6): 755-762.
YAO Wang, LI Wei, LI Ning, et al. 0.18 μm Gm-C filter and VGA for OFDM UWB systems[J]. Journal of Fudan University: Natural Science, 2008, 47(6): 755-762.
[8] Yang G M, Geng R J, Huang J X. Ultra-wide-band(UWB) bandpass filter with hybrid quasi-lumped elements and defected ground structure[J]. IET Microwave, Antennas & Propagation, 2007, 1(3): 733-736.
[9] Hussein S, Jia S H. A novel ultra-wide band (UWB) bandpass filter(BPF) with pairs of transmission zeroes[J]. IEEE Microwave and Wireless Components Letters, 2007, 17(2): 121-123.
[10] Pal A, Kumar R, Mohan V, et al. Design of Chebyshev band pass filter[C]//International Conference on Emerging Trends in Electronic and Photonic Devices & Systems. Varanasi, India, 2009: 226-227.
[11] Inseon K, Kwisoo K, Jongsik L, et al. A modified generalized Chebyshev low-pass filter with wide stopband[J]. Microwave and Optical Technology Letters, 2009, 6(51): 1428-1431.
[12] Chun H C, Chi Y C. Wideband Chebyshev-response bandpass filter by cascading of cascadable 180° hybrid rings[C]// Proceedings of 2006 Asia Pacific Microwave Conference. Hsinchum, 2006: 1584-1587.
[13] Gong W B, Nan W. Design of a new high performance LC band-pass filter[J]. Telecommunication Engineering, 2008, 48(5): 112-114.
[14] Ching W T, Ming G C. A microstrip ultra-wideband bandpass filter with cascaded broadband bandpass and bandstop filters[J]. IEEE Transactions on Microwave Theory and Techniques, 2007, 55(11): 2412-2418.
[15] Gorur A, Karpuz C, Akpinar M. A reduced-size dual-mode bandpass filter with capacitively loaded open-loop arms[J]. IEEE Microw Wireless Compon Lett, 2003, 13(9): 385-387.
(编辑 陈灿华)
收稿日期:2011-03-05;修回日期:2011-06-02
基金项目:国家自然科学基金资助项目(60970137);国家重大专项(2008ZX03006-001,2009ZX03006-006);中国科学院知识创新工程项目(KGCX2-YW-120)
通信作者:王斌(1977-),男,山东文登人,博士研究生,高级工程师,从事信号与信息处理研究;电话:13651259577;E-mail:onlyou007@sohu.com