J. Cent. South Univ. (2016) 23: 181-188
DOI: 10.1007/s11771-016-3061-9
A novel hybrid algorithm based on a harmony search and artificial bee colony for solving a portfolio optimization problem using a mean-semi variance approach
Seyed Mohammad Seyedhosseini1, Mohammad Javad Esfahani2, Mehdi Ghaffari3
1.Department of Industrial Engineering, Iran University of Science and Technology, Tehran, Iran;
2. Young Researchers and Elite Club, Naragh Branch, Islamic Azad University, Naragh, Iran;
3. Department of Industrial Engineering, Naragh Branch, Islamic Azad University, Naragh, Iran
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: Portfolio selection is one of the major capital allocation and budgeting issues in financial management, and a variety of models have been presented for optimal selection. Semi-variance is usually considered as a risk factor in drawing up an efficient frontier and the optimal portfolio. Since semi-variance offers a better estimation of the actual risk portfolio, it was used as a measure to approximate the risk of investment in this work. The optimal portfolio selection is one of the non-deterministic polynomial (NP)-hard problems that have not been presented in an exact algorithm, which can solve this problem in a polynomial time. Meta-heuristic algorithms are usually used to solve such problems. a novel hybrid harmony search and artificial bee colony algorithm and its application were introduced in order to draw efficient frontier portfolios. Computational results show that this algorithm is more successful than the harmony search method and genetic algorithm. In addition, it is more accurate in finding optimal solutions at all levels of risk and return.
Key words: portfolio optimizations; mean-variance model; mean semi-variance model; harmony search and artificial bee colony; efficient frontier
1 Introduction
A harmony search (HS) is a new meta-heuristic algorithm developed by Geem et al [1] and inspired by the natural musical performance process that occurs when a musician searches for a state of harmony. A musical instrument in improvisation corresponds to a decision variable in optimization: its pitch range corresponds to a value range, and a harmony corresponds to a solution vector. In the HS algorithm, a musician plays a pitch that is essentially based on one of three factors: randomness, experience, and variation of experience. The HS algorithm imposes fewer mathematical requirements compared to other meta-heuristics and can easily be adapted to solve various types of engineering optimization problems. Furthermore, numerical comparisons have shown that the evolution of the HS algorithm is faster than that of the genetic algorithm (GA) [2]. Therefore, the HS algorithm has captured a great deal of attention, and has successfully been applied to solve a wide range of practical optimization problems [3-8]. This algorithm is effective in identifying the high performance regions of a solution space within a reasonable time; however, it is not efficient in performing a local search in numerical optimization applications [3].
The artificial bee colony (ABC) algorithm is a new collective intelligence technique inspired by the intelligent exploratory behavior of honey bees. In this algorithm, an ABC consists of three groups of bees: worker bees, spectators, and scouts. A bee waiting on the dance area to select a food source for bees and wasps is called a spectator bee, and a bee that goes to previously visited food is called a worker bee. The scout bee conducts random searches to discover new food sources. The position of a food source represents a possible solution to the optimization problem and the nectar amount of a food source quality (fitness) is the associated solution [9].
thanks to the pioneering work of Markowitz [10], the development of modern portfolio theory began in 1952, and this started a new branch of financial economics, addressing the optimal allocation of financial assets. Every investor decides which assets to invest depending on personal risk tolerance and objectives. Some investors (mostly speculators) accept a very high risk for the attractive prospect of greater return. Others (mostly conservative and institutional investors) tolerate lower levels of risk and prefer less volatile portfolios. Mean-variance (MV) optimization searches for the optimal investment allocation, considering the trade-off between the risk (represented by the variance of returns) and the expected (mean) return of the chosen assets in a portfolio. The optimal portfolio lies in an efficient frontier, which shows the maximum return possible for given levels of risk. Alternatively, the MV optimization can be set to minimize the portfolio variance for a given expected target return [11].
In 1996, on the basis of their research, Jia and Dyer [12] pointed out the fact that these conditions rarely exist in real-world problems. Therefore, the MV objective function considering other risk criteria cannot be sufficiently appropriate. However, other risk criteria that consider the preferences of the investors in different conditions could be more suitable. Moreover, in real- world problems, investors increase some constraints of their optimization model, such as the size of the portfolio, the minimum and maximum amount of investment in an asset. Such constraints may create a nonlinear integer programming model, which may be more difficult to solve than the original problem.
Many researchers have attempted to find the global optimum for such problems, but the exact solution methods are not successful. Therefore, they have tried meta-heuristic methods, such as the GA and the HS algorithm, in order to solve the portfolio optimization problem [13].
Xia et al [14] proposed a model for portfolio selection in which expected returns were ranked, while Crama and Schyns [15] tested the use of a mixed integer quadratic model to solve a complex portfolio selection problem. Deng et al [16] subsequently applied the New Mini Max approach to model those portfolio selection problems that have random uncertainty in the input data. Hao et al [17] applied the GA to study new examples of the MV model based on Markowitz’s theory for portfolio selection problems with random investment returns. It was found that the asymmetric returns changed the variance into an inefficient criterion for risk assessment.
Numerous researchers have worked on properties and calculations of semi-variance and hajne has improved the mean semi-variance models. Fine et al [18] examined such models in various states, presented three models based on minimizing the risk using the criterion of semi variance and discussed the evaluation of the performance of the mean-semi variance model under uncertainty by entering the fuzzy return. Ceria [19] showed that consideration of risks as a factor that does not impose a fee on portfolio selection led to an ineffective and in some cases illogical solution. They emphasized that in models aimed at maximizing returns and reducing risk, the risk aversion coefficient must have considerable value. The weighted upper limits on the constraints of portfolio models were set by Saxena et al [20] who did not consider the risk of the portfolio, as calculated from previous data, and took advantage of a scenario-based approach. They pointed out that use of weighted constraints in the MV model revealed the systematic weight of investment risk in portfolio selection, which is not possible in the normal MV model.
In 2011, GharAkhani and Sadjadi [21] applied multi-period robust optimization and stochastic programming to determine the rate of return in future planning, and used data simulation in order to evaluate the performance of their proposed model. They subsequently introduced a new approach with uncertain data in portfolio modeling, and analyzed this using a different robust method. They solved this formulation with the help of GA, and compared it with various benchmarks [22]. A comprehensive review of the 60-year history of portfolio optimization was presented and analyzed by Kolm et al [23].
Hybrid algorithms have been used by researchers to find the optimized portfolio using the combination of evolutionary algorithms, along with other local search algorithms. However, the problem is that in algorithms that simultaneously use an evolutionary algorithm as a global search, the local search algorithm runs as another algorithm on the entire population with the aim of finding the best solution, which results in a reduction of the efficiency of this algorithm.
The present study aims to identify the efficient frontier of investment and to investigate the possibility of identifying the optimum portfolio formation by meta-heuristic algorithms based on the population, using a hybrid algorithm harmony search with an artificial bee colony (HHSABC).
2 Portfolio selection constraints
The total assets in a portfolio are often considered with an upper limit. If the variable zi is a 0, 1 variable that identifies selecting or deselecting of stock, then i is in the portfolio, n indicates the number of active firms in the stock market, and K represents the upper limit of investment. The constraint is shown as follows:
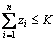 (1)
(1)
This constraint is imposed in order to facilitate portfolio management and reduce the costs of the latter. This relationship was introduced by Schaerf [24] and then Kellerer and Mariginer [25]. In addition, Maringer [26] and Chiam et al [27] added a lower limit to this constraint and proposed the following relationship for the number of selected stocks:
 (2)
(2)
However, in most other studies, for example, ARM NANZAS and Lozano [28] and Soleimani et al [29] converted this relationship to the equation shown below:
NANZAS and Lozano [28] and Soleimani et al [29] converted this relationship to the equation shown below:
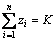 (3)
(3)
Minimum and maximum allowable constraints can then be named for each stock in the selected portfolio. Fernandez and Gomez [13] introduced an upper limit constraint to avoid exceeding the specific asset ratio. The lower limit constraint was set so as not to allow the management costs to exceed other assets. These constraints may be required on the basis of investment laws and regulations or trading costs. The following relationship shows the constraint for the share i:
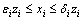 (4)
(4)
In relationship (4), xi represents the amount of investment in share i, εi and δi are the lower and upper limits of investment, respectively.
3 Portfolio optimization problem
Risk and return of capital assets are two important factors in investment. Most investors are looking to maximize their returns at a certain level of risk, or minimize their risk at a certain level of return. The Markowitz MV model shows that formation of a financial assets portfolio creates the possibility of reducing risk at a certain level of return. This possibility occurs because of the lack of perfect correlation among different financial returns. People make investments on the basis of their expected utility and in the hope of more consumption in future, ignoring today’s consumption. The utility function of each investor is determined by his or her preferences, and these will not necessarily be identical to those of other investors.
Risk and return are the criteria that determine the value of an investor’s utility of a selected portfolio. Optimal portfolio selection often involves a conflict between risk and return, and if the portfolio has a greater risk, the investors will expect to receive a higher return. Identification of the efficient frontier of the portfolio will allow investors to earn the highest expected return from their investments on the basis of their utility function and their risk aversion and risk-taking. investors select a point on the efficient frontier on the basis of their attitude to risk and risk aversion, and set the composition of their portfolio with the objective of maximizing return and minimizing risk [30].
Markowitz [30] presented the problem using quadratic programming, with the objective of minimizing the variance of investments and the condition that the expected return is a constant value. The main assumption of this model is that all investors are risk-averse. It also has a functional limitation based on the fact that the total weight of the investment should be equal to one. In addition, the weight of each investment in the portfolio must be a non-negative real number.
Fernandez and Gomez [13] then modified the Markowitz model, adding the upper limit and lower limit constraints. The modified model is as follows:
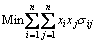 (5)
(5)
st.
 (6)
(6)
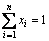
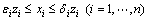 (7)
(7)
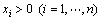 (8)
(8)
 (9)
(9)
Achievement of a certain efficiency of return is one of the requirements of the above model, but this is not possible in some cases. Therefore, in addition to the objective function to minimize risk, maximization of efficiency is also added, and the model of Fernandez and Gomez [13] is revised, as follows:
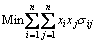 (10)
(10)
st.
 (11)
(11)
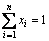
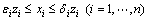 (12)
(12)
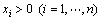 (13)
(13)
 (14)
(14)
In the above model, λ is a parameter with a value that changes in the interval [0, 1], such that when λ0= total value of weight is assigned to the return and, without regard to risk, the portfolio with the highest return will be selected, and when λ=1, the total amount of weight is assigned to risk, without regard to return, and the portfolio with the lowest risk will be selected. In the interval (0, 1), the portfolios that consider both risks and returns are optimized. In other words, with the increase in λ, the objective function of reducing risk becomes more important, and the coefficient of maximizing return in the objective function (1-λ) will simultaneously be reduced. εi and di are the lower and upper limits of variable i (the ratio of share I in the portfolio), respectively, zi is a binary variable that takes the value 1 when the share i is in the portfolio, and xi indicates the amount of investment in share i.
The above model, called the semi variance model, is generally used in portfolio optimization. It has optimized the model introduced by Fernandez and Gomez [13] in that instead of using variance of the risk as a factor, semi variance is used and defined as follows:

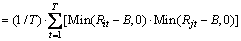 (15)
(15)
where E{} states the expected value, B is the return under comparison, and Rit indicates the return of the share i, in period t. If the mean return (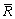 ) is replaced by the objective return (B) in the above formula, semi covariance is obtained. The final mean semi variance model is as follows:
) is replaced by the objective return (B) in the above formula, semi covariance is obtained. The final mean semi variance model is as follows:
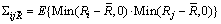
 (16)
(16)
After solving the portfolio optimization problem, considering different returns of investments and determining optimal weights, a graph similar to Fig. 1 is obtained.
5 Hybrid harmony search with artificial bee colony algorithm
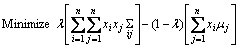 (17)
(17)

Fig. 1 An example of an efficient frontier for an investment
Subject to 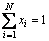 (18)
(18)
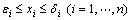 (19)
(19)
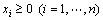 (20)
(20)
In order to enhance the accuracy and speed of convergence of a harmony search, a hybrid harmony search algorithm combining an ABC is proposed; the ABC algorithm is used to improve the harmony memory (HM). The general steps of the HHSABC algorithm are displayed in Figs. 1 and 2. First, as can be observed, the parameters of the algorithm are determined, after which a series of random responses are generated and located in the HM. Then, in step 3, the improvements to the solutions are achieved with the use of the ABC algorithm, as shown in Fig. 3. In this step, any harmony (solution) can be randomly changed. If the improvement has been made, the solution is replaced by the previous solution; otherwise the process will be repeated. If the solution is changed for a limited random number and no improvement is made, it should be eliminated from the HM set and substituted by another random solution.
As can be seen, in the steps of hybrid algorithm, the values of the decision variables are determined randomly in such circumstances, and all constraints of the model may not satisfy.
When meta-heuristic methods are used to solve optimization problems, constraints are often considered as penalty functions in the fitness function. In this work, in an approach similar to that used by Cura [31], some sub-algorithms are considered with regard to the constraint satisfaction problem. In order to set the constraint for the number of selected stock, the variable 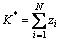 and the collection Q are defined. Q is the collection that contains the solution vector x, and K* indicates the number of shares in the collection Q. If it is assumed that K is the number of desirable assets in the portfolio, in the case K*
and the collection Q are defined. Q is the collection that contains the solution vector x, and K* indicates the number of shares in the collection Q. If it is assumed that K is the number of desirable assets in the portfolio, in the case K* to Q, and when K*>K, some shares must be reduced, such that equality is established (K*=K). In order to make decisions regarding which shares should be added or subtracted from set Q, the relative effect of each share on the fitness function (ci) is measured. Shares or assets with higher relative effects on the fitness function have a higher priority for addition to the collection, and vice versa, the shares with a lower effect on the fitness function are the priority for removal from the collection Q. The calculation of ci is based on several formulas. First, using the following relationship, the value of ci is obtained for the share i:
 (25)
(25)
 (26)
(26)
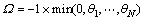 (27)
(27)
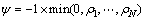 (28)
(28)
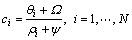 (29)
(29)
Therefore, in the case K*>K, the share with the minimum value of c is deleted from the collection and in the case K*i is the proportion of investment in share i. The summation of xi (i=1, …, n) for the shares in the collection Q must be equal to one. If χ is the sum of xi (i=1, …, n), using the conversion of xi= xi/χ for all shares in Q, the constraint of weights being equal to 1 is satisfied.
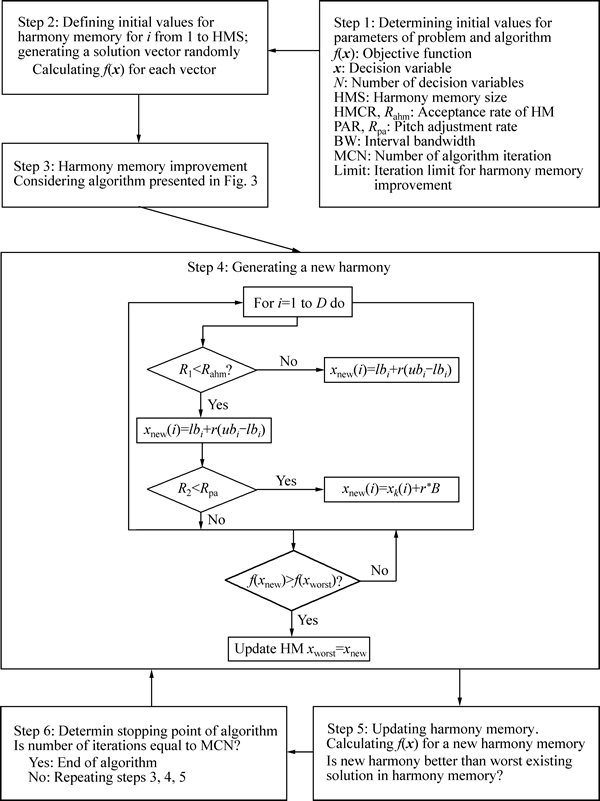
Fig. 2 An overview of HHSABC algorithm
Lower and upper limits of the constraint for investment (inequality εi≤xi≤di) should also be established for the shares in collection Q. To set this constraint, variables ti=di-xi and ei=xi-εi are defined for the shares in collection Q. d* and ε* are the summations of ti and ei, respectively. η is the sum of -1×ti for those ti that ti <0; f is the sum of (-1×ei) such that ei<0. If the amount of an investment goes higher than the upper limit or moves below the existing lower limit, the corresponding constraint is established on the basis of the following equation:
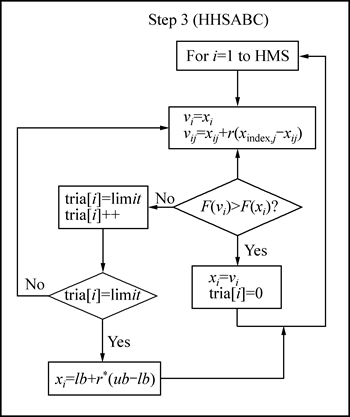
Fig. 3 Step 3 of HHSABC algorithm
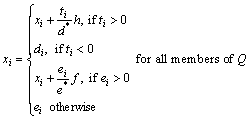
6 Case study
The statistical population consists of all firms in the Tehran Stock Exchange in 1931. To access the data required for processing the hypotheses of this research, the documents that firms provide to the stock exchange are used. To provide a solution, the information relating to 102 active companies in the Tehran Stock Exchange is listed in 17 categories. In this work, the mean-semi variance model is used to draw up the efficient frontier of investment. In order to evaluate the performance of the hybrid algorithm, HHSABC is used.
The parameters of the hybrid algorithm are as follows:
HM size: the number of solution vectors in HM that is usually considered equal to 25.
HM consideration rate: the probability of choosing each component of the new harmony (new solution vector) from the collection of existing vectors in the HM, which is considered equal to 0.9 in the present study.
Pitch adjustment rate (PAR): a new harmony component selected from HM should be examined to adjust the pace.
The component of the new solution vector with the probability of PAR requires an adjustment to its pace rate, and with the probability of (1-PAR) its pace rate remains unchanged. In this algorithm, the PAR is considered equal to 0.3.
Bandwidth (bw): If it is necessary to set the pace of a new harmony, the maximum possible change in value will be equal to bw. This is an arbitrary distance that is usually determined on the basis of the personal experience of the programmer. In this algorithm, bw is considered equal to 0.001.
Undesirable constraint (limit) is considered equal to 0.3.
The number of algorithm iterations: it is defined as a condition to end the algorithm. In this algorithm, the condition of ending based on the number of iterations is considered equal to 500.
The following values can be considered for the parameters of the mean-semi variance model:
Constraint of the number of shares (K): the constraint related to those shares that the investor is willing to maintain in his or her portfolio. In this work, the values of this parameter are considered to be 3, 5, 10, and 15, respectively.
Coefficient of risk aversion (λ): a number in the interval [0, 1] that is used for tracking the efficient frontier of the risk-aversion coefficient. In order to draw the efficient frontier in each iteration of the algorithm, the coefficient of risk aversion varies by 0.1 unit. When it is equal to 0, the objective of the model is to maximize the return regardless of the risk, and when the value of risk aversion is equal to 1, the objective of the model is to minimize the risk regardless of the return.
The lower limit (εk) and upper limit (dk) for each decision variable: if it is supposed to invest in a share, the maximum and minimum values of the ratio of capital investment in that share can be added to this problem. In the present study, the maximum and minimum values of the ratio of investment are considered to be 1 and 0.0001, respectively, for all selected assets.
Finally, running the algorithms HS, GA, and the hybrid HHSABC algorithm, using MATLAB software under different restrictions on the number of shares (k), the efficient frontiers of these three algorithms are calculated and compared, as shown in Figs. 4-7.
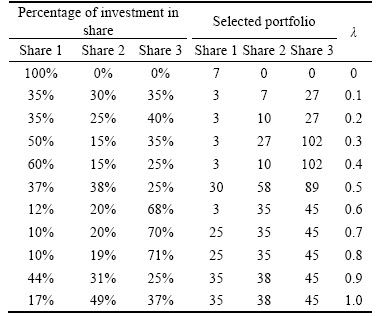
In different cases for each algorithm, a particular portfolio is obtained as the output that would determine the companies that should invest, and how much should be invested. Choosing to invest the percentage of investment in each company depends on the coefficient of risk aversion. When this ratio is equal to 0, the company with the highest return is selected and when this ratio is 1, the company with a minimum value of investment risk is selected. For example, the selected portfolio in the case of K=3 is specified in Tables 1 and 2.
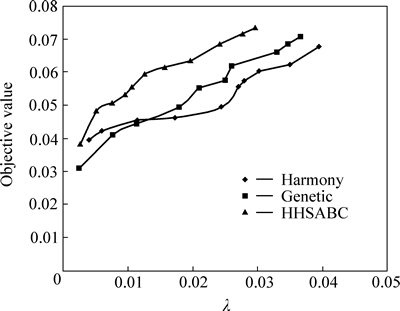
Fig. 4 efficient frontier of mean-semi variance for a portfolio of 3 shares

Fig. 5 efficient frontier of mean-variance for a portfolio of 15 shares

Fig. 6 efficient frontier mean-variance for a portfolio of 15 shares
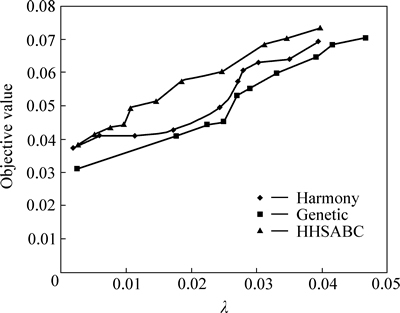
Fig. 7 efficient frontier of mean-variance for a portfolio of 10 shares
Table 1 Comparison of results of genetic algorithm, harmony search algorithm, and hybrid harmony search and artificial bee colony for mean-variance model (three shares)
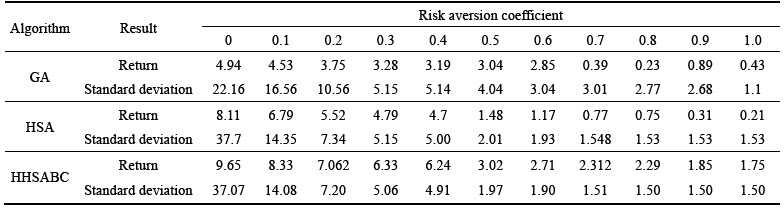
Table 2 Selected portfolio and percentage of investment (three shares)
7 Conclusions
a new hybrid algorithm called HHSABC search is presented. Since semi variance is a more appropriate estimator of portfolio risk than variance, the Markowitz mean-semi variance model is proposed. Finally, the efficient frontiers obtained by the hybrid algorithm, HS algorithm, and GA are compared to evaluate the efficiency and accuracy of the hybrid algorithm. The results indicate that the latter is relatively more efficient than the two other algorithms at all levels of risk, and offers a good approximation of the efficient frontier of investment. Other models, such as the mean-absolute value model or the mean-variance-skewness model, can be used in further research in order to calculate the risk of capital investment and draw the efficient frontier.
References
[1] GEEM Z W, KIM J H, LOGANATHAN G V. A new heuristic optimization algorithm: harmony search [J]. Simulations, 2001, 76: 60-68.
[2] MAHDAVI M, FESANGHARY M, DAMANGIR E. An improved harmony search algorithm for solving optimization problems [J]. Appl Math Comput, 2007, 188: 1567-1579.
[3] LEE K S, GEEM Z W, LEE S H, BAE K-W. The harmony search heuristic algorithm for discrete structural optimization [J]. Eng Optim, 2005, 37: 663-684.
[4] GEEM Z W. Optimal cost design of water distribution networks using harmony search [J]. Eng Optim, 2006, 38: 259-280.
[5] GEEM Z W. Harmony search algorithm for solving Sudoku [C]// Proceedings 11th International Conference. Springer, Heidelberg, 2007: 371-378.
[6] FORSATI R, HAGHIGHAT A T, MAHDAVI M. Harmony search based algorithms for bandwidth-delay-constrained least-cost multicast routing [J]. Comput Commun, 2008, 31: 2505-2519.
[7] CYLAN H, HALDENBILEN S, HALDENBILEN S, BASKAN O. Transport energy modeling with meta-heuristic harmony search algorithm, an application to Turkey [J]. Energy Policy, 2008: 2527-2535.
[8] SAKA M P, ERDAL F. Harmony search based algorithm for the optimum design of grillage systems to LRFD-AISC [J]. Struct Multidiscip Optim, 2009, 38: 25-41.
[9] WU B, QIAN C, NI W, FAN S. Hybrid harmony search and artificial bee colony algorithm for global optimization problems [J]. Computers & Mathematics with Applications, 2012, 64(8): 2621-2634.
[10] MARKOWITZ H. Portfolio Selection [J]. Journal of Finance, 1952, 7(1): 77-91.
[11] XUE Q, WANG Z, LIU S, ZHAO D. An improved portfolio optimization model for oil and gas investment selection [J]. Pet Sci, 2014, 11: 181-188.
[12] JIA J, DYER J S. A standard measure of risk and risk-value models [J]. Management Science,1996, 42(12): 1691-1705.
[13] FERNANDEZ A, GOMEZ S. Portfolio selection using neural networks [J]. Computers & Operations Research, 2007, 34: 1177-1191.
[14] XIA Y, LIU B, WANG S, LAI K. A model for portfolio selection with order of expected returns [J]. Computers and Operations Research, 2000, 27: 409-422.
[15] CRAMA Y, SCHYNS M. Simulated annealing for complex portfolio selection problems [J]. European Journal of Operational Research, 2003, 150: 546-571.
[16] DENG X, LI Z, WANG S. A minimax portfolio selection strategy with equilibrium [J]. European Journal of Operational Research, 2005, 166: 278-292.
[17] HAO F F, LIU, Y K. Mean variance models for portfolio selection with fuzzy random returns [J]. Springer: J Appl Math Comput, 2007, 30: 9-38
[18] FINE J P, JIANG, H, CHAPPELL R. On semi-competing risks data [J]. Biometrika,2001, 88(4): 907-919.
[19] CERIA S. To optimize or not to optimize: Is that the question? [M]// The oxford handbook of quantitative asset management. New York: Oxford University Press, 2012: 50-64.
[20] SAXENA A, MARTIN C, STUBBS R A. Aligning alpha and risk factors, a panacea to factor alignment problems? [R]. Axioma Inc. 2012.
[21] GHARAKHANI M, SADJADI S. A new approach to robust modeling of the multi-period portfolio problem [J].African Journal of Business Management, 2011, 5(23): 9998-10006.
[22] SADJADI S J, GHARAKANI M, SAFARI E. Robust optimization framework for cardinality constrained portfolio problem [J].Applied Soft Computing,2012, 12(1): 91-99.
[23] KOLM P N, T T
T NC
NC R, FABOZZI F J. 60 years of portfolio optimization: Practical challenges and current trends [J]. European Journal of Operational Research,2014, 234(2): 356-371.
R, FABOZZI F J. 60 years of portfolio optimization: Practical challenges and current trends [J]. European Journal of Operational Research,2014, 234(2): 356-371.
[24] SCHAERF A. Local search techniques for constrained portfolio selection problems [J]. Computational Economics, 2002, 20(3): 177-190.
[25] KELLERER H, MARINGER D. Optimization of cardinality constrained portfolios with a hybrid local search algorithm [J]. OR Spectrum, 2003, 25(4): 481-495.
[26] MARINGER D. Portfolio management with heuristic optimization [J]. IEEE Computational Intelligence Magazine,2008, 3(4):31-34..
[27] CHIAM S C, TAN K C, AL MAMUM A. Evolutionary multi- objective portfolio optimization in practical context [J]. International Journal of Automation and Computing, 2008, 5(1): 67-80.
[28] ARM NANZAS R, LOZAN J A. A multiobjective approach to the portfolio optimization problem [C]// Proceedings of the IEEE Congress on Evolutionary Computation. Piscataway, USA: IEEE, 2005: 1388-1395.
NANZAS R, LOZAN J A. A multiobjective approach to the portfolio optimization problem [C]// Proceedings of the IEEE Congress on Evolutionary Computation. Piscataway, USA: IEEE, 2005: 1388-1395.
[29] SOLEIMANI H, GOLMAKANI H, SALIMI M H. Markowitz based portfolio selection with minimum transaction lots, cardinality constraints and regarding sector capitalization using genetic algorithm [J]. Expert Systems with Applications, 2009, 36: 5058-5063.
[30] MARKOWITZ H. Portfolio Selection. Efficient diversification of Investments [M]. New York: John Wiley & Sons, 1959.
[31] CURA T. Particle swarm optimization approach to portfolio optimization [J]. Nonlinear Analysis: Real World Applications, 2009, 10: 2396-2406.
(Edited by FANG Jing-hua)
Received date: 2014-08-25; Accepted date: 2014-12-24
Corresponding author: Mohammad Javad Esfahani, PhD Candidate;Tel: +98-9187654910;E-mail: mjesfehani2000@gmail.com