文章编号：1004-0609(2007)02-0216-06

MoSi₂价电子结构分析及结合能计算

彭  可¹，易茂中¹，陶辉锦²，冉丽萍¹

(1. 中南大学 粉末冶金国家重点实验室，长沙 410083;

2. 中南大学 材料科学与工程学院，长沙 410083)

摘  要：根据固体与分子经验电子理论，通过键距差(BLD)方法，计算了金属间化合物MoSi₂的价电子结构和理论结合能。结果表明，MoSi₂理论结合能为1 677.1 kJ/mol，与实验值吻合。由于Si原子偏移，沿〈001〉方向分布的Si—Si原子键共价电子数最多，n_D=0.402 04。MoSi₂晶体中含有较高密度的晶格电子，使MoSi₂具有良好的导电性。MoSi₂晶体中键络分布不均匀性是导致晶体脆性的主要原因。

关键词：二硅化钼；价电子；结合能；脆性

中图分类号：TG 148　　     文献标识码：A

Valence electronic structure analysis and

cohesive energy calculation of MoSi₂

PENG Ke¹, YI Mao-zhong¹, TAO Hui-jin², RAN Li-ping¹

(1. State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China;

2. School of Materials Science and Engineering, Central South University, Changsha 410083, China)

Abstract: According to the empirical electron theory of solid and molecule, the valence electron structure and theoretical cohesive energy of MoSi₂ were calculated by the BLD method. The results show that the theoretical cohesive energy of MoSi₂ is 1 677.1 kJ/mol, which agrees well with the experimental data. Because of a shift in Si positions, the valence electrons between Si—Si atoms along <001> direction are the most (n_D = 0.402 04). There are lattice electrons with higher densities in MoSi₂, which accounts for the good conductivity of MoSi₂. Also, it is speculated that the brittleness of MoSi₂ can be explained primarily by a heterogeneity of bond distribution.

Key words: molybdenum disilicide; valence electron; cohesive energy; brittleness

金属间化合物MoSi₂以其高熔点(2 030 ℃)、较低密度(6.24 g/cm³)、优异的高温抗氧化性和耐蚀性、良好的导电导热性而成为新型高温结构材料和微电子领域的研究热点之一^[1-2]。但MoSi₂在900 ℃以下断裂韧性仅为2~4 MPa?m^1/2，低温脆性妨碍了它的实际应用。从价电子结构的层次去理解MoSi₂的一些重要性能，对于有效改善材料的性能和更好的进行材料设计具有重要意义。

MoSi₂是一种道尔顿型金属间化合物，1 900 ℃以下为C11_b型体心正方结构（如图1所示），空间群为I4/mmm，Mo原子占据2a(0, 0, 0)位，Si原子占据4e(0, 0, u)位。MoSi₂的理论研究已有较多工作涉及，以前研究认为，尽管沿<001>方向Mo、Si原子层并非交替堆垛，但在(001)面的面间距相等，即u=c/3^[3]。但是，通过X射线粉末衍射的Rietveld精修^[4]和单晶体衍射法^[5]测定MoSi₂晶体结构，发现在<001>方向上Si原子向相邻的Si原子偏移，偏离c/3位置。Bhattacharyya等^[6]利用自洽赝势电子理论计算了MoSi₂的电子结构和理论结合能，发现当Si原子偏离c/3位置时，MoSi₂总能量减小，但理论结合能与实验值存在较大误差，且没有确切给出MoSi₂金属间化合物金属键与共价键含量。而应用固体与分子经验电子理论，可直接讨论金属间化合物中原子所处价态并半定量给出原子键中共价键的相对贡献。周飞^[7]用固体与分子经验电子理论分析了MoSi₂的价电子结构，但没有考虑Si原子的偏移对实验键距的影响，而实验键距是确定原子杂化状态的重要参数。

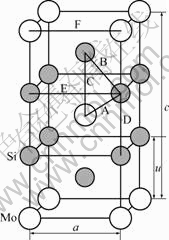
图1  C11_b型MoSi₂的晶体结构

Fig.1  Crystal structure of MoSi₂ with C11_b structure

本文作者利用固体与分子经验电子理论，考虑了Si原子的偏移，对MoSi₂进行价电子结构分析，并用徐万东等^[8]提出的过渡金属化合物晶体结合能公式计算了MoSi₂的理论结合能，分析了Si原子偏移对价电子结构的影响和MoSi₂晶体脆性产生的主要原因。

1  理论键距的计算

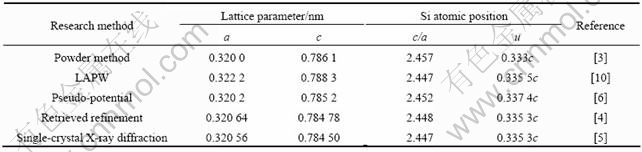
固体与分子经验电子理论的核心是原子的杂化状态和键距差法(Bond Length Difference, BLD)。键距差法利用已知的晶格参数求得晶体中各原子的杂化和它们之间的共价电子分布，建立起晶体或分子的价电子结构^[9]。进行BLD计算的前提条件是必须知道其晶体结构，即要知道晶体结构类型、晶格常数和原子坐标参数的具体数值。从实验和理论计算获得的MoSi₂晶胞结构参数列于表1。本文作者采用文献[5]的晶胞结构参数来计算实验键距，即a=0.320 56 nm，c＝0.78450 nm，u=0.263 03 nm。

表1  从实验和理论计算获得的MoSi₂晶胞结构参数

Table 1  Structure parameters of MoSi₂ obtained from experiments and calculations

利用式(1)可计算原子间键距。

通过分析MoSi₂的晶体结构，位于中心结点的Mo原子和8个顶角的Mo原子为同类原子，位于体心的Si原子和其他结点位置的Si原子也为同类原子。所以，在MoSi₂的C11_b相结构具有6种不可忽略的键，如图1所示，计算各键的实验键距为

根据公式I_a=I_MI_SI_K^[8]可求出各键的等同键数为

I_A＝32，I_B＝16，I_C＝8，I_D＝4，I_E＝16，I_F＝8。

EET理论在计算晶体电子结构时采用键距差(BLD)法。

由键距方程可知：

因此任两键键距差为

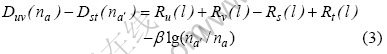
令，则得到一个包含N-1个方程的方程组，称为r_α方程。

计算MoSi₂的价电子结构时将各键实验键距D(n_α)和单键半距R_Mo(l)、R_Si(l)代入r_α方程。其中，R_Mo(l)、R_Si(l)分别由Mo和Si的杂化表提供。取β＝0.060，由r_α方程计算得到各r_α值。

将r_α值代入n_α方程：，求出n_α值。根据EET理论，将所得n_α代入理论键距方程，计算理论键距。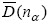

计算所得符合键距差条件的杂阶组合的n_α的最大值为0.3~0.7，表明β值选取正确。

2  键能和理论结合能的计算

Mo—Mo和Si—Si原子间共价键键能可用式(4)计算：

Mo－Si原子间共价键键能可用式(5)计算，

过渡金属化合物晶体结合能经验理论计算公式如下^[8]：

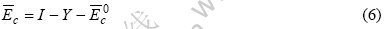
式中　I是在晶体中不同种类的原子间相互成键时，多为键提供共价电子的原子的类离化能；Y是当不同种类原子成键时，少提供共价电子的原子的类亲和能。

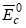是与元素晶体类似的晶体结合能，其具体表达式为

3  MoSi₂的价电子结构计算结果

根据Mo和Si的杂化表, 将有关数据代入经验键距公式和过渡金属化合物晶体结合能经验理论计算公式，计算出各键距理论值和MoSi₂的理论结合能，再结合实验键距及结合能实验值确定最佳组合杂阶态^{[9, 12-13]}，即可确定Mo和Si所在杂阶。

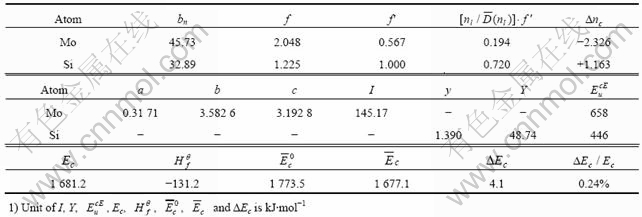
通过编程计算，MoSi₂晶体的Mo处于丙种杂化第3阶，Si处于第1阶。利用式(4)和(5)计算各键键能。计算过程中所需的Mo原子和Si原子的杂化状态参数如表2所示。表中σ表示杂阶的顺序，R(l)表示单键半距；l、m、n和l′、m′、n′分别表示原子杂化h态和t态中的s、p、d共价电子数和晶格电子数；τ、τ′是参数，当s电子是共价电子时，τ=τ′=1，当s电子是晶格电子时，τ=τ′=0；C_hσ与C_tσ分别表示第σ杂阶中h态和t态的成分；n_Tσ、n_lσ、n_cσ分别表示第σ杂阶的总价电子数、晶格电子数和共价电子数。计算得到的MoSi₂的价电子结构和各键键能值列于表3，MoSi₂晶体结合能计算结果列于表4。MoSi₂晶体理论结合能为1 677.1 kJ/mol，与MoSi₂结合能实验值(1 681.2 kJ/mol^[6])仅相差0.24%，比用自洽赝势电子理论计算的结果(=1 847.8 kJ/mol^[6])要好得多。

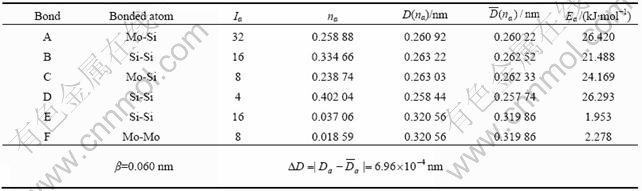
表2  Mo和Si原子杂化状态参数

Table 2  Hybridization state parameters of Mo and Si atoms

表3  MoSi₂价电子结构

Table 3  Valence electron structure of MoSi₂

4  分析与讨论

4.1  Si原子偏移对共价电子的影响

余氏分子经验电子理论(EET)认为：共价电子对是原子间结合的主要基础，原子间结合力的大小取决于共价电子数。两原子之间结合键的共价电子数越多，原子间结合力越大。由于Si原子从u=c/3的位置偏移到u=0.335 3c的位置，使得沿c轴方向的分布的最近邻Si—Si原子键（D键）键距最短。由表3可见，D键上共价电子对数最多，n_D=0.402 04，其键能仅次于A键，E_D=26.293 kJ/mol。Harad等^[4]利用离散变分Xα原子簇方法计算出，由于Si原子的偏移，Si—Si原子结合键之间的电子密度增加，键能增加，该键的电子密度最高，具有强的共价相互作用。用最大熵值法(MEM)^[14]可以得到相同的结论。

4.2  MoSi₂熔点与价电子结构的关系

MoSi₂具有高熔点(2 030 ℃)，在氧化性气氛下能长期使用到1 600 ℃而不致破坏。其高熔点的成因可以从其价电子结构特点去加以分析。根据EET理论^[10]，晶体熔化只需使晶体中维持原子呈三维周期排列的主干键络破坏。随着温度升高，固态晶体的原子热振动振幅增加。当温度升至熔化温度时，原子热振动振幅大到足以破坏近邻原子之间的结合键，即原子振动动能达到主干键络的键能，主干键络结合被破坏，晶体发生熔化。根据键能计算结果，在MoSi₂晶体中，沿<331>位向分布的A键的键能最大，E_A＝26.420 kJ/mol,且有32个等同键数，是晶体中维持原子呈三维周期排列的主干键络。要使MoSi₂相熔化，必须破坏A键，需要较高能量，因而宏观上就表现为高熔点。

4.3  MoSi₂电阻率与价电子结构的关系

按EET理论，晶格电子数目的增加意味着晶体导电性的增加。由文献[9, 15]，纯Mo晶体的杂阶为A3，Si的杂阶为4。在Mo与Si反应前，Mo原子有 1.238 6个晶格电子，具有较好的导电性；Si原子在4阶形成sp³共价键，由于较强的共价键，其电子不易脱离晶格的束缚而参与导电，仅有0.336个晶格电子。由表2可知，Mo与Si反应形成MoSi₂后，MoSi₂晶体Mo原子处于丙种杂化第3阶，有0.949 2个晶格电子；而Si原子处于第1阶，有2个晶格电子。虽然Mo原子的晶格电子数有所减少，但Si原子的晶格电子数大幅增加，MoSi₂的平均晶格电子数为(n_lMo+2n_lSi)/3= (0.949 2+2×2)/3=1.649 7，其晶格电子数大于反应前参与导电的晶格电子数。由此可以推断，MoSi₂晶体具有较好的导电性。实验结果表明，其室温电阻率为21.5 μW?cm ^[16]。EET理论计算与实验结果吻合。

表4  MoSi₂晶体结合能计算数据及结果

Table 4  Calculation data and results of Cohesive Energy of MoSi₂

4.4  MoSi₂价电子结构与脆性

尽管影响脆性的因素是多方面的，但某些合金(特别是金属间化合物)的脆性可与其价电子结构特点直接联系^[17-18]。MoSi₂晶胞空间键络在(100)面上的投影如图2所示。由计算结果可知MoSi₂的(100)面之间分布着最强键A键和较强键B键，分别有32和16个等同键数；而(100)面上各键共价电子数相对较少，虽然次强键D键和较强键C键分布其上，但等同键数分别为4和8，且分布不对称，而其他键的键强又很弱。因此，C11_b型晶体对称性差，MoSi₂晶体中价电子结构的分布不均匀，晶体中强弱键交错是导致晶体脆性的主要原因。在应力作用下容易因弱键断开而产生微裂纹，故造成MoSi₂具有较高的本征脆性。

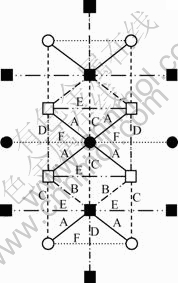
图2  MoSi₂晶胞各键在(100)面上的投影

Fig.2  Projection draws of every bonds in MoSi₂ cell on (100)

Plane: ○—Mo(on 0a); ●—Mo(on 0.5a); □—Si(on 0a) ;

■—Si(on 0.5a)

5  结论

1) MoSi₂晶体Mo原子处于丙种杂化第3阶，其中晶格电子为0.949 2，共价电子为4.949 2；而Si原子处于第1阶，晶格电子为2，共价电子为2。理论结合能为1 677.1 kJ/mol，与实验值吻合。

2) 由于Si原子偏移，沿c轴方向的分布的最近邻Si—Si原子键键距最短，共价电子数最多，n_D=  0.402 04。

3) MoSi₂晶体良好的导电性主要来自于Mo—Si成键时，Si的杂阶向较低的杂阶方向移动，大幅增加了MoSi₂晶体中的晶格电子数，使MoSi₂中晶格电子数比反应前Mo，Si原子的晶格电子数之和大。

4) MoSi₂晶体中价电子结构的分布不均匀，晶体中强弱键交错是导致晶体脆性的主要原因。

REFERENCES

[1] Sharif A A, Misra A, Petrovic J J, et al. Alloying of MoSi₂ for improved mechanical properties[J]. Intermetallics, 2001, 9(10/11): 869-873.

[2] Petrovic J J. Toughening strategies for MoSi₂-based high temperature structural silicides[J]. Intermetallics, 2000, 8(9/11): 1175-1182.

[3] Zachariasen W. The crystal structure of MoSi₂ and WSi₂[J]. Physik Chem, 1927, 128: 39-48.

[4] Harada Y, Morinaga M, Saso D, et al. Refinement in crystal structure of MoSi₂[J]. Intermetallics, 1998, 6(6): 523-527.

[5] Tanaka K, Nawata K, Inui H, et al. Refinement of crystallographic parameters in refractory metal disilicides[J]. Mater Res Soc, 2001, 646: 4.

[6] Bhattacharyya B K, Bylander D M, Leonard Kleinman. Comparison of fully relativistic energy bands and cohesive energies of MoSi₂ and WSi₂[J]. Phys Rev B, 1985, 32(12): 7973-7978.

[7] 周 飞. MoSi₂和WSi₂相结构和性能的电子理论研究[J]. 硅酸盐学报, 2000(5): 462-464.
ZHOU Fei. Study on the structure and properties for MoSi₂ and WSi₂ phases by electron theory[J]. Journal of the Chinese Ceramic Society, 2000(5): 462-464.

[8] 徐万东，张瑞林，余瑞璜. 过渡金属化合物晶体结合能计算[J]. 中国科学A, 1988, 18(3): 323-330.
XU Wang-dong, ZHANG Rui-lin, YU Rui-huang. Calculation cohesive energy of transition metal compounds[J]. Science in China A, 1988, 18(3): 323-330.

[9] 张瑞林. 固体与分子经验电子理论[M]. 吉林: 吉林科学技术出版社，1993.
ZHANG Rui-lin. Empirical Electron Theory of Solid and Molecules[M]. Jilin: Jilin Science and Technology Press, 1993.

[10] Mattheiss L F. Calculated structural properties of CrSi₂, MoSi₂, and WSi₂[J]. Physical Review B, 1992, 45(7): 3252-3259.

[11] Kittel C. Solid State Physics [M]. New York: John Wiley and Sons Inc, 1976.

[12] 陈舜麟，顾 强，王天民. Co₃Ti与CoTi的晶体结构与结合能的计算及其脆性[J]. 物理学报, 1995, 44(6): 936-942.
CHEN Shun-lin, GU Qiang, WANG Tian-ming. Constants of the intermetallic compounds Co₃Ti and CoTi and their brittleness [J]. Acta Physica Sinica, 1995, 44(6): 936-942.

[13] 贾 堤，董治中，于申军，等. TiMe合金的价电子结构分析及结合能计算[J]. 稀有金属材料与工程, 1998, 27(3): 152-155.
JIA Di, DONG Zhi-zhong, YU Shen-jun, et al. Calculation of cohesive energies and analysis of valence electronic structures of TiMe alloys[J]. Rare Metal Materials and Engineering, 1998, 27(3): 152-155.

[14] Takata M. The influence of the completeness of the data set on the charge density obtained with the maximum-entropy method.
A Re-examination of the Electron-Density Distribution in Si[J]. Acta Cryst A, 1996, 52: 287-290.

[15] 殷景华，郑 馥，李 雪，等. PtSi的价电子结构[J]. 材料研究学报, 2000, 6: 643-646.
YIN Jin-hua, ZHENG Fu, LI Xue, et al. PtSi valence electronic structures[J]. Chinese Journal of Materials Research, 2000, 6: 643-646.

[16] Shackelford J F, Alexander W. CRC Materials Science and Engineering Handbook [M]. Boca Raton: CRC Press LLC, 2001.

[17] 王沿东，孙祖庆，蔡 军，等. TiAl金属间化合物价电子结构即脆性[J]. 科学通报, 1991, 24: 1899-1902.
WANG Yan-dong, SUN Zu-qing, CAI Jun, et al. Valence electron structure of TiAl and its brittleness[J]. Chin Sci Bull, 1991, 24: 1899-1902.

[18] 杜晓东，丁厚福，宣天鹏. CrB价电子结构对其性能的影响[J]. 中国有色金属学报, 2005, 12: 1980-1985.
DU Xiao-dong, DING Hou-fu, XUAN Tian-peng. Effect of valence electron structure on property of CrB[J]. The Chinese Journal of Nonferrous Metals, 2005, 12: 1980-1985.

基金项目：国家自然科学基金资助项目(50472078); 教育部博士点基金资助项目(20040533006)

收稿日期：2006-07-25；修订日期：2006-11-29

通讯作者：易茂中，博士，教授；电话：0731-8830894；E-mail: yimaozhong@126.com

(编辑 何学锋)