DOI： 10.11817/j.issn.1672-7207.2019.09.014

基于泛在位置数据的城市道路网精细建模

邓敏¹,佘婷婷¹,黄金彩¹,刘慧敏¹,张建国²,郑旭东²

（1. 中南大学 地球科学与信息物理学院，湖南 长沙，410083；

2. 博通智慧城市研究院，湖南 长沙，410007）

摘要:为解决当前城市道路网自动提取方法难以同时对道路几何、拓扑、语义进行精细建模的问题，提出一种基于泛在位置数据的城市道路网一体化精细建模方法。首先，利用轨迹转向角热点分析方法提取道路交叉口区域，对交叉口和路段进行分治；然后，识别道路交叉口的出、入口点，分别采用低频轨迹聚类和交叉口连通性分析方法，识别交叉口的转向模式，并对路段轨迹进行分类，在此基础上对道路网几何、拓扑结构进行精细建模；最后，利用自然语言处理和地图匹配技术，利用位置文本数据和车辆轨迹数据提取道路名称和平均速度等信息，实现道路网几何、拓扑、语义精细建模。研究结果表明：本文方法能够用于快速获取城市道路网几何、拓扑、语义信息并精细建模。

关键词:道路网精细建模；泛在位置数据；道路语义信息；道路网几何拓扑结构

中图分类号:P208    文献标志码:A     文章编号:1672-7207（2019）09-2171-13

Fine road network modeling based on ubiquitous location data

DENG　Min¹, SHE　Tingting¹, HUANG　Jincai¹, LIU　Huimin¹, ZHANG　Jianguo², ZHENG　Xudong²

(1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China；

2. Botong Smart City Research Institute, Changsha 410007, China)

Abstract: To solve the problem that the automatic extraction method of road network is difficult to be elaborated in geometry, topology and semantics at the same time, a road network fine modeling method based on ubiquitous position data was proposed. Firstly, the road intersection area was extracted by the trajectory steering angle hot spot analysis method, and the intersection and the road section were divided. Secondly, the entrance and exit points of the road intersection were identified. The low-frequency trajectory clustering and intersection were respectively adopted to identify the steering mode of the intersection and classify the road segment trajectories, and further model the road network geometry and topology. Finally, the natural language processing and map matching techniques were used to obtain the position text data and the vehicle, trajectory data information such as road name and average speed was extrated to realize road network geometry, topology and semantic fine modeling. The results show that the proposed method can be used to effectively acquire and model the road network data with complete geometric topology and rich semantics.

Key words: road network fine modeling; ubiquitous location data; road semantics; road geometry and topology

道路网地理空间数据作为国家基础地理信息的重要组成部分，在智慧城市、智能交通以及居民日常生活方面发挥着重要的作用。随着城市交通的迅速发展，道路网结构日益复杂，几何拓扑精细、语义信息丰富、更新速度高的精细道路网信息成为智能交通和智慧城市建设中的关键需求。然而，传统的道路网数据采集方法需通过专业人员测绘或者卫星影像矢量化等，需要投入大量的人力和物力，成本较高^[1]。新兴的泛在位置数据如车辆轨迹数据、社交媒体签到数据、兴趣点POI数据等具有来源广泛、实时、语义信息丰富等优点，在道路网几何、拓扑、语义的精细建模方面具有巨大的潜力，因此，利用泛在位置数据进行道路网精细建模已成为当前研究的热点问题。目前，基于泛在位置数据的道路网提取算法主要包括栅格化方法^[2-4]、增量融合法^[5-7]以及聚类法^[8-10]。其中，栅格化方法的核心思想是将轨迹数据转化为灰度图像或者密度图像，采用数学形态学方法对图像进行膨胀和腐蚀操作来提取道路网；增量融合法主要以随机选取的1条轨迹作为初始路段，不断融入新轨迹线作为新增的路段，并提取整体道路网；聚类化法主要对轨迹点或轨迹线进行聚类并获得点簇或线簇，通过连接聚类中心点或线来提取道路网。这些方法主要用于提取道路网几何形态，且结构不够精细，尤其在交叉口处，几何拓扑结构信息丢失严重。此外，道路网语义信息(如道路名称、等级、速度信息)对于提供个性化导航服务、实现智能交通管控等方面具有重要作用。国内外相关学者利用泛在位置数据提取道路语义信息估计道路的平均行驶时间^[11-12]，对提取车道速度限制^[12]、拥堵^[13-15]和道路等级^[12,16]等进行了研究，这些信息的获取通常需要与已有道路网匹配。然而，道路网日新月异的变化导致匹配的效果和效率都很不理想，难以提取道路网语义信息。为此，本文作者提出一种利用泛在位置数据对城市道路网几何、拓扑、语义进行精细建模的方法。首先，提取道路交叉口的位置和范围信息，实现交叉口和路段的分治；然后，针对道路交叉口内轨迹和路段轨迹进行分类，实现道路网精细的几何拓扑结构建模；最后，利用签到POI等位置文本和轨迹速度信息，提取道路交叉口转向规则、道路名称、速度等语义信息。

1 道路交叉口和路段分治策略

1.1　交叉口的位置和范围提取

据统计，60%的轨迹都为低频采样轨迹^[17]。由于低频轨迹数据存在定位精度低、采样稀疏等问题，若根据角度方向阈值识别转向角变化较大轨迹点，则难以准确识别道路交叉口的位置和区域。然而，大量的轨迹点倾向于在交叉口处表现出较相似的时空、语义特性；轨迹点转向角亦具有较强空间相关性，表现为交叉口区域的高值正相关(热点)和路段区域的低值正相关(冷点)。采用局部空间自相关分析^[18]探测交叉口内轨迹转向角热点，并利用自适应空间点聚类方法^[19]进行热点聚类，识别交叉口的位置、范围。

令T={P₁, P₂, , P_N}为任一轨迹，其中，P_i为轨迹第i个采样点，

(1)

式中：i=1，2，…，N；x_i为轨迹点P_i的横坐标；y_i为轨迹点P_i的纵坐标； t_i为轨迹点P_i的当前采样时间；v_i为轨迹点P_i的瞬时速度；θ_i为轨迹点P_i的瞬时行驶方向角。利用热点分析识别道路交叉口位置和范围，如图1所示。图1(a)中，轨迹转向角定义为a_i = |θ_i -θ_i-1|。轨迹点转向角的局部空间G*统计值^[18]为

(2)

式中：N为空间邻域内轨迹点i的邻域轨迹点个数。w_ij为点p_i的空间权重。局部G*统计值是一种度量空间要素自相关程度的指标，用以测度空间要素与周围领域要素之间的相关程度，其中，正相关表示该要素与周围邻域要素的属性(如轨迹点转向角)呈正相关性，分为热点(高值正相关)和冷点(低值正相关)。某个轨迹点划分为热点的邻域内轨迹点的转向角都普遍较大，在空间上聚集于道路交叉口内，如图1(b)所示。局部G*统计能有效避免空间异常的影响，对轨迹点的噪音具有稳健性。本文将1%置信区间(G*>2.58)下的热点识别为交叉口轨迹点。

图1　利用热点分析识别道路交叉口位置和范围

Fig. 1　Identifying location and boundary of road intersections by hotspot analysis

轨迹转向角热点分析能有效区分交叉口区域轨迹点和非交叉口区域轨迹点。进而，利用自适应空间点聚类算法(即ASCDT算法^[19])进行热点空间聚类，以区分不同道路交叉口并提取交叉口的数量、位置和范围。ASCDT算法能够有效处理轨迹热点的不同形状、密度和等级所造成的空间异质性。通过分析ASCDT算法得到的结果，认为空间点簇的个数即为交叉口的个数，每个空间点簇的最小外接圆所覆盖的空间区域为道路交叉口的覆盖范围。

1.2　交叉口出入口检测

道路交叉口定义为连接3条及以上分支道路的区域^[20]，而每条分支道路都有1个入口和出口(单向通行道路只有1个入口或出口)。车辆轨迹由于受交叉口几何、拓扑结构的限制，会从分支道路的入口进入交叉口，并选择另一出口离开交叉口区域，因此，每条轨迹会在交叉口区域产生1个入口点和出口点，称为候选入口点和候选出口点。这些候选出入口点可通过计算轨迹和交叉口范围的交点得到。

设轨迹T的一段{P_i, P_i+1}与交叉口边界相交，并产生候选出入口点。由于低频轨迹具有低质量、低采样率等特性，{P_i, P_i+1}可能与多个交叉口相交，如图2所示。轨迹T_j的一段{P_s, P_s+1}与56号和57号交叉口相交。对于某一特定交叉口，轨迹段{P_i, P_i+1}与其空间相交关系仅包含以下3种：

1) {P_i, P_i+1}进入交叉口，产生1个候选入口点e_i，如轨迹T_i的一段{P_i, P_i+1}与47号交叉口相交，产生1个候选入口点e_i。

2) {P_i, P_i+1}离开交叉口，产生1个候选出口点e_j，如轨迹T_i的一段{P_j, P_j+1}与47号交叉口相交，产生1个候选出口点e_j。

3) {P_i, P_i+1}通过交叉口区域，同时产生候选入口点e_k和候选出口点e_t，如轨迹T_i的一段{P_k, P_k+1}与58号交叉口相交，产生候选入口点e_k和候选出口点e_t。

基于上述轨迹段{P_i, P_i+1}与道路交叉口空间相交关系的类型，对研究区域内轨迹进行空间分段，可得到研究区域内所有轨迹与交叉口的交点，即候选出入口点。提取候选出入口点的计算流程见算法1。

算法1 候选出入口点识别算法

图2　轨迹分段

Fig. 2　Track segmentation

图3　基于候选出入口点自适应聚类的交叉口的出入口检测

Fig. 3　Intersection entrance and exit detection by adaptive clustering of candidate entrance and exit points

其中：C_M为研究区域中提取得到的所有交叉口数据；C_m为与该轨迹相交的交叉口数据集；s为循环变量；C_s为C_m的子集。根据算法1，可在研究区域内识别所有候选入口点E_entr和出口点E_exit。记录这些候选点所属轨迹ID、所属交叉口ID、坐标(x，y)等信息，将这些候选点进行标准化记录为

(3)

式中：K为研究区域中共有K个候选出入口点；tt_id为点e_i所属的轨迹编号；c_id为点e_i所属的交叉口编号；(x, y)为点e_i的坐标；t_p用以表示点e_i为候选入口点(t_p=0)或者候选出口点(t_p=1)。根据候选出入口点所在轨迹的位置，可以将轨迹划分为交叉口内轨迹T_int(见图2中虚线)和路段轨迹T_out(见图2中实线)。

在提取候选出入口点E的基础上，选择任一交叉口内候选出入口点E_(cid=i)，利用ASCDT算法对E_(cid=i)进行聚类，如图3(b)所示。该交叉口候选出入口点被识别为5个簇，为该交叉口连接了5个分支道路。将识别的簇划分为候选入口点簇E_{(cid=i, tp=0)}和候选出口点簇E_{(cid=i, tp=1)}，分别计算候选入口点簇E_{(cid=i, tp=0)}和候选出口点簇E_{(cid=i, tp=1)}的平均坐标即为真实道路出入口位置，如图3(c)所示，其中，红色方框为交叉口入口点检测结果，黑色圆框为交叉口出口点检测结果。

2 道路网几何拓扑精细建模

2.1　交叉口转向模式聚类

2.1.1　轨迹几何相似性度量

为了对交叉口进行精细几何、拓扑建模，需要识别交叉口内转向模式。记T₁={P₁, P₂, , P_m}，T₂={P₁, P₂, , P_n}为2条交叉口内轨迹，由于轨迹采样的稀疏性，T₁和T₂轨迹点之间并非存在一一对应关系，从而需要对轨迹进行重新采样。通常在2个采样点之间以dl(通常设置为25 m)为步长，等步长插入轨迹点。然后，以r为阈值(通常设置为25 m)，定义2条轨迹之间的公共子轨迹。一般地，轨迹上可能存在多段公共子轨迹，记第i段公共子轨迹为s_i，最长公共子轨迹为，计算式为

(4)

同理可计算T₂的最长公共子轨迹。于是，T₁与T₂之间的最长公共子轨迹的相似性定义为

(5)

其中：|T₁|表示轨迹T₁的整体长度。

2.1.2　轨迹方向相似性度量

考虑到道路含2个不同行驶方向，识别交叉口转向模式需要顾及轨迹方向信息。车辆轨迹的方向相似性定义为2条轨迹之间方向的差异。为量化这种差异，对轨迹T₁建立一种“距离-方向”函数F₁(x)，定义为

if x_i≤xi₊₁, 0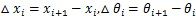

式中：x∈[0, 1]，是方向函数F₁(x)的独立变量；x_i∈[0, 1]，是从轨迹起点到轨迹上任一点P_i的累积长度与轨迹整体长度的比例，即轨迹段{P₁, , P_i}与轨迹整体{P₁, , P_m}的长度之比；△x_i为相邻轨迹点P_i+1和P_i累计长度比例差异；△h_i为相邻轨迹点P_i+1和P_i的行驶方向角。由式(6)可知，“距离-方向”函数是分段线性函数，如图4所示。

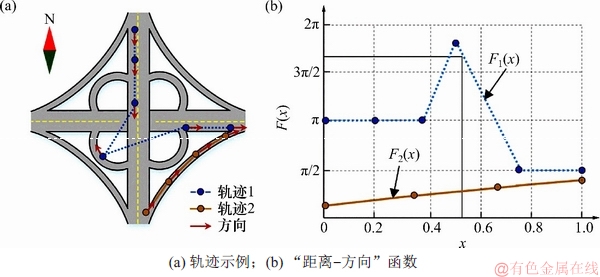
图4　轨迹的“距离-方向”函数

Fig. 4　“Distance-direction” function of trajectories

给定变量x∈[0, 1]，轨迹T₁和T₂的“距离-方向”函数分别描述为F₁(x)和F₂(x)，进而轨迹T₁和T₂的方向相似性计算式为

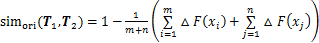(7)

式中：x_i和x_j分别为轨迹点P_i∈T₁ 和P_j∈T₂的累积长度比率；m和n分别为T₁和T₂的轨迹点个数；△F(x)为F₁(x)和F₂(x)的归一化差值，

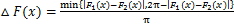(8)

基于轨迹的几何相似性和方向相似性，轨迹之间的总体相似性则可定义为sim(T₁, T₂)=sim_lcst(T₁, T₂)× 0.5+sim_ori(T₁, T₂)×0.5。则轨迹之间的距离矩阵可以定义为D=(d_ij)_N×N(其中，d_ij=1-sim(T_i, T_j))。

2.1.3　交叉口转向模式聚类　

由于同种转向模式轨迹之间存在较大相似性，因而，可利用轨迹层次聚类^[21]的方法，对交叉口内轨迹T_int进行聚类，用于探测交叉口内的转向模式。在层次聚类过程中，利用“凝聚法”自底向上进行聚类，直到所有轨迹合并为1个簇为止。同时，利用Davies-Bouldin指标^[22]对聚类结果有效性进行评价(即DB指标)，识别合理的转向模式个数。本文将聚类个数设置为n₁~n₂(实验中设置为2~40)，选择DB指数最小时对应的聚类个数K为最佳聚类结果。通过分析DB指标可以发现，有效的聚类簇内部应足够紧密，且簇与簇之间具有较大分离性，可通过计算簇的紧密性和分离性比率对聚类结果进行评价。因此，DB指标越小，聚类有效性越强。

2.2　路段轨迹分类

在出入口识别的基础上，轨迹被划分为交叉口内轨迹T_int和路段轨迹T_out，其中，可从T_out中提取路段的几何、拓扑结构信息。通过分析交叉口连通性对路段进行几何、拓扑精细建模。

T_out可划分为2类：包含1个候选出入口点的轨迹和包含多个候选出入口点的轨迹。交叉口及其拓扑连接矩阵示意图如图5所示(其中，0表示无连接，1表示存在连接)。由图5可知包含1个侯选出入口的轨迹所在的路段为悬挂路段，由于候选出入口点信息包含所属交叉口编号，因此，构造交叉口之间的拓扑连接矩阵D，根据交叉口的拓扑连通性对路段轨迹进行分类。如图5所示，矩阵内元素D(i×j)为交叉口之间的同一类连接模式，即交叉口i与j之间有轨迹连接。由于存在单向通行道路的存在，因此，矩阵D是非对称矩阵，若存在交叉口3到5的轨迹，而5到3的轨迹不存在，则所提方法具有提取车道级道路网的能力。

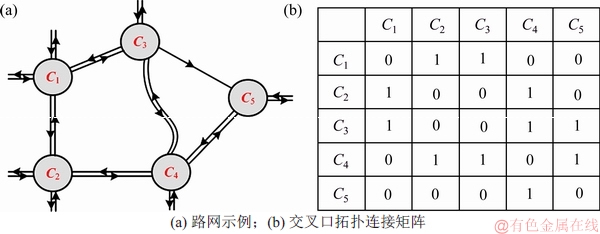
图5　交叉口及其拓扑连接矩阵示意图

Fig. 5　Intersections and topological connection matrix

根据交叉口之间的拓扑连接矩阵D(N×N)，可对轨迹进行分类。首先，根据D(N×N)筛选出属于同种连接模式D(i×j)的路段轨迹T_out(i, j)；然后，利用2.1.3节所提轨迹聚类方法对T_out(i, j)进行聚类。由于受道路交叉口探测精度影响，若干道路交叉口未被探测，本文对T_out(i, j)进行聚类可识别不同连接路径，从而考虑交叉口探测精度的影响。2条交叉口之间轨迹T_out(i,j)的不同连接模式如图6所示，其中，实线为交叉口的不同连接路径，本文方法能够对其有效识别。

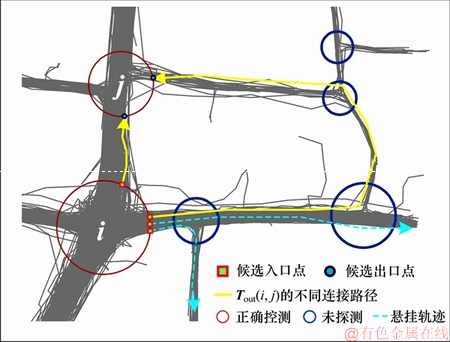
图6　2个交叉口之间轨迹T_out(i,j)的不同连接模式

Fig. 6　Different connection modes of track T_out(i,j) between intersection i and j

对于悬挂路段(图6中虚线)，其特点在于只含1个候选出入口点，因此，分别提取每个交叉口的悬挂轨迹数据T_out(i)，根据2.1.3节轨迹聚类方法对T_out(i)进行聚类。在上述基于交叉口连通性分析和悬挂轨迹分类的基础上，可对研究区域路段轨迹T_out进行有效分类，进而对每一类轨迹的中心线进行提取，获得城市道路网的精细几何和拓扑结构。

2.3　道路网几何、拓扑结构精细建模

在对T_int和T_out进行聚类、分类的基础上，令C_L(i)为T_int或T_out的轨迹簇，采用K段主曲线算法^[23]提取C_L(i)的中心线即车道线，进而生成道路网，记为R_D。

K段主曲线由VERBEEK等提出^[24]，采用局部主成分分析的方法来计算第K条线段，依据光滑性连接形成主曲线，如图7所示。K段主曲线的算法步骤主要由以下几步组成。

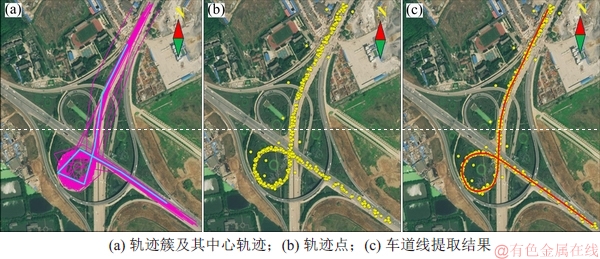
图7　利用K段主曲线提取车道线

Fig. 7　Extracting lane lines using K-segment principal curve

Step 1：初始化。输入轨迹点数据P=(P₁, P₂, , P_n)，计算第1主成分，并取3σ为初始的线段长度，其中σ是第1主成分的标准差，得到初始线段l₁和其Voronoi区域V₁。

Step 2：插入新线段。若k≤k_max，则计算P_i并满足：

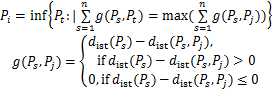(9)

式中：d_ist(P_s)=min d(P_s,l_j)，为P_s与线段l_j之间的最小距离；d_ist(P_s,P_j)=||P_s-P_j||²，为P_s与P_j之间距离的平方；j∈1~k。计算点P_i的Voronoi区域V_q并取V_q的第1主成分线，以3σ作为新增线段l_k的长度并记录其Voronoi区域V_k。

Step 3：调整。若新增线段后，所有线段旧的Voronoi区域{V₁，V₂，…，V_k}与新的Voronoi区域{V_1′, V_2′，…，V_k′}不同，则将新的Voronoi区域赋给旧的Voronoi区域，并重复Step 2，直到Voronoi区域不变为止。

Step 4：优化。将k条线段构造成哈密顿回路，并利用城市旅行商问题(TSP)进行优化形成哈密顿回路。

3 基于车辆轨迹和签到文本的道路网语义信息建模

3.1　交叉口转向规则语义提取

交叉口内轨迹簇的转向规则可通过挖掘每条轨迹的转向规则得到。交叉口转向规则判别如图8所示。

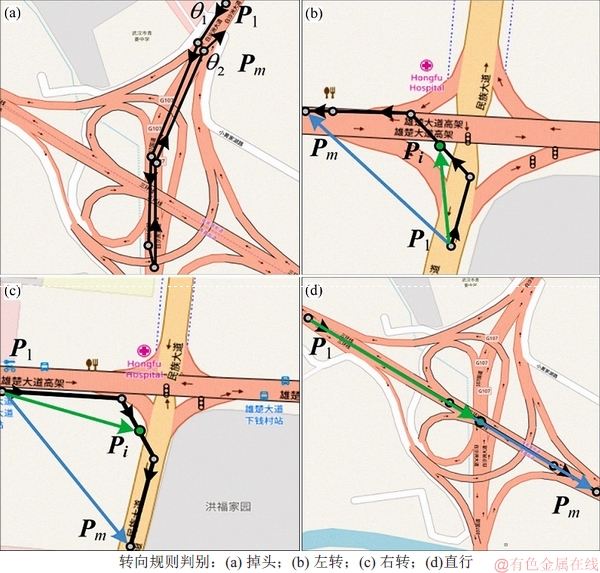
图8　交叉口转向规则判别

Fig. 8　Intersection turning rules inference

设P₁为轨迹起始点，P_m为该轨迹终点，θ₁和θ₂分别为P₁和P_m的行驶方向角，P_i为轨迹上任一点，则该轨迹的转向规则如下：

1) 若θ₁-θ₂ ≈ ±180^°，则转向规则为“掉头”；

2) 若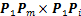(1＜i＜m)为正，则转向规则为“右转”；

3) 若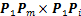(1＜i＜m)为负，则转向规则为“左转”；

4) 若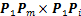(1＜i＜m)为零向量，则转向规则为“直行”。

通过上述分析可得到轨迹簇内每条轨迹的转向规则：当簇内超过50%以上轨迹判定为某一特定转向规则时，则该转向规则定义为轨迹簇的转向规则；当交叉口内未发现某个转向规则的轨迹簇时，则认为该转向规则在交叉口内是禁止的。

3.2　道路名称提取

地图POI和微博签到文本中包含大量与道路相关的信息，如道路名称等。本文利用高德地图POI和新浪微博签到文本数据，基于Jiaba分词技术(https://github.com/fxsjy/jiebademo)，从这些位置文本的地址字段中将道路名称划分出来。如对于POI地址“湖北省武汉市江汉路527号，武汉美术馆对面”，利用Jieba中文分词之后的结果为：“湖北省/武汉市/江汉路/527/号/，/武汉/美术馆/对面”。进而，提取出含有“路”“大道”“ 街道”和“街”关键词的词语。

由于POI数量众多，密度空间分布差异大，可将POI与道路网进行匹配，以50 m为缓冲区，提取道路路段的缓冲区内的POI数据，如图9所示。然后，基于Jieba分词技术提取其缓冲区内POI所含道路名称，生成道路名称频度直方图，并选取频度最大的道路名称为该路段道路名称。从图9可见：示例路段的名称可以描述为“丁字桥路”。

3.3　道路网平均速度提取

将所提取道路网按100 m进行重采样(即速度信息识别的空间分辨率设置为100 m)，记为R_D={e₁, e₂, , e_m}，并将GPS轨迹点与所建模的道路网进行匹配。于是，道路网R_D的每条边e_i都有若干GPS点(记为P_ei={P₁, P₂, , P_ni})与之匹配，这些GPS点的时间和速度信息可用于提取道路网的速度信息。将P_ei划分为24个时段，统计路段e_i在24个时段内平均速度信息，从而获得整个路网R_D在24个时段内的速度信息。

4 实验结果与分析

4.1　实验数据

为验证本文方法的有效性，选取武汉市武昌区一块靠近长江南岸、面积约13 km×11 km的区域作为实验区域。该研究区域为武汉市人口、经济、商业较集中的区域，包含武昌火车站等交通枢纽和洪山广场等商业中心，并包含复杂道路网结构。如研究区域内包含了十字路口、T型路口、Y型路口、立交桥、环形路口等各种形态各异、结构复杂的道路交叉口。此外，在武昌火车站附近，道路网密度高，交叉口密集，适合验证本文所提方法在处理复杂路网、密集路网的有效性。选取2014年5月1日的浮动车GPS轨迹数据，包含1 129 466个轨迹点，经重采样和预处理后，含60 045条轨迹线。

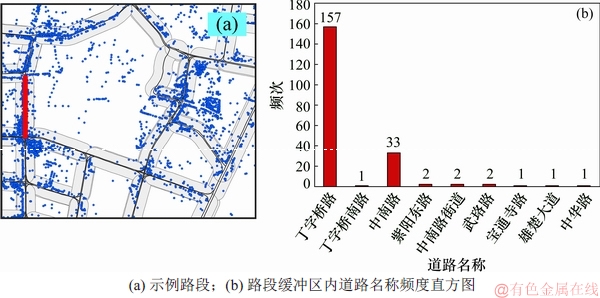
图9　利用缓冲区内POI进行道路段名称提取

Fig. 9　Road name extraction using POI in buffer for

4.2　道路交叉口位置和范围探测

利用热点分析和聚类方法对交叉口的位置和范围进行探测，结果如图10所示。

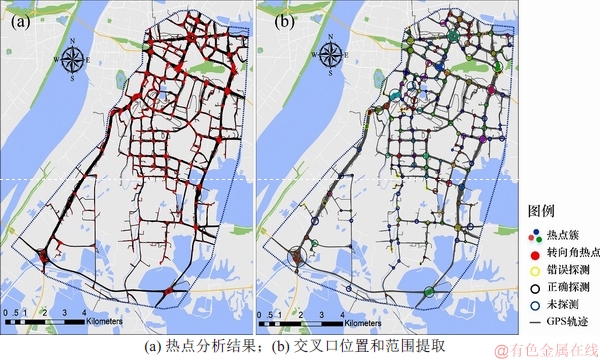
图10　研究区域交叉口探测结果

Fig. 10　Results of intersection detection of study area

从图10可见：转向角热点主要分布于交叉口区域，表明热点分析的有效性；此外，研究区域包含大量复杂类型的道路交叉口，空间分布密度不一、形态各异、大小和范围差异巨大，采用本文方法较好地探测了道路交叉口的位置和范围。为了对道路交叉口探测结果进行定量评价，采用本文方法与文献[24]中方法分别计算交叉口探测结果的精度P、召回率R和F，表达式为：

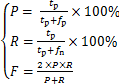(10)

式中：t_p为正确探测交叉口数量；f_p为错误探测交叉口数量；f_n为未探测交叉口数量。通过与百度地图、高德地图进行人工判别，经统计发现本文所提方法共识别道路交叉口157个，正确识别136个，错误识别21个，未识别26个。由式(10)可知：本文方法交叉口探测精度P、召回率R和F分别为86.6%，84.0%和85.3%；文献[24]所提方法共识别道路交叉口186个，正确识别138个，错误识别48个，未识别24个，因而，交叉口探测精度P、召回率R和F分别为74.2%，85.2%和79.3%。图11所示为本文方法和文献中[24]中方法所提路网与遥感影像的叠加对比结果。从图11可以发现：本文方法提取的道路骨架与影像中道路更加吻合，包含更少误提取的悬挂路段；同时，本文方法计算的交叉口探测精度P以及F明显比文献[24]中方法的效果好。从图11(b)可以发现本文方法可以有效地提取精细的复杂道路交叉口。

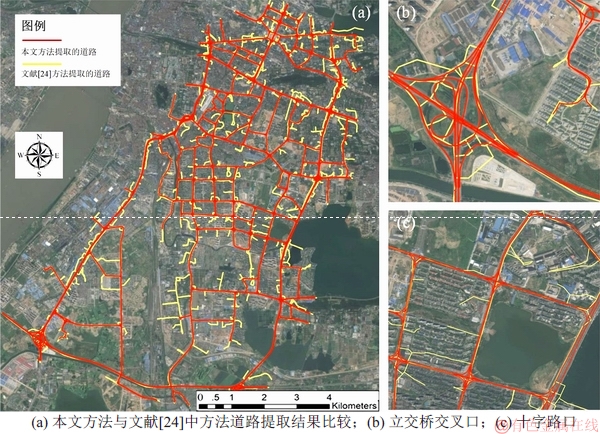
图11　本文方法与文献[24]中方法提取路网与遥感影像比较

Fig. 11　Comparison between remote sensing image and road network extracted by methods in the paper and Ref. [24]

4.3　道路网几何拓扑、语义精细建模结果

道路网精细几何拓扑结构、道路名称信息和速度信息的建模结果如图12所示。

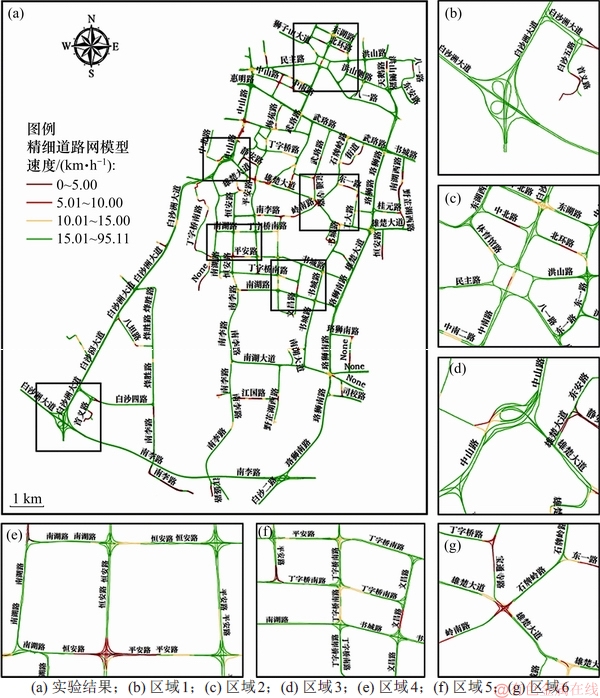
图12　道路网精细建模结果

Fig. 12　Fine road network modeling results

从图12可见：所生成的道路网具有名称、方向、速度等信息，在路段上包含2条车道线，也体现了本文方法在道路网精细建模方面的优势。其中，图12(b)所示为立交桥区域模拟结果，由于高程差异导致立交桥几何结构复杂，本文成功地对其进行了精细建模；图12(b)和(c)所示为较复杂道路交叉口模拟结果，其中，图12(b)左上角所示为包含高架式立交桥模拟结果，图12(c)所示为环形路口模拟结果。图12(d)~(f)所示分别为十字路口、“T”型路口、“Y”型路口较常见道路交叉口。可见，研究区域包含的道路交叉口形态各异、结构复杂，所提方法对研究区域道路网实现了精细建模，在路段和交叉口几何拓扑结构上，具有精细车道线；在语义信息方面，提取了道路网名称、速度等信息。

为了验证本文方法道路名称提取结果的有效性，通过对高德地图、百度地图进行人工判断，共识别含名称的道路237个，其中正确识别的道路名称为229个，错误识别的道路名称为8个，未识别的道路名称有8个，因而，道路名称识别的精度P、召回率R和F分别为97.0%，96.6%和96.8%，表明本文方法在复杂城市场景下道路网几何、拓扑、语义精细建模方面的有效性。

将所建模道路网的平均速度信息划分为24个时段，统计道路网24个时段内的平均速度，并划分到[0，5)，[5，10)，[10，15)和[15，+∞)共4个区间内，分析其时空特征。图13所示为其中4个主要时刻道路网平均速度的空间分布情况。从图13可见：道路网平均速度的空间分布在一定程度上表征了道路拥堵的时空分布特征。

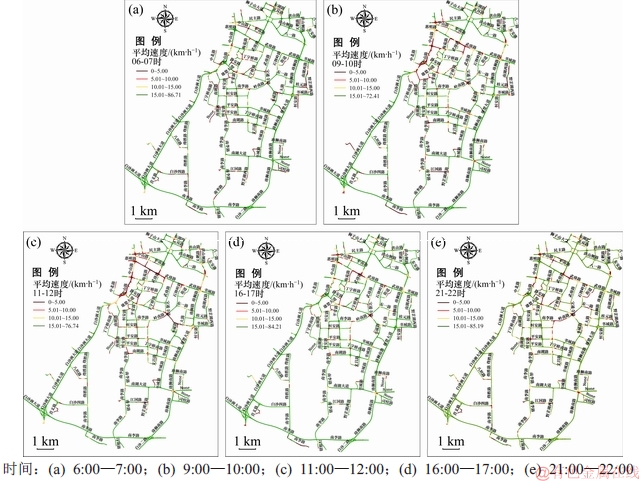
图13　道路网若干典型时段内平均速度信息

Fig. 13　Road network average speed information of several typical time

本实验中采用2014年5月1日的车辆GPS轨迹数据对道路网平均速度进行演化分析，可以发现：1) 9:00—12:00，武昌火车站附近具有明显的拥堵现象，这可能由于“五一节”旅游人数增多，导致上午在武昌火车站附近呈现明显的车流高峰，并且一直持续到12:00；2) 在24个时段内，研究区域下方的立交桥附近较少出现车辆行驶缓慢的现象，表明该区域无拥堵出现；3) 武珞路作为武汉市较繁华的路段，从8:00—16:00都具有明显的车辆行驶缓慢现象，而16:00后车行缓慢现象减轻；4) 雄楚大道与岭南路交叉口处，在9:00—12:00易发生拥堵，交通缓慢，此外，在20:00—23:00容易发生拥堵，表明该交叉口具有重要的交通地位。整体上看，10:00—12:00的拥堵情况最严重，这种拥堵现象可能与“五一节”假期出行高峰有关，16:00—22:00则易出现局部车行缓慢现象。

5 结论

1) 道路网精细几何、拓扑、语义信息是实现智能交通、导航及行车规划的前提。泛在位置数据由于具有动态、实时的特性，为道路网精细信息的实时获取提供了新的数据源。

2) 本文提出一种城市道路网几何、拓扑、语义信息一体化精细建模方法。利用武汉市车辆轨迹数据进行实验分析，验证了本文方法的有效性。所提方法可以满足快速实时道路网几何、拓扑、语义信息精细获取需要，为智慧城市建设、智能交通系统提供支持。

参考文献：

[1] 傅仲良, 吴建华. 多比例尺空间数据库更新技术研究[J]. 武汉大学学报(信息科学版), 2007, 32(12): 1115-1118.

FU Zhongliang, WU Jianhua. Update technologies for multi-scale spatial database[J]. Geomatics and Information Science of Wuhan University, 2007, 32(12): 1115-1118.

[2] CHEN Chen, CHENG Yinhang. Roads digital map generation with multi-track GPS data[C]//2008 International Workshop on Education Technology and Training & 2008 International Workshop on Geoscience and Remote Sensing. New York, USA: IEEE, 2008: 508-511.

[3] DAVIES J J, BERESFORD A R, HOPPER A. Scalable, distributed, real-time map generation[J]. IEEE Pervasive Computing, 2006, 5(4): 47-54.

[4] 蒋益娟, 李响, 李小杰, 等. 利用车辆轨迹数据提取道路网络的几何特征与精度分析[J]. 地球信息科学学报, 2012, 14(2): 165-170.

JIANG Yijuan, LI Xiang, LI Xiaojie, et al. Geometrical characteristics extraction and accuracy analysis of road network based on vehicle trajectory data[J]. Journal of Geo-Information Science, 2012, 14(2): 165-170.

[5] 唐炉亮, 刘章, 杨雪, 等. 符合认知规律的时空轨迹融合与路网生成方法[J]. 测绘学报, 2015, 44(11): 1271-1276.TANG Luliang, LIU Zhang, YANG Xue, et al. A method of spatio-temporal trajectory fusion and road network generation based on cognitive law[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(11): 1271-1276.

[6] WANG Jing, RUI Xiaoping, SONG Xianfeng, et al. A novel approach for generating routable road maps from vehicle GPS traces[J]. International Journal of Geographical Information Science, 2015, 29(1): 69-91.

[7] BIAGIONI J, ERIKSSON J. Map inference in the face of noise and disparity[C]//Proceedings of the 20th International Conference on Advances in Geographic Information Systems: SIGSPATIAL '12. Redondo Beach, California. New York: ACM Press, 2012: 79-88.

[8] ZHANG Lijuan, THIEMANN F, SESTER M. Integration of GPS traces with road map[C]//Proceedings of the Second International Workshop on Computational Transportation Science: IWCTS '10. San Jose, California, New York: ACM Press, 2010: 17-22.

[9] KARAGIORGOU S, PFOSER D. On vehicle tracking data-based road network generation[C]//Proceedings of the 20th International Conference on Advances in Geographic Information Systems: SIGSPATIAL '12.Redondo Beach, California, New York: ACM Press, 2012: 89-98.

[10] EDELKAMP S, SCHRDL S. Route planning and map inference with global positioning traces[M]. Heidelberg, Berlin: Springer, 2003: 128-151.

[11] 唐炉亮, 阚子涵, 黄方贞, 等. 利用低频时空GPS轨迹进行交叉口通行时间探测[J]. 武汉大学学报(信息科学版), 2016, 41(1): 136-142.

TANG Luliang, KAN Zihan, HUANG Fangzhen, et al. Travel time detection at intersections from taxis' trace data[J]. Geomatics and Information Science of Wuhan University, 2016, 41(1): 136-142.

[12] WINDEN K V, BILJECKI F, SPEK S V D. Automatic update of road attributes by mining GPS tracks[J]. Transactions in GIS, 2016, 20(5): 664-683.

[13] 郭雪婷, 秦艳丽, 雷震. 基于出租车GPS数据的城市道路拥堵判别[J]. 交通信息与安全, 2013, 31(5): 140-144.

GUO Xueting, QIN Yanli, LEI Zhen. Urban road congestion discrimination based on taxi GPS data[J]. Journal of Transport Information and Safety, 2013, 31(5): 140-144.

[14] 张志平, 汪向杰, 林航飞. 基于浮动车数据的高速公路拥堵检测方法[J]. 交通信息与安全, 2012, 30(6): 95-99.

ZHANG Zhiping, WANG Xiangjie, LIN Hangfei. A detection method of expressway traffic congestion with probe car data[J]. Journal of Transport Information and Safety, 2012, 30(6): 95-99.

[15] WANG Yuqi, CAO Jiannong, LI Wengen, et al. Exploring traffic congestion correlation from multiple data sources[J]. Pervasive and Mobile Computing, 2017, 41: 470-483.

[16] VAN WINDEN K, BILJECKI F, VAN DER SPEK S. Automatic update of road attributes by mining GPS tracks[J]. Transactions in GIS, 2016, 20(5): 664-683.

[17] ZHENG Kai, ZHENG Yu, XIE Xing, et al. Reducing uncertainty of low-sampling-rate trajectories[C]//Proceedings of the 28th International Conference on Data Engineering. Washington: IEEE, 2012: 1144-1155.

[18] ORD J K, GETIS A. Local spatial autocorrelation statistics: distributional issues and an application[J]. Geographical Analysis, 2010, 27(4): 286-306.

[19] DENG Min, LIU Qiliang, CHENG Tao, et al. An adaptive spatial clustering algorithm based on delaunay triangulation[J]. Computers, Environment and Urban Systems, 2011, 35(4): 320-332.

[20] WANG Jing, WANG Chaoliang, SONG Xianfeng, et al. Automatic intersection and traffic rule detection by mining motor-vehicle GPS trajectories[J]. Computers, Environment and Urban Systems, 2017, 64: 19-29.

[21] MULLNER D. Modern hierarchical, agglomerative clustering algorithms[J]. IEEE Transactions on Analysis and Machine Intelligence, 1979, PAMI-1(2): 224-227.

[22] DAVIES D L, BOULDIN D W. A cluster separation measure[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1979(2): 224-227.

[23] VERBEEK J J, VLASSIS N, KRSE B. A k-segments algorithm for finding principal curves[J]. Pattern Recognition Letters, 2002, 23(8): 1009-1017.

[24] AHMED M, WENK C. Constructing street networks from GPS trajectories[C]//Algorithms-ESA 2012. Berlin, Heidelberg: Springer, 2012: 60-71.

（编辑 陈灿华）

收稿日期： 2018 -11 -19; 修回日期： 2019 -03 -02

基金项目(Foundation item)：博通智慧城市研究院合作研发项目(BTZH2018002); 国家自然科学基金资助项目(41771452); 国家重点研发计划项目(2017YFB0503500)；中南大学研究生科研创新项目(2018zzts708)(Project(BTZH2018002) supported by the Cooperative Research and Development Program of Botong Smart City Research Institute; Project(41771452) supported by the National Natural Science Foundation of China; Project(2017YFB0503500) supported by the National Key Research and Development Program of China; Project(2018zzts708) supported by the Graduate Research Innovation Program of Central South University)

通信作者：黄金彩，博士，从事时空数据挖掘研究；E-mail: huangjincaicsu@163.com