Mg-5.3Zn-0.8Zr镁合金高温变形行为的热模拟研究
王 斌，易丹青，顾 威，方西亚，刘会群，吴春萍，王宏伟
(中南大学 材料科学与工程学院，湖南 长沙，410083)
摘 要：采用Gleeble-1500热模拟试验机进行压缩实验，研究Mg-5.3Zn-0.8Zr镁合金在变形温度为473~723 K、应变速率为0.01~1.00 s-1的变形行为。分析合金流变应力与应变速率、变形温度之间的关系，计算高温(573~723 K)下合金变形时的应力指数和变形激活能，并采用Zener-Hollomon参数法构建该合金高温塑性变形的本构关系。研究结果表明：在实验变形条件范围内，合金的真应力-真应变曲线为动态再结晶型；在573~723 K，应力指数随着变形温度升高而增加，而且增加的幅度逐渐增大，变形激活能随着变形温度和应变速率的改变而发生变化。
关键词：塑性变形；热模拟；动态再结晶；镁合金
中图分类号：TG 146.4 文献标识码：A 文章编号：1672-7207(2009)01-0123-06
Thermal simulation of hot deformation behavior for
Mg-5.3Zn-0.8Zr magnesium alloy
WANG Bin, YI Dan-qing, GU Wei, FANG Xi-ya, LIU Hui-qun, WU Chun-ping, WANG Hong-wei
(School of Materials Science and Engineering, Central South University, Changsha 410083, China)
Abstract: The hot deformation behavior of a Mg-5.3Zn-0.8Zr magnesium alloy was investigated by hot compressive tests on Gleeble-1500 thermal simulation test machine at 473-723 K and at the strain rates of 0.01-1.00 s-1. The relationships of flow stress, strain rate and deformation temperature were analyzed, the stress exponent and the deformation activation energy at elevated temperatures (573-723 K) were calculated. The constitutive equation of the plastic deformation of Mg-5.3Zn-0.8Zr alloy at elevated temperatures (573-723 K) was obtained by introducing Zener-Hollomon parameter. The results show that the true stress-strain curves of the alloy have dynamic recrystallization character under the present deformation conditions; within the range from 573 K to 723 K temperature, the stress exponent increases with the increase of deformation temperature and the increment increases gradually. The deformation activation energy changes with the deformation temperature and strain rate.
Key words: plastic deformation; thermal simulation; dynamic recrystallization; magnesium alloy
镁合金是目前工业上可应用的密度最低的金属结构材料[1]，其密度仅为铝的2/3，钢的1/4，镁合金还具有高的比强度和比刚度以及优良的减震性、导热性、电磁屏蔽性、易切削性和易回收性，被誉为“21世纪的绿色工程金属材料”[2]。但由于镁合金晶体结构的特殊性导致其难于在室温下进行塑性变形，这使得镁合金，特别是变形镁合金的发展受到极大的限制。镁及其合金层错能较低[3]，其滑移面上的扩展位错较宽，难于从节点和位错网中解脱出来，也难于通过交滑移和攀移而与异号位错相互抵消，动态回复过程进行得很慢，亚组织中位错密度较高，剩余的储能足以引起再结晶[4]，因此动态再结晶可能成为改善镁合金塑性及细化组织的途径之一。有必要探讨热加工工艺参数对镁合金组织变化的影响，特别是对动态再结晶行为的作用进行研究。Mg-5.3Zn-0.8Zr合金是一种优良的变形镁合金[5]，由于其具有较高的强度、良好的工艺塑性及可热处理强化等优点使其成为高强韧镁合金的研究热点之一。Mukai等[6-8]对该合金的研究主要侧重于合金的超塑性变形能力，对合金在不同变形条件下，特别在较高应变速率条件下变形行为的研究很少。余琨等[9]对Mg-5.6Zn-0.7Zr-0.8Nd合金高温塑性变形进行了热模拟研究，发现在热变形过程中不同温度下流变应力呈现不同形式，合金变形激活能随应变速率增加而增加；郭强[10]等对AZ31镁合金高温压缩性能进行了研究，发现材料流变应力和纤维组织强烈地受到变形温度的影响。当变形温度低于350 ℃时，流变应力呈现幂指数关系；高于350 ℃时，流变应力呈现指数关系。刘志义等[11]对ZK31+0.3Yb镁合金的流变应力和组织演变进行研究，认为温度为663 K、应变速率为0.1 s-1是该合金最佳的变形条件，但以上研究都未涉及Mg-5.6Zn-0.7Zr合金，对该合金在高温下变形行为未开展研究。Galiyev等[12]对比纯镁和ZK60 (Mg-6.0Zn-0.7Zr)镁合金的塑性变形机理时发现，ZK60镁合金在高温区(473~523 K)随着温度的升高，应变硬化和软化效应明显减弱，并计算了ZK60镁合金在573 K下的硬化指数，但未对该合金的变形激活能Q在不同温度和不同应变速率下的变化规律进行讨论。在此，本文作者研究Mg-5.3Zn-0.8Zr合金在不同变形速率下的高温变形行为，变形过程中的应力应变指数n、变形激活能Q等参数与温度等变形参数的关系，以期为制定合理的热加工工艺提供指导，同时也为开展高强韧镁合金加工过程的数值模拟研究提供必要的实验依据。
1 实 验
实验用镁合金名义成分为Mg-5.3Zn-0.8Zr(质量分数，%)。采用电阻炉熔炼，熔剂保护，金属模浇注成型。铸锭经均匀化处理后，机加工成直径×高为 10 mm×15 mm的圆柱形压缩试样。热压缩实验在Gleeble-1500热模拟机上进行。变形温度为473~723 K，应变速率为0.01，0.10、0.50和1.00 s-1，预设最大变形程度为60%。压缩前升温速度为2 ℃/s，保温 5 min，变形结束后立即水淬。为减小压缩时试样两端面的摩擦力，在压缩试样两端开浅凹槽，以便加入含石墨的固体润滑剂。
2 结果与分析
2.1 合金的真应力-真应变曲线
图1所示为ZK60镁合金在不同应变速率下等温压缩时的真应力-真应变曲线。从图1可看出，在所有变形温度和应变速率条件下，流变应力均是先随着应变增加而增加，达到峰值后，开始下降，并逐渐趋于稳定。由文献[13-14]可知，合金的真应力-真应变曲线属于动态再结晶型。
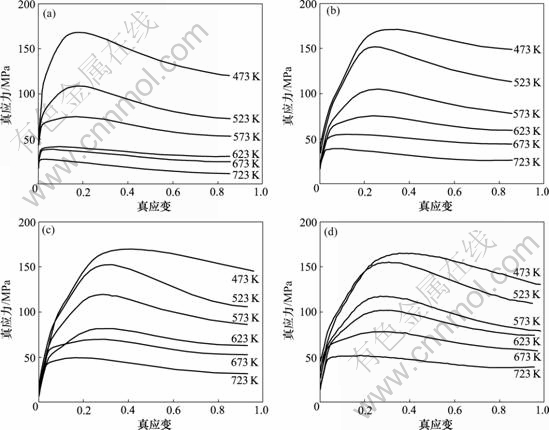
应变速率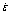
/s-1: (a) 0.01; (b) 0.1; (c) 0.5; (d) 1
图1 Mg-5.3Zn-0.8Zr合金在不同应变速率下的真应力-真应变曲线
Fig.1 True stress-strain behaviors of Mg-5.3Zn-0.8Zr magnesium alloy with various strain rate at different temperatures
从图1还可看出，随着变形温度降低或应变速率增大，峰值流变应力和峰值应力所对应的应变均增加，这表明变形温度的降低和应变速率的增大将不利于发生动态再结晶。在相同的温度(573～723K)下，流变应力随着应变速率增加而增大，并且峰值应力所对应的应变量也随着应变速率的增加而增加，这可能是随着应变速率增大，单位应变的变形时间缩短，可动位错的数目增加，导致再结晶的驱动力和加工硬化作用都增大；而动态回复和动态再结晶的软化过程却缩短，总的结果是加工硬化速率超过了动态再结晶的软化速率。因此，动态再结晶软化与加工硬化两者作用，相互平衡时的峰值应力及其所对应的应变均增大。实验结果表明，这种规律在温度为473 K和523 K时并不明显，而在573~723 K表现明显，并且随着温度的升高而更加显著。这表明与中温(473~573 K)变形相比，合金在高温(573~723 K)变形时对应变速率更为敏感。
图2所示为ZK60镁合金在温度为623 K、应变速率为0.1 s-1条件下变形后组织随应变量演变的金相组织形貌。在变形初始(应变量ε=0.12)，晶界出现弯曲，可观察到少量晶界弓弯的存在，金相上观察不到有动态再结晶发生。在该应变量条件下，对应的真应力-真应变曲线呈上升趋势，但斜率较小，此时应力软化主要由动态回复引起。当应变量增加到接近峰值应变时(应变量ε=0.24)，原始晶粒经过变形已被拉长，能观察到在某些晶界处形成的再结晶小晶粒，表明动态再结晶已开始发生。当应变量比较大时(应变量ε=0.60)，原始晶粒被形成于晶界附近的大量的动态再结晶晶粒所包围。此时对应的真应力-真应变曲线呈下降趋势，表明由于动态再结晶所引起的应力软化作用已高于加工硬化效果。进一步增大应变量(应变量ε=0.93)，剩余的原始晶粒组织已经比较少，动态再结晶晶粒区变宽，并且剩余的原始晶粒的形状近似于扁的菱形。此时对应的真应力-真应变曲线的下降趋势已很弱，表明动态再结晶引起的应力软化与加工硬化即将趋于新的平衡。
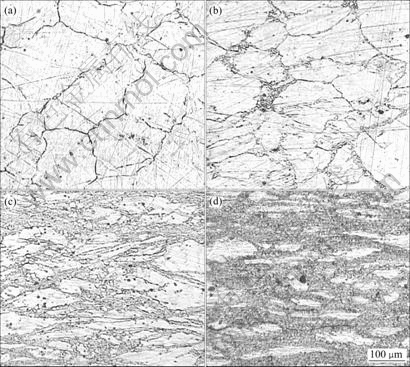
ε: (a) 0.12; (b) 0.24; (c) 0.60; (d) 0.93
图2 ZK60镁合金在温度为623 K和应变速度为0.1 s-1条件下变形组织随应变量ε演变的金相组织形貌
Fig.2 Microstructure evolutions of ZK60 alloy deformed at 623 K and 0.1 s-1
动态再结晶的晶粒粒径主要取决于热加工的流变应力σ [4]：
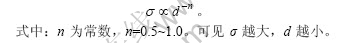
结合上述实验结果，该合金在573~723 K热加工时，提高变形速率或降低变形温度有利于在动态再结晶后获得粒径较小的晶粒。
综合以上分析可知，若使该合金在较小的应变量下迅速发生动态再结晶，以期减少变形抗力，则应选择低变形速率或高变形温度；若用热加工来细化晶粒，则适宜选择高变形速率或低变形温度。因此，在制定该合金挤压工艺时，若因设备等原因无法减小变形速率时，则应选择在较高温度下挤压；若侧重考虑提高合金热加工后力学性能和减少热裂倾向，则应选择在较低温度下挤压。综合以上因素，选择在623~673 K温度下进行挤压，制备出棒状试样。
2.2 合金高温(573~723 K)塑性变形材料参数及Zener-Hollomon本构关系的确定
由实验结果可知，Mg-5.3Zn-0.8Zr合金的流变应力、应变速率和温度之间存在明显的相互关系，因此有必要明确合金塑性变形行为中各因素之间的相关性，从而掌握合金高温塑性变形行为，并为数值模拟研究提供依据。
材料在高温蠕变时，稳定流变应力σ和应变速率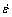
服从如下关系：
它反映高温塑性变形时应变硬化与动态软化过程之间的平衡关系。
常数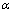
，
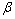和n之间存在如下关系：
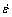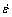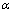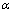利用ln-lnσ和ln-σ曲线的线性关系(如图3(a)和(b)所示)，线性回归求出n和β，并由式(2)确定。这里求得=0.017 561 MPa-1。然后，由式(1)转化成如下线性关系：
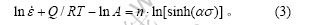
(a) 不同温度下ln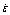
-lnσ关系; (b) 不同温度下ln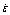-σ关系; (c) 不同温度下ln-
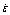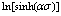关系;
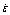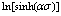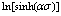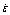(d) 不同时-T关系; (e) 不同温度下n-ln关系
图3 合金高温塑性变形峰值应力σ与应变速率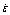及温度T的关系
Fig.3 Relationship between strain rate 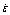and temperature T as a function of peak stress σ of high temperature plastic deformation
即可求出n和Q：
式中：n为图3(c)中ln-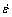
直线斜率，即为应力指数；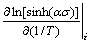
可由-1/T直线斜率确定，如图3(d)所示。
应力指数n和变形激活能Q的理论计算值见表1。由表1可见，n随着变形温度升高而增加，而且增加的幅度逐渐增大。Q与镁的晶格自扩散激活能(135 kJ/mol)的比值最低为0.93，最高达到1.48。
表1 采用Zener-Hollomon参数法求得的Mg-5.3Zn-0.8Zr镁合金高温变形材料参数
Table 1 Apparent activation energy Q and stress exponent n of Mg-5.3Zn-0.8Zr alloy
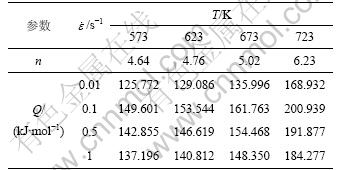
图4所示为实验所求变形激活能Q与温度T及应变速率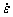
的关系。从图4可以看出，该合金的变形激活能随着温度升高而增加，而且增加的幅度越来越大，特别是当温度超过673 K时，变形激活能随温度升高而迅速升高；而其随应变速率的变化规律则比较复杂，当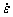小于0.1 s-1时，Q随着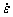的增大而增大；当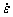大于0.1 s-1时，Q随着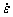的增大反而减小。这说明在一定温度和应变速率范围内，该合金的热变形机制可能有所不同。
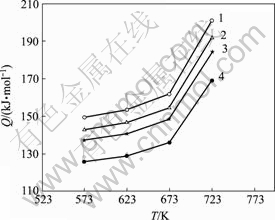
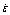/s-1: 1—0.10; 2—0.50; 3—1.00; 4—0.01
图4 不同应变速率下变形激活能与温度的关系
Fig.4 Apparent activation energy of alloy as a function of temperature at different strain rates
变形激活能随变形温度的升高而增加，可能与动态再结晶对大量位错的消耗有关。动态再结晶的形成和长大需要消耗大量的位错，随着变形温度升高，动态再结晶更加强烈，位错消耗倾向增强，应力集中得到松弛，从而潜在位错源数量减少并且启动更加困难，这将导致变形激活能增大。在温度超过673 K时，由于位错攀移机制[8]，使上述过程更为强烈，所以，变形激活能超过673 K后迅速升高。
结合式(1)引入温度补偿应变速率[13, 15-16]即Zener-Hollomon参数Z：
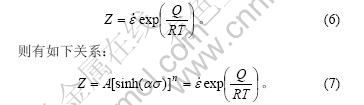
n-ln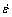关系见图3(e)，该直线截距即为Q/(RT)-lnA。将Q，R和T代入即可得到：A = 4.663 67×1012 s-1。
根据正弦双曲线反函数定义，可获得σ与Z之间的关系式：
高温稳态流变应力对应变不敏感，因此，忽略应变的影响，将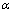和n的平均值代入式(8)可得用Z参数表示的峰值应力σ、应变速率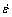和温度T的本构关系式：
3 结 论
a. 在本文实验条件内，Mg-5.3Zn-0.8Zr镁合金在热加工过程中的真应力-真应变曲线为动态再结晶型，并且随着变形速率减小或变形温度升高，峰值流变应力及其所对应的应变值均降低；合金在高温(573~723 K)变形时比在中温(473~573 K)变形时对应变速率更为敏感。
b. 在573~723 K时，应力指数n随着变形温度升高而增加，而且增加的幅度逐渐增大。
c. 当温度为573~723 K，应变速率为0.01~1.00 s-1时，Mg-5.3Zn-0.8Zr合金的变形激活能Q随温度和应变速率的改变而发生变化，Q与镁的晶格自扩散激活能(135 kJ/mol)的比值最低为0.93，最高达到1.48。
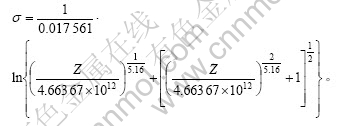
d. 采用Zener-Hollomon参数法构建的Mg-5.3Zn- 0.8Zr镁合金高温塑性变形峰值应力σ、应变速率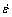和温度T之间的本构关系为：
。
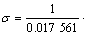
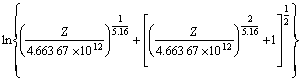其中：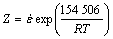
。
参考文献：
[1] Decker R F. The renaissance in magnesium[J]. Advanced Mater & Proc, 1998, 18(9): 31-35.
[2] Froes F H, Eliezer D, Aghion E. The science, technology and applications of magnesium[J]. JOM, 1998, 20(9): 30-33.
[3] Ion S E, Hunphreys F J. Dynamic recrystallisation and the development of microstructure during the high temperature deformation of magnesium[J]. Acta Mater, 1982, 30(12): 1909-1912.
[4] 唐仁正. 物理冶金基础[M]. 北京: 冶金工业出版社, 1997: 89-100.
TANG Ren-zheng. Physical metallurgy foundation[M]. Beijing: Metallurgy Industry Press, 1997: 89-100.
[5] 刘 正, 张 奎, 曾小勤. 镁基轻质合金理论基础及其应用[M]. 北京: 机械工业出版社, 2002: 145-178.
LIU Zheng, ZHANG Kui, ZENG Xiao-qi. Theoretical basis and application of magnesium-base lightweight alloy[M]. Beijing: China Machine Industry Press, 2002: 145-178.
[6] Mukai T, Yamanoi M, Watanabe H. Effect of grain refinement on tensile ductility in ZK60 magnesium alloy under dynamic loading[J]. Materials Transactions, 2001, 10(42): 1177-1181.
[7] Watanabe H, Mukai T J, Mabuchi M. High-strain-rate superplasticity at low temperature in a ZK61 magnesium alloy produced by powder metallurgy[J]. Scripta Materialia, 1999, 21(41): 209-213.
[8] Galiyev A, Kaibyshev R. Correlation of plastic deformation and dynamic recrystallization in magnesium alloy ZK60[J]. Acta Mater, 2001, 23(49): 1199-1207.
[9] 余 琨. 稀土变形镁合金组织性能及加工工艺研究[D]. 长沙: 中南大学材料科学与工程学院, 2002.
YU Kun. Effects of rare earth on microstructure and mechanical properties of wrought magnesium alloy[D]. Changsha: School of Materials Science and Engineering, Central South University, 2002.
[10] 郭 强, 严红革, 陈振华, 等. AZ31镁合金高温热压缩变形特性[J]. 中国有色金属学报, 2005, 15(6): 900-904.
GUO Qiang, YAN Hong-ge, CHENG Zhen-hua, et al. Hot compression deformation behavior of AZ31 magnesium alloy at elevated temperature[J]. The Chinese Journal of Nonferrous Metals, 2005, 15(6): 900-904.
[11] 刘志义, 叶呈武, 张 坤, 等. ZK31+0.3Yb镁合金的热力模拟[J]. 中南大学学报: 自然科学版, 2005, 36(6): 933-935.
LIU Zhi-yi, YE Cheng-wu, ZHANG Kun, et al. Thermal mechanical simulation of ZK31+0.3Yb magnesium alloy[J]. Journal of Central South University: Science and Technology, 2005, 36(6): 933-935.
[12] Galiyev A, Sitidikov O, Kaibyshev R. Deformation behavior and controlling mechanisms for plastic flow of magnesium and magnesium alloy materials[J]. Materials Transactions, 2003, 44(4): 426-431.
[13] Bussiba A, Artzy A B, Shtechman A. Grain refinement of AZ31 and ZK60 Mg alloys—Towards superplasticity studies[J]. Materials Science and Engineering A, 2001, 302(15): 56-62.
[14] 毛卫民, 赵新兵. 金属的再结晶与晶粒长大[M]. 北京: 冶金工业出版社, 1994: 46-87.
MAO Wei-min, ZAO Xin-bin. Recrystallization and grain growth of metal[M]. Beijing: Metallurgy Industry Press, 1994: 46-87.
[15] Poirier J P. Crystal plastic deformation at elevated temperatures[M]. Xiao Hui. Dalian: Dalian University of Technology Press, 1989: 45-76.
[16] Takuda H. Modelling on flow stress of Mg-Al-Zn alloys at elevated temperatures[J]. Journal of Materials Processing Technology, 1998, 8(18): 513-516.
收稿日期：2008-04-17；修回日期：2008-07-20
基金项目：湖南省科技攻关项目(04GK1008-2)
通信作者：易丹青(1954-)，男，湖南湘乡人，博士生导师，教授，从事高强韧铝、镁合金研究；电话：0731-8830263；E-mail: yioffice@mail.csu.edu.cn
