DOI: 10.11817/j.issn.1672-7207.2015.05.036
非饱和黄土的结构性与强度特性的关系
张宁宁,骆亚生
(西北农林科技大学 水利与建筑工程学院,陕西 杨凌,712100)
摘要:根据原状黄土、重塑黄土和饱和重塑黄土的应力-应变曲线对比,定义黄土结构强度势参数η。通过三轴试验探讨不同围压和含水率对土体结构强度势参数的影响,研究土体结构强度势参数与其抗剪强度指标之间的关系。研究结果表明:围压和含水率是影响土体结构性的2个主要因素,结构强度势参数随不同围压的变化曲线均处在一较狭窄的条带范围内,具有很好的归一性,结构强度势参数随含水率的增大而减小;土体结构强度势参数随着轴向应变的增长先线性增长在达到峰值后又呈指数形式迅速衰减;结构强度势参数与黏聚力具有指数关系,结构强度势参数与内摩擦角具有线性关系;考虑结构强度势参数的抗剪强度准则可以全面地反映具有结构性土体的强度特性,比莫尔-库仑强度准则更符合实际工程。
关键词:非饱和黄土;结构强度势参数;抗剪强度;围压;含水率
中图分类号:TU444 文献标志码:A 文章编号:1672-7207(2015)05-1838-07
Relationship between structure and strength property of unsaturated loess
ZHANG Ningning, LUO Yasheng
(College of Water Resources and Architectural Engineering, Northwest A & F University, Yangling 712100, China)
Abstract: Based on the stress-strain curves of undisturbed loess, disturbed loess and saturated disturbed loess, structural parameter η was defined. The effect of confining pressure and moisture content on structural parameter was analyzed, and the relationship between structural strength potential parameter and shearing strength parameter was discussed. The results indicate that the structure of loess is mainly affected by confining pressure and moisture content. The relationship curves between structural strength potential parameter and confining pressure have the very good normalization in a relatively narrow band range. The water content of loess is larger, and its structure parameter’ peak is stronger. The structure parameter increases linearly, then reaches the peak, and later decreases exponentially with the increment of strain. The relationship between structural strength potential parameter and cohesion is exponential and the structural strength potential parameter is linearly related to internal friction angle. The shear strength criterion, which considers structural strength potential parameter, comprehensively specifies strength property of structural soil, and it is superior to Mohr-Coulomb strength criterion, and more in line with actual engineering.
Key words: unsaturated loess; structural strength potential parameters; shear strength; confining pressure; moisture content
土体的结构是其强度、变形的内在因素。土的结构性是指构成土体的颗粒的形状、大小、表面特征、定量的比例关系、空间上的排列以及骨架颗粒的胶结形式,孔隙的形态、大小、数量以及分布情况等[1]。
原状黄土在沉积过程中形成了大孔隙骨架结构,颗粒间接触点处经过长期的物理化学作用而逐渐形成了胶结。同时,由于比较特殊的粒状架空体系和颗粒间的联结强度[2],从而也使原状黄土具有结构性和结构强度,在力学性质上表现为土体保持原结构状态不被破坏的能力[3]。土的结构性对土工程性质的重要性已成为共识,被认为是“21世纪土力学的核心问题”[4]。土结构性研究分为3种途径:细观形态学途径、固体力学途径和土力学途径。谢定义等[5]以原状土、重塑土和饱和土的应变为基础提出了基于释放土体结构势思想确定土体结构的定量化参数(基于应变考虑的结构性参数),该方法能够定量揭示土结构性及其变化的力学效果,而比定性显示土结构性的形象特征或从个别侧面定量描述土结构性的差异更具有优越性。骆亚生等[6-7]基于三轴试验提出了反映黄土结构性的应变综合结构势参数,建立了对应于复杂应力条件的土结构性本构模型。陈存礼等[8]根据同一压力下原状、重塑和饱和黄土的孔隙比定义了一个定量结构性参数,研究了结构性参数随压力和含水率变化的规律性。邵生俊等[9-10]提出了基于应力考虑的结构性参数,并将结构性参数引入到原状黄土的应力-应变关系分析中,建立了非饱和湿陷性黄土的本构模型。冯志焱等[11-12]根据原状土体、重塑土体和饱和原状土体的试锥入土深度提出了试锥下沉结构性参数,通过试验证明了结构性定量化参数能够描述土由初始物理状态到等向应力条件下再到偏压剪切条件下的全过程中,土结构性变化的连续性。田堪良等[13-14]提出黄土的结构强度就是由联结结构强度和摩擦结构强度组成的。因此,本文作者以陕西杨凌原状黄土、重塑黄土和饱和重塑黄土作为研究对象,通过三轴剪切试验,对其在不同含水率和围压下结构性变化特性及其与强度特性关系进行研究。
1 试验方法
试验所用黄土土样均取自陕西杨凌渭河Ⅱ级阶地,取土深度为4.0 m,属于Q3黄土。试验土样的物理性质指标见表1。
为保证试验成果的可靠性和试验数据的可比性,试验制备过程严格遵守文献[15]的要求。原状土的取土、运输和制备时要尽量减少人为对土体的扰动。将现场取回的原状土样分别制成不同含水率的原状试样和相应的(同含水率、同密度)重塑试样以及相应的(同密度)饱和重塑试样。
制备重塑试样时,先将土样碾碎、过筛、拌匀,充分破坏土样的天然结构,然后按所需含水率均匀加水搅拌,保湿静置24 h,分层压实至要求的密度(天然干密度),要求试样的含水率和密度的制样相对误差不超过1%。所制备的土样初始含水率w分别为9.89%,13.05%,15.61%,18.77%,21.49%以及饱和状态共6种;饱和试样采用抽气饱和的方法进行饱和。
为保证试样中的水分均匀,将制好的试样放入养护缸中静置48 h。试验时初始固结围压σ3分别为100,200和400 kPa,试验采用固结不排水(CU),剪切速率为0.02 mm/min。
2 结构强度势参数及其变化规律
2.1 结构强度势参数定义
谢定义等[5]认为扰动、加荷和浸水是改变原状土结构的主要作用,通过重塑、扰动和浸水饱和可使原状土的结构势充分释放出来,因此,在三轴仪上分别对原状土、重塑土以及饱和重塑土进行剪切试验所得到的应力-应变曲线的形状如图1所示。图中q0,qr以及qs分别为某一轴向应变ε1下原状土、重塑土和饱和重塑土的强度(σ1-σ3)。当轴向应变ε1相同时,原状黄土的强度q0最大,饱和重塑土的强度qs最小,重塑土的强度qr在二者之间。
(q0-qr)反映了原状黄土的联结结构的强度,以联结结构强度势参数η1来反映原状黄土联接结构性的强弱(η1=(q0-qr)/qs)。η1越大,表明原状黄土的联结结构性愈强,联结结构被完全扰动后的强度损失越大。
(qr-qs)反映了重塑黄土遇水后结构的弱化和结构强度的损失,以摩擦结构强度势参数η2来反映重塑黄土摩擦结构性的强弱(η2=(qr – qs)/qs)。η2越大,表明重塑黄土的摩擦结构性愈强,摩擦结构愈水弱化后强度损失越大。
表1 陕西杨凌土样的物理性质指标
Table 1 Index of physical property of soil samples in Yangling of Shanxi


图1 三轴试验时原状土、重塑土和饱和重塑土的应力-应变曲线
Fig. 1 Relation curves of stress and strain for intact, disturbed soil and saturated disturbed soil under triaxial test condition
黄土的结构强度是由黄土颗粒之间的联结结构强度和摩擦结构强度组成。因此,可以用黄土的联结强度势η1与摩擦结构强度势η2之商即结构强度势参数η=η1/η2来反映黄土总的结构强度势。η既包含了黄土的联结结构强度势,又包含了黄土的摩擦结构强度势,综合反映了黄土的结构性强弱,可以作为一个定量描述黄土结构性的参数。
 (1)
(1)
由式(1)可知:η为q0,qr以及qs的函数,即η=f(q0,qr,qs)。其中,q0,qr以及qs又随应变ε1的不同而不同,即q0=f(ε1),qr=f(ε1),qs=f(ε1)。
2.2 结构强度势参数变化规律
试验结果表明,原状黄土的应力-应变曲线有软化型也有硬化型,试样在低含水率和低围压下呈现应变软化型,随着试样含水率和围压的增大,其应力-应变曲线呈现硬化型,其主要原因是较高的含水率和较大的围压破坏了原状土的结构性,当含水率较高和围压较大时,土体的结构性遭受严重破坏,其应力-应变曲线呈现硬化型。重塑黄土的应力-应变曲线均呈硬化型。因此,在研究黄土的结构强度势参数时,将初始含水率和初始固结围压作为影响因素考虑在内很有必要。
2.2.1 结构强度势参数与初始固结围压的变化规律
图2所示为不同初始含水率下结构强度势参数与不同初始固结围压的变化规律。从图2可以看出:结构强度势参数η具有峰值ηmax,其峰值所对应的轴向应变ε1在1%附近,记为εηmax。当轴向应变ε1小于εηmax时,结构强度势参数η随轴向应变ε1的增大呈线性增大;当轴向应变ε1大于εηmax时,结构强度势参数η随轴向应变ε1的增大反而减小,并呈指数形式迅速减小,最后趋于0;这表明土体的结构性在变形的初期对土体的特性影响较大,随着轴向应变ε1的增长其影响越来越小;出现ηmax说明土体具有一定的结构调整与压密效果,在压力较小时,处于结构压密阶段,随着压力的增长,土体的初始结构因土颗粒的调整压密而使结构性参数逐渐增大,当压力增大到一定值时,处于结构性破坏阶段。压力的增大使土体的结构性逐渐发生破坏,结构性参数降低,孔隙比也降低,压缩性较大。从图2还可以看出:在相同含水率下,结构强度势参数η随围压的变化呈规律性变化,结构强度势参数η随轴向应变ε1的变化曲线均处在一较狭窄的条带范围内,即结构强度势参数η对不同围压有较好的归一性。
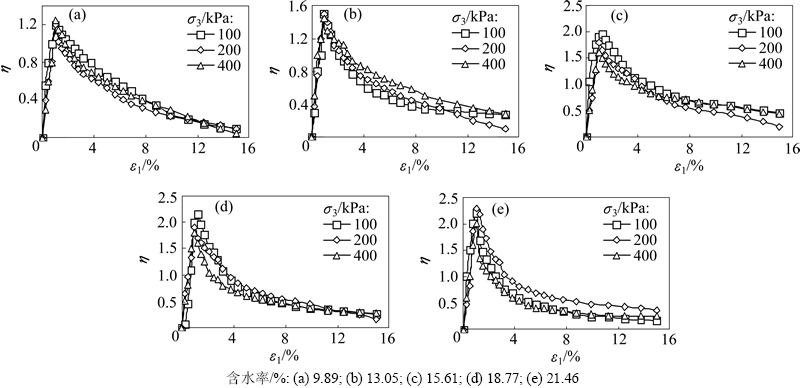
图2 土体结构强度势参数η与围压σ3的关系
Fig. 2 Relationship between structural strength potential parameter η and confining pressure σ3 of loess
2.2.2 结构强度势参数与初始含水率的变化规律
图3所示为不同初始固结围压下结构强度势参数与不同初始含水率的变化规律。从图3可以看出:不同初始含水率的试样在相同固结围压时的土体结构强度势参数η随着轴向应变ε1的变化规律相似,都是先呈线性增大,达到峰值ηmax后又以指数形式迅速减小。但土体的结构强度势参数峰值ηmax随着含水率的变化比随围压的变化更加明显,ηmax随着含水率的增加而减小。这是由于土体在含水率较小时,土体颗粒之间的摩擦力很大,摩擦强度也很大,在较小的力作用下,结构难以被破坏,随着轴力的增大,结构才逐渐破坏,摩擦结构强度才逐渐发挥出来,土体的结构强度势参数随着含水率的增加而减小。
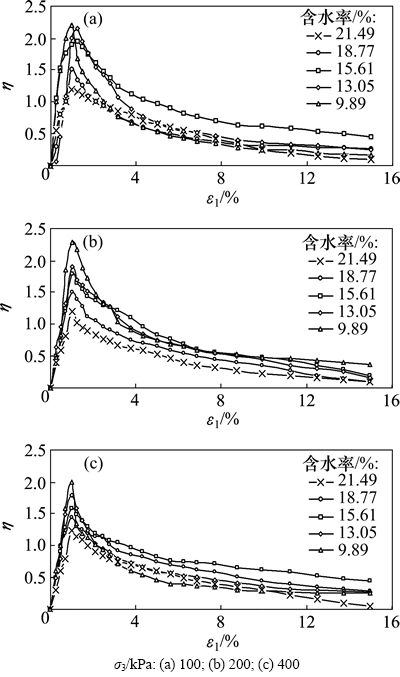
图3 土体结构强度势参数η与含水率w的关系
Fig. 3 Relationship between structural strength potential parameter η and moisture content w of loess
不同围压下的结构强度势参数ηmax与不同含水率的关系曲线如图4所示。从图4可以看出:结构强度势参数ηmax随含水率的变化有明显变化规律,ηmax随含水率的减小而增大,具有很好的线性关系,相关系数R2在不同围压下均接近于1。围压对土体结构性的影响没有含水率对其影响明显。

图4 在不同围压下土体结构强度势参数ηmax与含水率w的变化关系
Fig. 4 Relationship between structural strength potential parameter ηmax and moisture content w under different confining pressures of loess
2.3 结构强度势参数与抗剪强度关系分析
天然沉积的原状黄土表现出显著的结构性;通过扰动、加荷和浸水等方式可使原状土的结构势充分释放出来。原状土的应力-应变曲线既有软化型又有硬化性,重塑土的应力-应变曲线均为硬化型;土体在剪切过程中,伴随着土结构的破损,黄土所表现出抵抗变形的能力将逐渐减弱,其强度也将发生明显变化。在剪切变形初期(ε1<εηmax),结构强度势参数随应变的增长而增大,土体抵抗剪切破坏的能力仍增强;当土体承受的剪切应力达到峰值后,随着变形的增加,其结构强度势参数呈衰减趋势,与抗剪强度的衰减一致。可见:土体的抗剪强度与其结构性有密切关系,不同结构性的土的抗剪强度不同,结构性的增长与衰减过程伴随着土体抗剪强度的充分发挥和衰减。由于软化型应力-应变曲线在峰值处强度充分发挥;硬化型应力-应变曲线在剪切破坏时强度充分发挥。因此,依据土体不同的结构强度势参数对应强度的试验结果(见表2),可以分析土体结构强度势参数与其抗剪强度指标的关系。
表2 土体结构强度势参数与其抗剪强度试验结果
Table 2 Test results of structural strength potential parameter and shearing strength parameter of loess

结构强度势参数 与黄土抗剪强度指标黏聚力c、内摩擦角φ的关系如图5和6所示。由图5可以看出:土体结构强度势参数
与黄土抗剪强度指标黏聚力c、内摩擦角φ的关系如图5和6所示。由图5可以看出:土体结构强度势参数 随黏聚力c呈指数关系,
随黏聚力c呈指数关系, 与原状土黏聚力c的关系可表述为式(2),其相关系数R2为0.997 9;
与原状土黏聚力c的关系可表述为式(2),其相关系数R2为0.997 9; 与重塑土黏聚力c的关系可表述为式(3),其相关系数R2为0.992 1;由图6可以看出:土体结构强度势参数
与重塑土黏聚力c的关系可表述为式(3),其相关系数R2为0.992 1;由图6可以看出:土体结构强度势参数 随内摩擦角φ呈线性关系,
随内摩擦角φ呈线性关系, 与原状土内摩擦角φ的关系可表述为式(4),其相关系数R2为0.963 9;
与原状土内摩擦角φ的关系可表述为式(4),其相关系数R2为0.963 9; 与重塑土内摩擦角φ的关系可表述为式(5),其相关系数R2为0.984 2;由此可见:土体结构强度势参数η与其抗剪强度指标黏聚力c、内摩擦角φ有密切关系。
与重塑土内摩擦角φ的关系可表述为式(5),其相关系数R2为0.984 2;由此可见:土体结构强度势参数η与其抗剪强度指标黏聚力c、内摩擦角φ有密切关系。

图5 土体结构强度势参数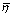 与黏聚力c的关系
与黏聚力c的关系
Fig. 5 Relationships structural parameters 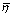 and cohesion c of loess
and cohesion c of loess

图6 土体结构强度势参数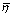 与内摩擦角φ的关系
与内摩擦角φ的关系
Fig. 6 Relationship between sructural parameters 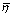 and internal friction angle φ of loess
and internal friction angle φ of loess
 (2)
(2)
 (3)
(3)
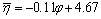 (4)
(4)
 (5)
(5)
土的抗剪强度准则是由莫尔-库仑提出,并在土力学中得到了广泛应用,但其由于土体的结构性强度是变化的,即呈非线性。因此,线性的莫尔-库仑准则对具有结构性的土体不再完全适用。所以,本文拟将土体结构强度势参数η引入莫尔-库仑准则中,以此来反映结构性土的强度特征。考虑结构性影响的抗剪强度公式可表述为
 (6)
(6)
式(6)将土体的抗剪强度表述成结构强度势参数的函数,通过强度参数与结构强度势参数之间的关系来描述具有结构性土体的强度特征。另外,结构强度势参数已经考虑了土体初始含水率、初始固结围压的影响,因此,这种表达方式可以全面地反应具有结构性土体的强度特性。将式(2)和(4)以及式(3)和(5)分别代入式(6)中得到原状土考虑土体结构性的抗剪强度公式(式(7))和重塑土考虑土体结构性的抗剪强度公式(式(8))。式(7)和式(8)中不再用 ,而用η代替
,而用η代替 ,因为η是随σ变化而变化的。
,因为η是随σ变化而变化的。
 (7)
(7)
 (8)
(8)
将计算值与试验值进行对比分析,见图7和图8。由图7和图8可以看出:考虑土体结构性的抗剪强度公式计算值不再符合直线规律,而是呈曲线变化,这与土体的实际受力过程相符合,更有助于实际工程意义。

图7 原状土抗剪强度包线计算值与试验值
Fig. 7 Calculated values and trial values of shear strength envelope of undisturbed soil

图8 重塑土抗剪强度包线计算值与试验值
Fig. 8 Calculated values and trial values of shear strength envelope of disturbed soil
3 结论
1) 黄土的结构强度是由黄土颗粒之间的联结结构强度和摩擦结构强度组成。通过原状非饱和黄土、重塑黄土以及饱和重塑黄土的应力-应变关系对比,定义了结构强度势参数η,为研究非饱和黄土结构提供了新的途径。
2) 土体结构强度势参数随着土体轴向应变的增长分为2个阶段:第1阶段,当ε1<εηmax时,土体结构强度势参数随轴向的应变的增长呈线性迅速增长,直到达到峰值ηmax,此时εηmax接近于1%;第2阶段,当ε1>εηmax时,土体结构强度势参数随轴向的应变的增长呈指数形式迅速减小。
3) 在相同含水率下,结构强度势参数η随围压的变化呈规律性变化,结构强度势参数η随轴向应变ε1的变化曲线均处在一较狭窄的条带范围内,即结构强度势参数η对不同围压有较好的归一性;在相同围压下,结构强度势参数随土体含水率的增加而减小,由于土体在含水率较小时,黄土颗粒之间的摩擦力很大,摩擦结构强度势较大。
4) 土体结构强度势参数 与其抗剪强度指标c具有指数关系;土体结构强度势参数
与其抗剪强度指标c具有指数关系;土体结构强度势参数 与其抗剪强度指标φ具有线性关系;通过将土体结构强度势参数引入到莫尔-库伦强度准则中可以全面地反映具有结构性土体的强度特性,含有结构性参数的强度准则不再符合线性关系,而是呈曲线形式,这与土体的实际受力过程相符合。
与其抗剪强度指标φ具有线性关系;通过将土体结构强度势参数引入到莫尔-库伦强度准则中可以全面地反映具有结构性土体的强度特性,含有结构性参数的强度准则不再符合线性关系,而是呈曲线形式,这与土体的实际受力过程相符合。
参考文献:
[1] 齐吉琳. 土的结构性及其定量化参数的研究[M]. 西安: 西安理工大学出版社, 1999: 15-20.
QI Jilin. Research of structural and quantitative parameter of soil[M]. Xi’an: Xi’an University of Technology Press, 1999: 15-20.
[2] 高国瑞. 黄土湿陷变形的结构理论[J]. 岩土工程学报, 1990, 12(4): 1-10.
GAO Guorui. A structure theory for collapsing deformation of loess soils[J]. Chinese Journal of Geotechnical Engineering, 1990, 12(4): 1-10.
[3] 骆亚生, 张爱军. 黄土结构性的研究成果及其新进展[J]. 水力发电学报, 2004, 23(6): 66-69.
LUO Yasheng, ZHANG Aijun. Outcomes research ofloess and its new advance[J]. Journal of Hydroelectric Engineering, 2004, 23(6): 66-69.
[4] 沈珠江. 土体结构性的数学模型: 21世纪土力学的核心问题[J]. 岩土工程学报, 1996, 18(1): 95-97.
SHEN Zhujiang. The mathematical model for the structured soils: The key problem of soil mechanics in 21th century[J]. Chinese Journal of Geotechnical Engineering, 1996, 18(1): 95-97.
[5] 谢定义, 齐吉琳. 土结构性及其定量化参数研究的新途径[J]. 岩土工程学报, 1999, 21(6): 651-656.
XIE Dingyi, QI jilin. Soil structure characteristics and new approach in research on its quantitative parameter[J]. Chinese Journal of Geotechnical Engineering, 1999, 21(6): 651-656.
[6] 骆亚生, 谢定义, 邵生俊, 等. 复杂应力条件下的土结构性参数[J]. 岩石力学与工程学报, 2004, 23(24): 4248-4251.
LUO Yasheng, XIE Dingyi, SHAO Shengjun, et al.Soil structural parameters under complex stress conditions[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(24): 4248-4251.
[7] 骆亚生, 谢定义. 复杂应力条件下土的结构性本构关系[J]. 四川大学学报(工程科学版), 2005, 37(5): 14-18.
LUO Yasheng, XIE Dingyi. Structural constitutive relation of soils under complex suess conditions[J]. Journal of Sichuan University (Engineering Science Edition), 2005, 37(5): 14-18.
[8] 陈存礼, 胡再强, 高鹏. 原状黄土的结构性及其与变形特性关系研究[J]. 岩土力学, 2006, 27(11): 1891-1896.
CHEN Cunli, HU Zaiqiang, GAO Peng. Structural and deformation characteristics of undisturbed loess[J]. Rock and Soil Mechanics, 2006, 27(11): 1891-1896.
[9] 邵生俊, 周飞飞, 龙吉勇. 原状黄土结构性及其定量化参数研究[J]. 岩土工程学报, 2004, 26(4): 531-536.
SHAO Shengjun, ZHOU Feifei, LONG Jiyong. Study of the structural and quantitative parameters of undisturbed loess[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(4): 531-536.
[10] 邵生俊, 龙吉勇, 于清高, 等. 湿陷性黄土的结构性参数本构模型[J]. 水利学报, 2006, 37(11): 1315-1322.
SHAO Shengjun, LONG Jiyong, YU Qinggao, et al. A constitutive model of collapsible loess with structural parameter[J]. Journal of Hydraulic Engineering, 2006, 37(11): 1315-1322.
[11] 冯志焱. 非饱和黄土的结构性定量化参数与结构性本构关系研究[D]. 西安: 西安理工大学土木建筑工程学院, 2008: 62-68.
FENG Zhiyan. Research on soil structural parameters and structural constitutive model of unsaturated loess[D]. Xi’an: Xi’an University of Technology. School of Civil Engineering and Architecture, 2008: 62-68.
[12] 冯志炎, 谢定义. 复杂加载条件下原状黄土结构性定量化参数变化全过程分析[J]. 西安理工大学学报, 2009, 25(1): 72-75.
FENG Zhiyan, XIE Dingyi. Quantitative analysis of soil structure variations in whole process under complex loading conditions of intact loess[J]. Journal of Xi’an University of Technology, 2009, 25(1): 72-75.
[13] 田堪良. 黄土的结构性及其结构性本构关系研究[D]. 南京: 河海大学土木交通学院, 2009: 32-35.
TIAN Kanliang. Research on structural and structural constitutive of soil[D]. Nanjing: Hohai University. College of Civil and Transportation Engineering, 2009: 32-35.
[14] 田堪良, 张慧莉, 马俊. 基于强度条件的黄土结构性静力试验研究[J]. 岩土力学, 2012, 33(7): 1993-1994.
TIAN Kanliang, ZHANG Huili, MA Jun. Test study of loess structure based on static strength conditions[J]. Rock and Soil Mechanics, 2012, 33(7): 1993-1994.
[15] SL 237—1999, 土工试验规程[S].SL 237—1999, Specification of soil test[S].
(编辑 赵俊)
收稿日期:2014-05-19;修回日期:2014-08-30
基金项目(Foundation item):国家自然科学基金资助项目(51178392) (Project(51178392) supported by the National Natural Science Foundation of China)
通信作者:骆亚生,教授,博士生导师,从事黄土力学与工程的研究;E-mail: 771545499@qq.com