Static compressive properties and damage constitutive model of rubber cement mortar with dry- and wet-curing conditions
来源期刊:中南大学学报(英文版)2021年第7期
论文作者:徐颖 杨荣周 陈佩圆 龚玖
文章页码:2158 - 2178
Key words:curing humidity; rubber cement mortar; uniaxial compression; cyclic loading-unloading; mesoscopic damage; constitutive model
Abstract: To investigate the static compressive properties and mechanical damage evolution of rubber cement-based materials (RCBMs) with dry- and wet-curing conditions, uniaxial compression and cyclic loading-unloading tests were carried out on rubber cement mortar (RCM). The mechanical properties of the uniaxial compression specimens cured at 95% (wet-curing) and 50% (dry-curing) relative humidities and cyclic loading-unloading specimens cured at wet-curing were analyzed. Under uniaxial compression, the peak stress loss ratio is higher for dry-curing than for wet-curing. The peak strain decreases with the increase of rubber content, and the peak strain increases with the decrease of curing humidity. Under cyclic loading-unloading, the variation trends of residual strain differences of the normal cement mortar and RCM at each cyclic level with the number of cycles are basically the same, but the failure modes are different. The analysis of the internal mesostructure by a scanning electron microscope (SEM) shows that initial damage is further enhanced by reducing curing humidity and adding rubber aggregate. The damage constitutive model based on strain equivalence principle and statistical theories was used to describe the uniaxial compression characteristics of RCM, and the law of mechanical damage evolution was predicted.
Cite this article as: YANG Rong-zhou, XU Ying, CHEN Pei-yuan, GONG Jiu. Static compressive properties and damage constitutive model of rubber cement mortar with dry- and wet-curing conditions [J]. Journal of Central South University, 2021, 28(7): 2158-2178. DOI: https://doi.org/10.1007/s11771-021-4763-1.

J. Cent. South Univ. (2021) 28: 2158-2178
DOI: https://doi.org/10.1007/s11771-021-4763-1

YANG Rong-zhou(杨荣周)1, 2, XU Ying(徐颖)1, 2, CHEN Pei-yuan(陈佩圆)2, GONG Jiu(龚玖)3
1. State Key Laboratory of Mining Response and Disaster Prevention and Control in Deep Coal Mines,
Anhui University of Science and Technology, Huainan 232001, China;
2. School of Civil Engineering and Architecture, Anhui University of Science and Technology,Huainan 232001, China;
3. Changling Petro-chemical Engineering Design Co., Ltd., Yueyang 414012, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Abstract: To investigate the static compressive properties and mechanical damage evolution of rubber cement-based materials (RCBMs) with dry- and wet-curing conditions, uniaxial compression and cyclic loading-unloading tests were carried out on rubber cement mortar (RCM). The mechanical properties of the uniaxial compression specimens cured at 95% (wet-curing) and 50% (dry-curing) relative humidities and cyclic loading-unloading specimens cured at wet-curing were analyzed. Under uniaxial compression, the peak stress loss ratio is higher for dry-curing than for wet-curing. The peak strain decreases with the increase of rubber content, and the peak strain increases with the decrease of curing humidity. Under cyclic loading-unloading, the variation trends of residual strain differences of the normal cement mortar and RCM at each cyclic level with the number of cycles are basically the same, but the failure modes are different. The analysis of the internal mesostructure by a scanning electron microscope (SEM) shows that initial damage is further enhanced by reducing curing humidity and adding rubber aggregate. The damage constitutive model based on strain equivalence principle and statistical theories was used to describe the uniaxial compression characteristics of RCM, and the law of mechanical damage evolution was predicted.
Key words: curing humidity; rubber cement mortar; uniaxial compression; cyclic loading-unloading; mesoscopic damage; constitutive model
Cite this article as: YANG Rong-zhou, XU Ying, CHEN Pei-yuan, GONG Jiu. Static compressive properties and damage constitutive model of rubber cement mortar with dry- and wet-curing conditions [J]. Journal of Central South University, 2021, 28(7): 2158-2178. DOI: https://doi.org/10.1007/s11771-021-4763-1.
1 Introduction
With the rapid development of the rubber product industry, the appropriate disposal of waste rubber worldwide has become the key to environmental protection and resource reuse. Mixing waste rubber particles into cement-based materials (CBMs) to preparing rubber cement-based materials (RCBMs) is both resource-saving and environmentally friendly [1]. Moreover, RCBMs have the advantage of being lightweight [2] and features of efficient energy dissipation [3] and fatigue [4], impact [5], and freezing resistance [6],among other properties. As we all know, a series of properties of materials fundamentally determine the field in which materials can be applied, which is the value and significance of material research, and RCBMs just reflect this point.
In fact, RCBMs have attracted the attention of scholars worldwide, and their feasibility for a wide range of engineering applications (such as anti-seismic and explosion protection) has been studied extensively [7, 8]. It is worth noting that RCBMs can be recycled as a renewable aggregate similar to ordinary CBMs, which is considered to be an effective way to reduce the exploitation of natural resources and protect the environment. For example, ASLANI et al [9] used waste recycled concrete aggregate and rubber particles to develop high-performance self-compacting concrete, and LIU et al [10] studied the fatigue properties of rubber-modified recycled aggregate concrete. Their results show that the recycled aggregate and rubber particles can improve the fatigue life of concrete, especially when the rubber particle content reaches 20%.
Although the RCBMs has many advantages, it is undeniable that rubber materials significantly weaken the strength and modulus of the CBMs, even under the standard curing conditions in the laboratory [11, 12]. In this connection, ZHANG et al [13] and ZHU et al [14] analyzed the internal microporous structures of RCBMs utilizing mercury intrusion porosimetry (MIP) and SEM. The results showed that the pore size and porosity of RCM were shown to increase with rubber content; the content of macropores (diameter d>1000 nm) increases the most, while that of gel pores (d<10 nm) does not change much, and when the rubber content is 5%, the total porosity of high-performance rubber concrete increases by 3.45% and the small pore volume of 10-100 nm is mainly controlled by rubber content. To promote the application of recycled crumb rubber concrete in civil engineering, GUO et al [15] studied the damage evolution process of recycled crumb rubber concrete (RCRC) under uniaxial compression by using a two-dimensional quantitative cloud image correlation method and a meso-numerical model on random aggregate.
Interestingly, curing conditions (such as the curing humidity) have a strong influence on the hydration products of a CBM and can play a key role in its performance [16, 17]. In this connection, specifically, dry-curing leads to an increase in the total porosity and pore volume of concrete, while it significantly reduces its compressive strength compared with wet-curing [18]. LUO et al [19] believed that this significant increase in porosity under dry-curing conditions may be due to the concrete’s loss of free water to the surrounding environment, which reduces the hydration degree of cement and the filling effect of hydration products on pores. However, inevitably, due to the variability and complexity of the actual construction environments, it is difficult to meet standard curing conditions. Therefore, initial damage inside engineering structures occurs, adversely affecting the mechanical properties and durability and causing safety hazards. To explore the effect of curing humidity on the fracture properties of concrete materials, MI et al [20] proposed a maturity model considering the coupling effect of curing temperature and humidity by introducing an innovative humidity rate function, which can accurately predict the fracture properties of concrete. SHEN et al [21] believed that the decrease of the internal relative humidity of high-performance concrete will cause autogenous shrinkage. To evaluate the cracking resistance of high-performance concrete, a relative humidity model of early-age internally cured concrete was established, and the model has good accuracy. According to the principle of humidity compensation, LYU et al [22] proposed a method to control shrinkage and anti-fracture. Finally, the enhancement mechanism of cement hydration was revealed by SEM. In addition, to study the effect of rubber content and particle size on the mechanical properties of concrete, LI et al [23] carried out uniaxial compression tests on rubber concrete and analyzed the strength, elastic modulus, peak strain, ultimate strain, the appearance of visible cracks, and the failure mode of specimens. Finally, based on the GB50010-2002 standard, a uniaxial compression constitutive model that can characterize the mechanical characteristics of low volume rubber concrete was established [23]. To study the brittle-ductile transition and mechanical properties of cement mortar, WANG et al [24] carried out a series of tests such as triaxial cyclic loading-unloading. Based on the analyses and discussions of strength and deformation characteristics, an elastic-plastic model was established by using the principle of effective stress, and the effectiveness of the model is verified by comparing the simulation results with the experimental results [24].
In this work, on the basis of the dynamic mechanics, dynamic damage, and static fracture study of normal cement mortar (NCM) and RCM by YANG et al [25, 26], we also took the NCM and RCM with 95% and 50% curing humidities as the research object and did more in-depth research and analysis on them. The specific research contents and innovations are mainly reflected in the following four aspects: 1) Through uniaxial compression tests of NCM and RCM with two different levels of curing humidity and the cyclic loading-unloading tests of NCM and RCM, the stress-strain curves, peak stress, peak strain, failure modes, and residual strain were analyzed. From the strain evolution process of the specimens under cyclic loading-loading test, it positively reflects the irreversible loading damage of the specimen under uniaxial compression; 2) Through SEM test, the mesoscopic structures and hydration product states of the specimens were observed, and the effects of curing humidity on the hydration degree, micropores, and microcracks of the matrix, as well as the effect of rubber aggregate on the matrix structure were discussed, which positively reflected the initial damage caused by the addition of rubber particles and the reduction of curing humidity; 3) According to the strain equivalence principle and from the point of view of damage energy dissipation of micro-element, a full stress-strain curve damage constitutive model was established based on material parameters obeying Weibull distribution and Lognormal distribution, which solves the problem that many damage constitutive equations can not better well describe the pre-peak initial compaction stage of the stress-strain curve; 4) Through the established damage constitutive model, the damage evolution curves of the specimens under the three damage factors of curing humidity, rubber particles, and external load were comprehensively analyzed. The experimental and theoretical results were verified, and the damage evolution characteristics of materials under uniaxial compression were effectively characterized and predicted. The study on mechanics and damage characteristics of RCM with dry- and wet-curing conditions may provide a reference point for future practical engineering applications.
2 Materials and methods
2.1 Test materials and mix proportions
Ordinary Portland cement and tap water were used in the test. Natural river sand was utilized as the fine aggregate, with a maximum particle size of 5 mm, a fineness modulus of 2.6, and a density of 2600 kg/m3. The rubber fine aggregate (20 mesh) used in the test came from waste tire rubber, and its density was 1120 kg/m3. The rubber aggregate underwent internal mixing, and volume fractions of 0%, 10%, 15%, 20%, and 30% were substituted for sand. The mix proportions of NCM and RCM specimens are listed in Table 1 [25-27].
Table 1 Mix proportions (unit: kg/m3)

2.2 Specimen preparation and test process
According to the standard for test method of performance on building mortar (JGJ/T 70-2009) [28], to test the uniaxial compression properties and damage evolution characteristics of cement mortar under standard size state, the sizes of the standard cube compression specimen for the cement mortar were 70.7 mm×70.7 mm×70.7 mm (the cement used was P.O 42.5). According to Ref. [24], to better study the mechanical properties and damage characteristics of cement mortar under cyclic loading-unloading test, cement mortar specimens with standard sizes of Φ50 mm×100 mm were selected for cyclic loading-unloading test. It should be noted that in order to ensure that the upper and lower end faces of the mortar specimen are parallel and smooth, the upper and lower end faces of the mortar specimen were polished, so the sizes of the cyclic loading-unloading specimen for the cement mortar were Φ50 mm×98 mm (the cement used was P.O 52.5). The step-by-step mixing protocol was as follows [26]: first, the fine aggregate and cement were dry-mixed for 1.5 min; then, rubber particles were added and were dry-mixed for 1.5 min until uniform, and the last step was adding water and mixing for another 1.5 min.
After stripping, the standard cube compression specimens were placed in a constant temperature ((20±2) °C) curing boxes with relative humidity levels of 95% (standard curing: wet curing) and 50% (dry curing) for 28 d. The cyclic loading-unloading specimens were cured under standard curing conditions for 28 d. There were three parallel specimens ①, ②, and ③ in each group. After curing, the specimens were air-dried naturally for 48 h using indoor ventilation to avoid the influence of internal water by keeping the same moisture content of the dry- and wet-curing specimens during the test. To ensure appropriate air drying, the specimens were kept at a distance greater than 10 cm. The standard cube compression specimens were subsequently placed on a uniaxial compression tester, and the test was carried out in a controlled-displacement loading mode with a displacement loading rate of 0.5 mm/min [26], as illustrated in Figure 1(a). For the cyclic loading-unloading test, specimens were placed on the rock mechanics test control system, and the test was carried out in a controlled-force loading mode with a force loading rate of 0.5 kN/s [24], as shown in Figure 1(b).
3 Results and analysis
3.1 Mechanical properties of specimens under uniaxial compression
Based on the uniaxial compression test, the mechanical properties of the specimens were analyzed from the perspective of stress-strain curves, peak stress, and peak strain.
According to the test data, the stress-strain curves of the specimens under static compression were obtained (see Figure 2). Figures 2(a)-(d) and show that the evolution trends for the parallel specimens are similar, indicating that the static compression properties of the material are relatively stable. It can be observed that the strength of the specimens decreases with the increase of rubber content for both dry- and wet-curing [25, 26]. Figures 2(e)-(h) reveal that the strengths of NCM and RCM decrease with the decrease of the curing humidity.
To better describe the compression failure evolution characteristics of NCM and RCM under dry- and wet-curing conditions, using NCM-0-95, 50, RCM-15-95, 50, RCM-20-95, 50, and RCM-30-95, 50 as examples. One can distinguish four evolution stages in the stress-strain curves: the initial compaction stage (OA), linear elastic stage (AB), plastic stage (BC), and post-peak failure stage (CD) (Figures 2(e)-(h)). Point D represents the ending point of the post-peak descending section of the stress-strain curve,which varies in each specimen. It can be noted that the initial compaction stage (△εOA) BC)
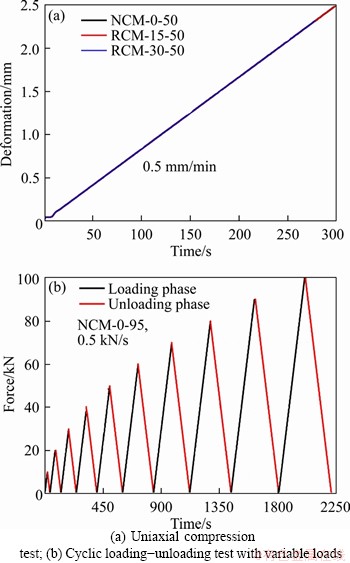
Figure 1 Test loading modes:
1) Initial compaction stage (OA). Under the external load, the specimen is first compacted due to the initial internal defects (pores and microcracks), thus the stress-strain curves have a concave trend. The compaction limit is gradually reached with the increase of load.
2) Linear elastic stage (AB). The elastic deformation occurs after the compression deformation of the defects in the specimen, which mostly conforms to Hooke’s law—the stress-strain curves increase linearly. At this point, most of the elastic strain energy accumulates in the matrix of the specimen. The elastic limit is gradually reached with the increase of load.

Figure 2 Stress-strain curves of specimens:
3) Plastic stage (BC). After the elastic deformation, the specimen enters the plastic regime. The stress growth rate decreases gradually in the BC stage, which indicates that internal damage occurs in the specimen, and part of the external force work is consumed in the form of matrix cracks. With the increase of the load, the internal damage of the specimen progressively increases, and when the stress growth rate decreases to 0, the peak-stress point is reached. It was found that, compared with wet-curing, ΔεBC with dry-curing was larger, especially reflected in RCM.
4) Post-peak failure stage (CD). Following plastic deformation, the specimen enters the post-peak failure stage, where the stress-strain curves have a decreasing trend. This indicates that a large amount of elastic strain energy and external force work is dissipated and released mainly in the form of matrix fracture, inducing internal damage in the specimens. It was found that, compared with NCM, RCM suffered a mostly ductile failure, especially reflected in dry-curing. This shows that the addition of rubber particles and the decrease of curing humidity can reduce the brittleness of cement mortar.
Furthermore, the relative change in the peak stress of specimens in the m and h groups can be expressed by the peak stress loss ratio (ρh,m):
 (1)
(1)
where σpkh and σpkm are the peak stress of the specimens in group h and group m, respectively.
It can be observed from Table 2 that, under the curing conditions of 95% and 50% relative humidities, the peak stress loss ratio of the specimens increases with the increase of the rubber content. Figure 3(a) shows that there is an ideal exponential relationship between the peak stress loss ratio and rubber content. It can be seen that the peak stress loss ratio for dry curing is slightly larger than for wet curing (see Figure 3(a)). For specimens with the same rubber content under the conditions of 95% and 50% curing humidities, Figure 3(b) shows that, there is a positive correlation between the peak stress loss ratio and rubber content. It can be observed that the peak stress loss ratio of specimens with the same rubber content due to the decrease of curing humidity increases with the rubber content (see Figure 3(b)).
Table 2 Peak stress loss ratio


Figure 3 Relationship between the peak stress loss ratios:
It is worth noting that Figure 3(a) shows that when the rubber content is 10%, the peak stress loss ratio under wet-curing is slightly greater than that under dry-curing, and both ρNCM-0-95,RCM-10-95=0.416 and ρNCM-0-50,RCM-10-50=0.413 can be regarded as basically equal. After that, the peak stress loss ratio of dry-curing is obviously higher than that of wet-curing with the increase of rubber content, which shows that rubber content is the dominant factor; when the rubber content is small, it seems that the difference and law of peak stress loss ratio between dry-curing and wet-curing can not be shown obviously. At the same time, there are some errors in this test, which is one of the reasons why the peak stress loss ratio of wet-curing is slightly higher than that of dry-curing under low rubber content.
Next, Figure 4 shows that the peak strain of the specimens decreases with the increase of rubber content for both levels of curing humidity: the fitting lines are almost parallel and follow a negative linear trend, and the peak strain increases with the decrease of the curing humidity. This shows that the decrease of curing humidity does not affect the variation of peak strain of cement mortar with rubber content while increasing the plastic deformation of cement mortar at the peak point.
3.2 Mechanical properties of specimens under cyclic loading-unloading
Based on the cyclic loading-unloading tests with variable loads, the mechanical properties of the specimens were analyzed from the perspective of stress-strain curves, failure modes, and residual strain.
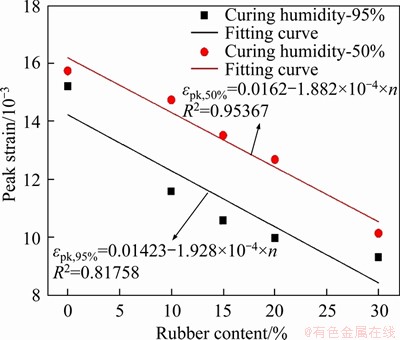
Figure 4 Relationship between peak strain and rubber content
Figure 5 represents the stress-strain curves and the failure modes of specimens NCM-0-95 and RCM-30-95 under cyclic loading-unloading tests with variable loads. The NCM-0-95 and the RCM-30-95 were loaded and unloaded to the failure endpoint, step by step under the variable load values of 10 and 5 kN, respectively. As can be seen from the figure, the stress-strain curves of the NCM-0-95 and the RCM-30-95, under cyclic loading-unloading tests with variable loads, have the same evolution characteristics (see Figure 5). Indeed, with the increase of load grade stress (σB), the load grade strain (εB) and cumulative residual strain (εC) increase in a polynomial manner, showing a trend of “fast, slow and fast” (see Figure 6), which suggests that the specimens produce irreversible plastic deformation under each loading-unloading cycle. However, an obvious difference is observed between the failure modes of the NCM-0-95 and the RCM-30-95 under cyclic loading-unloading tests with variable loads. In fact, RCM-30-95 mainly experienced shear failure in the form of principal oblique cracks of about 70° (see Figure 5(b)). However, NCM-0-95 mainly experienced conical instability failure in the form of surrounding spalling. Of course, this failure mode is also caused by shear (see Figure 5(a)).

Figure 5 Stress-strain curves and failure modes of specimens:

Figure 6 Relationship between cyclic grade strain (εB), cumulative residual strain (εC) and cyclic grade stress (σB):
Figure 7 demonstrates the changes of residual strain differences (εd=εC,i-εC,i-1, i=1, 2, ...) produced by each cyclic level of the cyclic loading-unloading tests. The residual strain differences produced by the NCM-0-95 and the RCM-30-95 are the largest at the complete failure endpoint, which are 0.0288 and 0.0431, respectively. Figures 7(b) and (c) show that the same variation trend, i.e.the increasing-decreasing-increasing trend, was observed in the residual strain differences produced by each cyclic grade of the NCM-0-95 and the RCM-30-95 under cyclic loading-unloading tests with variable loads. Combined with the stress-strain curves in Figure 5, it can be seen from Figures 7(b) and (c) that the residual strain differences produced by each cyclic level are obvious in the oa stage, indicating that it belongs to the initial compaction stage of the loading process. In the ab stage, the residual strain differences produced by each cyclic level are small and stable, indicating that it belongs to the linear elastic stage of the loading process. In the bc stage, the residual strain difference produced by each cyclic level increases rapidly, indicating that it belongs to the fracture development stage in the loading process. Therefore, the evolution trend of the stress-strain curves of the specimens under the cyclic loading-unloading tests with variable loads can be described directly through the change of residual strain differences. From the strain evolution process of the specimens under cyclic loading-loading test, it positively reflects the irreversible load damage of the specimen under uniaxial compression.
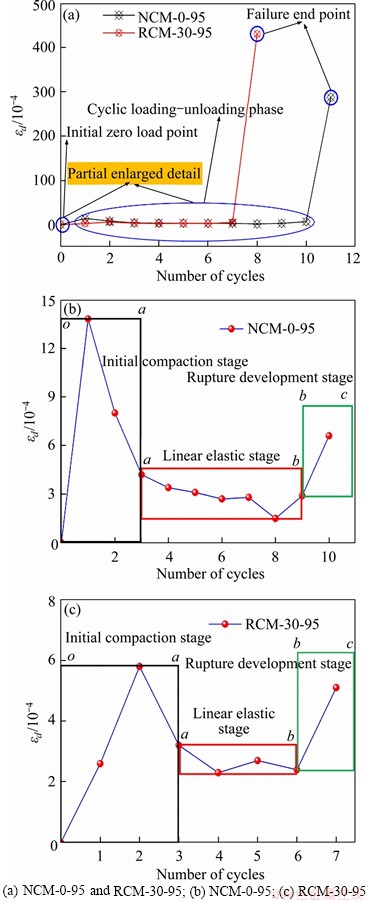
Figure 7 Relationship between residual strain differences (εd=εC,i-εC,i-1) and number of cycles:
4 Discussion on mesoscopic structure
The macroscopic damage of a CBM is essentially caused by the accumulation of mesoscopic damage in the materials [29]. In other words, the mesoscopic structure determines the macroscopic properties. However, the addition of rubber aggregates also changes the matrix structure (see Figure 8) [14, 25]. What is more, when the curing humidity is low, the hydration of the cement is incomplete, which leads to a large number of initial defects in the matrix (see Figure 9) [25, 26].
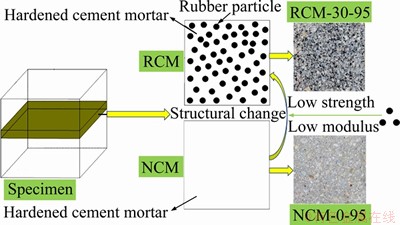
Figure 8 Schematic diagram of internal structure comparison between RCM and NCM
It can be observed in Figure 9(a) that there is no obvious fine crack and pore on the fracture surface of NCM-0-95. Upon local magnification, it finds that the structure is relatively dense. Conversely, it can be observed in Figures 9(b)-(f) that there are obvious fine cracks and pores on the fracture surfaces of NCM-0-50, RCM-15-95, 50, and RCM-30-95, 50. Upon local magnification, it finds that the structures are relatively loose. Especially, there are many fine cracks and pores (circular grooves) on the fracture surfaces of RCM-15, 30-50 (see Figures 9(d) and (f)). The above phenomena show that the initial damage of the internal structure of the cement mortar matrix will be significantly increased by adding rubber aggregate and reducing curing humidity [25, 26].
At the same time, it can be seen from Figures 9(d) and (f) that: 1) The diameters of the circular grooves are mainly in the range of 20-100 μm; 2) The surfaces of the circular grooves are relatively smooth, but there are some microcracks and pores on it. For 2), the cause of the pores is probably due to the local penetration of the contact surface caused by the upward movement of bubbles in the process of vibration and densification, and the cause of the micro-cracks is probably due to the dry-shrinkage cracking caused by the lack of moisture in the dry-curing process of the specimen [30].
In fact, due to the significant differences in the physical and chemical properties between the rubber particles and cement paste, and rubber particles do not participate in the hydration reaction in the process of cement hydration. Therefore, an interfacial transition zone (ITZ) forms at the boundaries (see Figure 10) [31] and is directly connected to the observed bonding cracks between the rubber particles and cement paste (as shown in the red mark line in Figure 9(d)). The ITZ is enlarged for low curing humidity because the surface of the rubber particles is hydrophobic [32] and the hydration reaction is incomplete. This suggests weak bonding between the cement paste and rubber particles, generating a weak interfacial zone that may act as a microcrack, which in turn leads to the initiation of the material interface crack, accelerates the failure of the matrix and explains the downward trends of the strength with the rubber content [33].
Combined with the hydration reaction mechanism of Portland cement [34], the initial damage mechanism of matrix structure caused by reducing curing humidity needs to be explained as follows from the point of view of cement hydration reaction.
After the cement is mixed with water, the clinker minerals are rapidly hydrated, resulting in a large amount of C-S-H gels, as well as Ca(OH)2 and ettringite (AFt) crystals. With further hydration reaction, the volume and number of C-S-H gel and AFt crystal are increasing, which makes the structure of hardened cement paste more compact, but C-S-H gels are the main contributor to the strength of hardened cement paste. Among them, the two main hydration reaction equations are as follows [34]:
 (2)
(2)
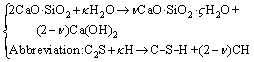 (3)
(3)
where κ is the amount of bound water; v is the ratio of calcium to silicon (C/S), which is related to temperature, water-cement ratio, and other factors.

Figure 9 Step-by-step enlarged SEM photos of fracture surface:
It can be seen from Eqs. (2) and (3) that at the initial stage of curing, when the fresh cement mortar is placed in a dry environment with a relative humidity of 50%, the free water in the fresh cement mortar will be quickly lost to the external environment, which will restrict the positive direction progress of hydration reaction greatly, resulting in the poor development of C-S-H gels, and some cement particles are likely to remain in the cement paste. Most importantly, the hydration products are stunted due to the loss of free water, so that the hydration products can not well fill the space occupied before the free water. Instead, some of the space occupied by free water is occupied by air [34]. That is to say, the decrease of curing humidity hinders the densification development of the mesostructure of hydration products, resulting in a large number of pores and microcracks in the hardened cement paste (see Figure 11). The above hydration mechanism analysis is the essential reason for the formation of pores and microcracks in cement paste.
5 Damage constitutive mode under uniaxial compression
5.1 Model establishment
According to LONG’s [35] compound damage model idea, the damage constitutive model of RCM under uniaxial compression was established considering rubber particles and dry-curing as the first stage damage and the uniaxial compression as the second stage in this study.

Figure 10 Schematic diagram of interfacial transition zone between rubber particles and cement matrix

Figure 11 Schematic diagram of meso-hydration process of cement clinker minerals under dry-curing:
5.1.1 Damage caused by rubber particles and dry-curing (initial damage)
There is some initial damage in cement mortar, such as microcracks, pores, rubber particles, and dry-curing. According to the principle of strain equivalence, the strain produced by stress on damaged materials and the strain produced by effective stress on lossless materials are equivalent [36, 37]. Combined with continuum damage mechanics (CDM), the initial damage constitutive relation of cement mortar can be modeled by the following equation:
 (4)
(4)
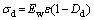 (5)
(5)
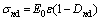 (6)
(6)
where σn is the stress on the RCM specimens with wet-curing (n=0, 10, 15, 20 and 30); σd is the stress on the specimens with dry-curing; σnd is the stress on the RCM specimens with dry-curing; E0 is the elastic modulus of NCM specimens with wet-curing (n=0); Ew is the elastic modulus of specimens with wet-curing; Dn is the damage caused by the rubber particles (n=0, 10, 15, 20 and 30); Dd is the damage caused by the dry-curing; Dnd is the damage caused by the rubber particles and dry-curing.
In the CDM, “damage” refers to the loss of mechanical stiffness, which is interpreted as the decrease of the areas, transmitting internal forces, due to the appearance and growth of micro-cracks and pores, leading to the decrease of elastic properties [38]. The experiments suggest that the rubber particles and dry-curing cause damage inside the cement mortar. According to macroscopic phenomenological damage mechanics, this damage can be characterized by the change in elastic modulus (see Figure 12). Thus, damage variables can be obtained as follows:
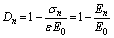 (7)
(7)
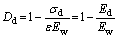 (8)
(8)
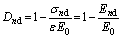 (9)
(9)
where En is the elastic modulus of the RCM specimens with wet-curing (n = 0, 10, 15, 20 and 30); Ed is the elastic modulus of the specimens with dry-curing; End is the elastic modulus of the RCM specimens with dry-curing.

Figure 12 Modulus loss caused by rubber particles (a) and dry-curing (b)
5.1.2 Damage caused by uniaxial compression (loading damage)
According to the continuum medium model, cement mortar can be regarded as being composed of countless micro-elements, and the damage of the micro-elements is directly related to the macroscopic damage of the cement mortar. It can be considered that the macroscopic failure behaviour is caused by the continuous rupture and energy dissipation of the micro-elements. The Weibull distribution is widely used in reliability engineering, especially for the distribution form of cumulative damage failure [39, 40]. Therefore, It can be assumed that the energy dissipation distribution of micro-elements in cement mortar obeys the Weibull distribution, obtaining the following probability density function [41]:
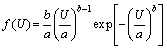 (10)
(10)
where U is the distribution variable of the micro-element energy dissipation; a and b are the distribution parameters, which are related to the physical and mechanical properties of the material.
To better analyze the damage from the perspective of energy, the cyclic loading-unloading test with equal load was carried out on the cylindrical specimen (Φ 50 mm×98 mm) RCM-15-95 (see Figure 13). Based on our results, the loading curve and unloading curve of each cycle do not coincide, which indicates that in addition to the transformation of part of the external work into elastic energy that can be released, the rest of the external work drives the material to produce plastic damage deformation and consume energy. Therefore, the ratio of damage energy density Ud to input energy density Ui under an external force can be taken as a damage variable [42]. According to the calculation principle of energy density (see Figure 13(b)), the input energy density Ui, elastic energy density Ue, and damage energy density Ud can be calculated, as follows [26, 42]:
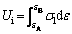 (11)
(11)
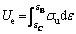 (12)
(12)
 (13)
(13)
where σl and σu are loading stress and unloading stress, respectively.
Assuming that the materials are homogeneous, continuous, and isotropic, the energy required for damage of each micro-element Udi is the same, and the input energy density and damage energy density can be calculated by Eqs. (14) and (15). Combined with probability density function, the damage variable of the material under uniaxial compression can be expressed through the ratio of the damaged number r of micro-elements to the total number j of micro-elements, Eq. (16) was obtained:
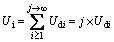 (14)
(14)
 (15)
(15)

Figure 13 Cyclic loading-unloading curves of RCM-15-95:
 (16)
(16)
where Dp is the damage caused by uniaxial compression.
5.1.3 Total damage caused by rubber particles, dry-curing, and uniaxial compression
The preliminary damage constitutive relation for RCM under uniaxial compression can be obtained as follows:
 (17)
(17)
Substituting Eq. (9) into Eq. (17) leads to [35]:
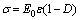 (18)
(18)
where D is the total damage caused by rubber particles, dry-curing, and uniaxial compression  .
.
Next, the D of the material under uniaxial compression can be obtained as follows:
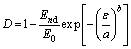 (19)
(19)
The initial constitutive relation of the material under uniaxial compression was obtained by substituting Eq. (19) into Eq. (18):
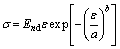 (20)
(20)
The CBMs are not completely brittle materials [43], especially the RCBMs, and they exhibit certain pre-peak initial compaction behavior and quasi-ductility or ductile fracture behavior after the peak. To effectively and accurately reproduce the compaction and fracture behaviors of these kinds of materials, the preliminary constitutive Eq. (20) obtained by using the Weibull statistical distribution theory needs to be modified.
First of all, to better characterize the full stress-strain curve and damage evolution characteristics of concrete materials under uniaxial compression, WANG [44] adopted the strain equivalence principle proposed by Lemaitre and the characteristic that material parameters obey statistical distribution. Weibull statistical distribution was used before peak strain and Lognormal statistical distribution was used after peak strain. At the same time, a damage constitutive model which can accurately describe the evolution characteristics of the full stress-strain curve of concrete materials was established by using a series of geometric boundary conditions, especially reflected in the post-peak stage of the stress-strain curve. In the study of WANG [44], the post-peak stress-strain relation was established as follows:
 (21)
(21)
Using the geometric boundary conditions: 1) 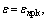
 and 2)
and 2) 
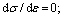 the derivative of Eq. (21) can be obtained as follows:
the derivative of Eq. (21) can be obtained as follows:
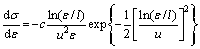 (22)
(22)
Substituting the boundary condition 2) into Eq. (22):
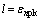 (23)
(23)
Substituting the boundary condition 1) and Eq. (23) into Eq. (21):
 (24)
(24)
Therefore, the resulting post-peak stress-strain relation is:
 (25)
(25)
Secondly, considering that there is an obvious pre-peak initial compaction stage in the stress-strain curve of RCM under uniaxial compression, it is a pity that many damage constitutive equations can not well describe this stage or directly ignore the compaction stage Figure 14(a). But at the same time, it was found that the initial compaction stage before the peak and the late softening stage after the peak approximately show symmetrical evolution characteristics in geometry, as shown in Figure 14(b). Therefore, combined with the research results of WANG [44] and the geometric symmetry similarity between pre-peak and post-peak, that is, to further better characterize the full stress-strain curve and damage evolution characteristics of materials under uniaxial compression, Eq. (25) was applied to the full stress-strain curve of materials under uniaxial compression, and Eq. (20) was further modified.
Finally, the damage constitutive model for cement mortar can be expressed as follows:
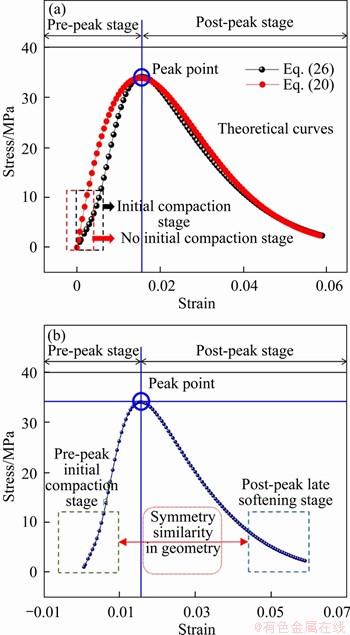
Figure 14 Difference of theoretical curves in initial compaction stage (a) and geometric symmetry similarity between pre-peak and post-peak (b)

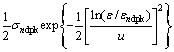 (26)
(26)
where σndpk is the peak stress of the specimens with dry-curing (n=0, 10, 15, 20 and 30); εndpk is the peak strain with dry-curing (n=0, 10, 15, 20 and 30); u is the shape control parameter, obtained by curve fitting.
5.2 Calculation and verification of model parameters
The two sides of Eq. (26) were adjusted, and the logarithm was taken to obtain the following expression:
 (27)
(27)
In the same way, Eq. (27) becomes:
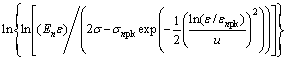
 (28)
(28)
Let x=lnε,
 ;
;
then Eq. (28) becomes:
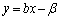 (29)
(29)
where 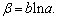
To explore the influence of a parameter, from the damage constitutive model, on the stress-strain curve characteristics, a parameter was analyzed with other parameters unchanged (see Figure 15). Figure 15(a) shows that with the increase of σpk, the initial compaction stage stays the same, while the linear elastic modulus increases. As can be seen in Figure 15(b), with the increase of εpk, the shape of the stress-strain curve changes greatly, the peak stress decreases, and the post-peak stage gradually changes to the pre-peak stage. Figure 15(c) shows that with the increase of E, the shape of the stress-strain curve changes slightly, while the peak stress increases. Figure 15(d) shows that with the increase of a, the initial compaction stage and linear elastic stage basically remain unchanged, while the peak stress and the peak strain increase, the post-peak softening rate decreases and the ductility increases. Based on Figure 15(e), with the increase of b, the initial compaction stage and linear elastic stage basically remain constant, while other factors including the peak stress, the peak strain, the post-peak softening rate, and the brittleness increase. Finally, as it can be observed in Figure 15(f) that, with the increase of u, the initial compaction stage gradually changes to the linear elastic stage, the plastic stage becomes more and more obvious, while the peak stress basically stays the same, the post-peak softening rate decreases and the ductility increases.
Table 3 contains the resulting parameters from fitting the stress-strain curves generated from the model were compared with the experiment, as shown in Figure 16. Table 3 and Figure 16 suggest that the stress-strain curves fitted by our model are consistent with the experimental data, with correlation coefficients (R-square) above 0.98. Therefore, the damage constitutive model established in this paper can accurately describe the full stress-strain relationship of RCM with dry- and wet-curing under uniaxial compression.

Figure 15 Influence of different parameters on shape of stress-strain curves:
5.3 Evolutionary characteristics of damage variables
To further elucidate the influence of rubber content and dry-curing on the damage evolution characteristics of cement mortar, the damage variables of NCM and RCM under uniaxial compression were analyzed. Because the strain rate was kept constant during the entire uniaxial compression test, the same strain process was used to calculate the damage; thus, more complete damage curves were obtained (see Figure 17). For the two curing humidity conditions, the relationships between the damage variables of the five rubber concentrations and the strain are shown in Figure 17.
Table 3 Relevant parameters of damage constitutive model


Figure 16 Comparison of damage constitutive model fitting with experimental results for:
For the two curing humidity levels, the damage variables of each group of specimens show a monotonous, approximately “S”-shaped increase with strain. When the strain reaches 0.032, the damage variables for each group are more than 0.8, and gradually approach 1 with the increase of strain. For both curing humidity levels, when the strain is 0, the corresponding initial damage value increases with rubber content. For specimens with the same rubber content, when the strain is 0, the corresponding initial damage value increases with the decrease of curing humidity.
Based on our findings, for the specimens with the same rubber content, an intersection point I is observed in the damage curves of the two curing humidity. Interestingly, during the early stage (ε<εI), the damage for each group of specimens with the same rubber content increases, when the curing humidity decreases. During the later stage (ε>εI), the damage for each group of specimens with the same rubber content decreases, when the curing humidity decreases. However, the damage values tend to be equal with the increase of rubber content. These results confirm that adding rubber particles and reducing curing humidity increases the internal damage of cement mortar. Therefore, the constitutive model damage variable proposed in this paper can accurately describe the mechanical damage evolution of RCM under uniaxial compression.
According to CDM, the “damage variable” is a measure of the degree of deterioration of a material or structure, and it is a state variable that reflects irreversible changes in the material’s structure. In practical engineering applications, it is of great significance to effectively reflect the working state of RCBMs and predict the macroscopic mechanical deterioration and service life of RCBMs. The damage variables proposed in this paper can provide a reference point for this purpose.
6 Conclusions
In this paper, the static compression properties of NCM and RCM were analyzed by uniaxial compression and cyclic loading-unloading tests, and the effects of curing humidity and rubber aggregates on the matrix structure were discussed. Finally, based on the strain equivalence principle and statistical theories, the uniaxial compression damage constitutive model of RCM with different curing humidity was established, and the experimental and theoretical results were verified.
1) NCM and RCM undergo similar damage during uniaxial compression in dry- and wet-curing conditions and their stress-strain curves can be divided into four evolution stages: initial compaction, linear elastic, plastic, and post-peak failure stage. It is observed that the initial compaction stage (△εOA)

Figure 17 Damage variable-strain curves of specimens:
2) In dry- and wet-curing conditions, there is a positive correlation between the peak stress loss ratio and the rubber content, and there is a negative linear correlation between the peak strain and the rubber content. Also, the peak strain increases when the curing humidity decreases.
3) Under cyclic loading-unloading with variable loads, the variation trends of residual strain differences of the NCM and the RCM, at each cyclic level with the number of cycles are basically the same, and both factors develop with the trend of increasing at first, then decreasing, and re-increasing. Indeed, the failure modes of NCM and RCM are different.
4) The evolution trend of the stress-strain curves under the cyclic loading-unloading tests with variable loads can be described directly through the change of residual strain differences, and it can be explained that the specimens have irreversible plastic damage under the cyclic loading-unloading tests with variable loads. From the strain evolution process of the specimens under cyclic loading-loading test, it positively reflects the irreversible load damage of the specimen under uniaxial compression.
5) The results show that the established model can appropriately describe the full stress-strain relationship, and the damage variable of the constitutive model proposed in this paper accurately characterizes and predicts the evolution of mechanical damage in RCM under uniaxial compression.
Contributors
The overall research direction and goal were jointly put forward by YANG Rong-zhou, XU Ying, and CHEN Pei-yuan. The experiment was carried out jointly by YANG Rong-zhou and GONG Jiu. YANG Rong-zhou analysed the experimental data, put forward and established the idea and model to characterize the damage of the sample, and completed the writing of the manuscript. XU Ying and CHEN Pei-yuan revised and improved the manuscript constructively. All authors replied to reviewers’ comments and revised the final version.
Conflict of interest
YANG Rong-zhou, XU Ying, CHEN Pei-yuan, and GONG Jiu declare that they have no conflict of interest.
References
[1] Youssf O, ElGawady M A, Mills J E. Static cyclic behaviour of FRP-confined crumb rubber concrete columns [J]. Engineering Structures, 2016, 113: 371-387. DOI: 10.1016/j.engstruct.2016.01.033.
[2] LV Jing, ZHOU Tian-hua, DU Qiang, WU Han-heng. Effects of rubber particles on mechanical properties of lightweight aggregate concrete [J]. Construction and Building Materials, 2015, 91: 145-149. DOI: 10.1016/j.conbuildmat.2015.05.038.
[3] Rashad A M. A comprehensive overview about recycling rubber as fine aggregate replacement in traditional cementitious materials [J]. International Journal of Sustainable Built Environment, 2016, 5(1): 46-82. DOI: 10.1016/j.ijsbe.2015.11.003.
[4] Siddika A, Mamun M A A, Alyousef R, Amran Y H M, Aslani F, Alabduljabbar H. Properties and utilizations of waste tire rubber in concrete: A review [J]. Construction and Building Materials, 2019, 224: 711-731. DOI: 10.1016/j.conbuildmat.2019.07.108.
[5] Gonen T. Freezing-thawing and impact resistance of concretes containing waste crumb rubbers [J]. Construction and Building Materials, 2018, 177: 436-442. DOI: 10.1016/j.conbuildmat.2018.05.105.
[6] Strukar K, SipoS T K, MiliCeviC I, BuSiC R. Potential use of rubber as aggregate in structural reinforced concrete element—A review [J]. Engineering Structures, 2019, 188: 452-468. DOI: 10.1016/j.engstruct.2019.03.031.
[7] Xue J, Shinozuka M. Rubberized concrete: A green structural material with enhanced energy-dissipation capability [J]. Construction and Building Materials, 2013, 42: 196-204. DOI: 10.1016/j.conbuildmat.2013.01.005.
[8] YANG Fei, FENG Wan-hui, LIU Feng, JING Lin, YUAN Bing, CHEN De. Experimental and numerical study of rubber concrete slabs with steel reinforcement under close-in blast loading [J]. Construction and Building Materials, 2019, 198: 423-436. DOI: 10.1016/j.conbuildmat.2018.11.248.
[9] Aslani F, Ma G W, Wan D L Y, Muselin G. Development of high-performance self-compacting concrete using waste recycled concrete aggregates and rubber granules [J]. Journal of Cleaner Production, 2018, 182: 553-566. DOI: 10.1016/j.jclepro.2018.02.074.
[10] LIU Feng, MENG Liang-yu, NING Guo-fang, LI Li-juan. Fatigue performance of rubber-modified recycled aggregate concrete (RRAC) for pavement [J]. Construction and Building Materials, 2015, 95: 207-217. DOI: 10.1016/j.conbuildmat. 2015.07.042.
[11] Thomas B S, Gupta R C, Kalla P, Cseteneyi L. Strength, abrasion and permeation characteristics of cement concrete containing discarded rubber fine aggregates [J]. Construction and Building Materials, 2014, 59: 204-212. DOI: 10.1016/j.conbuildmat.2014.01.074.
[12] Turatsinze A, Garros M. On the modulus of elasticity and strain capacity of self-compacting concrete incorporating rubber aggregates [J]. Resources, Conservation and Recycling, 2008, 52(10): 1209-1215. DOI: 10.1016/ j.resconrec.2008. 06.012.
[13] ZHANG Hai-bo, GUAN Xue-mao, GOU Mi-feng, LIU Xiao-xing. Influence of rubber aggregate on pore structure of cement mortar [J]. Materials Reports, 2013, 27(7): 126-133. DOI: 10.3969/j.issn.1005-023X.2013.14.034. (in Chinese)
[14] ZHU Han, WANG Zhong-jian, XU Jie, HAN Qing-hua. Microporous structures and compressive strength of high-performance rubber concrete with internal curing agent [J]. Construction and Building Materials, 2019, 215: 128-134. DOI: 10.1016/j.conbuildmat.2019.04.184.
[15] GUO Qi, ZHANG Ru-yi, LUO Qi-rui, WU Han, SUN Hu-ping, YE Yi. Prediction on damage evolution of recycled crumb rubber concrete using quantitative cloud imagine correlation [J]. Construction and Building Materials, 2019, 209: 340-353. DOI: 10.1016/j.conbuildmat.2019.03.115.
[16] Aparicio S, Martinez-Ramirez S, Molero-Armenta M, Fuente J V, Hernandez M G. The effect of curing relative humidity on the microstructure of self-compacting concrete [J]. Construction and Building Materials, 2016, 104: 154-159. DOI: 10.1016/j.conbuildmat.2015. 12.057.
[17] MI Zheng-xiang, HU Yu, LI Qing-bin, AN Zai-zhan. Effect of curing humidity on the fracture properties of concrete [J]. Construction and Building Materials, 2018, 169: 403-413. DOI: 10.1016/j.conbuildmat.2018.03.025.
[18] Atis C D, Ozcan F, Kilic A, Karahan O, Bilim C, Severcan M H. Influence of dry and wet curing conditions on compressive strength of silica fume concrete [J]. Building and Environment, 2005, 40(12): 1678-1683. DOI: 10.1016/ j.buildenv.2004.12.005.
[19] LUO Da-ming NIU Di-tao. Influences of water-to-cement ratio and curing condition on water absorption of internal curing concrete [J]. Journal of Building Structures, 2019, 40(1): 165-173. DOI: 10.14006/j.jzjgxb.2019.01.019. (in Chinese)
[20] MI Zheng-xiang, HU Yu, LI Qing-bin, GAO Xiao-feng, YIN Tao. Maturity model for fracture properties of concrete considering coupling effect of curing temperature and humidity [J]. Construction and Building Materials, 2019, 196: 1-13. DOI: 10.1016/j.conbuildmat.2018.11.127.
[21] SHEN De-jian, WANG Ming-liang , CHEN Ying, WANG Tao, ZHANG Jin-Yang. Prediction model for relative humidity of early-age internally cured concrete with pre-wetted lightweight aggregates [J]. Construction and Building Materials, 2017, 144: 717-727. DOI: 10.1016/j.conbuildmat. 2017.03.088.
[22] LYU Zheng-hua, GUO Yin-chuan, CHEN Zhi-hui, SHEN Ai-qin, QIN Xiao, YANG Jing-yu, ZHAO Ming, WANG Zhen-long. Research on shrinkage development and fracture properties of internal curing pavement concrete based on humidity compensation [J]. Construction and Building Materials, 2019, 203: 417-431. DOI: 10.1016/j.conbuildmat. 2019.01.115.
[23] LI Li-juan, RUAN Sheng-hua, ZENG Lan. Mechanical properties and constitutive equations of concrete containing a low volume of tire rubber particles [J]. Construction and Building Materials, 2014, 70: 291-308. DOI: 10.1016/ j.conbuildmat.2014.07.105.
[24] WANG Su-sheng, XU Wei-ya, YANG Lan-lan. Experimental and elastoplastic model investigation on brittle-ductile transition and hydro-mechanical behaviors of cement mortar [J]. Construction and Building Materials, 2019, 224: 19-28. DOI: 10.1016/j.conbuildmat.2019.07.046.
[25] XU Ying, YANG Rong-zhou. Dynamic mechanics and damage evolution characteristics of rubber cement mortar under different curing humidity levels [J]. Journal of Materials in Civil Engineering, 2020, 32(10). DOI: 10.1061/(ASCE)MT. 1943-5533.0003351.
[26] YANG Rong-zhou, XU Ying, CHEN Pei-yuan, GE Jin-jin. Compressive rupture and energy evolution characteristics of rubber fine aggregate cement mortar under dry and wet curing conditions [J]. Materials Reports, 2020, 34(4): 4049-4055. DOI: 10.11896/cldb.18120117. (in Chinese)
[27] YANG Lin-hu, ZHU Han, ZHANG Ya-mei. Effect of crumb rubber on pore structure of cement mortar [J]. Journal of Tianjin University, 2011, 44(12): 1083-1087. (in Chinese)
[28] JGJ/T 70-2009. Standard for test method of basic properties of construction mortar [S]. (in Chinese)
[29] LI Dong, JIN Liu, DU Xiu-li, LIU Jing-bo. Determination of intergranular and transgranular failure of mesoscale model concrete under mode-I fracture [J]. Theoretical and Applied Fracture Mechanics, 2020, 107: 102551. DOI: 10.1016/ j.tafmec.2020.102551.
[30] Samouh H, Rozièere E, Loukili A. Experimental and numerical study of the relative humidity effect on drying shrinkage and cracking of self-consolidating concrete [J]. Cement and Concrete Research, 2019, 115: 519-529. DOI: 10.1016/j.cemconres.2018.08.008.
[31] LI Yang, ZHANG Xu, WANG Rui-jun, LEI Yan. Performance enhancement of rubberised concrete via surface modification of rubber: A review [J]. Construction and Building Materials, 2019, 227: 116691. DOI: 10.1016/j.conbuildmat.2019.116691.
[32] DING Qing-jun, LI Jin-hui, GENG Xue-fei, ZHAO Ming-yu. Mechanism of enhancing anti-abrasion performance of ultrahigh-performance concrete via rubber particles [J]. Journal of the Chinese Ceramic Society, 2020, 48(10): 1-8. DOI: 10.14062/j.issn.0454-5648.20200247. (in Chinese)
[33] Abdelmonem A, El-Feky M S, NasR E S A R, Kohail M. Performance of high strength concrete containing recycled rubber [J]. Construction and Building Materials, 2019, 227: 116660. DOI: 10.1016/j.conbuildmat. 2019.08.041.
[34] HOU Yun-fen. Cementitious material [M]. Beijing: China Electric Power Press, 2012. (in Chinese)
[35] LONG Guang-cheng, LIU He, MA Kun-lin, XIE You-jun. Uniaxial compression damage constitutive model of concrete subjected to freezing and thawing [J]. Journal of Central South University (Science and Technology), 2018, 49(8): 1884-1892. DOI: 10.11817/j.issn.1672-7207.2018.08.007. (in Chinese)
[36] Lemaitre J. How to use damage mechanics [J]. Nuclear Engineering and Design, 1984, 80(2): 233-245. DOI: 10.1016/0029-5493(84)90169-9.
[37] Lemaitre J. Local approach of fracture [J]. Engineering Fracture Mechanics, 1986, 25(5, 6): 523-537. DOI: 10.1016/0013-7944(86)90021-4.
[38] Arson C. Generalized stress variables in continuum damage mechanics [J]. Mechanics Research Communications, 2014, 60: 81-84. DOI: 10.1016/j.mechrescom.2014.06.006.
[39] Sakin R, AY I. Statistical analysis of bending fatigue life data using Weibull distribution in glass-fiber reinforced polyester composites [J]. Materials & Design, 2008, 29(6): 1170-1181. DOI: 10.1016/j.matdes.2007.05.005.
[40] Correia J, Apetre N, Arcari A, Jesus A D, Muniz-Calvente M, Calcada R, Berto F, Fernandez-Canteli A. Generalized probabilistic model allowing for various fatigue damage variables [J]. International Journal of Fatigue, 2017, 100(1): 187-194. DOI: 10.1016/j.ijfatigue. 2017.03.031.
[41] HAIDYRAH A S, NEWKIRK J W, CASTANO C H. Weibull statistical analysis of Krouse type bending fatigue of nuclear materials [J]. Journal of Nuclear Materials, 2016, 470: 244-250. DOI: 10.1016/j.jnucmat.2015.12.016.
[42] XU Ying, LI Cheng-jie, ZHENG Qiang-qiang, NI Xian, WANG Qian-qian. Analysis of energy evolution and damage characteristics of mudstone under cyclic loading and unloading [J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(10): 2084-2091. DOI: 10.13722/ j.cnki.jrme.2019.0153. (in Chinese)
[43] KURUMATANI M, TERADA K, KATO J, KYOYA T, KASHIYAMA K. An isotropic damage model based on fracture mechanics for concrete [J]. Engineering Fracture Mechanics, 2016, 155: 49-66. DOI: 10.1016/j.engfracmech. 2016.01.020.
[44] WANG Qian-feng. Study on dynamic damage characteristics of steel fiber reinforced concrete [D]. Yichang: Three Gorges University, 2009. DOI: 10.7666/d.d066359. (in Chinese)
(Edited by FANG Jing-hua)
中文导读
干、湿养护条件下橡胶水泥砂浆的静态压缩性能及损伤本构模型
摘要:为了研究橡胶水泥基材料(RCBMs)在干、湿养护条件下的静态压缩性能及力学损伤演化,对橡胶水泥砂浆(RCM)进行了单轴压缩和循环加-卸载试验。分析了在95% (湿润养护)和50% (干燥养护)相对湿度养护条件下单轴压缩试件和湿润养护下循环加-卸载试件的力学性能。结果表明,在单轴压缩试验中,试件在干燥养护下的峰值应力损失率高于湿润养护的。峰值应变随着橡胶含量的增加而减小,随着养护湿度的降低而增大。在循环加-卸载试验下,普通水泥砂浆(NCM)和RCM在各循环水平的残余应变差随循环次数的变化趋势基本相同,但两者的破坏模式不同。对试件基体内部细观结构的SEM观察表明,降低养护湿度和掺加橡胶骨料均进一步增大了水泥砂浆的初始损伤。采用基于应变等效原理和统计理论建立损伤本构模型来描述RCM的单轴压缩特征,有效表征和预测了力学损伤演化规律。
关键词:养护湿度;橡胶水泥砂浆;单轴压缩;循环加-卸载;细观损伤;本构模型
Foundation item: Projects(52008003, 52074009) supported by the National Natural Science Foundation of China; Project(201904a07020081) supported by the Key Research and Development Program Project of Anhui Province, China; Project(1908085QE213) supported by the Nature Science Foundation of Anhui Province, China
Received date: 2020-05-03; Accepted date: 2021-01-07
Corresponding author: XU Ying, PhD, Professor; Tel: +86-15956655885; E-mail: yxu@aust.edu.cn; ORCID: https://orcid.org/0000-0001-8438-3130

