面向多质量特征的产品质量损失成本模型及其应用

赵延明^{1, 2}，刘德顺³，张俊³，柳乔³

(1. 中南大学 机电工程学院，湖南 长沙，410083；

2. 湖南科技大学 信息与电气工程学院，湖南 湘潭，411201；

3. 湖南科技大学 机械设备健康维护省重点实验室，湖南 湘潭，411201)

摘要：针对产品多质量特征与零部件的尺寸之间不能直接利用几何原理得出显式关系表达式，很难建立产品级的质量损失模型的现状，提出一种基于神经网络法和层次分析法的质量损失模型。为了尽量减少主观随意性对权重确定的影响，采用神经网络法处理产品历史数据确定权重。考虑零件加工过程中的返修成本和报废成本，采用分段质量损失函数对田口质量损失函数进行改进，使其更加贴近工程实际，并根据零件尺寸服从不同的分布，导出相应的零件质量损失成本。研究结果表明：该质量损失模型为隐式关系建模提供了有效解决方法。

关键词：多质量特征；质量损失；神经网络法；层次分析法

中图分类号：TH124            文献标志码：A         文章编号：1672-7207(2012)05-1753-11

Quality loss cost model and its application to products with multi-quality characteristics

ZHAO Yan-ming^{1, 2}, LIU De-shun³, ZHANG Jun³, LIU Qiao³

(1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;

2. School of Information and Electrical Engineering, Hunan University of Science and Technology,

Xiangtan 411201, China;

3. Hunan Provincial Key Laboratory of Health Maintenance for Mechanical Equipment,

Hunan University of Science and Technology, Xiangtan 411201, China)

Abstract: Based on the fact that the explicit relation expression between product multi-quality characteristics and the dimensional tolerance of component is not educed directly with geometry principle and the product-level quality loss cost is difficult to establish, a quality loss cost model with neural network method and analytic hierarchy process (AHP) was processed. In order to decrease the impact of subjective randomness, the weights are determined with neural network method to product historical data process. Taking rework costs and scrap costs into account during the course of manufacturing mechanical parts, the piecewise quality loss function was used to improve Taguchi quality loss function, which is very close to engineering practice. The corresponding quality loss costs were deduced with the different distribution of part dimension. The results show that the quality loss cost model provides an effective method for the implicit relation model.

Key words: multi-quality characteristics; quality loss; neural network method; analytic hierarchy process

公差不仅影响产品的制造成本，而且影响产品质量。公差、制造成本、质量损失之间存在着非常密切的关系：若公差过小，则由质量特征的波动带来的质量损失就小，但制造成本高；若公差过大，则制造成本低，但质量损失大。为此，很多学者在公差优化设计方面进行了大量的研究工作，力求进行既能满足产品性能质量要求而制造成本又最低的最佳公差分配。Huang等^[1]以产品制造成本与质量损失最小为目标对多重相关关键公差进行同步设计，以轮的装配为实例，与框架、轮、轴、轴衬、螺母的设计参数之间的关系表达式为基础进行推导。Muthu等^[2]以质量损失成本与制造成本之和最小为目标函数对装配中各零件的公差进行优化，并采用遗传算法和粒子群优化算法对其进行求解。以单向离合器的装配为实例，其质量损失成本是以质量特征(接触角)与离合器的轮毂高度、滚子直径、外壳内径之间的关系表达式为基础进行推导。Ye等^[3]通过同时考虑工序公差和设计公差的分配使以质量损失和制造成本的组合为目标函数最小，以汽车的活塞与气缸的装配为例，以质量特征(装配间隙)与活塞外径、气缸内径的关系表达式为基础进行分析。彭和平等^[4]推导了多重相关特征产品的质量损失与有关零件工序公差的函数关系，建立了基于制造成本-质量损失的并行公差设计的优化综合模型。以圆锥齿轮的装配为实例，其质量损失成本是通过尺寸链得出多个质量特征(2个装配间隙)与各零件的尺寸之间的关系函数来推导的。上述研究成果都是以几何量(部件装配尺寸)为质量特征，再根据几何原理(尺寸链关系)直接得出质量特征与零件公差之间的关系，然后，建立部件级质量损失成本模型。而对以物理量为质量特征、质量特征与零件公差由几何原理不能直接建立关系的产品级的质量损失研究很少。产品质量认为是产品满足规定要求或潜在的需求特征和特性的总和^[5]，而田口提出产品质量就是产品上市后给社会造成的损失，但不包括产品功能本身产生的损失^[6]。产品对社会的损失越小，用户越满意，产品的质量就越好。通常，产品质量是由产品的１个或多个质量特征来体现的，用户主要关注的也是产品质量特征，而不是产品零部件的某个具体尺寸的公差或公差体系，并且不同顾客、不同时期对产品质量特征及其波动范围要求也不同。很多产品的质量特征是物理量，很难利用几何原理与产品零部件的公差建立关系模型，因此，也很难直接建立产品级的质量损失成本模型。用户对微型电动机的质量主要关注其多个质量特征如负载转速、负载电流、空载转速、空载电流等物理量，而不是电动机中某些具体的零部件的公差。利用几何原理无法将电动机这些质量特征与零部件的尺寸公差直接建立关系模型。在公差并行设计中，需要综合考虑产品制造成本和质量损失成本，而现已有很多成熟的零件制造成本模型^[7-9]，故质量损失成本的建模研究尤为重要。赵延明等^[10]采用应用层次分析法通过产品质量特征将零部件公差与产品质量损失联系起来，解决了定量描述零部件公差与产品质量损失之关系问题，但在确定判断矩阵的过程中存在专家评判的主观随意性。为了克服主观因素对质量损失模型的影响，并充分利用产品历史数据，本文作者提出一种基于神经网络法和层次分析法的产品质量损失成本模型。

1  质量损失成本建模

每个产品都有１个或多个质量特征，产品质量是由这些质量特征综合表征的。而产品又是由零部件装配而成的，因此，每个零部件的质量(公差)都会对产品的各个质量特征产生影响，也会影响整个产品的质量，其关系模型如图1所示。要求出产品质量损失，首先需推出各零件尺寸公差对每个特征的质量损失，然后推出各质量特征对产品的质量损失。

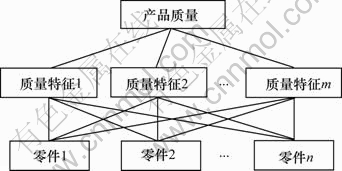
图1  关系模型

Fig.1  Relationship model

设产品具有m个质量特征、n个零件，可得出零件尺寸波动引起的产品质量的质量损失为：

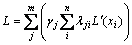           (1)

其中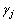：为第j个质量特征对产品质量损失的权重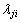；为第i个零件尺寸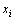波动对第j个质量特征的质量损失权重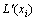；为第i个零件由尺寸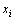的波动所造成的质量损失。

权重的确定方法分为主观和客观2类赋权法。主观赋权法是专家凭经验对各指标进行赋权的方法，如

层次分析法、专家调查法等，具有主观随意性；而客观赋权法是根据各指标已有数据按一定的规则或算法进行赋权的方法，如神经网络法、目标规划法等。在产品质量损失的表达式中，有2级权重需要确定：第1级是零件的质量损失到质量特征的质量损失，为了消除以往权重确定过程中人为影响及缺乏动态性的弊端，尽量减少主观因素对权重确定的影响^[11-12]，利用人工神经网络方法对产品零件加工尺寸数据和质量特征的实验数据进行处理，再利用神经网络的各层权系数进行相应的变换来确定该级的权重；第2级是质量特征的质量损失到产品的质量损失，由于产品质量的好坏主要是用户满不满意，而不能进行定量表达，因此，采用专家评判方法来确定各质量特征质量损失在产品质量损失中的重要性程度，然后，通过层次分析法来确定该级的权重。

1.1  神经网络法

神经网络是由大量的、简单的处理单元(神经元)广泛地互相连接而形成的复杂网络系统，它反映了人脑功能的许多基本特征，是一个高度复杂的非线性动力学系统。而BP神经网络是一种多层前馈型神经网络，1个3层BP网络，可以实现从输入到输出的任意非线性映射^[13]。

3层BP神经网络的拓扑结构如图2所示，包括输入层、隐含层、输出层。图2中：i为输入层神经元；j为隐含层神经元；k为输出层神经元；x_i为输入变量；x_j为隐含层输入变量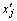；为隐含层输出变量；y_k为输出变量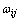；为x_i与x_j之间的权重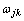；为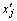与y_k之间的权重。BP算法的学习过程由前向传播和反向传播组成，在前向传播过程中，输入信息从输入层经隐含层逐层处理，并传向输出层。若在输出层不能得到期望值，则反向传播。前向传播的网络输出计算过程如下。

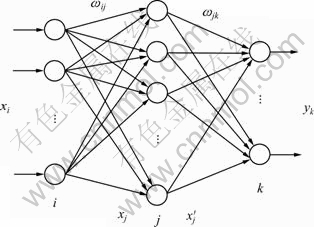
图2  BP神经网络的拓扑结构

Fig.2  Topology structure of BP neural network

(1) 隐含层神经元的输入为所有输入的加权之和，可得：

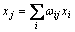              (2)

(2) 隐含层神经元的输出采用S传递函数激发，可得：

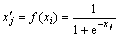           (3)

(3) 输出层输出采用线性传递函数激发，可得：

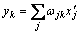              (4)

1个神经网络的输出结果与输入参数之间的映射关系完全由网络的各层间的权系数决定，用样本数据训练好神经网络，那么其各层间的权系数就被确定。若把产品各零件的相关加工尺寸作为神经网络的输入、产品各质量特征作为神经网络的输出，根据产品已有历史数据训练好网络，然后，对该网络的权系数进行适当处理就可得到各零件的质量损失权重。下面对处理方法进行研究。在此把网络各层输入变量对输出变量的影响作用的相对程度定义为贡献率(R_c)。

(1) 设隐含层输出变量为单位向量，即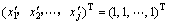，则根据(4)式可得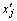对y_k的贡献率：

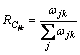                (5)

(2) 设输入层输入变量为单位向量，即(x₁, x₂, …, x_j)^T =(1, 1, …, 1)^T，则根据式(2)和(3)可得x_i对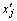的贡   献率：

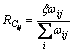                 (6)

其中：系数。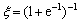

(3) 输入变量x_i对输出变量y_k的贡献率为：

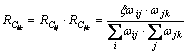         (7)

(4) 通过对神经网络的各层权系数进行处理后，得到的贡献率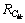并非都为正，故需对其进行变换到[0,1]。孙会君等^[11-12]在由神经网络各层权系数到权重的确定过程中采用取绝对值的方式来处理负权系数，存在不妥之处。于洋等^[14]在无纲量化处理中采用指数函数进行变换有局限性，不能得到[0,1]的整个区间。为了使变换后的数据能真正反映原数据的规律和特性，并保持较高的转换精度，得到[0,1]的整个区间，采用式(8)进行变换：

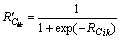                      (8)

 (5) 对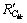进行归一化处理，得出神经网络的每个输入对输出的贡献率：

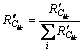              (9)

由于神经网络的输入是产品各零件的相关加工尺寸，神经网络的输出是产品各质量特征，故各零件的质量损失权重为。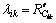

1.2  层次分析法

层次分析法(AHP)是由Satty提出的，其是将复杂问题分解成多个组成因素，并把这些因素按支配关系形成递阶层次结构。通过两两比较的方式确定层次中各因素的相对重要性，然后，综合决策者的判断，确定决策方案相对重要性的总排序。整个过程体现了系统工程学定量与定性分析相结合的思想，并利用一定的标度把人的主观判断进行客观量化^[15]。

1.2.1  判断矩阵确定

层次分析法主要是建立系统的递阶层次结构后，按上一层次中某一准则对同一层次的各元素进行两两比较其重要性，并按比例标度重要性程度1~9构造比较判断矩阵，矩阵表达式为：

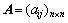              (10)

其中：a_ij元素i与元素j相对于上一层次中某一准则重要性的比例标度。

1.2.2  权重确定

根据n个元素对于每一准则的判断矩阵A，确定它们对于该准则的相对权重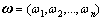，计算权重的方法主要有和法、根法、特征根方法、最小二乘法、对数最小二乘法等。前２种方以使用于精度要求不高的情况，特征根法在AHP中有特别重要的理论意义及实用价值而得到广泛应用。因此，在此使用该方法进行权重计算：

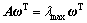             (11)

其中：λ_max为判断矩阵A的最大特征根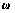；为相应的特征向量。

对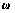经下式进行归一化后就可以作为权重向量：

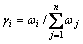             (12)

1.2.3  一致性检验

通常，在AHP中采用比较法检验判断矩阵A的一致性，若判断矩阵A是一致性的，则λ_max=n，其中n为判断矩阵A的阶数。一般定义I_C作为一致性指标。

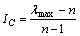              (13)

由于阶数越高，判断矩阵A很难达到一致性，故萨迪提出了用平均随机一致性指标I_R修正I_C的方   法^[14]。在AHP中被普遍采用，把R_C作为一致性检验的指标：

R_C=I_C/I_R               (14)

当R_C＜0.1时，判断矩阵具有可接受的一致性，否则判断矩阵偏离一致性程度过大，而需要进行调整，以便使判断趋于一致，得到较合乎逻辑的排序。

1.3  分段质量损失模型

田口提出了质量损失函数的概念，认为产品的质量特征值偏离目标值，就会造成损失^[6]。根据用户对质量特征值的期望，提出3种质量损失函数。

(1) 望目特性的质量损失函数：

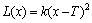             (15)

其中：x为产品质量特征值；T为质量特征值的目标值；k为质量损失系数。

(2) 望小特性的质量损失函数：

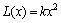               (16)

(3) 望大特性的质量损失函数：

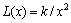             (17)

由于田口质量损失函数是简单的平方型损失函数，存在着无界性、连续性、对称性，这些都与实际不太相符。针对田口质量损失函数的局限性，国内外学者对质量损失函数进行了改进。李跃波等^[16]根据质量损失函数必须满足的条件，提出了逆正态型质量损失函数，解决了田口质量损失函数的无界性。孙棣华等^[17]采用逆正态型的质量损失函数，建立了一般情形下多维质量属性的质量损失函数模型。张根保等^[18]结合质量损失发生的实际情况，采用分段函数理论对田口质量损失函数进行了拓展，建立了质量损失的分段模型。王伯平等^[19]应用分段函数理论对田口损失模型进行扩展，建立了更符合工程实际的分段曲线质量损失模型，但没有计入零件返修成本和报废成本对质量损失的影响。

在制造过程中，根据质量特征值偏离目标值的程度，零件产品可以分为合格品、返修品、废品，因此，零件的质量损失区域也可以分为合格区(质量特征值在技术要求规定的范围之内)、返修区(经过返修可使质量特征值回到技术要求规定的范围之内)、废品区(无法使质量特征值回到技术要求规定的范围之内)。由于这３个区域中的质量损失成本不同，因此，在田口质量损失函数的基础上，根据零件加工尺寸在不同情况下可返修。本文采用更符合工程实际的分段质量损失函数，根据零件服从实际的分布，导出其质量损失成本。

1.3.1  望目特性质量损失函数

零件的加工尺寸超出技术要求的公差范围[L_SL, U_SL]，就认为不合格品；若通过返修使加工尺寸在   [L_SL, U_SL]之内，则产品仍然为合格品，只是增加了一定的返修成本，反之则只能报废。因此，望目特性质量损失函数可分为2种形式：一种是零件加工尺寸小于L_SL可返修的形式，另一种是零件加工尺寸大于U_SL可返修的形式。

(1) 零件加工尺寸小于L_SL可返修的情况。若零件加工尺寸x(如孔类零件的孔径尺寸)小于L_SL，则零件就不合格，但通过返修可使零件合格。因此，把质量损失函数分成4段，如图3所示，其表达式如式(18)所示。

质量损失函数为：

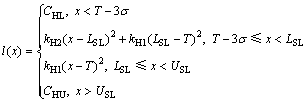   (18)

其中：C_HL为返修最大成本；质量损失系数为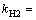 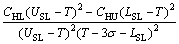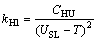；；C_HU为报废成本；σ为尺寸x的方差。

假设零件加工尺寸x服从正态分布，概率密度函数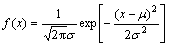(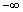＜x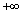＜)，其质量损失成本为：

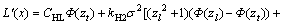
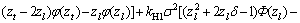
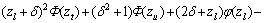
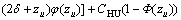        (19)

其中：；；；；，。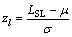

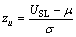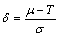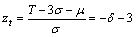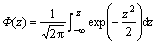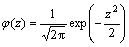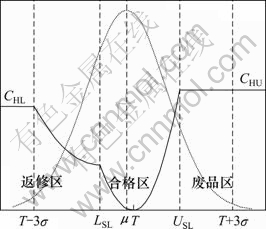
图3  望目特性质量损失函数Ⅰ

Fig.3  Quality loss function Ⅰof the-nominal-the-best

(2) 零件加工尺寸超过U_SL值可返修的情况。若零件加工尺寸x(如轴类零件的外圆直径尺寸)大于U_SL，零件就不合格，但通过返修可使零件合格。因此，把质量损失函数分成4段，如图4所示，其表达式为：

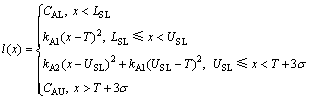  (20)

其中：C _AL为报废成本；质量损失系数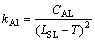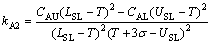，；C_AU为返修最大成本；σ为尺寸x的方差。

假设零件加工尺寸x服从正态分布，概率密度函数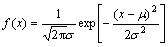(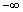＜x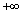＜)，其质量损失成本为：

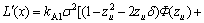
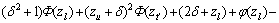
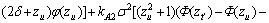
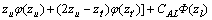    (21)

其中：。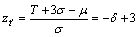

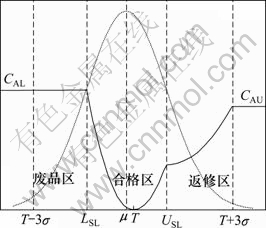
图4  质量损失函数Ⅱ

Fig.4  Quality loss functionⅡof the-nominal-the-best

1.3.2  望小特性质量损失函数

零件的加工尺寸越小越好，超出技术要求U_SL，就认为不合格品；若通过返修使质量特征值小于U_SL，则产品仍然为合格品，只是增加了一定的返修成本；反之则只能报废。因此，把质量损失函数分成4段，如图5所示，其表达式如式(22)所示。质量损失函数：

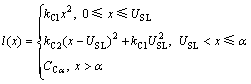  (22)

其中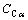：为报废成本；质量损失系数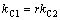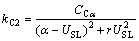，；损失系数比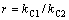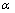；为置信度。

当1个随机二维向量的2个分量呈独立的、服从正态分布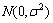时，该向量的模服从瑞利分布。若零件的加工尺寸x是形位公差同轴度，则其服从瑞利分布^[20-22]。瑞利分布的概率密度函数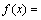

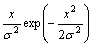 (x≥0)，其期望值为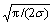，方差

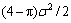为。根据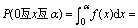99.73%，可得出置信度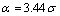，其质量损失成本为：

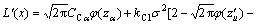
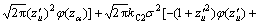
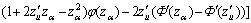  (23)

其中：；；。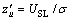

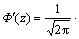
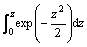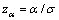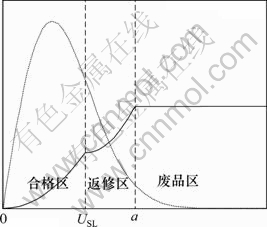
图5  望小特性质量损失函数

Fig.5  Quality loss function of the-smaller-the-better

2  应用实例

2.1  关系模型确定

微型电动机产品质量主要由输出轴上的转矩和转速所决定，而转矩与电枢电流成比例关系，由此确定负载转速、负载电流、空载转速、空载电流这4个质量特征来综合表征微型电动机产品质量。

微型电机的结构形式有多种多样，但其主要由静止的定子部分和转动的转子部分构成，并且定子与转子之间有一定间隙。定子部分主要包括机壳、主磁极、电刷装置等，转子部分主要包括铁芯、转子绕组、换向器等。1对磁极的直流电机的磁场分布示意图如图6所示，由N极(永磁体)发出来的磁通，大部分经过气隙进入电枢齿，经过电枢磁轭(铁芯)到另一部分的电枢齿，通过气隙进入S极，再经过定子磁轭(机壳)回到原来出发的N极，构成闭合的磁路。由于机壳、铁芯、永磁体的磁阻远小于气隙的磁阻，故可近似认为磁通势都降在2个气隙上，气隙是否均匀对称直接影响着磁通势的分布，从而影响直流电机的产品质量。从微型电动机结构可知影响气隙和对称性的零件有机壳、永磁体、转子铁芯、轴、轴承、轴承座，因此，从这些零件的加工尺寸中选取影响气隙的因素为铁芯直径、转轴直径、机壳内径、永磁体固定后内径、前轴承座同心度、后轴承座同心度、换向器直径、径器          。

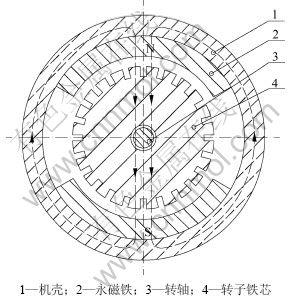
图6  微型电动机结构剖面示意图

Fig.6  Structure section of micro-motor

根据上面对微型电动机表征产品质量的质量特征以及影响因素，可以得出微型电动机产品质量、质量特征、零件之间的关系模型，如图7所示。

2.2  权重计算

在微型电动机的关系模型中，可知有2级权重需要确定。为了消除人为影响，第1级权重采用BP神经网络法确定，第2级权重采用层次分析法来确定。

2.2.1  第1级权重计算

记录影响微型电动机磁场气隙因素的检验结果，并给每个零件编号，然后，按编号装配190台微型电动机，在相同实验环境下测出每台微型电动机各质量特征值，这样，得到190组实验数据作为BP神经网络的训练样本。该型号微型电动机影响因素的设计尺寸和公差、加工尺寸的均值和方差，如表1所示、径器 。将各影响因素的尺寸参数(铁芯直径(x₁)、转轴直径(x₂)、机壳内径(x₃)、永磁体固定后内径(x₄)、前轴承座同心度(x₅)、后轴承座同心度(x₆)、换向器直径(x₇))作为BP神经网络的输入，把各质量特征值(负载转速、负载电流、空载转速、空载电流)分别作为BP神经网络的输出，建立7—28—1型BP网络模型，隐含层神经元的传递函数采用logsig，输出层神经元传递函数采用purelin，训练函数采用trainbfg。

为了消除输入、输出原变量量纲不同以及数值差异太大带来的影响，提高神经网络的训练精度，采用如下方法对其进行归一化处理：

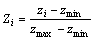             (24)

式中：z_i为原变量；z_max为原变量的最大值；z_min为原变量的最小值；Z_i为归一化后的变量，。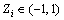

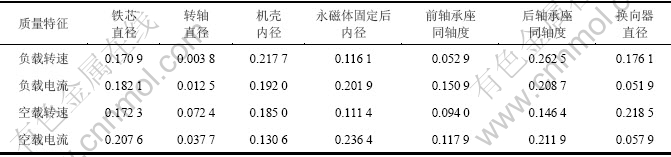
采用170组数据进行网络训练得到网络的权系数，再根据上述质量损失权重确定方法得到各影响因素对各质量特征的质量损失权重，如表2所示。

采用20组数据作为网络模型验证，质量特征的实测值与网络预测值进行相关性分析，实测值与预测值之间的拟合关系，如图8所示。负载转速、负载电流、空载转速、空载电流的相关系数分别为97.9%，96.7%，99.6%和99.9%。所有相关系数都大于95.0%，故该网络模型精确，说明第1级权重是精确的。

2.2.2　第2级权重计算

采用专家评判法对影响微型电动机产品质量的各质量特征的重要程度进行确定：负载转速比空载转速稍重要，负载电流的重要性介于负载转速和空载转速之间，空载转速比空载电流稍重要。按1~9比例标度重要性程度赋值构造比较判断矩阵为：

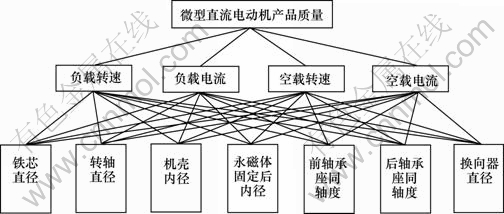
图7  微型电动机的关系模型

Fig.7  Relationship model of micro-motor

表1  零件尺寸

Table 1  Parts dimension

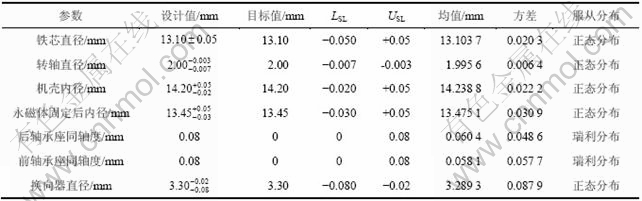
表2  第1级权重λ_ji

Table 2  First-stage weights

根据式(11)可以求出λ_max=4.019 2和λ_max对应的特征向量ω=[4.019 2  2.358 1  1.323 6  0.492 5]，由式 (12)归一化得到负载转速、负载电流、空载转速、空载电流对产品质量损失的权重分别为0.490 5，0.287 8，0.161 5和0.060 1。由式(13)和(14)进行一致性检验，检验指标R_C=0.007 1＜0.100 0，故判断矩阵A具有可接受的一致性。

2.2.3  权重分析

通过神经网络法和层次分析法计算出微型电动机关系模型中的两级权重矩阵，分别表示产品影响因素尺寸(零件相关尺寸)对质量特征的质量损失权重和质量特征对产品的质量损失权重，把这2个权重矩阵相乘，得到铁芯直径、转轴直径、机壳内径、永磁体固定后内径、前轴承座同轴度、后轴承座同轴度、换向器直径对产品质量损失的权重分别为0.176 5，0.019 4，0.199 8，0.147 3，0.091 6，0.225 2和0.140 1。后轴承座同轴度、机壳内径、铁芯直径对产品质量损失权重较大，分别占22.53%，19.98%和17.65%。因此，对这些影响因素的质量应进行严格控制。而转轴直径对产品质量损失权重较小，只占1.94%，因此，可采用较宽松的质量控制。

2.3  产品质量损失成本计算与分析

在微型电动机的影响因素中，机壳内径、永磁体固定后内径尺寸的加工属于零件加工尺寸小于L_SL可返修的情况，并服从正态分布，采用式(19)计算质量损失成本；铁芯直径、转轴直径、换向器直径的加工属于零件加工尺寸大于U_SL可返修的情况，并服从正态分布，采用式(21)计算质量损失成本；后轴承座同轴度、前轴承座同轴度是属于望小特性质量损失情况，并服从瑞利分布，采用式(23)计算质量损失成本。并结合所确定的权重，由式(1)得出微型电动机质量损失成本。

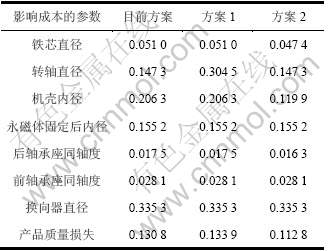
根据目前该型号的微型电动机各影响因素的设计参数和实验统计数据(如表1所示)、返修成本、报废成本以及损失系数比(如表3和表4所示)，可得出各影响因素的质量损失以及产品的质量损失，如表5  所示。

根据以上计算，可以进行定量分析零部件级的公差对产品级质量损失的影响。各零部件在调整设计参数后的加工尺寸是采用Monte Carlo原理通过计算机仿真产生，再算出各影响尺寸的统计数据(均值和方差)。

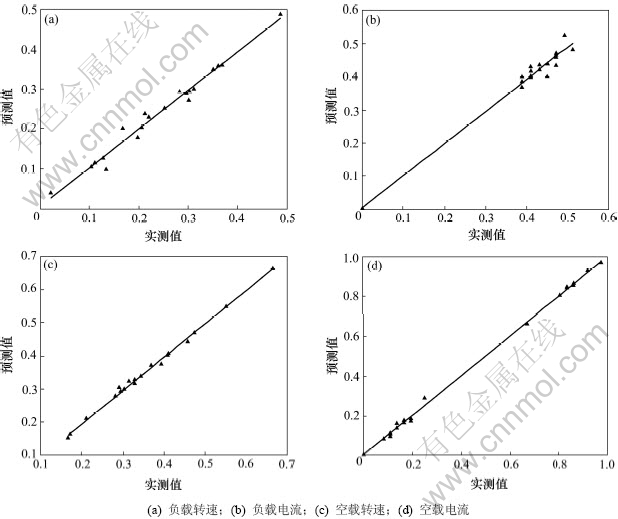
图8  质量特征实测值与预测值拟合关系

Fig.8  Fitted relation between measured value and predicted value of quality characteristics

 (1) 放宽转轴直径公差控制，取其设计参数为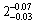 mm，其他影响因素不变，均值为1.948 9 mm，方差为0.011 7。其公差带增大了10倍，经计算可得由转轴直径引起的质量损失增加134.2%，但微型电动机的质量损失仅增加2.4%。

(2) 对后轴承座同轴度、机壳内径、铁芯直径进行较严格控制，取后轴承座同轴度的设计参数为0.04，铁芯直径的设计参数为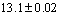 mm、机壳内径的设计参数为 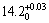mm，其他影响因素不变；后轴承座同轴度的均值为0.030 2 mm，方差为0.025 1；铁芯直径的均值为13.101 5 mm，方差为0.007 8；机壳内径的均值为14.21 5 mm，方差为0.008 7。计算结果如表5所示。从表5可看出：由于提高后轴承座同轴度、机壳内径、铁芯直径的加工精度而引起微型电动机的质量损失只减少13.8%。可见：提高产品各零件的加工精度并不是减少产品级的质量损失的唯一途径。适当增大对产品质量损失影响小的零件的公差，虽然会增大该零件本身的质量损失，但对产品总体质量损失影响并不大，同时，还可以减少产品的制造成本。

表3  返修和报废成本

        Table 3  Rework costs and scrap costs       元

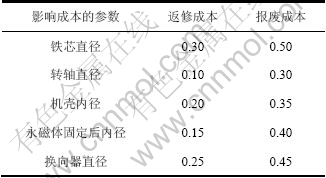
表4  报废成本与损失系数比

Table 4  Scrap costs and loss coefficient ratio

表5  质量损失成本

             Table 5  Quality loss cost            元

3  结论

(1) 提出了一种基于神经网络法和层次分析法的产品级质量损失模型，采用神经网络方法处理产品历史数据并确定其权重，减少了主观随机性对权重确定的影响。

(2) 考虑零部件加工的返修成本和报废成本，对田口质量损失函数进行了改进，使其更加贴近工程  实际。

(3) 采用质量损失模型可对产品多质量特征和零部件的尺寸公差直接建立关系模型，该质量损失模型提供了有效解决方法，并为公差并行优化设计提供了条件。

参考文献：

[1] HUANG Mei-fa. Concurrent process tolerance design based on minimum product manufacturing cost and quality loss[J]. Int J Adv Manuf Technol, 2005, 25: 714-722.

[2] Muthu P V, Sankaranarayanasamy D K. Optimal tolerance design of assembly for minimum quality loss and manufacturing cost using metaheuristic algorithms[J]. Int J Adv Manuf Technol, 2009, 44: 1154-1164.

[3] Ye B, Salustri F A. Simultaneous tolerance synthesis for manufacturing and quality[J]. Research in Engineering Design, 2003, 14: 98-106.

[4] 彭和平, 刘晓军, 蒋向前. 基于多重相关特征质量损失函数的并行公差设计[J]. 中国机械工程, 2010, 21(6): 690-697.
PENG He-ping, LIU Xiao-jun, JIANG Xiang-qian. Concurrent tolerance design based on quality loss function with multi- correlated characteristics[J]. China Mechanical Engineering, 2010, 21(6): 690-697.

[5] 吴昭同, 余忠华, 陈文华. 保质设计[M]. 北京: 机械工业出版社, 2004: 20-23.
WU Shao-tong, YU Zhong-hua, CHEN Wen-hua. Guaranteed quality design[M]. Beijing: China Machine Press, 2004: 20-23.

[6] Taguchi G, Elsayed E A, Hsiang T C. Quality engineering in production system[M]. New York: McGraw-Hill, 1989.

[7] Chase K W, Parkinson A R. A survey of research in the application of tolerance analysis to the design of mechanical assemblies[J]. Research in Engineering Design, 1991, 3: 23-37.

[8] DONG Z. New production cost-tolerance models for tolerance synthesis[J]. ASME Journal of Engineering for Industry, 1994, 116(5): 199-206.

[9] 杨将新, 吴昭同. 机械加工成本-公差建模技术的研究[J]. 浙江大学学报: 自然科学版, 1996, 30(5): 517-522.
YANG Jiang-xin, WU Zao-tong. A study on modelling techniques for product cost-tolerance[J]. Journal of Zhejiang University: Natural Science, 1996, 30(5): 517-522.

[10] 赵延明, 刘德顺, 徐小艳, 等. 面向零件公差设计的产品质量损失成本模型[J]. 中国机械工程, 2011, 22(11): 1347-1351.
ZHAO Yan-ming, LIU De-shun, XU Xiao-yan, et al. A novel quality loss cost model for product tolerance design[J]. China Mechanical Engineering, 2011, 22(11): 1347-1351.

[11] 孙会君, 王新华. 应用人工神经网络确定评价指标的权重[J]. 山东科技大学学报: 自然科学版, 2001, 20(3): 84-86.
SUN Hui-jun, WANG Xin-hua. Determination of the weight of evaluation indexes with artificial neural network method[J]. Journal of Shandong University of Science and Technology: Natural Science, 2001, 20(3): 84-86.

[12] 刘贵, 于伟东. 毛精纺前纺工艺参数重要性的BP网络定量评价法[J]. 纺织学报, 2008, 29(1): 34-37.
LIU Gui, YU Wei-dong. Quantitative evaluation method for the significance of worsted fore-spinning parameters based on BP neural network[J]. Journal of Textile Research, 2008, 29(1): 34-37.

[13] 董长虹. Matlab神经网络与应用[M]. 北京: 国防工业出版社, 2007: 64-100.
DONG Chang-hong. Matlab neural network and application[M]. Beijing: National Defense Industry Press, 2007: 64-100.

[14] 于洋, 李一军. 基于多策略评价的绩效指标权重确定方法研究[J]. 系统工程理论与实践, 2003(8): 8-15.
YU Yang, LI Yi-jun. Research on giving weight for performance indicator based on the multi-strategy method[J]. Systems Engineering-theory & Practice, 2003(8): 8-15.

[15] 王莲芬, 许树柏. 层次分析法引论[M]. 北京: 中国人民大学出版社, 1990: 5-18.
WANG Lian-fen, XU Shu-bo. Introduction of analytic hierarchy process[M]. Beijing: China Renmin University Press, 1990: 5-18.

[16] 李跃波, 周树民. 一种新的损失函数[J]. 武汉工业大学学报, 1999, 21(4): 86-87.
LI Yue-bo, ZHOU Shu-min. A sort of new loss function[J]. Journal of Wuhan University of Technology, 1999, 21(4): 86-87.

[17] 孙棣华, 刘飞, 但斌. 扩展质量损失函数模型的研究[J]. 机械工程学报, 1998, 34(2): 26-32.
SUN Di-hua, LIU Fei, DAN Bin. Study on extensive quality loss function modle[J]. Chinese Journal of Mechanical Engineering, 1998, 34(2): 26-32.

[18] 张根保, 刘帅帅, 张鹏, 等. 质量损失拓展模型及其经济性分析[J]. 中国机械工程, 2009, 20(17): 2094-2099.
ZHANG Gen-bao, LIU Shuai-shuai, ZHANG Peng, et al. Economic analysis on the extensive quality loss mode[J]. China Mechanical Engineering, 2009, 20(17): 2094-2099.

[19] 王伯平, 张会, 景大英. 分段曲线质量损失模型的研究[J]. 农业机械学报, 2007, 38(2): 150-152.
WANG Bo-ping, ZHANG Hui, JING Da-ying. Study on section curve quality loss function model[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(2): 150-152.

[20] 吴永宽, 于连璋. 零件与工装的形位精度理论与应用[M]. 北京: 机械工业出版社, 1994: 110-114.
WU Yong-kuan, YU Lian-zhang. The theory and application of Geometric accuracy of parts and process equipments[M]. Beijing: China Machine Press, 1994: 110-114.

[21] 刘明霞, 张宇, 杨慕升. 基于瑞利分布的形位误差统计过程控制比较研究[J]. 山东理工大学学报: 自然科学版, 2008, 22(2): 53-56.
LIU Ming-xia, ZHANG Yu, YANG Mu-sheng. Comparative study of statistical process control to geometrical error based on rayleigh distribution[J]. Journal of Shandong University of Technology: Natural Science Edition, 2008, 22(2): 53-56.

[22] 倪骁骅, 邓善熙. 形状误差的分布类型及评定模型[J]. 兰州理工大学学报, 2007, 33(6): 36-39.
NI Xiao-hua, DENG Shan-xi. Distribution type of form error and its evaluation model[J]. Journal of Lanzhou University of Technology, 2007, 33(6): 36-39.

(编辑 陈灿华)

收稿日期：2011-06-10；修回日期：2011-08-25

基金项目：国家自然科学基金资助项目(51075143)

通信作者：赵延明(1973-)，男，湖南湘潭人，博士研究生，讲师，从事公差优化、数据挖掘、工业控制与自动化研究；电话：13107123527；E-mail: hnust_zhao@yahoo.com.cn