DOI: 10.11817/j.issn.1672-7207.2017.05.025

基于CFD-DPM耦合法新型差压密度计中水泥浆液流动特性分析

李静雅，徐力生，徐蒙

(中南大学 地球科学与信息物理学院，有色金属成矿预测与地质环境监测教育部重点实验室，

湖南省有色金属资源与地质灾害探查重点实验室，湖南 长沙，410083)

摘要：为了揭示水泥浆液密度检测过程中运动规律，基于欧拉-拉格朗日法建立连续-离散相模型，通过CFD连续模型和DPM离散模型分别求解液相速度分布和固相颗粒运动轨迹，对差压密度计中水泥浆液流速场和颗粒场进行模拟。研究结果表明：在差压密度计测量过程中，水灰比为5:1~3:1的低质量分数浆液沿测量筒中心线和横截面方向均匀分布，水灰比为3:1~0.5:1的高质量分数浆液沿测量筒中心线方向均匀分布，沿横截面方向呈一阶递减梯度分布，常规质量分数水泥浆液在核心测量区域内基本呈稳定流动状态；水灰比为0.5:1~5:1的浆液固相颗粒均匀分布于测量筒内，未出现局部聚集和真空区域。双耦合模型解决了水泥浆液传统模型模拟失真问题，为差压密度计研发过程中水泥浆液流动状态的分析提供了依据。

关键词：CFD-DPM；水泥浆液；流动特性；水灰比；固液两相流

中图分类号：TP212；TV543         文献标志码：A         文章编号：1672-7207(2017)05-1308-08

Flow characteristic analysis of grout in new type differential pressure densimeter based on CFD-DPM coupling method

LI Jingya, XU Lisheng, XU Meng

(Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring of

Ministry of Education, Key Laboratory of Non-ferrous Resources and Geological Hazard Detection,

School of Geosciences and Info-Physics, Central South University, Changsha 410083, China)

Abstract: To reveal the velocity and particle distribution regularity in the measuring cylinder, a coupling method of continuous and discrete phase model was established based on Euler-Lagrange method. The velocity distribution was solved by the CFD continuous model and the solid-phase particle trajectory was solved by DPM discrete model, and the velocity and particle field in the new type differential pressure densimeter were simulated. The results show that, during the measurement of the new type densimeter, the flow velocity of low concentration grouts with water-cement ratio of 5:1-3:1 has a uniform distribution along the center line and transverse direction of the cylinder, while high concentration grouts with water-cement ratio of 3:1-0.5:1 has a uniform distribution along the center line but gradient distribution along the transverse direction of the cylinder, and so normal concentration grouts show laminar flowing state in the core measuring area of the cylinder. Solid particle is distributed evenly over the cylinder and there is no special local accumulation or vacuum area for grouts with water–cement ratio of 0.5:1-5:1. Double coupling model solves the simulate distortion of tradition single model and provides specific evidence for the development of new type differential pressure densimeter.

Key words: CFD-DPM; cement grout; flow characteristic; water-cement ratio; solid liquid two phase flow

对于固液两相流的模拟和计算，传统方法有2种：一是将液相和固体颗粒相视为一种混合物，采用伪单相流体模型进行流场计算，也就是混合理论；二是将颗粒相视为拟流体，采用双流体模型进行流场计算。这2种方法都取得了一定成果。20世纪80年代，采用测量仪器测到的参量只有固液混合值，无法测到固液两相各自的特征值，将固相颗粒和液相流体的混合物看作一种新的流体为研究带来一定方便。国外较早提出该理论，BOWEN^[1-2]通过混合模型(mixture theory)建立了可压缩多孔介质模型，对可压缩和不可压缩液体进行了研究，得出体积分数和化学组成分别决定可压缩和不可压缩混合物的孔隙压力。倪晋仁等^[3]在混合理论基础上对泥沙流速度分布和质量分数分布进行了研究，指出研究流速分布应考虑建立浑水流速分布与悬沙质量分数分布的关系，并在具体应用时采用分段法，浑水流速分布模式便于对非均质流、均质两相流及清水水流进行统一处理。随着测量仪器的发展，出现了基于欧拉-欧拉法的双流体模型(two fluid model)，将流体相和离散相都看作连续介质且均在欧拉参考系下进行研究。吴玉林等^[4]为提高离心泵抗磨蚀能力，在多相紊流双流体模型的基础上建立了两相紊流运动大涡模拟模型，对离心泵叶轮内部的固液两相流动进行模拟，计算得出液相压力分布和相对速度场及固相颗粒分布。双流体模型的离散相和连续相具有相同的控制方程，计算量小，效率高，是当时多相体系CFD模拟的主要方法^[5-6]。上述研究中液相和固相均按照连续介质理论进行求解, 在实际应用中存在一定的局限性。当颗粒相质量分数较低时，固液两相流运动主要由液相作用控制，可选用单一CFD连续模型近似描述；当颗粒相质量分数较高时，固液两相流运动主要由离散相颗粒控制，离散结构特性显著，若继续使用连续模型，则会偏离流体实际情况。为解决上述问题，研究者将液相置于欧拉坐标系下求解、固相置于拉格朗日坐标系下求解，建立了连续-离散相耦合模型，并逐渐成为研究固液两相流的主导方法^[7-9]。WU等^[10]通过CFD-DPM模型解决了流化床流动过程中质量守恒以及因颗粒聚合造成质量分数不均产生误差问题。吴春笃等^[11]采用DPM模型对旋流分离器中的低质量分数固液两相流进行模拟，获得分离器内部三维速度分布云图，在分离效率简单易算并为后期设计的完善提供有效依据。ROZA等^[12]使用连续-离散相双向耦合模型计算模拟了沉淀池中颗粒流动轨迹, 并分析比较了不同颗粒直径和体积分数流体的流动特性，确定了影响油罐效率的关键因素。因此，CFD-DPM双模型耦合法更贴近流体运动过程中的受力情况，在实际应用中可以较真实地模拟流体运动状态。本文作者基于欧拉-拉格朗日法建立CFD-DPM连续-离散相模型，充分考虑液相的连续介质特性和固体颗粒相的离散特性及相间相互作用，在离散相对连续相有影响的流场中求解颗粒分布，通过两相间交替迭代计算，描述固液两相流中颗粒的运动情况及其与流场间的能量交换，为差压密度计的研发过程中水泥浆液流动状态提供明确的判定依据。

1  差压密度计方法及原理

差压法测密度源于静压液位测量原理，适用于静止或低速层流流动液体。本文流体介质为流动水泥浆液，会产生一定误差。只有满足特定条件即水泥浆液低速稳定流过测量筒，压力传感器测得的压力才有效，求解的密度才有效。测量筒中浆液的理想流动状态为层流，因此，本次模拟的目的是验证水泥浆液在测量筒中的流动状态及颗粒分布情况。差压密度计建立于独立稳定的自循环测量系统，电机运转带动泵工作，将水泥浆液从进浆口泵送至测量筒，充满测量筒并从顶部缓缓溢出，经出浆口流回浆桶，结构如图1所示。压力传感器是测量核心元件，测量筒顶至压力传感器中心线距离H为450 mm，即被测液体高度是固定值，不同密度的浆液在压力传感器位置产生的压力不相同且线性相关，根据主机记录的压力由压强公式求解被测浆液密度。

图1  测量筒结构

Fig. 1  Structure of measuring system

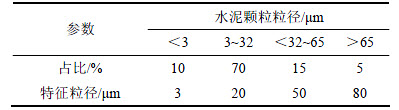
常用水泥浆液水灰比为0.5:1~5:1，水泥浆液水灰比(密度)不同意味着固体颗粒质量分数不同，流体也相应地呈现不同特性^[13-14]。当固体颗粒质量分数＜10%即水灰比＞3时，浆液整体呈现液相特性，可采用双流体模型进行研究；当固体颗粒质量分数＞10%即水灰比＜3时，固体颗粒间的离散特性显著，宏观连续介质理论不足以描述复杂的相间作用和颗粒运动，需选取连续-离散相模型进行研究^[15]。本文所研究的水泥浆液水灰比有90%小于3，因此，本文统一使用两相耦合法进行求解。实际的水泥浆液固相颗粒粒径不是单一的，而是接近正态分布。近年来，随着ISO标准的实施和新型干法水泥技术的快速发展，我国大型水泥的粒径分布发生了巨大变化，龙世宗等^[16]对全国大范围的水泥粒径分布进行检测，得到普通硅酸盐水泥主要粒径分布范围。模拟两相流时，需将颗粒的全部粒度分成若干粒度组合，每个粒度组合由1个特征粒径表示，颗粒的轨迹将依据此特征粒径进行计算。依据前面的水泥粒径普查结果和模拟要求，划分水泥浆液颗粒粒度，如表1所示。

表1  水泥浆液颗粒尺寸

Table 1  Particle size of cement grout

2  两相控制方程及耦合

2.1  基本控制方程

2.1.1  连续相控制方程

1) 质量守恒方程为

          (1)

2) 动量守恒方程为

        (2)

式中：α为连续流体相的体积率，%；ρ为流体相密度，kg/m³；p为静压，Pa；v_i为流体相在笛卡尔坐标i方向上的流速分量，m/s；g_i为坐标i方向上的体积力，N；τ_ij为黏性应力张量，N/m；F_i为连续相与离散相的相互作用力，N。

2.1.2  离散相运动方程

通过求解拉格朗日坐标系下的颗粒作用力微分方程，得到离散相颗粒的运动轨迹。颗粒作用力平衡方程在笛卡尔坐标系下的形式(x方向)为：

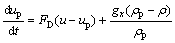        (3)

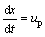                 (4)

式中：u为连续相在x方向的速度，m/s；为连续相在x方向的密度，kg/m³；u_p为离散相颗粒在x方向的速度，m/s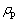；为离散相颗粒在x方向的密度，kg/m³；F_D为颗粒的单位质量阻力，N。颗粒的单位质量阻力F_D表达式为

               (5)

式中：C_D为阻力系数；μ为连续相动力黏度，Pa·s；d_p为离散相颗粒粒径，mm；Re为雷诺数。

阻力系数C_D可采用下式计算：

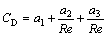              (6)

固相颗粒假设为球形，在一定雷诺数范围内，系数a₁，a₂和a₃可近似为常数。结合本文实际情况，流体雷诺数＜2 300，系数取值均为1。

2.2  两相耦合

欧拉-拉格朗日两相耦合模型是在离散相和连续相相互作用的流场中考察颗粒的分布。离散相影响连续相流场，连续相流场影响离散相的分布，通过交替计算连续相和离散相直到两相的计算结果满足收敛要求为止。在软件耦合计算中，需要进行时间步长匹配。步长匹配要求FLUENT的时间步长能够保证流体计算的迭代收敛，不能小于离散相的时间步长且为离散相的整数倍。时间步长指剪力波穿过1个固相颗粒所需的时间。

           (7)

式中：R为颗粒半径，mm；ρ为颗粒密度，kg/m³；G为颗粒剪切模量，Pa；ν为泊松比。计算时一般可选取的10%~15%作为时间步长进行计算。

在1个时间步长内，先假定计算域中不存在离散相，在FLUENT中进行流场计算，求解雷诺平均N-S方程直到迭代收敛；然后在计算域中引入离散相，求解颗粒运动方程得到颗粒运动轨迹和体积率；更新连续相的颗粒源项，重新给颗粒定位；将数据反馈回FLUENT中，开始下一个时间步迭代，直到获得耦合收敛解为止。整体耦合流程如图2所示。

图2  CFD-DPM耦合流程图

Fig. 2  Flow chart of CFD-DPM coupling

3  模拟计算与分析

3.1  计算域网格划分

依据图1(b)所示测量筒结构图，应用CATIA三维设计软件对测量筒建模，具体参数如下：测量筒直径为100 mm，高度为700 mm(进口中心线至测量筒顶)；进口段直径为40 mm，长度为100 mm；围挡直径为200 mm，高度为100 mm；出口段直径为70 mm，长度为300 mm，呈11°角倾斜。建模完成后，将测量筒整体计算域的模型文件导入ICEM软件进行计算网格划分，由于进口段与测量筒尺寸差异较大，需要分区域网格划分。本文将测量筒划分为进口段、测量段和出口段3个区域相邻界面采用分界面连接，从计算时间考虑，采用混合网格；进口段和测量段计算域结构相对简单，采用结构网格；出口段为异形结构，采用适应性较好的非结构网格。总网格数为571 288，网格质量由网格柱状数据图表示，数值范围为0~1，值越大，表示网格质量越高。本文模拟区域网格划分及网格质量如图3所示。

3.2  计算前处理设置

将生成的网格文件导入Fluent软件的前处理模块进行计算的前处理设置，该步骤是模拟计算的核心部分。前处理主要包括计算模型的选择、边界条件及介质参数、收敛标准等设置。本次模拟目的是验证测量筒内水泥浆液稳态流动，因此，计算模型选择层流模型；模拟工况设定如下：额定功率为1.1 kW和转速为1 450 r/min。在此工况下，计算模拟各质量分数浆液在测量桶内流速及颗粒轨迹，分析不同质量分数浆液从进口开始到顶部出口流动状态的稳定性。按照水泥浆液水灰比的不同分为5个工况，各工况边界条件如表2所示。在求解迭代过程中，对数值解的收敛性进行监控，设置残差标准为10^-4数量级；壁面区域采用无滑移固壁条件，壁面粗糙度R_a=0.4 μm(依据实际加工情况和ISO粗糙度对照表选取)。

图3  计算域网格划分

Fig. 3  Mesh division of calculation region

表2  各工况水泥浆液边界条件

Table 2  Boundary conditions under different working conditions

3.3  计算结果及分析

通过上述求解过程得到各节点的数值解后，运用FLUENT软件后处理器将整个计算域上的结果表示出来。本文选取速度云图和颗粒轨迹图输出模拟结果，并由此判断水泥浆液在测量筒中的流动状态。

3.3.1  收敛性

软件默认当所有变量的残差都降到低于10^-3时，判断计算收敛。本文设定的残差标准为10^-4，选取5:1，1:1，0.5:1共3个代表性水灰比浆液进行迭代计算，残差收敛结果如图4所示。

图4  迭代计算收敛曲线

Fig. 4  Convergence curves of iterative computation

由图4可知：3种工况质量守恒残差虽未达到设定收敛标准，但已达到软件默认残差标准且随着步数增加残差趋于稳定，可以判定收敛；对于5:1的低质量分数浆液，计算至80步时，达到软件默认收敛标准，Z方向速度分量达到设定的残差标准，判定收敛；对于1:1的中等质量分数浆液，计算至将近120步时，达到设定的残差标准，判定收敛；对于0.5:1的高质量分数浆液，计算至将近160步时，达到软件默认残差标准，Z方向速度分量达到设定的残差标准判定收敛；同时，随着浆液质量分数增加，需计算较多步数才能达到收敛标准。综上所述，本次模拟计算收敛性良好，模拟结果在一定程度上可以反映水泥浆液在测量筒中的流动状态，具有实际指导意义。

3.3.2  各工况速度场

由前面测量原理及模拟目的分析可知，水泥浆液在测量筒中流动状态是影响新型密度计测量精度的关键因素，因此，速度分布云图是本次模拟的重点。各工况下测量筒内速度分布如图5所示，不同颜色代表每种工况下测量桶内不同区域相对速度。

在浆液密度测量过程中，压力传感器嵌入筒壁一定深度(10 mm)，测量筒半径为50 mm，因此，测量的核心区域为测量筒内半径为40 mm的环形区域。由图5可知被测浆液流过测量筒时速度呈现如下分布规律：在测量筒两侧近壁面区域，浆液在流动过程中受到黏滞阻力作用，出现狭窄低速带，该区域为非核心测量区域，对测量结果影响可忽略；对于低质量分数浆液，流速核心测量区域出现1个均匀高速带，带内浆液流动速度相等；对于高质量分数浆液，核心测量区域出现2个高速带，其中，一个是测量筒中心区域狭窄高速带，另一个是次高速测量带且该区域内浆液流动速度相等。

3.3.3  颗粒相运动轨迹

除了速度分布云图外，颗粒运动轨迹图也是分析浆液流动状态的辅助指标。当浆液流动为层流状态时，由于流速稳定、流线平行，颗粒在运动过程中分布较均匀；当浆液为紊流状态时，受到流速大小和反方向变化的影响，颗粒在流动中会出现局部堆积，造成测量元件的堵塞或局部磨损。在模拟过程中，对颗粒进行编码，不同颜色代表不同颗粒，跟踪每个颗粒的运动轨迹，结果如图6所示。

由图6可知：对于水灰比为5:1至0.5:1的工程常规质量分数浆液，水泥颗粒基本均匀分布于测量筒内，未出现颗粒局部聚集和真空区域，这在一定程度上说明浆液在流动过程中速度和方向相对稳定。水泥浆液颗粒粒径范围跨度较大，在模拟过程中选择特征粒径进行模拟，具体粒径及占比无法定量分析，该项模拟结果对水泥浆液流态分析提供辅助作用。

图5  4种典型工况速度云图

Fig. 5  Velocity nephograms under four typical conditions

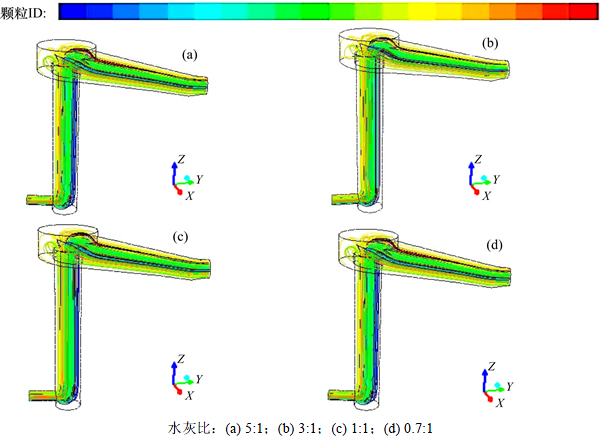
图6  各工况颗粒轨迹

Fig. 6  Particle tracks under four typical conditions

4  试验结果与仿真结果对比分析

配制5种常规质量分数的水泥浆液进行室内试验，在测量筒入口接入流量计用以计算测量筒内浆液的实际流速和流体雷诺数。雷诺数是1个判别黏性流体流动状态的量纲一参数Re(Re＜2 300，为层流)。

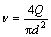                (8)

式中：v为浆液流速，m/s；Q为浆液流量，m³/s；d为测量筒直径，mm。

               (9)

式中：μ为浆液黏度，Pa·s；ρ为浆液密度，kg/m³；v为浆液流速，m/s；d为测量筒直径，mm。将压力传感器接入记录仪主机，传感器每3秒记录并传输1个数据，记录数据频率为100个/5 min。浆液黏度可由室内试验测定，平均流速可由流量计数据计算，且在模拟速度场时计算模拟平均流速，与模拟结果进行对比分析，结果如表3和图7所示。

表3  测量筒内主要参数及流态分析

Table 3  Main parameters and flow state analysis in measuring cylinder

图7  各水灰比浆液流速

Fig. 7  Flow velocities under different water-cement ratios

由表3 可知：测量筒内各水灰比浆液均在低速层流流动；除水灰比5:1的稀浆外，浆液模拟平均流速均低于实际平均流速，但两者差值较小。由图7可知：除了水灰比为0.5:1的超浓浆液，浆液流速基本稳定，与模拟结果基本一致，水灰比为5:1的低质量分数浆液流速稳定，与测量核心区域一个稳定流速带的模拟结果一致；水灰比为0.7:1~0.5:1的高质量分数浆液存在一定波动且随着浆液质量分数增加，试验结果和模拟结果吻合度有所下降，与核心区域2个稳定流速带结果一致。在整个试验过程中，水泥浆液在测量筒顶部呈溢流状态且所有设备元件运行良好，未出现堵塞及故障等情况，说明在测量过程中浆液均匀充满测量筒且流动顺畅，与颗粒轨迹模拟结果一致。总之，模拟结果与试验结果吻合度高，CFD-DPM连续-离散相耦合模型适用于水泥浆液，可较真实地模拟密度测量中浆液的流动特性，为新型差压密度计的研究提供明确的理论指导。

5  结论

1) 灌浆工程90%的常规质量分数浆液(水灰比为0.5:1~5:1)，颗粒质量分数大于10%(水灰比小于3)，属于密相流，固相颗粒离散特性显著，需选取CFD-DPM连续-离散相耦合模型求解流场。

2) 测量筒内存在中心高速分布带、次高速分布带和壁面区域低速带3种速度分布，对于水灰比为5:1~3:1的低质量分数浆液，存在1个高速分布带且带内浆液流动速度相等，核心测量区为层流流态；对于水灰比为3:1~0.5:1的高质量分数浆液，存在1个狭窄中心高速分布带和1个次高速分布带且测量带内浆液流动速度相等，核心测量区为层流流态；对于0.5:1~5:1全工况浆液，颗粒均匀分布于测量筒内。

3) CFD-DPM模型充分考虑固相液相间的相互作用，真实反映流体运动过程中的流动状态，但该模型忽略固相颗粒之间的内部作用力，因此，在后期研究中，将水泥颗粒间的作用力计入相间作用力并对模型加以修正，使得对流体流动特性的模拟更加准确。

参考文献：

[1] BOWEN R M. Incompressible porous media models by use of the theory of mixtures[J]. International Journal of Engineering Science, 1980, 18(9): 1129-1148.

[2] BOWEN R M. Compressible porous media models by use of the theory of mixtures[J]. International Journal of Engineering Science, 1982, 20(6): 697-735.

[3] 倪晋仁, 惠遇甲. 浑水流速分布与悬移质质量分数分布的关系[J]. 泥沙研究, 1988(2): 18-28.

NI Jinren, HUI Yujia. The relation between the velocity distribution and the suspended concentration distribution[J]. Journal of Sediment Research, 1988(2): 18-28.

[4] 吴玉林, 葛亮, 陈乃祥. 离心泵叶轮内部固液两相流动的大涡模拟[J]. 清华大学学报(自然科学版), 2001, 41(10): 90-96.

WU Yulin, GE Liang, CHEN Naixiang. Large eddy simulation of silt-liquid two-phase flow through a centrifugal pump impeller[J]. Journal of Tsinghua University (Natural Science), 2001, 41(10): 90-96.

[5] 李良超, 徐斌, 杨军. 基于计算流体力学模拟的下沉与上浮颗粒在搅拌槽内的固液悬浮特性[J]. 机械工程学报, 2014, 50(12): 185-190.

LI Liangchao, XU bin, YANG Jun. Sinking/floating particles solid suspension characteristics in stirred tank based on CFD simulation[J]. Journal of Mechanical Engineering, 2014, 50(12): 185-190.

[6] 石战胜, 洪坤, 王维. 双流体模型的细网格模拟[J]. 计算机与应用化学, 2013, 30(9): 959-962.

SHI Zhansheng, HONG Kun, WANG Wei. Fine-grid simulation of fluidized beds using two-fluid model[J]. Computers and Applied Chemistry, 2013, 30(9): 959-962.

[7] WANG Shuyan, JIN Sun, QIAN Yang, et al. Numerical simulation of flow behavior of particles in an inverse liquid–solid fluidized bed[J]. Powder Technology, 2014, 261: 14-21.

[8] CHEN Xiaole, ZHONG Wenqi, SUN Baobin, et al. Study on gas/solid flow in an obstructed pulmonary airway with transient flow based on CFD-DPM approach[J]. Powder Technology, 2012, 217: 252-260.

[9] 安建彬, 张超, 陶婷. 基于耦合Lagrangian-Eulerian算法的流体机械数值模拟[J]. 山西建筑, 2016, 42(19): 211-212.

AN Jianbin, ZHANG Chao, TAO Ting. On fluid mechanic numeric simulation based on coupling Lagrangian-Eulerian calculation method[J]. Shanxi Architecture, 2016, 42(19): 211-212.

[10] WU C L, NANDAKUMAR K, BERROUK A S, et al. Enforcing mass conservation in DPM-CFD models of dense particulate flows[J]. Chemical Engineering Journal, 2011, 174(1): 475-481.

[11] 吴春笃, 张伟, 黄勇强, 等. 新型旋流分离器固液两相流的数值模拟[J]. 农业工程学报, 2006, 22(2): 98-102.

WU Chundu, ZHANG Wei, HUANG Yongqiang, et al. Numerical simulation of solid–liquid flow in a new kind of cyclone[J]. Transactions of the Chinese Society of Agricultural Engineering, 2006, 22(2): 98-102.

[12] ROZA T, ASTERIOS P. CFD methodology for sedimentation tanks: the effect of secondary phase using DPM coupled calculations[J]. Applied Mathematical Modeling, 2013, 37(5): 3478-3494.

[13] 倪晋仁, 曲铁众. 固液两相流中固体颗粒的垂直分选模型[J]. 水动力学研究与进展, 2003, 18(3): 349-354.

NI Jinren, QU Tiezhong. Modeling of vertical segregation of solid particles in sediment–laden flow[J]. Journal of Hydrodynamics, 2003, 18(3): 349-354.

[14] 阮文军. 基于浆液黏度时变性的岩体裂隙注浆扩散模型[J]. 岩石力学与工程学报, 2015, 24(15): 2709-2714.

RUAN Wenjun. Spreading model of grouting in rock mass fissures based on time-dependent behavior of viscosity of cement-based grouts[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 24(15): 2709-2714.

[15] 倪晋仁, 王光谦. 高质量分数恒定固液两相流运动机理探析(Ⅰ理论)[J]. 水利学报, 2000(5): 22-26.

NI Jinren, WANG Guangqian. Mechanism of hyper-concentrated flow (ⅠTheory)[J]. Journal of Hydraulic Engineering, 2000(5): 22-26.

[16] 龙世宗, 刘延生, 张福根. 我国大型水泥企业水泥粒径分布检测与分析[J]. 水泥, 2010(10): 20-23.

LONG Shizong, LIU Yansheng, ZHANG Fugen. Detection and Analysis of cement particle size distribution in Chinese large cement enterprise[J]. Cement, 2010(10): 20-23.

(编辑  陈灿华)

收稿日期：2016-11-02；修回日期：2017-01-19

基金项目(Foundation item)：国家自然科学基金资助项目(51208514)；国家中小企业创新基金资助项目(12C26214304879)；中南大学中央高校基本科研业务费专项资金资助项目(2011QNZT007) (Project(51208514) supported by the National Natural Science Foundation of China; Project(12C26214304879) supported by the National Small and Medium Enterprises Technology Innovation Foundation; Project(2011QNZT007) supported by the Scientific Research Special Foundation of Central South University)

通信作者：徐蒙，博士，副教授，从事灌浆工程仪器仪表研究；E-mail: 583100180@qq.com