
Kinetic Monte Carlo simulation of growth of
BaTiO3 thin film via pulsed laser deposition
ZHENG Xue-jun(郑学军)1, 2, YANG Bo(杨 博)1,
ZHU Zhe(朱 哲)1, WU Bo(吴 波)1, MAO Yu-liang(毛宇亮)1
1. Faculty of Materials and Photoelectronic Physics, Xiangtan University, Xiangtan 411105, China;
2. Key Laboratory for Low Dimensional Materials and Application Technology (Ministry of Education),
Xiangtan University, Xiangtan 411105, China
Received 15 July 2007; accepted 10 September 2007
Abstract: Considering the characteristics of perovskite structure, a kinetic Monte Carlo(KMC) model, in which Born-Mayer- Huggins(BMH) potential was introduced to calculate the interatomic interactions and the bonding ratio was defined to reflect the crystallinity, was developed to simulate the growth of BaTiO3 thin film via pulsed laser deposition(PLD). Not only the atoms deposition and adatoms diffusion, but also the bonding of adatoms were considered distinguishing with the traditional algorithm. The effects of substrate temperature, laser pulse repetition rate and incident kinetic energy on BaTiO3 thin film growth were investigated at submonolayer regime. The results show that the island density decreases and the bonding ratio increases with the increase of substrate temperature from 700 to 850 K. With the laser pulse repetition rate increasing, the island density decreases while the bonding ratio increases. With the incident kinetic energy increasing, the island density decreases except 6.2 eV<Ek<9.6 eV, and the bonding ratio increases at Ek<9.6 eV. The simulation results were discussed compared with the previous experimental results.
Key words: kinetic Monte Carlo simulation; pulsed laser deposition; BaTiO3 thin film; perovskite structure
1 Introduction
Barium titanate(BaTiO3) thin film is a typical ferroelectric thin film with perovskite structure, and has high dielectric constants and electro-optic coefficients[1]. Among various growth techniques, pulsed laser deposition(PLD) is a conventional growth technique used for growing complex muticomponent thin films[2], and it could improve layer-by-layer growth[3]. Although a few experiments reported on PLD growth of BaTiO3 thin film were focused on the influence of various parameters to the quality of thin films[1,4], and the initial stage in PLD growth of thin film has seldom been studied theoretically. Kinetic Monte Carlo(KMC) method could provide atomic-scale point of views on the growth of thin films, and was frequently used to simulate the growth of metal thin films and semiconducting thin films[5-6]. However, few simulations were performed on the perovskite ferroelectric thin films due to the complexity of the lattice structure and growth mechanism. Recently, XIAO et al[7] have performed KMC simulations on the growth of perovskite ferroelectric Pb(Zr, Ti)O3 (PZT) thin films. They have developed a KMC algorithm on the basis of perovskite structure to simulate the growth of PbTiO3(PT) thin film, and also simulated laser MBE growth of SrTiO3 thin film based on the three-dimensional solid-on-solid model. However, the above models are not suitable to simulate the growth techniques with high deposition rate such as PLD and magnetron sputtering.
In this work, based on the traditional energy-dependent KMC models, we developed the KMC algorithm to consider not only the deposition of atoms and the surface diffusion of adatoms but also the bonding of adatoms, in which the adatoms are bonded according to perovskite structure of BaTiO3 thin film. BMH potential was chosen to consider the interactions between the adatoms due to the short range interactions in the complicated perovskite structure, and the bonding ratio was defined to reflect the crystallinity that is an important property of crystalline BaTiO3 thin film. The effects of substrate temperature, laser pulse repetition rate and incident kinetic energy on growth of BaTiO3 thin film at submonolayer regime were studied in order to provide theoretical guideline for materials designs of ferroelectric thin film with perovskite structure.
2 Kinetic Monte Carlo model
2.1 Construction of perovskite structure
To construct the perovskite structure shown as Fig.1(a), there respectively are O, Ti, and Ba atoms in the face center, bulk center, and apex of the molecular cells. Accordingly, the square lattice substrate is of L×L sites, and the length of 0.2 nm per site is given in Fig.1(b). Each site can hold an atom and the periodic boundary condition is considered.
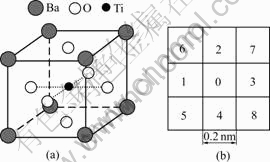
Fig.1 BaTiO3 perovskite structure (a) and square lattice substrate (b)
2.2 KMC algorithm
In the KMC model, there are three typical kinds of events during the submonolayer growth of BaTiO3 thin film, namely, deposition of atoms, surface diffusion of adatoms and bonding of adatoms. The two formers are kinetic processes with the specific rates, while the latter is non-kinetic. A list is constructed for all kinetic events that may occur in the process, and then one of the events is randomly selected with the probability proportional to its rate. After executing the selected event, the related local configurations and rates are changed, and the list should be updated accordingly. The time increment is determined by the inverse of the overall rate ?t=
 , where vi is the rate of event i to occur. During
, where vi is the rate of event i to occur. During
the submonolayer growth, the adatoms with the exhausted kinetic energies are permitted to bond with the neighbor adatoms, and it is called the bonding of adatoms.
2.2.1 Deposition of atoms
In PLD, the target material is ablated by a pulsed laser, and then deposited in regular pulses on the substrate surface. Experimentally, the laser pulsed lasts for a few nanoseconds, and the interval between two pulses is of the order of seconds. However, the pulse of evaporated atoms flux lasts for a few microseconds due to their speed distribution[8]. The atoms are deposited at randomly chosen positions on the substrate surface at an instantaneous flux Fi, while no atom reaches the substrate surface during the interval between two pulses. The average flux of incident atoms is Faver=tp×f×Fi, with t and f representing the pulse duration of incident flux and laser pulse repetition rate, respectively. The evaporated atom beam is regarded as a mixture of Ba, Ti and O atoms with the stoichiometric ratio of BaTiO3, Ba?Ti?O=1?1?3, and the atom deposited at a moment is randomly selected according to the ratio of atoms. The incident kinetic energies are simplified as uniform for all of the deposited atoms, and the deposition of an atom on the top of another adatom is invalid.
2.2.2 Surface diffusion of adatoms
Adatoms can hop to the first-nearest-neighbor sites before nucleation or being captured by islands. The hopping rate of an adatom for a specific move is determined by[9]
v=v0exp[-(EB-Ek)/kBT] (1)
where v0 is the attempt frequency (assumed to be 1.0×1012 Hz[10]), kB is the Boltzmann’s constant, T is the substrate temperature, and Ek is the adatom kinetic energy. If Ek≥EB, the hopping rate is generally assumed equal to the attempt frequency v0. The adatom kinetic energy will decrease after a hopping to
(Ek>EB)
(Ek≤EB)
 (2)
(2)
Additionally, EB is the energy barrier for specific move, which can be given by
EB=ED+ES (3)
where ES and ED are the interaction energy between the adatom and substrate and the energy difference between the present and hopping sites. Eij represents the interaction energy between the adatom at site (i, j) and all of the neighboring adatoms around it. If an adatom migrates from site (i, j) to (i′, j′), ED is given by
 (4)
(4)
where  with
with 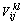 representing the
representing the
interaction energy between the adatoms at sites (i, j) and (k, l), and m representing the number of occupied neighbor sites. Only the first-nearest-neighbor and second-nearest-neighbor sites are taken into account in the interaction energy calculation. Being analogous to previous simulations on metal thin films[11], the long-range Coulombic interactions can be ignored by adopting the assumption that the incident atoms are neutral. On the other hand, BMH pair potential is more suitable to describe the interatomic interactions in the complicated perovskite structure[12]. Therefore, 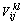 is given by the short-range interaction term of BMH pair potential[13]
is given by the short-range interaction term of BMH pair potential[13]
Vij(r)=Aijexp(-Bijr)-Cij/r6-Dij/r8 (5)
where r is the distance between atoms, Aij, Bij, Cij and Dij are BMH potential parameters. The BMH potential is effectively used in molecular dynamics simulations, for example, the simulation results of LaGaO3 bulk materials with perovskite structure are in good agreement with the experimental observations[12,14].
2.2.3 Bonding of adatoms
As shown in Fig.1(b), for site 0, sites 1 to 4 are the first-nearest neighbor sites, and sites 5 to 8 are the second-nearest-neighbor sites. According to the perovskite structure, Ba adatom can bond with its second-nearest-neighbor O adatoms, while Ti adatom can bond with its first-nearest- neighbor O adatoms. The bonded adatoms can not move any more, because Ba—O and Ti—O bonds are difficult to be broken. The adatom bonding process is performed after the kinetic energy exhausting of adatom, therefore it is considered a non-kinetic process. The bonding ratio Rb is defined by the ratio of bonded atom to incident atom Rb=nb/n, where nb represents the number of bonded atoms. A crystallization in the initial stage includes nucleation and coalescence, and the nucleation means the bonding of atoms. Therefore, the bonding ratio should be associated with the crystallinity of thin film. The larger the bonding ratio, the better the crystallinity.
2.3 Preparation of parameters
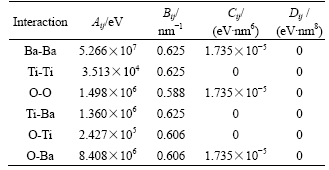
The simulation is performed on a square lattice substrate (L=100). The average flux of incident atoms Faver and pulse duration tp are fixed at 0.1 mL/s and 1.0×10-5 s[8]. The coverage is determined by θ=n/L2 with n representing the number of incident atoms, and the maximum coverage is 0.3. We adopt the interaction energy between the adatom and substrate as ES=1.2 eV [9], BMH potential parameters of BaTiO3 are taken from Materials Explorer software of Fujitsu Limited, as listed in Table 1. The island density N is defined by the average number of island per site N=ni/L2, where ni is the number of islands on substrate surface. High density of small islands may result in smoother thin film[8,15], which indicates that the island density at initial stage of growth will affect the surface roughness of thin film. In order to understand the influences of experimental parameters on PLD growth, the island density and bonding ratio of adatoms of the thin film at submonolayer regime were investigated under the different substrate temperature T, laser pulse repetition rate f and incident kinetic energy Ek.
Table 1 BMH potential parameters of BaTiO3
3 Results and discussion
3.1 Effect of substrate temperature
Fig.2 shows the island density and bonding ratio of adatoms as functions of the coverage(θ) at the different substrate temperatures at f=1 Hz and Ek=0 eV. From Fig.2(a), the island density at T=850 K is smaller than that at T=600, 700 and 800 K at higher coverage from 0.2 to 0.3. The ratio defined as R=D/Fi is a measure of the diffusion ability of all adatoms on substrate, where D=v0exp[-ES/(kT)] and Fi are the monomer diffusion rate and the incident flux. Obviously, with the substrate temperature, R increases and the island density decreases. Generally, the island density is primarily dominated by the ratio, and the larger the R, the smaller the island density [11]. This is why the island density at T=850 K is smaller than that at T=600, 700 and 800 K (see Fig.2(a)). During a pulse, the incident flux Faver equals the instantaneous flux Fi, and the value of R determined by D and Fi is smaller than 0.23 at T<700 K. In this case, the small value of R indicates that adatoms rarely diffuse in the pulse, so the island density is only determined by the deposition process that is not affected by the substrate temperature. This is the reason for the overlapping of island density curves at 600 and 700 K (see Fig.2(a)). This indicates that the temperature T can hardly influence the growth of BaTiO3 thin film, when it is lower than 700 K. It is close to the minimum substrate temperature 773 K for the activation of surface diffusion in PLD growth of BaTiO3 thin film[16]. As shown in Fig.2(b), the bonding ratio increases with the increase of coverage and substrate temperature from 700 to 850 K. According to Eqn.(1), a higher substrate temperature can enhance the mobility of atoms and increase the opportunities of bonding, therefore the larger bonding ratio corresponding to higher substrate temperature may improve the crystallinity of BaTiO3 thin film. It is in agreement with the experimental results of PZT and PT thin films deposited by PLD with perovskite structure [17-18]. Because the number of free sites decreases with the increase of coverage, the adatoms have more chances to bond with each other and the bonding ratio increases with the coverage.
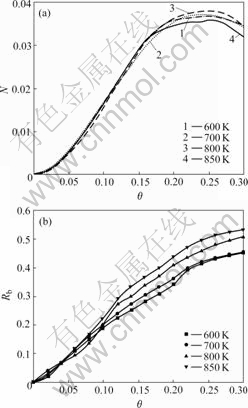
Fig.2 Island density (a) and bonding ratio (b) vs coverage at different substrate temperatures
3.2 Effect of laser pulse repetition rate
The effect of laser pulse repetition rate on surface morphology of BaTiO3 thin films was investigated at T=700 K and Ek=0 eV, and the surface morphologies at the laser pulse repetition rates 1 Hz and 100 Hz are given in Fig.3. Comparing Fig.3(a) with Fig.3(b), there are the lower island density and larger island size on the latter for the higher pulse repetition rate 100 Hz. The inset in Fig.3(b) shows the connection of atoms: Ti adatoms are connected with first-nearest-neighbor O adatoms, while Ba adatoms are connected with second-nearest- neighbor O adatoms.

Fig.3 Surface morphologies of BaTiO3 thin films at 1 Hz (a) and 100 Hz (b)
Fig.4 shows the island density and bonding ratio of adatoms as function of the coverage at the different laser pulse repetition rates at T=700 K and Ek=0 eV. From Fig.4(a), the island density decreases with the increase of repetition rate at the higher coverage from 0.2 to 0.3, and it is consistent with Hinnemann’s KMC simulation[19]. The instantaneous incident flux decreases with the increase of repetition rate because of the fixed Faver and tp, therefore the increase of repetition rate leads to the decrease of the nucleation possibility. On the other hand, the number of monomer decreases because of the monomers captured by islands during the pulse-off periods, therefore the nucleation possibility decreases when the next pulse comes. This implies that the lower repetition rate results in smoother surface of BaTiO3 thin film, and this is in good agreement with the experimental results[4]. Both of the instantaneous incident flux and number of incident atoms decrease with the increase of repetition rate. There are more chances for a monomer to diffuse and seek a suitable bonding position at higher repetition rates, therefore it is easy to read the bonding ratio increases with laser pulse repetition rate from Fig.4(b). Obviously, the control on laser pulse repetition rate is an efficient way to adjust the bonding ratio and island density for the better crystallinity and surfacial roughness.
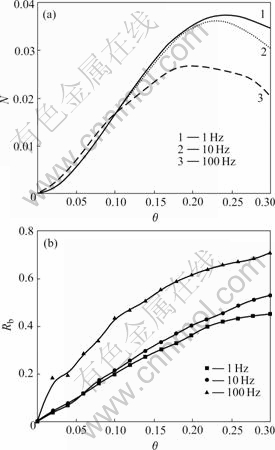
Fig.4 Island density (a) and bonding ratio (b) vs coverage at different laser pulse repetition rates
3.3 Effect of incident kinetic energy
At the various incident kinetic energies ranging from 0 to 24 eV, the relationships of the island density, bonding ratio and coverage θ, kinetic energy were investigated at T=700 K and f=1 Hz. As shown in Fig.5(a), with the increase of incident kinetic energy, the island density increases at lower coverage from 0 to 0.15 while decreases at higher coverage from 0.2 to 0.3. In Fig.5(b), the bonding ratio increases with the increase of incident kinetic energy, however it is saturated at higher coverage when Ek>12 eV. At θ=0.3, the island density and bonding ratio as functions of incident kinetic energy are summarized in Fig.5(c) to give an illustration on the effect of incident kinetic energy. With the increase of incident kinetic energy, the island density decreases except 6.2 eV<Ek<9.6 eV, and the bonding ratio increases when Ek<9.6 eV and hardly changes when Ek>9.6 eV. According to Eqn.(1), higher kinetic energy can enhance the mobility of atoms to increase the opportunities to nucleation, therefore the island density is higher at lower coverage. The higher island density will
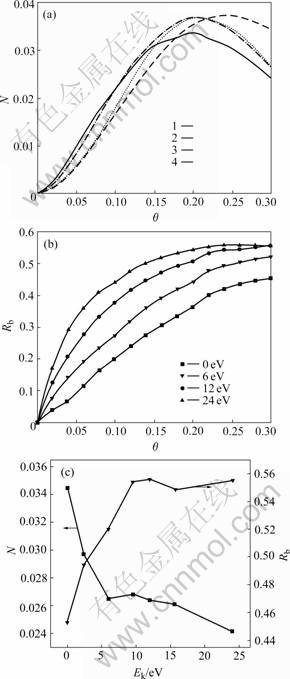
Fig.5 Island density (a) and bonding ratio (b) vs coverage, and island density and bonding ratio vs kinetic energy (c)
lead to more intensive coalescence of islands at higher coverage. This indicates that the island density decreases with the kinetic energy. The surface roughness doesn’t increase with the decrease of island density, because the kinetic energy enhances the mobility of adatoms moving to lower layers and may lead to layer-by-layer growth[15]. The bonding ratio increases with the kinetic energy, because the adatom’s mobility enhanced brings more opportunities for the adatoms to meet and bond with each other. In Fig.5(c), if the kinetic energy is large, Ek>9.6 eV, a balance is established between the capture and departure of adatoms at higher coverage 0.3, and it leads to the saturation of bonding ratio. The results suggest a way to improve BaTiO3 thin film growth by adjusting the incident kinetic energy of atoms [7].
4 Conclusions
1) The island density decreases with the increase of substrate temperature, while the bonding ratio increases with substrate temperature from 700 K to 850 K.
2) With the laser pulse repetition rate increasing, the island density decreases while the bonding ratio increases.
3) The island density decreases with the increase of incident kinetic energy except 6.2 eV<Ek<9.6 eV, and the bonding ratio increases with incident kinetic energy increasing when Ek<9.6eV and hardly changes when Ek>9.6 eV. It is worth mentioning that the control and adjustment of the preparation parameters such as the substrate temperature, laser pulse repetition rate, and incident kinetic energy are related with the island density and bonding ratio, and it will provide a useful guideline to design thin film materials with perovskite structure.
References
[1] LI Chun-ling, CUI Da-fu, ZHOU Yue-liang, LU Hui-bin, CHEN Zheng-hao, ZHANG Dao-fan, WU Fei. Asymmetric rocking curve study of the crystal structure orientations for BaTiO3 thin films grown by pulsed laser deposition [J]. Appl Surf Sci, 1998, 136: 173-177.
[2] WILLMOTT P, HUBERT J. Pulsed laser vaporization and deposition [J]. Rev Mod Phys, 2000, 72: 315-328.
[3] JENNICHES H, KLAUA M, HOCHE H, KIRSCHNER J. Comparison of pulsed laser deposition and thermal deposition: Improved layer-by-layer growth of Fe/Cu(111) [J]. Appl Phys Lett, 1996, 69: 3339-3341.
[4] KIM D H, KWOK H S. Pulsed laser deposition of BaTiO3 thin films and their optical properties [J]. Appl Phys Lett, 1995, 67: 1803-1805.
[5] EVANS J W, THIEL P A, BARTELT M C. Morphological evolution during epitaxial thin film growth: Formation of 2D islands and 3D mounds [J]. Surf Sci Rep, 2006, 61: 1-128.
[6] ITOH M. Atomic-scale homoepitaxial growth simulations of reconstructed Ⅲ-Ⅴsurfaces [J]. Prog Surf Sci, 2001, 66: 53-153.
[7] ZHANG Q L, ZHU J L, TAN J Z, YU G L, WU J G, ZhU J G, XIAO D Q. Monte Carlo simulation of the growth of SrTiO3 thin film with molecular source [J]. Vacuum, 2006, 81: 539-544.
[8] JUBERT P O, FRUCHART O, MEYER C. Nucleation and surface diffusion in pulsed laser deposition of Fe on Mo(110) [J]. Surf Sci, 2003, 522: 8-16.
[9] XU X H, ZHANG R Q, DONG X Z, GEHRING G A. A study of the optimization of parameters for pulsed laser deposition using Monte Carlo simulation [J]. Thin Solid Films, 2006, 515: 2754-2759.
[10] ZHANG Q Y, CHU P K. Study on the early stage of thin film growth in pulsed beam deposition by kinetic Monte Carlo simulation [J]. Surf Coat Technol, 2002, 158/159: 247-252.
[11] TAN X, ZHOU Y C, ZHENG X J. Dependence of morphology of pulsed-laser deposited coatings on temperature: A kinetic Monte Carlo simulation [J]. Surf Coat Technol, 2005, 197: 288-293.
[12] INABA H, HAYASHI H, SUZUKI M. Structural phase transition of perovskite oxides LaMO3 and La0.9Sr0.1MO3 with different size of B-site ions [J]. Solid State Ionics, 2001, 144: 99-108.
[13] HAYES D M. Molecular dynamics of ionic solid and liquid surfaces [J]. Phys Rev B, 1984, 30: 2182-2201
[14] HAYASHI H, SUZUKI M, INABA H. Thermal expansion of Sr-and Mg-doped LaGaO3 [J]. Solid State Ionics, 2000, 128: 131-139.
[15] SHEN J, ZHENG G, KIRSCHNER J. Growth and magnetism of metallic thin films and multilayers by pulsed-laser deposition [J]. Surf Sci Rep, 2004, 52: 163-218.
[16] GOTTMANN J, VOSSELER B, KREUTZ E W. Laser crystallization during pulsed laser deposition of barium titanate thin films at low temperatures [J]. Appl Surf Sci, 2002, 197/198: 831-838.
[17] RORMER A, ESSAHLAOUI A, PONS-Y-Moll O, VINCENT B, DEFOURNEAU R M, SEILER W, BOUDRIOUA A, MILLON E. Growth of lead titanate thin film waveguides by pulsed laser deposition [J]. Thin Solid Films, 2004, 453/454: 417-421.
[18] DU H, JOHNSON D W, JR, ZHU W, GRAEBNER J E, KAMMLOTT G W, JIN S, ROGERS J, WILLETT R, FLEMING R M. Growth and measurements of ferroelectric lead zirconate titanate on diamond by pulsed laser deposition [J]. J Appl Phys, 1999, 86: 2220-2225.
[19] HINNEMANN B, HINRICHSEN H, WOLF D E. Unusual scaling for pulsed laser deposition [J]. Phys Rev Lett, 2001, 87: 135-701.
(Edited by LI Xiang-qun)
Foundation item: Projects(10472099; 10672139) supported by the National Natural Science Foundation of China; Project(207079) supported by the Key Project of Ministry of Education of PRC; Project(05FJ2005) supported by Key Project of Scientific Technological Department of Hunan Province, China; Project(06A072) supported by the Key Project of Education Department of Hunan Province, China
Corresponding author: ZHENG Xue-jun; Tel: +86-732-8292468; E-mail: zhengxuejun@xtu.edu.cn