Adaptive controller design based on input-output signal selection for voltage source converter high voltage direct current systems to improve power system stability
来源期刊:中南大学学报(英文版)2016年第9期
论文作者:Abdolkhalegh Hamidi Jamal Beiza Ebrahim Babaei Sohrab Khanmohammadi
文章页码:2254 - 2267
Key words:input-output signal selection; online adaptive damping controller; nonlinear high voltage direct current; power system stability
Abstract: An input-output signal selection based on Phillips-Heffron model of a parallel high voltage alternative current/high voltage direct current (HVAC/HVDC) power system is presented to study power system stability. It is well known that appropriate coupling of inputs-outputs signals in the multivariable HVDC-HVAC system can improve the performance of designed supplemetary controller. In this work, different analysis techniques are used to measure controllability and observability of electromechanical oscillation mode. Also inputs–outputs interactions are considered and suggestions are drawn to select the best signal pair through the system inputs-outputs. In addition, a supplementary online adaptive controller for nonlinear HVDC to damp low frequency oscillations in a weakly connected system is proposed. The results obtained using MATLAB software show that the best output-input for damping controller design is rotor speed deviation as out put and phase angle of rectifier as in put. Also response of system equipped with adaptive damping controller based on HVDC system has appropriate performance when it is faced with faults and disturbance.
J. Cent. South Univ. (2016) 23: 2254-2267
DOI: 10.1007/s11771-016-3283-x

Abdolkhalegh Hamidi, Jamal Beiza, Ebrahim Babaei, Sohrab Khanmohammadi
Departement of Electrical Engineering, Shabestar Branch, Islamic Azad University, Shabestar, Iran
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: An input-output signal selection based on Phillips-Heffron model of a parallel high voltage alternative current/high voltage direct current (HVAC/HVDC) power system is presented to study power system stability. It is well known that appropriate coupling of inputs-outputs signals in the multivariable HVDC-HVAC system can improve the performance of designed supplemetary controller. In this work, different analysis techniques are used to measure controllability and observability of electromechanical oscillation mode. Also inputs–outputs interactions are considered and suggestions are drawn to select the best signal pair through the system inputs-outputs. In addition, a supplementary online adaptive controller for nonlinear HVDC to damp low frequency oscillations in a weakly connected system is proposed. The results obtained using MATLAB software show that the best output-input for damping controller design is rotor speed deviation as out put and phase angle of rectifier as in put. Also response of system equipped with adaptive damping controller based on HVDC system has appropriate performance when it is faced with faults and disturbance.
Key words: input-output signal selection; online adaptive damping controller; nonlinear high voltage direct current; power system stability
1 Introduction
As power demand grows rapidly and expansion in transmission and generation is restricted with the limited availability of resources and the strict environmental constraints, power systems today are much more loaded than before [1-2]. Also, steady state stability, lack of reactive power supply, voltage stability, electromechanical oscillations and transient stability are common problems that can happen in power systems expanded and transmit large amount of power over long distance transmission lines. If these long lines are used in the interconnection of power systems, poor damping of low frequency interarea oscillations and load flow problems are also very likely to happen [1-4].
Recently high voltage direct current (HVDC) systems have greatly increased. They interconnect large power systems offering numerous technical and economic advantages. This interest results from practical characteristics and performance that include for example nonsynchronous interconnection, control of power flow and modulation to increase stability limits [5]. It is well known that HVDC may improve the transient and dynamic performance of the interconnected alternative current/direct current(AC/DC) system due to its fast electronic control of power flow also transient stability of the AC systems in a composite AC-DC system can be improved by taking advantage of the fast controllability of HVDC converters [6].
Power system stability is divided in three main groups depending on the response of the system to a fault: frequency, rotor angle and voltage stability. Rotor angle stability is defined as the capability of synchronous generators to keep or restore the equilibrium between their mechanical and electromagnetic torques [7]. This stability issue is usually exhibited by synchronous generators as low frequency oscillations (LFOs). The main effects of such oscillations are to limit the power transfer capacity of the system and to cause large grid failures. This problem is used to be solved by the installation of power system stabilizers (PSSs) at synchronous generators to increase the damping of the system. Nowadays, due to recent technological advances on power system devices, damping of electromechanical oscillations has been proposed in the literature provided by HVDC links, energy storage systems, flexible AC transmission systems and wind power generation [8-13].
The conventional HVDC has several limitations and undesirable characteristics including being physically large and requiring the AC network with sufficient short- circuit ratio [14-16]. The voltage source converter based on HVDC (VSC HVDC), which uses modern semiconductors with self-commuted ability, overcomes the disadvantages of conventional HVDC and is therefore more suitable for a weak AC network or a passive network without any power sources [16].
VSCs are based on valves that can be switched on and off by a control signal using pulse width modulation (PWM) technology. PWM can generate desired waves for voltage and so offers the possibility to control both active and reactive power independently [16-17]. The control of the voltage magnitude and the phase angle of the converters makes the use of separate control for active and reactive power possible. The active power loop can be set to control either the active power or the DC-side voltage [18-19].
A power system which is equipped by VSC HVDC is a multivariable system. Inputs of converter in both sides (rectifier and inverter station) and components like generated active and reactive power, load angle and rotor speed deviation can be considered as inputs–outputs of the system. For stability purposes, one of the most important parts in supplementary controller design procedure is to select appropriate input-output coupling. Different methods to select the best feedback signal to damp power oscillations have been discussed [20-24], but the case for VSC HVDC has not been yet well covered.
In this work, a novel approach is presented to model parallel AC/DC power system namely Phillips-Heffron model based d-q algorithm in order to study system dinamical stability. In addition, a block diagram representation is formed to analyze the system stability characteristics. By this modeling approach, it is possible to analyze the small-signal stability of the system and low-frequency oscillation phenomena caused by external disturbances such as variation of input torque and fault occurring. Different controllability and observability and signal interaction analyses based on relative gain array (RGA), singular value decomposition (SVD) for power system oscillation damping are employed and best coupling is selected. Also, in order to enhance dynamical stability of power system, online adaptive controller based on self-tuning regulator (STR) is used to product a supplementary controlling signal for stabilizing and oscillation damping.
2 Configuration of power system
Figure 1 shows an SMIB system equipped with a VSC HVDC. As seen, the infinite bus is supplied by HVAC parallel connected with a VSC HVDC power transmission system. The VSC HVDC consists of two coupling transformers, two three-phase IGBT based VSCs. These two converters are connected either back- to-back or joined by a DC cable, depending on the application.
The AC side of each converter is connected to the line through a coupling transformer. The first voltage source converter behaves as a rectifier. It regulates the DC link voltage and maintains the magnitude of the voltage at the connected terminal. The second voltage source converter acts as a controlled voltage source, which controls power flow in VSC HVDC feeder. The four input control signals to the VSC HVDC are Mr, Ar, Mi and Ai, where Mr and Mi are the amplitude modulation ratio, and Ar and Ai are phase angles of the control signals of each VSC, respectively.
By applying Park’s transformation and neglecting the resistance and transients of the coupling transformers,the VSC HVDC can be modeled:
 (1)
(1)
 (2)
(2)
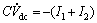 (3)
(3)
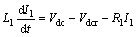 (4)
(4)
 (5)
(5)
where Vl, Vb, Ir and Ii are the middle bus voltage, infinite bus voltage, flowed current to rectifier and inverter, respectively; C and Vdc are the DC link capacitance and voltage, respectively; Cr, Ci and Vdcr, Vdci are the DC capacitances and voltages of rectifier and inverter respectively.
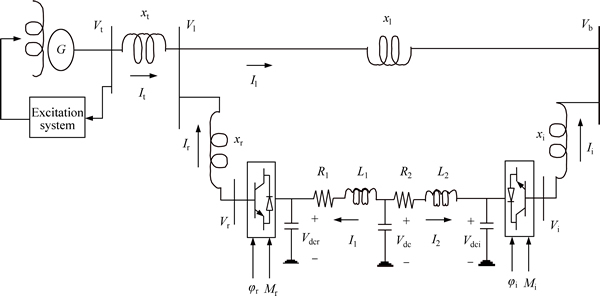
Fig. 1 SMIB system equipped with VSC HVDC
The non-linear model of the SMIB system of Fig. 1 is:
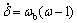 (6)
(6)
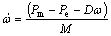 (7)
(7)
 (8)
(8)
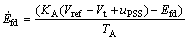 (9)
(9)
where




 Pm and Pe are the input and output power, respectively; M and D the inertia constant and damping coefficient, respectively; ωb the synchronous speed; △ and ω the rotor angle and speed, respectively;
Pm and Pe are the input and output power, respectively; M and D the inertia constant and damping coefficient, respectively; ωb the synchronous speed; △ and ω the rotor angle and speed, respectively;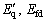 and Vt the generator internal, field and terminal voltages, respectively;
and Vt the generator internal, field and terminal voltages, respectively; 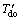 the open circuit field time constant; xd,
the open circuit field time constant; xd, 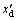 and xq the d-axis, d-axis transient reactance, and q-axis reactance, respectively; KA and TA the exciter gain and time constant, respectively; Vref the reference voltage. Also, from Fig. 1 we have:
and xq the d-axis, d-axis transient reactance, and q-axis reactance, respectively; KA and TA the exciter gain and time constant, respectively; Vref the reference voltage. Also, from Fig. 1 we have:
 (10)
(10)
 (11)
(11)
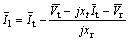 (12)
(12)
where  SUB>
SUB>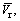
 and
and  are the armature current, rectifier voltage, infinite bus current and voltage respectively. From Eqs. (10)-(12) we can have:
are the armature current, rectifier voltage, infinite bus current and voltage respectively. From Eqs. (10)-(12) we can have:
 (13)
(13)
 (14)
(14)
 (15)
(15)
 (16)
(16)
By linearizing Eqs. (1)-(7), (13)-(16):
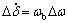 (17)
(17)
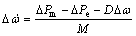 (18)
(18)
 (19)
(19)
 (20)
(20)
where
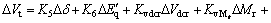
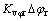 (21)
(21)

 (22)
(22)
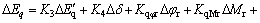
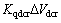 (23)
(23)
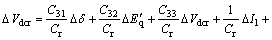
 (24)
(24)
Substituting Eqs. (21)-(23) in (17)-(20) we can obtain the state variable of the power system installed with the VSC HVDC to be(state space model):
 (25)
(25)
and


where


where △Mi, △Mr, △φi, △φr and uPSS are the linearization of the input control signals of the VSC HVDC and PSS output, respectively. The linearized dynamic model of Eq. (25) is shown in Fig. 2. In this figure, Kpu, Kqu, Kvu, Kr and Ki are defined below:

It can be seen that the configuration of the Phillips- Heffron model is exactly the same as that installed with SVC, TCSC, TCPS, UPFC and STATCOM.
Also from Eq. (25), it can be seen that there are five choices of input control signals of the VSC HVDC to superimpose on the damping function of the VSC HVDC △Mi, △Mr, △φi, △φr and uPSS. Therefore, in designing the damping controller of the VSC HVDC, besides setting its parameters, the selection of the input control signal of the VSC HVDC to superimpose on the damping function of the VSC HVDC is also important.
3 Input-output coupling: method, interactions and limitations
A significant task in the design of control systems for multivariable plants is the choice of the structure of interconnections between manipulated variables and controlled outputs and also considering interaction between different channels which couple inputs-outputs, i.e. the control configuration. In this section, methods for selecting control structure and measuring channels interaction that enable a desired performance to be achieved are considered.
3.1 Input-output coupling
Controllability shows how the state variables describing the behavior of a system can be influenced by its inputs. Observability is related with the possibility of determining the states from the outputs. More accurately, the dynamical system 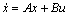 or the pair (A, B) is said to be state controllable, if for any initial state x(0)=x0 any time t1>0 and any final state x1 there exist an input u(t) such that x(t1)=x1. Otherwise, the system is said to be state uncontrollable. This system also is said observable, if for any t1>0, and initial state x(t0) can be determined from u(t1) and y(t1) [25-26].
or the pair (A, B) is said to be state controllable, if for any initial state x(0)=x0 any time t1>0 and any final state x1 there exist an input u(t) such that x(t1)=x1. Otherwise, the system is said to be state uncontrollable. This system also is said observable, if for any t1>0, and initial state x(t0) can be determined from u(t1) and y(t1) [25-26].
In damping of power oscillations, it is necessary to detemine controllability and observability for specific eigenvalues (electromechanical mode). A very powerful tool commonly used for this purpose is Popov- Belevitch_Hautus(PBH) test which is described as below.
It includes evaluating the rank of matrices:
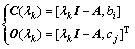 (26)
(26)
where λk is the kth eigenvalue of the matrix A, I is the identity matrix, bi is the column of B corresponding to the ith input ui and cj is the row of C corrosponding to the jth output yj. The mode λk of linear system in state space form is controllable if matrix C(λk) has full row rank. Similarly, the mode λk is observable if O(λk) is full column rank [25].
The rank of matrices C(λk) and O(λk) can be evaluated by their singular values. The singular values are defined as below: if G is a m×n complex matrix, then there exist unitary matrices U and V with dimensions of m×m and n×n, respectively, such that:
 (27)
(27)
where

Fig. 2 VSC HVDC block diagram based on Eq. (25)
 SUB>
SUB>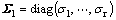
With σ1≥…≥σr≥0 where r=min{m, n}, σ1, …, σr are the singular values of G.
The minimum singular value σr represents the distance of the matrix G from all the matrices with a rank of r-1 [18]. This property can be used to quantify modal controllability and observability [14-15]. The matrix H (and J) can be written as H=[h1 h2 h3 h4] (and J=[J1 J2 J3 J4]T) where hi (and Ji) is a column (and row) vector corresponding to the ith input (jth output). The minimum singular value, σmin of the matrix [λI-A, hi] indicates the capability of the ith input to control the mode associated with the eigenvalue λ. Actually, the higher σmin, the higher the controllability of this mode by the input considered. As such, the controllability of the EM mode can be examined with all inputs in order to identify the most effective one to control the mode. The last note can also be rewritten for matrix [λkI-A, cj]T and observability of states in outputs. Thus, the choice of input and output signals through the PBH test is done by selecting those with the largest of the minimum singular values of matrices C(λk) and O(λk) [25-27].
3.2 Input-output interaction
To measure the degree of coupling or interaction in a system, the idea of relative gain array (RGA) can be employed. The original technique is based upon the open loop steady state gains of the process and is relatively simple to interpret. The relative gain array was first introduced by Bristol [25-27] at steady state as the ratio of open loop and closed loop gains between input j and output i when all output  are perfectly controlled using the inputs
are perfectly controlled using the inputs 
RGA helps to determine the pair with the highest interaction and to evaluate the possibility of using multivariable controllers. The RGA matrix Λ is defined as:
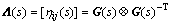 (28)
(28)
where [ηij(s)] denotes the element ij of the matrix Λ and the operator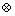 denotes the Hadamard or Schur product (element by element product).
denotes the Hadamard or Schur product (element by element product).
The following conclusions can be drawn from the RGA:
1) ηij=1, there is no interaction with other control.
2) ηij=0, manipulated input i does not affect the output j.
3) ηij=0.5, there is a high degree of interaction.
4) 0.5<ηij<1, there is an interaction between the control loops. However, this would be preferable pairing as it would minimize interactions.
5) ηij>1, the interaction reduces the effect gain of the control loop. Higher controller gains are required.
6) ηij<0, care must be taken with negative RGA elements. A negative off-diagonal element indicates that closing the loop will change the sign of effective gain.
Also the ith row sum of the RGA is equal to the squre of the ith output projection, and the jth column sum of the RGA is equal to the squre of the jth input projection. So RGA is an effective screnning tool for selecting inputs-outputs from Gall which includes all the candidate inputs and outputs.
Essentialy for the case of many candidate manipulations (inputs), one may consider not using those manipulations corresponding to coulumns in the RGA where the sum of the elements is much smaller than 1. Similarly, for the case of many candidate measured outputs (or controlled outputs) one may consider not using thoese outputs corresponding to rows in the RGA where the sum of the elements is much smaller than 1 [25].
3.3 Limitations caused by RHPZs
It is well-known that right half plane zero zeros (RHPZ) impose limitations on the achievable performance [28-29]. To guarantee closed-loop stability, the controller cannot cancel RHPZs and the frequency response of the closed-loop transfers will have fixed points that cannot be altered by the controller. For instance, the sensitivity transfer S(s) takes the value 1 at an RHPZ independently of the controller; that is, if ζ is a RHPZ, then
 (29)
(29)
These constraints become serious limitations if the RHPZs are close to the mode to be damped, since the magnitude of the closed-loop transfer cannot be arbitrarily reduced. If the controller set is reduced to proportional gains, the constraints are more serious. A simple root locus analysis reveals how strong these limitations are. Since the closed-loop poles tend to the open loop zeros, if an open loop pole is close to an RHPZ, a small increment in gain may result in an unstable system and thus it is not possible to affect the lightly damped mode. Therefore, any pair with RHPZs in the range of LFOs should be avoided. The limitations imposed by RHPZs have been used to propose input– output selection procedures in Ref. [27] in the context of damping.
4 Design of damping controller
The damping controllers are designed to produce an electrical torque in phase with the speed deviation. The four control parameters of the VSC HVDC (Mi, Mr, φi and φr) can be modulated in order to produce the damping torque.
4.1 Phase compensator method
The structure of phase compensator for VSC HVDC based damping controller is shown in Fig. 3. It consists of gain, signal washout and phase compensator blocks. The parameters of the damping controller are obtained using the phase compensation technique [6].
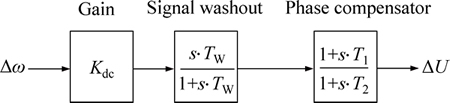
Fig. 3 Structure of HVDC based damping controller
4.2 Adaptive controller design
Intuitively, an adaptive controller is a controller that can adjust its performance in response to the altering dynamics of the process and the nature of the disturbances. In this work, an adaptive controller based on self-tuning regulator (STR) is used to produce a supplementary controlling signal for stabilizing and oscillation damping to overcome the drawbacks of conventional lead-lag controllers in nonlinear system model.
Figure 4 shows a block diagram of a process with a STR [30-31].
The block labeled “Estimation” represents an on- line estimation of the process parameters using recursive least-squares (RLS) or projection algorithms. The block labeled “Controller design” represents an on-line solution to a design problem for a system with known parameters or with estimated parameters based on minimum degree pole placement (MDPP) method. The block labeled “Controller” is to calculate the control action with the controller parameters computed by its proceeding block. The system can be viewed as an automation of processing modeling/estimation and design, in which the process model and the control design are updated at each sampling interval.

Fig. 4 Schematic of STR
Each input-output of power system can be shown as (in discrete form):
 (30)
(30)
A general linear controller can be described by:
 (31)
(31)
where R, S and T are polynomials. A block diagram of the closed-loop system is shown in Fig. 5.

Fig. 5 General linear controller with 2-degree freedom
General equations of R, S and T are polynomials and have been calculated by MDPP as follows:
 (32)
(32)
The closed-loop characteristic polynomial is thus:
 (33)
(33)
The key idea of the design method is to specify the desired closed-loop characteristic polynomial AC. The polynomial R and S can then be solved from Eq. (33). In the design procedure we consider polynomial AC to be a design parameter that is chosen to give desired properties to the closed-loop system. Equation (33), which plays a fundamental role in algebra, is called the Diophantine equation. For more detail about designing this kind of controller, readers can refer to Refs. [30-31]. Simulation steps are as follows:
Data: Give the reference model in the form of a desired closed-loop pulse transfer operator Bm/Am (desire transfer function) and a desired polynomial A0.
Step 1: Estimate the coefficients of the polynomials A and B using the RLS method.
Step 2: Using the polynomials A and B estimated in Step 1; apply the MDPP method, the polynomials R, S and T of the controller are then obtained by solving the Diophantine equation.
Step 3: Compute the control action which is Ru(t)=Tuc(t)-Sy(t). Repeat steps 1-3 at each sampling period.
5 Simulation results
Power system information is given in appendix A. Constant coefficients in Eq. (25) are calcuated according to informations given in appendix B. In this work, we consider four outputs which are △, ω, Pe and Qe i.e. load angle, rotor speed deviation, active and reactive power and four inputs which are Mr, φr, Mi and φi i.e. modulation index and angle of rectifier and inverter, respectively. There is another input related to power system stabilizer which in this work is omitted. So, system matrix G(s) is a 4×5 matrix. Selecting an affective coupling between inputs-ouputs for damping oscillation of the power system is one of the most imporatant goals of this work. Following section consider this topic.
5.1 Controllability and observability measure
SVD based on PBH is employed to measure the controllability and observability of the electromechanical mode (EM) mode from each of the four inputs: Mr, φr, Mi and φi. The minimum singular value σmin is estimated over a wide range of operating conditions. For SVD analysis, Pe ranges from 0.01 to 1.5 per unit (PU) and Qe=[-0.3, 0, 0.3]. Under each loading condition, the system model is linearized, the EM mode is identified, and the SVD-based controllability and observability measure is implemented. For comparison purposes, the minimum singular value for all inputs at Qe=-0.3, 0.0 and 0.3 Pu is shown in Fig. 6, respectively. From these figures, the following can be noticed:

Fig. 6 Observability (a) and controllability (b) of simulation
1) EM mode controllability via φr is always higher than that of any other inputs.
2) The capabilities of φr, Mr and φi to control the EM mode is higher than that of Mi.
3) All control signals have low EM mode controllability in low load condition except φr.
4) Observability of △ is always higher than that of any other outputs.
5) The observability of △, Pe and Qe is higher than that of ω.
5.2 Selecting candidate for coupling
RGA is employed to select the appropriate input- output for the purpose of designing the damping adaptive controller. First Pe ranges from 0.01 to 1.1 Pu and Qe=constant. The electromechanical mode for every work point is calculated. At this frequency, RGA matrix is calculated and row-column sum is computed.
The results are depicted in Fig. 7. According to Fig. 7, Mr and φr are from inputs and △ and Qe are appropriate inputs-outputs for coupling and designing damping controller because of what illustrated in section 3.2. But in this part, another imporatant factor which must be taken into account is RHPZs. RHPZs can affect the controller performance and maybe lead to an unstable system. So in the next setion, position and distance of system zeros from electromechanical mode willbe considered.
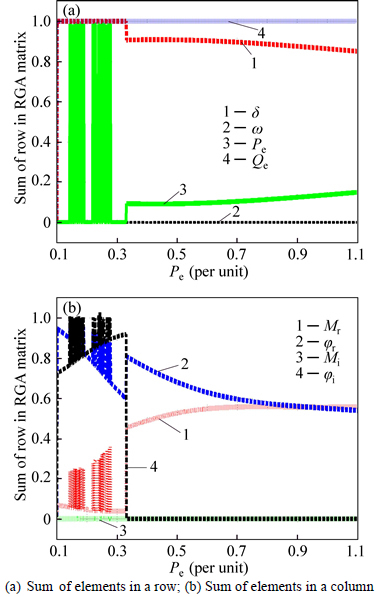
Fig. 7 RGA analysis on electromechanical mode:
5.3 Limitations of RHPZs
Figure 8 demonstrates the geometric distance between RHPZs of the system with electromechanical mode. As discussed in section 3.2, RHPZs can degrade feedback performance. RHPZs limit the achievable performance of a feedback loop by limiting the open- loop gain bandwidth product. They can be a cause of concern particularly if they lie within the closed loop bandwidth one is aiming for. The choice of outputs should be such that a minimum number of RHP zeros is encountered and should be as far removed from the imaginary axis as possible.
According to Fig. 8, channel between ω and rectifier inputs has appropriate distance of RHPZs. Thus, adaptive supplementary controller will be designed between ω and φr (g22) where gij is transfer function between output i and input j.
5.4 Proposed adaptive supplementary controllers for nonlinear system
In this work, an adaptive controller based on STR is designed between ω and φr and simulated by using S-function under the SIMULINK/MATLAB software. Controller parameters are given in appendix A. Samplingtime for this simulation is T=0. 1 s.
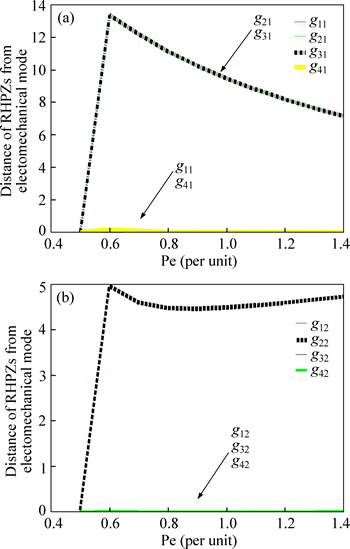
Fig. 8 RHPZs distance to electromechanical mode
To assess the effectiveness of the proposed stabilizers two different conditions are considered according to Table 1. Rotor speed deviation, load angle and active power for suddenly change in input power (△Pm=0.2 pu) at t=25T and three phase short circuit during seven cycles on infinite bus at t=50T are shown in Figs. 9 and 10.
Table 1 Load condition

Figures 9(b), (e) and 10(b), (e) show parameters of designed plant estimator (ai and bi). The plant to be estimated is in the general form as 
 and d=1 is the time delay. Also Figs. 9(c) and 10(c) show coefficient of R and S which construct adaptive controller for the power system.
and d=1 is the time delay. Also Figs. 9(c) and 10(c) show coefficient of R and S which construct adaptive controller for the power system.
Changing in mechanical power which is applied to rotor by turbine, can be considered as a disturbance for power system. Since synchronous generators operate at synchronous speed, the speed deviation is zero under normal operating conditions. But the speed is also disturbed when a fault occurs or a disturbance applied to system. Figures 9(f) and 10(f) show the speed deviation response of the synchronous generator with an adaptive controller which zero speed deviation is obtained during the post-fault steady-state operation.
A three-phase fault is the most severe disturbance in a power system and the simulation is carried out by applying a symmetrical three-phase. This fault occurs at t=5 s (25T) and clears at t=5 s+7. In the case of a three-phase fault at the infinite bus terminal of the power system, the generator will not supply any power during the faulted condition. Moreover, the system may become unstable during the post-fault period due to the insufficient damping provided by the excitation system. Conventional power system stabilizers (CPSSs) are unable to provide adequate damping into the system. But the designed adaptive controller provides adequate damping to settle the rotor angle, speed deviation, and terminal voltage to their pre-fault values after the clearance of the fault (Figs. 9(a), (b), (f), (g) and Figs. 10(a), (b), (f), (g)).
Another important factor in transient stability analysis is the post-fault steady-state voltage. Since the stability of the considered test system is dominated by the rotor angle and speed dynamics, the voltage stability will be unaffected by external disturbances if the stability issues related to the rotor angle and the speed is ensured.
6 Conclusions
1) A dynamic model based VSC HVDC is considered and a supplementary adaptive online controller is designed to improve power system stability and oscillation damping.
2) SVD and RGA have been employed to evaluate the EM mode controllability and observability to the four inputs and also appropriate coupling.
3) Results show that the best output-input for damping controller design is rotor speed deviation-phase angle of rectifier respectively.
4) Response of system which is equipped with adaptive damping controller based on HVDC system, has appropriate performance when it is faced with faults and disturbance.
Appendix A
The test system parameters are (all in Pu):
Machine and exciter:
xd=1, xq=0.6, x′d=0.3,
D=0, M=8, T′do=5.044, freq=60,
vref=1, KA=120, TA=0.015
Transmission line and transformer reactance:
xt=0.1, xl=1, xr=xi=0.15
VSC HVDC:
Vdcr=2, Vdci=1.95,
Cr=Ci=2,
L1=L2=0.09, C=0.09

Fig. 9 Responses of power system equipped by HVDC system and supplementary adaptive controller in heavy loading:
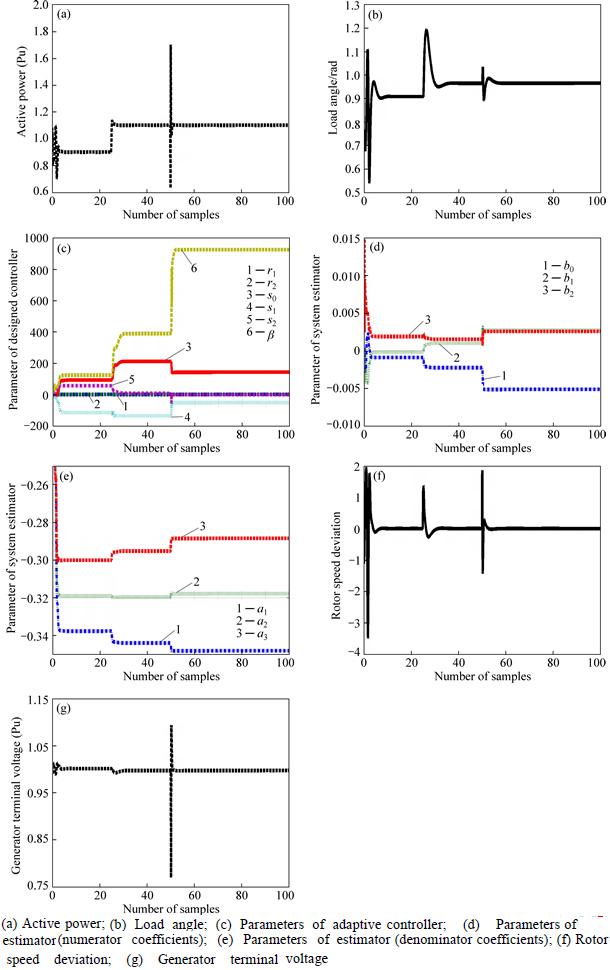
Fig. 10 Responses of power system equipped by HVDC system and supplementary adaptive controller in nominal loading:
Appendix B
Coefficients:
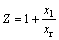
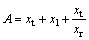

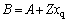
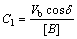

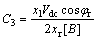
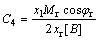

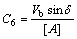
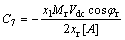

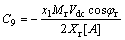
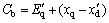


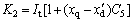
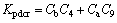

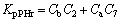



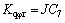
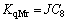




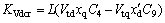
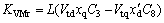











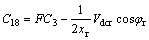





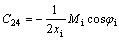

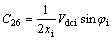
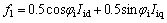
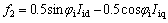
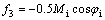


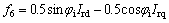
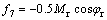

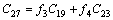

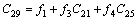
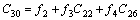
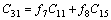
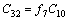
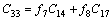
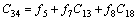

References
[1] ADAPA R. High-wire act: HVDC technology: The state of the art [J]. IEEE Power Energy Mag, 2012, 10(6): 18-29.
[2] PREECE R, ALMUTAIRI A, MARJANOVIC O, MILANOVIC J. Damping of electromechanical oscillations by VSC-HVDC active power modulation with supplementary wams based modal LQG controller [C]// IEEE Power Energy Soc Gen Meeting. San Diego, CA, USA, 2011: 1-7.
[3] ZHANG L, HARNEFORS L, NEE H-P. Interconnection of two very weak ac systems by VSC-HVDC links using power-synchronization control [J]. IEEE Trans Power Syst, 2011, 26(1): 344-355.
[4] LATORRE H F, GHANDHARI M. Improvement of power system stability by using a VSC-HVDC [J]. Electrical Power and Energy Systems, 2011, 33: 332-339.
[5]  S, LARSSON M, MORARI M. Grid stabilizationthrough VSC-HVDC using wide area measurements [C]// IEEE Powertech, Power Syst Technol Trondheim. Norway, 2011: 1-6.
S, LARSSON M, MORARI M. Grid stabilizationthrough VSC-HVDC using wide area measurements [C]// IEEE Powertech, Power Syst Technol Trondheim. Norway, 2011: 1-6.
[6] BANAEI M, TAHERI N. An adaptive neural damping controller for HVDC transmission systems [J]. Euro Trans Electr Power, DOI: 10.1002/etep.485.
[7] KUNDUR P. Power system stability and control [M]. Columbus, USA: McGraw-Hill Professional, 1994.
[8] PIPELZADEH Y, CHAUDHURI N, CHAUDHURI B, GREEN T. System stability improvement through optimal control allocation in vsc-based hvdc links [J]. IET Gener Transm Distrib, 2012, 6(9): 811-821.
[9]  F, SUMPER A, GOMIS-BELLMUNT O, VILLAFAFILA-ROBLES R. A review of energy storage technologies for wind power applications [J]. Renew Sustain Energy Rev, 2012, 16(4): 2154-2171.
F, SUMPER A, GOMIS-BELLMUNT O, VILLAFAFILA-ROBLES R. A review of energy storage technologies for wind power applications [J]. Renew Sustain Energy Rev, 2012, 16(4): 2154-2171.
[10]  J L, BIANCHI F, GOMIS-BELLMUNT O. Analysis of the damping contribution of power system stabilisers driving wind power plants [J]. Wind Energy, 2014, 17(2): 267-278.
J L, BIANCHI F, GOMIS-BELLMUNT O. Analysis of the damping contribution of power system stabilisers driving wind power plants [J]. Wind Energy, 2014, 17(2): 267-278.
[11] IMHOF M, ANDERSSON G. Dynamic modeling of a VSC-HVDC conv [C]// 48th Int Univ Power Eng Conf. Dublin, Ireland, 2013, 1-6.
[12] MOKHTARI M, KHAZAEI J, NAZARPOUR D. Sub-synchronous resonance damping via doubly fed induction generator [J]. Int J Electr Power Energy Syst, 2013, 53: 876-883.
[13] de PRADA-GIL M, MANCILLA-DAVID F,  J L, MULJADI E, SINGH M, GOMIS-BELLMUNT O, SUMPER A. Contribution of type-2 wind turbines to subsynchronous resonance damping [J]. Int J Electr Power Energy Syst, 2014, 55: 714-722.
J L, MULJADI E, SINGH M, GOMIS-BELLMUNT O, SUMPER A. Contribution of type-2 wind turbines to subsynchronous resonance damping [J]. Int J Electr Power Energy Syst, 2014, 55: 714-722.
[14] GUO C, ZHAO C. Supply of an entirely passive AC network through a doubleinfeed HVDC system [J]. IEEE Trans Power Electron, 2010, 25(11): 2835-2841.
[15] ZHANG L. Modeling and control of VSC-HVDC links connected to weak AC systems [D]. Stockholm, Sweden: Dept Elect Eng, Royal Inst Technol, 2010.
[16] TANG X, LU D. Enhancement of voltage quality in a passive network supplied by a VSC-HVDC transmission under disturbances [J]. Power and Energy Systems, 2014, 54: 45-54.
[17] LI Y, ZHANG Z W, REHTANZ C. A new voltage source converter-HVDC transmission system based on an inductive filtering method [J]. IET Trans Gener Transm Distrib, 2012, 6(9): 569-576.
[18] ROBIN P, JOVICA V M. Tuning of a damping controller for multiterminal VSC-HVDC grids using the probabilistic collocation method [J]. IEEE Trans Power Delivery, 2014, 29(1): 318-326.
[19] mc NAMARA P, NEGENBORN R R, de SCHUTTER B, LIGHTBODY G. Optimal coordination of a multiple hvdc link system using centralized and distributed control [J]. IEEE Trans Control Syst Technol, 2013, 21(2): 302-314.
[20] PORDANJANI I R, XU W. A singular value decomposition-based technique for decoupling and analyzing power networks [J]. International Journal of Electrical Power & Energy Systems, 2016, 74: 265-273.
[21] ATALIK T, DOGAN M, DEMIRCI T. Design and implementation of an identifier system for inter-area power oscillations [J]. Electric Power Systems Research, 2015, 122: 86-95.
[22] TANG K, GANESH K. Venayagamoorthy. Damping inter-area oscillations using virtual generator based power system stabilizer [J]. Electric Power Systems Research, 2015, 129: 126-141.
[23] MAGAJI N, MUSTAFA M. Optimal location and signal selection of UPFC device for damping oscillation [J]. Int J Electr Power Energy Syst, 2011, 33(4): 1031-1042.
[24] REZAEI N, KALANTAR M, SHAYANFAR A, ALIPOURI Y, SAFARI A. Optimal IPFC signal selection and damping controller design using a novel current injection model in a multi-machin [J]. Int J Electr Power Energy Syst, 2011, 33(5): 1042-1055.
[25] SKOGESTAD S, POSTLETHWAITE I. Multivariable feedback control–analysis and design [M]. Chichester, UK: John Wiley & Sons, 2007.
[26] PANDA S, YEGIREDDY N K. Multi-input single output sssc based damping controller design by a hybrid improved differential evolution-pattern search approach [J]. ISA Transactions, 2015, 58: 173-185.
[27] SUJATHA V, PANDA R C. Control configuration selection for multi input multi output processes [J]. Journal of Process Control, 2013, 23(10): 1567-1574.
[28] GUO J C, PENG Y W. The control method of multivariable time-delay square system containing right half plane zeros [J]. Procedia Engineering, 2011, 15: 1004-1009.
[29]  J L, BERENGUEL M,
J L, BERENGUEL M,  T. Optimal feedforward compensators for systems with right-half plane zeros [J]. Journal of Process Control, 2014, 24(4): 368-374.
T. Optimal feedforward compensators for systems with right-half plane zeros [J]. Journal of Process Control, 2014, 24(4): 368-374.
[30] ABBAS K, MASOUD H F. An adaptive set-point modulation technique to enhance the performance of load frequency controllers in a multi-area power system [J]. Journal of Electrical Systems and Information Technology, 2015, 2(3): 391-405.
[31] BANAEI M, HASHEMI A. An adaptive UPFC based stabilizer for damping of low frequency oscillation [J]. Journal of Electrical Engineering & Technology, 2010, 5(2): 197-208.
(Edited by FANG Jing-hua)
Received date: 2015-07-21; Accepted date: 2015-11-30
Corresponding author: Abdolkhalegh Hamidi, PhD Candidate; Tel: +98-7431162247; E-mail: isi.hamidi@gmail.com

