J. Cent. South Univ. Technol. (2011) 18: 266-270
DOI: 10.1007/s11771-011-0689-3
Operation reliability for on-ramp junction of urban freeway
CI Yu-sheng(慈玉生)1, 2, WU Li-na(吴丽娜)3, 4, LING Xian-zhang(凌贤长)2, PEI Yu-long(裴玉龙)1
1. School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin 150090, China;
2. Postdoctoral Station of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China;
3. Department of Automobile, Heilongjiang Institute of Technology, Harbin 150050, China;
4. College of Traffic, Northeast Forestry University, Harbin 150040, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract: A disorder situation of traffic operation always appears in on-ramp junction area of urban freeway, because the operation action for vehicles presents the weaving condition, especially for different vehicle types. Based on the analysis on the cellular automata theory, and combining with on-site survey data, several key parameters were defined, namely, cellular length, cellular speed, cellular acceleration, updating time interval. In addition, cellular acceleration rule, cellular deceleration rule, random rule, lane-changing rule and other micro-simulation rules were set, and cellular automaton micro-simulation model was set up. Further- more, a micro-simulation module was developed for traffic operation actions of on-ramp junction with Matlab toolbox. Finally, a simulation experiment for traffic operation reliability was done with this micro-simulation module, and the situation of change for on-ramp junction area was obtained under the conditions of different mainline design speed, acceleration lane length, vehicle generation probability and lane-changing probability. The results show that operation reliability for on-ramp junction is determined by the parameters of the probability of vehicle generation and the length of acceleration lane, especially for on-ramp.
Key words: on-ramp junction; operation reliability; cellular automata; simulation model
1 Introduction
Traffic behavior for single vehicle cannot be represented by macroscopic models in traffic wave and gap-acceptance theory. However, this aim can be perfectly realized by cellular automata model through a microscopic and discrete pattern to simulate the kinestate of traffic stream of the individual vehicle.
Nagel-Schreckenberg (NS) model was firstly put forward by NAGEL and SCHRECHENBERG [1], which was used to describe the traffic stream on a highway with just one-dimensional stochastic cellular automaton model at that time. Combining with hydro-dynamic theory, LIGHTHILL and WHITHAM [2] developed a simple continuous model, which was frequently used to investigate the traffic stream characteristics in the road ramp areas. BANKS [3] reported that queues first formed in the median lane at a location well in advance of the on-ramp. CASSIDY and BERTINI [4] reported that bottlenecks activate some distance downstreams of on-ramps, which could be explained by lane-changing behavior. HELBING and SCHRECHENBERG [5], WOLF [6], and DONG et al [7] used cellular automata to carry out the traffic stream simulation experiments. EVANS et al [8] studied the probability distribution of the time of breakdown on a freeway. They applied Markov chains to develop the probability distribution of the time of breakdown via the zonal merging probabilities with respect to the vehicles travelling on the throughway. CASSIDY et al [9] studied the freeway traffic near an off-ramp, and the ramp queues were confined to right-most exit lane. Non-exiting drivers slowed down upon seeing these queues and this diminished flows in all lanes, and also the lengths of these exit queues were negatively correlated with the discharge flows in the adjacent lanes of the freeway segment. HIDAS [10] introduced a micro-simulation model of traffic network to analyze the lane-changing behaviors in the cases of free-flow and forced-flow, which showed the shortages of the expressway due to the limited capacity in on-ramp junctions. BERTINI and CASSIDY [11] used surveying data to study queue discharge features at a freeway bottleneck on downstream of a merge. GUO and ZHANG [12] studied the reliability of road capacity under the conditions of different arrival rate, right turn rate and priority rate. PENG et al [13] proposed a simulation model of road-network flows based on the advantages of both ant colony optimization and multi-agent system to improve the autonomy, cooperation and indetermination of vehicles in the process of choosing paths for better simulation effect. CASSIDY and RUDJANAKANO- KNAD [14] showed that metering an on-ramp can recover the higher discharge flow at a merge and thereby increase the merge capacity. PEI and CI [15], and CI et al [16] applied numerical simulation method to study on- and off-junctions traffic stream characteristics.
However, there still remains some unsolved questions, despite of various efforts in this field. Upon the urgent requirement, the primary focus of this study is to address the traffic stream simulation for on-ramp junction by two-dimensional cellular automata model to evaluate the operation reliability issue.
2 Model and strategies
2.1 Model description
There is an acceleration lane at on-ramp junction, for the traffic conflict here, actually being the lane changing problems of vehicles within limited length. Namely ramp vehicles change lanes from acceleration lane to shoulder lane, and then travel in the shoulder lane, as shown in the simplified form in Fig.1. We just consider the shoulder lane of mainline. For brief consideration, the upstream and downstream sections of on-ramp junction are marked by U and D, and R for the ramp section. In this study, the length of acceleration is Lw and vehicles merge in this area following the corresponding lane-changing conditions. Otherwise, vehicles would update the state under the rules of single lane NS model beyond the speed-up area.
Fig.1 Cellular frame for on-ramp junction
Lane-changing behaviors at on-ramp junction are mandatory lane-changing, thus they confront relative simple lane-changing conditions. Each time interval is subdivided into two sub-steps with two-lane model by the procedure of updating location. In the first sub-step, parallel lane-changing is fulfilled in the satisfied lane-changing condition. In the latter case, vehicles update locations under the rule of single-lane NS model. Imperative lane-changing is applied to deal with ramp traffic stream. Thus, all vehicles, conforming to the above-mentioned lane-changing principle, transferred to main lane at road section Lw. Since the NS cellular of low order end at acceleration lane is fixed by the stiffness boundary to vehicles in ramp, vehicles have to stop and wait for other chances of lane-changing, if they do not succeed in lane-changing while reaching this NS cellular. Therefore, the probability of lane-changing is considered as 1. For discretionary lane-changing actions, vehicles from shoulder lane of upstream and median lane of downstream in mainline would take lane-changing action with a probability of Pc.
2.2 Parameters
2.2.1 Length of cellular
Initially, urban freeway system is separated into many cells with length L, and a vehicle is contained in one cell. So, the length of a cell just equals the average space headway. Traffic jam density for ramp junctions is nearly 120-145 passenger car unit (pcu)/km, and the preliminary length of cell is determined as 7 m. If so, a random vehicle speed-up moving, with the acceleration value of 1 L/s2 just equal 7 m/s2. As we know, this acceleration value will be almost the maximum acceleration value of vehicles. Therefore, vehicles will always move with the maximum acceleration and deceleration values. Obviously, it is not suitable for the actual traffic occasion.
Therefore, the length of a cell, one of key parameters for simulation model, is just 1/7 of average space headway, which is 1 m for a cell. Namely, continuous seven cells contain a vehicle.
2.2.2 Value of maximum speed
Vehicles in on-ramp junction are always influenced by in-flow from ramp. Thus, traveling speed is always below the design speed, and the maximum speed is approximately equal to free-flow speed (FFS).
Therefore, the maximum speed in this simulation model is 90 km/h, namely, the maximum speed of cellular automata (vmax) is equal to 25 m/s, and the range of speed is between 0 and vmax.
2.2.3 Values of maximum acceleration and deceleration
According to the dynamic principle of the vehicle, whether vehicles could arrive at the maximum value or not just depends on the road attachment coefficient (μr) in the process of acceleration and deceleration.
So, values of the maximum acceleration and deceleration (±amax) are set as ±7 m/s2 in this simulation model, including 7 m/s2 for the maximum acceleration and -7 m/s2 for the deceleration, respectively.
2.2.4 Updating time interval
Updating time interval is also a key parameter and is set to be 0.5 s in this study. By considering the actual situation of traffic stream, the values for vehicle speed and acceleration, acceleration and deceleration will have a rapid change, if the updating time interval is longer.
2.2.5 Boundary conditions
In order to guarantee the traffic stream simulation stability and good effect for the special segment of researched freeway, a closed freeway system is selected for the boundary conditions of NS model.
In the model, the system is an unblocked freeway with source and export. Vehicles are generated in the ramp and the left boundary of mainline, and they would not be considered beyond the research area.
2.3 Operation rules
2.3.1 Acceleration rule
At the moment of t, if vn(t)≤gn(t), vehicles will get an acceleration an(t)
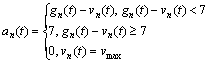(1)
where an(t) is the acceleration of present vehicle between time t and t+1; vn(t) represents the speed of present vehicle at the moment of t; gn(t) represents the interval between the head of the present vehicle and the tail of the front vehicle at the moment of t, that is, gn(t)=xn-1(t)- xn(t)-7, where xn-1(t) and xn(t) represent the locations of the front vehicle and the present vehicle at the moment of t, respectively.
2.3.2 Deceleration rule
At the moment of t, if vn(t)>gn(t), vehicles will decelerate following the mode of
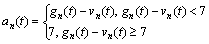(2)
2.3.3 Adjustment rule
At the moment of t, acceleration for present vehicle is known, and the deceleration for front vehicle is assumed the maximum deceleration -7 m/s2, so at the moment of t+1:
If vn(t+1)≤gn(t+1), then the acceleration for the present vehicle remains the same as an(t);
If vn(t+1)>gn(t+1), then an(t)=an(t)-1≥-7, and it does not compute vn(t+1) and gn(t+1) until vn(t+1)≤ gn(t+1). The an(t) is modified to actual acceleration for the present vehicle at the moment of t.
2.3.4 Random rule
Under the condition of probability of Pb, vehicles from adjustment for adjustment rules would still slow down. The deceleration incrimination is ?a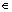
[-7, 0] m/s2, and also the adjustment deceleration plus ?a is beyond the maximum deceleration.
2.3.5 Updating rule
Cells are updated continuously according to the speed obtained from the former time:
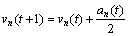(3)
(4)
where xn(t) represents the location of present vehicle at the moment of t.
2.3.6 Lane-changing rule
Postulating the location x0(t) for target vehicle A and xn-1(t), xn(t) for the front and rear vehicles in left or right lane locations. If the target vehicle satisfies the following condition:
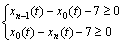(5)
then, the target vehicle will change lanes with a certain probability. That is to say, target vehicle will change lanes and finally update location with model rules if the cell for left or right lane is not filled.
3 System development
The procedure for traffic stream simulation of cellular automata includes five steps: network setting, initial state setting, cell speed and locations updating, simulation image generating and traffic stream analysis. Fig.2 shows the module frame of cellular automata simulation.
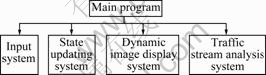
Fig.2 Module frame of cellular automata simulation
3.1 Vehicle generation module
We must first get a satisfied demand and adequate actual traffic stream input, that is, the vehicle generation module. At the moment of simulation, vehicles are generated continually at the left boundary cross-sections of ramp and mainline, which reflects the randomness of system initialization including the factors of vehicles themselves and arriving time.
This module is divided into two parts: vehicles random generation and initial state producing. First, a constant P is set as [0, 1], and generates a random number according to the function of weibrnd (0.8, 2.6, 10000, 1). Finally, a vehicle is to be generated with a speed assigned in the range of [0, vmax], if the all cells are full, compared with the two values and the front n cells.
3.2 State updating module
This module is one of the most important components of this simulation system, which impacts the simulation results directly.
Just because of the different characteristics of operation speeds for different design speeds, values for the maximum speed and acceleration are set, and also for lane-changing and random probabilities. According to updating time interval set, the speed, acceleration and location updating for each cell are also set in the initialization.
Cells in mainline and acceleration lane have different maximum speeds, and also according to different ramp areas, vehicles in different lanes have different lane-changing directions and probabilities.
3.3 Simulation image display module
Fig.3 shows the cellular automata simulation interface for ramp junctions. The output for simulation result is shown by image and numerical value. The simulation image display module also helps to judge the rationality of simulation model.
Just because the simulation updating depends on time interval, simulation image is noncontinuous. The critical image is developed for every time interval to realize the vehicles moving forward operation.
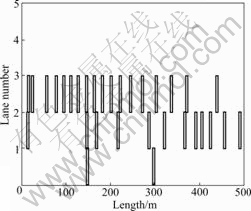
Fig.3 Cellular automata simulation interface for ramp junctions
3.4 Traffic operation analysis module
This module is set for calculating traffic flow rate, speed and density beyond every time interval.
Traffic stream variability for upstream, downstream and on-ramp is analyzed, and also that for densities and speed of speed change lane and mainline is analyzed.
4 Simulation experiment and results
Before testing the simulation experiments, several parameters should be determined as the input, such as length of ramp junction, updating time interval, vehicles generation rate, lane-changing rate, the maximum ac- and deceleration and the maximum speed.
The inputs were: 1) The length of ramp junction is between 330 and 680 m, compared with length of speed change lane (50-400 m); 2) The design speed for mainline are 60, 80 and 100 km/h, meaning that the maximum speeds for cells in mainline and ramp are [19, 22, 25] and [11, 14, 20] m/s; 3) The maximum acceleration is 7 m/s2; 4) The probability of vehicle generation and lane-changing belongs to [0, 1]; 5) The random changing probability is 0.2; 6) The updating time interval is 0.5 s, and the simulation time is 7 500 s.
Based on several experiments, an actual traffic flow rate diagram for different speeds is shown in Fig.4, in which vehicle generation probability is 0.3, lane- changing probability for mainline is 0.2, lane-changing probability for acceleration lane is 1, and the length of ramp junction is 500 m.
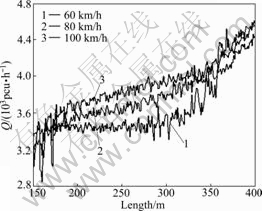
Fig.4 Traffic stream simulation result for on-ramp junction
An actual traffic flow rate diagram is acquired for different lengths of acceleration lane, as shown in Fig.5, which is based on the probability for vehicles generation and lane-changing of 0.2.
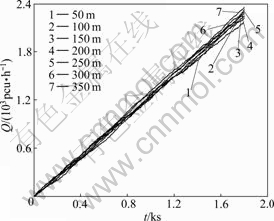
Fig.5 Influence for on-ramp junction in different lengths of acceleration lane
In this work, in-flow volume Qi is the number of vehicles through a cross section of mainline. Fig.6 shows the relationship between generation probability and in-flow probability with the maximum speed for mainline vmax=22 and ramp vmax=14.
It can be found that with the increase of P, and also the increase of ramp and mainline flow, the ramp inflow gradually increases as changing lanes in time. The mainline inflow probability increases when vehicles of mainline lanes are not heavy (P≤0.3).
However, when vehicles volume of mainline lanes are very heavy, as more and more vehicles of the ramp change lanes, the upstream traffic of mainline becomes more difficult to go through, and the inflow will gradually decrease and when P=0.9, the inflow just falls to only about 200 h-1, nearly a jam condition.
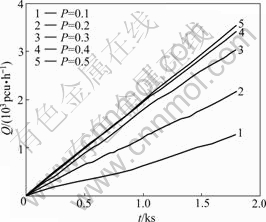
Fig.6 Tendency chart of mainline with inflow probability
5 Conclusions
1) A micro-simulation cellular automaton model is set up, which includes model simplified representation, parameters choice and operation rules.
2) A simulation system module is developed, with four sub-modules included.
3) Simulation experiments are done and traffic operation reliability conditions are obtained. The operation reliability for on-ramp junction is determined by the parameters of the probability of vehicle generation and the length of acceleration lane.
References
[1] NAGEL K, SCHRECHENBERG M. A cellular automaton model for freeway traffic [J]. J Phys I France, 1992, 2: 2221-2229.
[2] LIGHTHILL M J, WHITHAM G B. A theory of traffic flow on long crowded roads [J]. Proc Roy Soc, 1955, 229: 317-345.
[3] BANKS J H. Flow processes at a freeway bottleneck [J]. Transportation Research Record 1287, 1990: 20-28.
[4] CASSIDY M J, BERTINI R L. Some traffic features at freeway bottlenecks [J]. Transportation Research: Part B, 1999, 32: 49-59.
[5] HELBING D, SCHRECHENBERG M. Cellular automata simulating experimental properties of traffic flow [J]. Phys Rev E, 1999, 59(3): 2505-2508.
[6] WOLF D E. Cellular automata for traffic simulations [J]. Physica A, 1999, 263: 438-451.
[7] DONG Li-yun, XUE Yu, DAI Shi-qiang. One-dimensional cellular automation model of traffic flow based on car-following idea [J]. Applied Mathematics and Mechanics, 2002, 123(4): 363-370.
[8] EVANS J L, ELEFTEIADOU L, GAUTAM N. Probability of breakdown at freeway merges using Markov chains [J]. Transportation Research: Part B, 2001, 35: 237-254.
[9] CASSIDY M J, ANANI S B, HAIGWOOD J M. Study of freeway traffic near an off-ramp [J]. Transportation Research: Part A, 2002, 36: 563-572.
[10] HIDAS P. Modeling lane changing and merging in microscopic traffic simulation [J]. Transportation Research: Part C, 2002, 10: 351-371.
[11] BERTINI R L, CASSIDY M J. Some observed queue discharge features at a freeway bottleneck downstream of a merge [J]. Transportation Research: Part A, 2002, 36: 683-697.
[12] GUO Chang-bo, ZHANG Ning. Simulation study on the road capacity reliability of thruway with exit [J]. Journal of System Simulation, 2003, 15(11): 1595-1599. (in Chinese)
[13] PENG Min-jing, LIN Jian, XIAO Jian-hua. Simulation model of road-network flows based on ACO and MAS [J]. Journal of Central South University: Science and Technology, 2005, 36(s): 581-585. (in Chinese)
[14] CASSIDY M J, RUDJANAKANOKNAD R. Increasing the capacity of an isolated merge by metering its on-ramp [J]. Transportation Research: Part B, 2005, 39: 896-913.
[15] PEI Yu-long, CI Yu-sheng. Study on traffic flow at on-ramp junctions in urban freeway with cellular automaton model [C]// Proceedings of 2007 International Conference on Management Science & Engineering. Harbin, 2007: 2253-2257.
[16] CI Yu-sheng, WU Li-na, PEI Yu-long, LING Xian-zhang. A new cellular automaton traffic flow model for an off-ramp junction of a Chinese urban expressway [C]// Proceedings of the 9th International Conference of Chinese Transportation Professionals. Harbin, 2009: 1870-1876.
(Edited by LIU Hua-sen)
Foundation item: Project(HIT.NSRIF.2009102) supported by the Fundamental Research Funds for the Central Universities in China; Project(11541295) supported by the Scientific Research Fund of Heilongjiang Provincial Education Department of China; Project(20100471029) supported by China Postdoctoral Science Foundation
Received date: 2009-11-13; Accepted date: 2010-06-25
Corresponding author: CI Yu-sheng, PhD; Tel: +86-451-86282117; E-mail: ciyusheng1999@126.com
