导流式铝电解槽电-热平衡计算建模与应用
周乃君，童道辉，张家奇，王瑞雪
(中南大学 能源科学与工程学院，湖南 长沙，410083)
摘要：采用经验公式与数值计算相结合的方法建立导流槽电平衡及能量平衡计算模型，针对1台114.5 kA系列槽进行计算，得到槽体电-热场的分布和槽膛内形的相关信息。研究结果表明：在设定的工艺条件下，导流槽的槽极距可降至2.75 cm，体系电压可降至3.312 V，铝电解能量利用率提高到53.63%，体现了导流槽的极大节能潜力。在计算工况下，导流槽也能获得形状规整的槽帮，稳态时槽帮厚度可达12 cm左右。该计算模型和计算结果可为导流槽的设计提供参考。
关键词：导流槽；电-热平衡；仿真建模；有限元分析
中图分类号：TF806.25 文献标志码：A 文章编号：1672-7207(2011)12-3888-06
Modeling and application for calculation of electric-thermal balance in a drained aluminium reduction cell
ZHOU Nai-jun, TONG Dao-hui, ZHANG Jia-qi, WANG Rui-xue
(School of Energy Science and Engineering, Central South University, Changsha 410083, China)
Abstract: The model for calculating of electric-thermal balance in a drained aluminium reduction cell was established by combining experiential formula and numerical simulation. A 114.5 kA drained cell was calculated by using this model. And the distribution of the electric-thermal field was obtained by the finite element analysis software. The results show that under the given process condition, the anode-cathode distance can drop to 2.75 cm, the cell system voltage drops to 3.312 V and the energy efficiency reaches 53.63%, which shows the great potential of energy saving for the drained cell. In addition, a well shaped ledge with reasonable thickness is also acquired in the investigated cell. In stable condition, the ledge is 12 cm in thickness. The research results can provide reference for design of the drained cell.
Key words: drained cell; electric-thermal balance; modeling for simulation; finite element analysis
随着异型阴极铝电解槽在工业成功应用[1]，人们加大了导流式铝电解槽[2]的研究。导流槽的结构特点是将阳极与阴极碳块做成斜坡状，并在阴极中间开排铝沟。设计合理时，电解生成的铝液可以顺着斜坡流入中间贮铝沟内，再定期被抽走。因此，阴极表面基本不存贮铝液，故不存在铝液波动问题，从而为降低极距提供了可能。然而，铝电解槽的极距不只是受到铝液波动的限制，还要受到电-热平衡的约束。为维持稳定的电解温度，极距应保持一个恰当值使电解质产生焦耳热。这部分热能通常占总输入电能的30%左右。如果能尽量降低极距而又不影响电解槽的稳定生产，将可以节省大量电能。因此，有必要对导流槽的电压平衡以及能量平衡进行深入研究。铝电解槽的电-热场研究通常采用有限元分析软件ANSYS进 行[3-5]，但其中有很多量如过电压、分解电压、电解质压降及电解反应所需能耗等需要应用经验公式来计算。本文作者采用经验公式和数值计算相结合的方法，获得导流型铝电解的电平衡和能量平衡信息，并以此为依据对导流槽的节能潜力进行分析和评估。
1 电平衡计算方法
铝电解槽的电平衡是指槽电压与各支出电压之和的平衡。电压平衡关系可由下式表示：
(1)
式中：
为槽电压，V；
为从阳极到阴极之间的电压降，V；
为阳极压降，V；
为阴极压降，V；
为母线压降，V。
通常，对铝电解槽做热平衡计算时，母线压降暂不考虑，其他压降之和则为槽体系电压。
1.1 极间压降
极间压降是指从阳极底掌到阴极(铝液)之间的压降，它由反电动势、气泡压降
和电解质
压降组成。其中反电动势是指克服电解质内所有电化学反应所需施加的电压，它又包括可逆电压
、阳极浓度差过电压
、阳极表面过电压
和阴极过电压
。因此，极间电压可表示为：
(2)
1.1.1 可逆电压
可逆电压是指Al2O3的理论分解电压，它可以通过Nernst等式计算得到：
(3)
式中：T为温度，K；Rc 为气体常数，8.31 J·mol-1·K-1；E0为标准电动势，E0=1.898-0.000 573 3T[6]，V；aAl，aCO2和aC 分别代表Al，CO2和C的活度，它们的值都为1；
为Al2O3的活度，其值可根据Dewing和Thonstard[7]提出的算式计算得到：
(4)
(5)
其中：
和
分别为氧化铝在电解质中的最大含量和实际含量(质量分数)，%。
1.1.2 阳极浓度差过电压
阳极附近的电解质所含的氧化铝浓度差会产生浓度差过电压，即阳极浓度差过电压，它通常较小，然而，它会随着电解质中的氧化铝浓度的降低而增大，并在发生阳极效应时达到最大值[8-9]。阳极浓度差过电压计算式如下[8]：
(6)
(7)
(8)
(9)
(10)
其中：J为电流密度，A·cm-2；Jcri为临界电流密度，A·cm-2；Aan为单个阳极底面积，cm-2；
为阳极效应时的氧化铝浓度(质量分数，下同)，%；Dsn为铝电解槽设计影响参数，用于补偿不同电解槽在不同氧化铝浓度而相同电流密度下的阳极效应；Rb为电解质分子质量比。
1.1.3 阳极表面过电压
它是由化学反应过慢或离子转移过慢而引起的，可以由下式确定[9]：
(11)
(12)
式中：Jr为反应限制电流密度，A·cm-2；tBk为阳极焙烧温度，℃；wLiF为LiF的质量分数，%。
1.1.4 阴极浓度过电压
阴极表面附近的铝液层的浓度差也会产生过电压。可表述如下[10]：
(13)
其中：Jcat为阴极电流密度，A·cm-2。
1.1.5 电解质压降
电解质有一定的电阻，在电流通过时会产生大量热量，并有压降。该压降与系列电流、电解质电导率、极距以及阳极尺寸有关。电解质的电导率可由电解质的成分，根据Hives等[11]提出的经验公式计算得到：
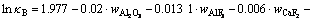
(14)
式中，κB为电解质的电导率，S·cm-1；w代表电解质中各成分的质量分数，其下标为相应成分，%；tB为电解质温度，℃。在通常情况下，当电解质成分一定时，电解质压降主要由极距决定。若仅考虑极距的影响，则电解质的压降为：
(15)
其中，I为系列电流，A； d为极距，cm；SB为阳极底掌面积，cm2。
1.1.6 阳极气泡压降
阳极气泡产生的压降有时被称为气泡过电压，尽管它属于欧姆电压，但它确有过电压的特征。依照Hyde等[12]提出的公式可计算出气泡压降：
(16)
(17)
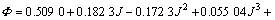
(18)
式中，db为气泡层厚度，cm；Φ为气泡在阳极底面的覆盖率。
1.2 阳极压降和阴极压降
阳极压降是指整个阳极系统压降，包括导杆压降、钢爪压降、卡具压降、爆炸焊压降、铁炭压降以及炭块压降等。阴极压降则由炭块压降和钢棒压降组成。这2部分压降对温度较敏感，温度变化会导致电导率的变化，最终影响压降。因此，这些压降需要与电解槽的热场耦合计算。而卡具、铁炭和爆炸焊的压降在ANSYS模型中无法体现出来，这2部分压降可根据实测的经验值得到。
2 能量平衡计算方法
直流电能是铝电解过程的惟一能量来源。铝电解过程是在熔融电解质中进行的，因此必须有源源不断的电能供给，来维持电解质高温熔融状态和电化学反应的进行。铝电解槽中能量的消耗主要体现在以下几个方面：电化学反应所需能量、槽体散热、出铝热损失和残极热损失。其中，槽体散热包括顶部、槽侧和槽底的散热。这部分热量需通过热场计算获得。
2.1 电化学反应所需能量
电化学反应所需电能与很多因素有关，如电流、电流效率及化学反应本身等。但它最终可表示为关于电流和电流效率的函数[13]：
(19)
其中：
为电化学反应以及加热反应物所需的总能量，J·s-1；I为系列电流，A；η为电流效率。
2.2 出铝热损失
通常出铝所带走的热量占总能量的2%~3%。其值可根据行业标准[14]给出的公式计算：
(20)
式中：c1为铝在20~660 ℃的平均比热容，J·kg-1·℃-1; c2为熔铝的平均比热容，J·kg-1·℃-1；c3为铝熔化所需比热容，J·kg-1·℃-1；t1为环境温度，℃；t2为铝的熔点，℃；t3为电解温度，℃； M为电解槽的单位时间原铝产量，kg·h-1。
2.3 残极热损失
现行铝电解必须定期更换阳极，其残极会带走部分热量，这部分热量可根据式(21)计算[14]。
(21)
其中：m为残极质量，kg；c为炭阳极比热容，J·kg-1·℃-1；t4为残极温度，℃；D为换极周期，d。
3 电-热场耦合计算模型
如前所述，阳极压降、阴极压降以及槽体散热需要借助电－热场耦合计算方法得到，常用的工具是采用ANSYS软件进行建模。由于铝电解槽的结构较为复杂，在建立计算模型时有必要进行合理简化。这些简化假设可参考文献[5]。
3.1 物理模型
导流槽结构与普通槽结构有所差别，如阴极有贮铝沟、极距很小及槽膛较浅等。因贮铝沟对热场影响很小，建模时可忽略。基于这些合理假设后，针对本文研究对象所建立的1/4槽网格化的物理模型如图1所示。
3.2 数学模型
3.2.1 控制方程
对导流槽的电场和热场进行耦合计算，需求解导电和导热微分方程。
(1) 导电微分方程：
(22)
其中：σ为材料的电导率；V为电位。
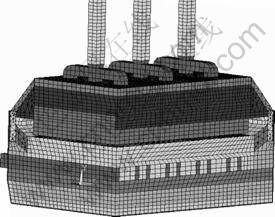
图1 导流槽网格化的物理模型
Fig.1 Model and mesh of drained cell model
(2) 导热微分方程：
(23)
其中，λ为材料的热导率，W/(m2·℃)；q为内热源单位时间内产热率，与式(22)中的电位V有关，因此，须对两式耦合求解。
3.2.2 边界条件
计算中电边界条件及部分热边界条件与文献[3]所述一致，但炉帮与电解质之间的换热系数有所不同。熔体与结壳的换热系数很测定也难以计算得到，中外文献给出的结果存在很大的差异，从200~1 600 W/(m2·℃)不等[15-16]。事实上，内侧换热系数相差700 W/(m2·℃)时，侧部换热量相差不到1%[4]。对于导流槽，因阴极上没有铝液，电解质流动受其影响会大大减小，因此换热系数会减小。本文计算中取值为文献[15-16]所给平均值的30%。
3.2.3 工艺参数
针对本文研究对象，计算中所用到的工艺参数及电解质成分(质量分数)如表1和表2所示。
表1 导流槽主要设计参数
Table 1 Design parameters of drained cell
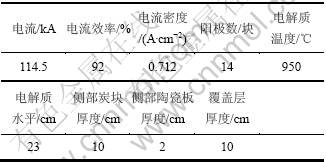
表2 电解质成分(质量分数)
Table 2 Components of electrolyte %
4 计算结果与分析
用ANSYS对所建立的模型求解时，第1次求得的解并不能直接使用，因为模型中初始炉帮厚度是人为设定的，并不是其真实值。为此，需在计算结束后，检验炉帮最外层所有节点的温度是否等于电解质初晶点温度。若不相等，则相应移动其位置再计算1次，直到全部达到设定的温度误差为止。经多次计算和调整，最终得到稳态的电-热场计算结果。其中温度场如图2所示。导流槽各项参数如表3所示。由表3可知，导流槽的极距只有2.75 cm，这远比普通槽的要小。其原因是槽体采用陶瓷纤维板加强保温使得散热量减少，从而总热支出减小，因此，电解槽输入能量就可以相应减小，故极距和槽电压可降低。极距能降至如此之低，其根本原因还是导流槽的阴极上不贮存铝液，消除了铝液波动，保证了电解槽工作的稳定性。这也正是导流槽的优越性所在。
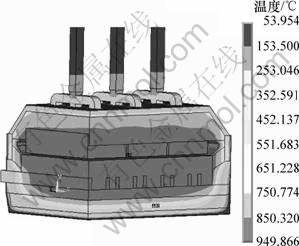
图2 导流槽热场图
Fig.2 Temperature field distribution in cell
表3 导流槽主要参数计算结果
Table 3 Main results of drained cell
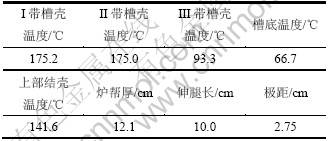
从表3还可看出：Ⅰ带(焙体区域)槽壳平均温度和Ⅱ带(阴极区域)槽壳平均温度基本一致。在通常情况下，Ⅰ带平均温度比Ⅱ带的更高，在这里是因为Ⅰ带内衬加了一层2 cm的陶瓷纤维板，而Ⅱ带没有加强保温，故Ⅰ带保温效果更好，从而外侧温度也会降低。另外，导流槽的炉帮平均厚度为12.1 cm。这一厚度比较理想，能起到保护内衬的作用。
为更清楚地了解导流槽的能量收支平衡，表4和表5列出了计算所得的能量平衡数据。
表4 导流槽内电压分配
Table 4 Voltage list of drained cell
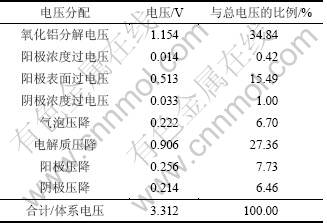
表5 导流槽能量支出表
Table 5 Energy expenditure of drained cell
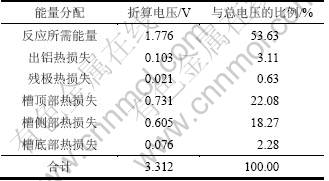
从表4可知：稳态时导流槽的体系电压为3.312 V，远低于普通槽的体系电压。其主要原因是电解质压降小，仅为0.906 V，其节电效果也主要由此体现。从表5可以看出：导流槽中反应所需能量占总能量的53.63%，远超过普通槽所需能量，说明导流槽的能量利用率有很大提高。槽体散热损失方面，顶部散热最多，占总能量的22.08%；侧部散热次之，占18.27%，这2部分是铝电解槽消耗的主要电能。以114.5 kA系列普通槽为例，实测的侧部和顶部散热损失占总能量的50.4%。可见导流槽约减少了10%的热损失。其原因主要是：(1) 侧部加强保温，使散热减少；(2) 顶部覆盖层加厚有利于顶部保温。
5 结论
(1) 采用经验公式计算和数值计算相结合的方法建立导流槽电平衡和能量平衡计算模型能方便地获得电-热场分布和电-热平衡的全部信息。
(2) 导流槽通过加强顶部和侧部的保温可以有效地降低极距和槽电压。
(3) 114.5 kA导流槽体系电压可降至3.312 V，与现有普通槽(体系电压约为4.1 V)相比可降低19.2%，因而具有巨大的节能潜力，值得在工业中推广。
参考文献：
[1] 冯乃详. 低能耗新型阴极铝电解槽：中国, 200710010523[P]. 2007-05-23.
FENG Nai-xiang. Low energy consumption aluminum reduction cell with novel cathodes: China, 200710010523[P]. 2007-05-23.
[2] 周乃君, 李劼. 一种导流TiB2涂层阴极铝电解槽:中国，200410023392.X[P]. 2004-07-06.
ZHOU Nai-jun, LI Jie. One type of aluminium reduction cell with drained cathode coated with TiB2 layer: China, 200410023392. X[P]. 2004-07-06.
[3] 罗海岩, 陆继东, 黄来, 等. 铝电解槽三维电热场的ANSYS分析[J]. 华中科技大学学报: 自然科学版, 2002, 30(7): 4-6.
LUO Hai-yan, LU Ji-dong, HUANG Lai, et al. Aluminum reduction cell’s three dimension electro-thermal field analysis through ANSYS[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2002, 30(7): 4-6.
[4] 马素红. 基于ANSYS的大型预焙铝电解槽热电场的仿真[D]. 北京: 北方工业大学自动化系, 2007: 19-22.
MA Su-hong. The simulation of the thermal-electric field of large prebaked aluminum reduction cell based on ANSYS[M]. Beijing: North Industry University. Department of Automation, 2007: 19-22.
[5] 周乃君, 崔大光, 周正明等.铝电解槽电热场1/4槽模型有限元解析方法及应用[J]. 轻金属, 2006(11): 37-40.
ZHOU Nai-jun, CHUI Da-guang, ZHOU Zheng-ming, et al. Numerical simulation and application on thermal-electric field of a quarter of aluminum reduction cell[J]. Light Metals, 2006(11): 37-40.
[6] Haupin W, Kvande H. Thermodynamics of electrochemical reduction of alumina[C]//Light Metals, Warrendale: Minerals Metals and Materials Society, 2000: 379-384.
[7] Dewing E W, Thonstad J. Activities in the system cryolite-alumina[J]. Metallurgical and Material Transaction B, 1997, 28B: 1089-1093.
[8] Haupin W. Interpreting the components of cell voltage[C]//Light Metal. Warrendale: Minerals, Metal and Materials Society, 1998: 531-537.
[9] 邱竹贤. 预焙槽炼铝[M]. 北京: 冶金工业出版社, 2005: 5-15.
QIU Zhu-xian. Aluminium smelting by pre-baked aluminium pot[M]. Beijing: Metallurgy Industry Press, 2005: 5-15.
[10] Grjotheim K, Kvande H. Introduction to aluminium electrolysis: Understanding the Hall-Héroult process[M]. 2nd ed. Düsseldorf: Aluminium-Verlag, 1993: 144.
[11] Hives J, Thonstad J, Sterten A, et al. Electrical conductivity of molten cryolite based mixtures obtained with a tube-type cell made of pyrolytic boron nitride[J]. Metallurgical and Materials Transaction B, 1996, 27(2): 255-261.
[12] Hyde T M, Welch B J. The gas under anodes in aluminium smelting cells part I: Measuring and modeling bubble resistance under horizontally oriented electrodes[C]// Light Metals. Warrendals: Minerals, Metal and Materials Society, 1997: 333-340.
[13] ?stb? N P. Evolution of alpha phase alumina in agglomerates upon addition to cryolite melts[D]. Trondheim: Norwegian University of Science and Technology. School of Energy and Process Engineering, 2002: 1-20.
[14] YS-T 481—2005, 铝电解槽能量平衡测试与计算方法五点进电和六点进电预焙阳极铝电解槽[S].
YS-T 481—2005, Aluminum pot test and calculating method for energy balance in five and six electricity entrance points pre-baked anode aluminum pot[S].
[15] 冯乃祥, 梁芳慧. 160 kA大型预焙铝阳极铝电解槽温度场及槽帮与熔体间换热系数的计算[J]. 有色金属(冶炼部分), 1999(3): 18-22.
FENG Nai-xiang, LIANG Fang-hui. Thermal field and the heat transfer coefficient between the ledge and the bath in 160 kA large type aluminum reduction cells[J]. Nonferrous Metals (Extractive Metallurgy), 1999(3): 18-22.
[16] Taylor M P, Zhang W D, Wills V, et al. A dynamic model for the energy balance of an electrolysis cell[J]. Trans IChemE, 1996, 74(A): 913-933.
(编辑 赵俊)
收稿日期：2010-12-26；修回日期：2011-04-10
基金项目：湖南省科技计划重点项目(2009GK2009)
通信作者：周乃君(1963-)，男，湖南常德人，博士，教授，从事工业节能研究；电话：0731-88876554；E-mail：njzhou@csu.edu.cn
