J. Cent. South Univ. Technol. (2009) 16: 1001-1005
DOI: 10.1007/s11771-009-0166-4
Stability analysis of shallow tunnels subjected to seepage with
strength reduction theory
YANG Xiao-li (杨小礼), HUANG Fu (黄 阜)
(School of Civil and Architectural Engineering, Central South University, Changsha 410075, China)
Abstract: Based on strength reduction theory, the stability numbers of shallow tunnels were investigated within the framework of upper and lower bound theorems of limit analysis. Stability solutions taking into account of water seepage were presented and compared with those without considering seepage. The comparisons indicate that the maximum difference does not exceed 3.7%, which proves the present method credible. The results show that stability numbers of shallow tunnels considering seepage are much less than those without considering seepage, and that the difference of stability numbers between considering seepage and without considering seepage increase with increasing the depth ratio. The stability numbers decrease with increasing permeability coefficient and groundwater depth. Seepage has significant effects on the stability numbers of shallow tunnels.
Key words: strength reduction theory; seepage; permeability coefficient; stability numbers
1 Introduction
Limit analysis, characteristics and limit equilibrium methods are the traditional methods for determining the stability numbers of shallow tunnels. These methods are commonly applied to tunnel stability analysis since they were proposed for their simplicity and exactness. However, each of these methods also has its own deficiencies. For example, the relationship of soil between stress and strain is ignored, and the hypothetical critical failure surface should be set at the beginning of analysis[1-4]. Strength reduction theory not only overcomes these disadvantages but also takes into account of the nonlinear constitutive relation for soil. This method can simulate the deformation process in stability analysis of earth structures such as slope, foundation bearing capacity and earth pressure of retaining walls, and it is suitable for any complex boundary conditions. Consequently, the numerical results using the strength reduction theory are more accuracy. The strength reduction theory was applied to studying stability problems of earth structures such as soil slope and retaining walls[5-7]. It is obvious that strength reduction theory is widely used in slope stability analysis and developed as a mature theory. However, there has been no reasonable and reliable criterion to assess the stability of tunnels for a long period. The factor of safety and failure surface for tunnels cannot be calculated simply based on the stress, displacement, and plastic region by the traditional finite element method. As a result, strength reduction theory begins to apply to tunnel stability analysis.
The aforementioned research for tunnel stability analysis by strength reduction theory does not take into account of the effect of underground water seepage. However, underground water is one of the environmental factors for rock masses, and stress field and displacement field around the underground opening are constantly affected by seepage field. For tunnels deeply buried in water-rich rock masses or bearing high hydraulic pressure, the effect of seepage field on surrounding stress and displacement fields will reach a point that cannot be ignored. Taking into account of seepage, LEE and NAM[8] calculated the upper bound solution of the face stability for a circular tunnel driven through sandy soil by limit analysis. Consequently, reasonable design concepts applicable to the design of tunnel lining and to the evaluation of the support pressure required for maintaining the stability of the tunnel face were suggested for underwater tunnels. A proposed model to predict the disturbance of hydraulic conductivity caused by excavating around the Syueshan tunnel in fractured rocks by LIN and LEE[9]. The closure of fractures was assumed to be the sole factor that caused hydraulic conductivity changes, and a hyperbolic relationship between normal stress and closure was introduced instead of using a linear relation in their research.The instability of surrounding rock around tunnel caused by underground water seepage is one of the significant factors among various influencing factors for tunnel stability analysis, and the documents considering seepage effect by strength reduction theory was rare. Taking account of seepage effect, the strength reduction theory was applied to calculating the factor of stability for tunnel in this work. By comparing the difference of factors of stability for tunnel between taking account of seepage and without taking account of seepage, the influence of seepage effect for surrounding rock around tunnel was investigated.
2 Stability number by limit analysis
The construction of a shallow tunnel in soils is often excavated by shield machine. The soils are removed from the tunnel face either by hand or by cutter, and the tunnel stability is controlled by the machine with compressed air, bentonite or clay slurry. Under these conditions, it is possible to idealize the construction of tunnel[10]. According to a series of experiment results, an equation was used to calculate the stability numbers of shallow tunnels in cohesive soil. The equation is as follows:
N=[σs-σt+γ(C+D/2)]/Cu (1)
where C is the tunnel depth, D is the tunnel diameter, σs is the uniform pressure acting on the soil surface, σt is the uniform fluid pressure or shoring acting on the tunnel face, γ is the unit weight, and Cu is the undrained shear strength. In the following analysis, it is assumed that Cu is constant with depth varying, although in practice Cu increases with increasing depth for the reason of the site history. The simplified mechanical model of the shallow tunnel is illustrated in Fig.1, where H is the distance from the groundwater level to the tunnel crown.
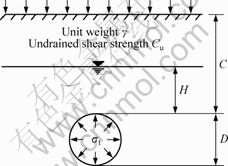
Fig.1 Plane strain unlined circular tunnel
Stability solutions can be obtained using the upper bound theorem and lower bound theorem of plastic limit analysis theory. The lower bound theorem states that if any stress field supporting the loads can be found, and is everywhere in equilibrium without yield being exceeded, then the loads will be lower than those for collapse. The upper bound theorem states that if a work calculation is performed for a kinematically admissible collapse mechanism, then the loads thus deduced will be higher than those for collapse. DAVIS et al[11] argued that, the stability number was a approximate function of C/D and γD/Cu, thus the problem could be regarded as finding the value of (σs-σt)/Cu in its limit once the values of parameters C/D and γD/Cu were fixed. Consequently, lower and upper bound solutions for values of γD/Cu from 1 to 2 were calculated respectively, and then stability numbers were computed.
3 Stability number by strength reduction
If the model is unstable, the finite element strength reduction calculation will not converge in static computation. Based on the technique, when the soil reaches limit equilibrium state the element static computation will undergo the process from converging to non-converging through reducing the strength parameter of soil, and the reduction coefficient is the factor of safety for shallow tunnel at the time. Herein, the cohesion of soil is chosen for the reduction strength parameter, and the reduction coefficient is defined as:
Cn=C0/Fn (2)
where Fn is the reduction coefficient, C0 is the actual cohesion of soil, and Cn represents a series of trial cohesions that have been reduced. Then, simulations are run for a series of trial cohesions until the tunnel reaches limit equilibrium state, and the corresponding reduction coefficient is the minimum factor of safety for shallow tunnel at the time. The detailed process is as follows: Fn denotes a sequence of numbers from F1 to Fn, so Cn corresponding to Fn also denotes a sequence of numbers that are represented as, C1=C0/F1, C2=C0/F2, …, Cn=C0/Fn. Then, C1, C2, …, Cn are tested. If the maximum unbalanced force is less than 1×10-3 when Cn-1 is tested, and the maximum unbalanced force is larger than 1×10-3 when Cn is tested, the limit equilibrium state will be reached, and Cn will be the critical value of cohesion. According to the factor of safety Fs as defined by Bishop, factor of safety is the ratio of the actual soil shear strength to the critical shear strength when limit equilibrium state is reached. The factor of safety Fs is given by
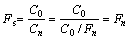(3)
The strength reduction technique based on finite element method has been applied mostly to slope stability, which illustrates failure mechanism involving deforming wedges. The results using the technique agree well with the slice solutions of limit equilibrium, which shows the effectiveness[12-14].
However, how to judge whether the simulation reaches limit equilibrium is crucial for calculating the factor of safety. In this work the limit equilibrium state is determined by the convergence of finite element calculation. If the distinction of unbalanced force cannot meet the required convergent condition, the soil will reach the limit equilibrium state under the given reduction coefficient.
4 Results of stability number with seepage
4.1 Stability number for saturated soils
The computer code is the explicit finite difference program, and it is possible to perform the seepage as well as the mechanical analysis. In order to stimulate the percolation characteristic of surrounding rock around tunnel under the condition of full saturation, the boundary condition is set as follows. The groundwater level is located at the top of the grid, and the pore pressure is fixed to be zero at grid points along the top of the grid. Then the saturation is set to 1 at the same position. Thus, the fully saturated condition is established. The excavating boundary is free draining boundary and the pore pressure around this boundary is fixed at zero. As a result, the groundwater infiltrates into the tunnel under the effect of pore pressures. The left, right and bottom boundaries of the grid are set to be impermeable, since the influence of seepage on the stability of surrounding rock around tunnel in the region is extremely small. Besides, the initial pore pressure is assumed as hydrostatic pressure and distributed along depth according to linear law. The whole simulating process is divided into two steps. Firstly, the flow and mechanical calculation is turned off, and the fully saturated soil is solved to mechanical equilibrium. Then tunnel is excavated. Secondly, turn on the flow and mechanical calculation, and solve the coupled fluid- mechanical problem until the convergence of finite element calculation is reached.
Without considering the effect of underground water seepage, when γD/Cu=2, friction angle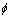
=0?, C/D varying from 1 to 4, the stability numbers of shallow tunnel are calculated by strength reduction theory. By comparing with the solutions of DAVIS et al[11] using limit analysis, it can be seen that, whether it is upper bound solution or lower bound solution, the maximum difference between strength reduction and limit analysis solution of stability numbers for shallow tunnel will not exceed 3.7%. Therefore, the stability numbers calculated by strength reduction is credible. When γD/Cu=2, friction angle 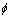=0?, C/D varying from 1 to 4 and taking account of underground water seepage, the simulations are run for different values of (σs-σt)/Cu by using strength reduction theory until the factor of safety reaches an approximate value that is the sign of limit equilibrium state. Then the stability numbers of shallow tunnel, with effect of seepage taken into account, can be computed by substituting the aforementioned values into Eq.(1). As shown in Fig.2, the stability numbers of shallow tunnel considering seepage are much less than those without considering seepage, and the difference of stability numbers under these two conditions increases with the increase of C/D. When C/D=1, the stability numbers of shallow tunnel considering the seepage are 9.6% less than those without considering seepage. However, when C/D=4, the stability numbers of shallow tunnel with considering of seepage are 41.5% less than that without considering seepage. As a consequence, with the increase of tunnel depth and the decrease of tunnel radius, the effect of seepage on surrounding rock around tunnel increases.
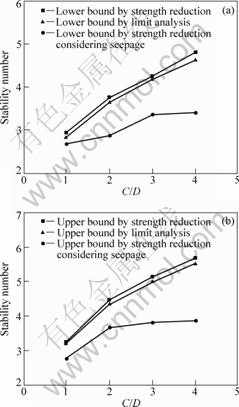
Fig.2 Comparison of stability numbers considering seepage or without considering seepage: (a) Lower bound solutions; (b) Upper bound solutions
4.2 Stability numbers of shallow tunnel with permeability
Based on Biot consolidation theory the coupled fluid-solid theorem is used to calculate the stability numbers, and the corresponding governing differential equation can be described by Darcy’s law. For an anisotropic porous medium, Darcy’s law can be reduced to:
qi=-k?p/?xj (4)
where qi is the specific discharge which is the same meaning of average seepage velocity, k is the permeability coefficient, ?p/?xj is hydraulic gradient, and p is pore water pressure. Eq.(4) shows that the permeability coefficient k is the direct proportion coefficient between seepage velocity and hydraulic gradient in the state of laminar flow, and that its dimension is the same as velocity. When the hydraulic gradient is given, the permeability coefficient increases with increasing the velocity. The seepage velocity reflects the permeability of soil, so the permeability coefficient can be used as a criterion to assess the permeability of soil. The permeability coefficient of soil is large, and the water in soil is easy to flow. The contour diagrams of hydraulic head with different level depth ratios H/D under the same value of C/D is given by
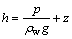(5)
where h is the hydraulic head, g is the weight acceleration, ρw is the density of water, and z is the vertical distance from a certain datum. For the purpose of studying the effect of permeability coefficient on stability numbers of shallow tunnel, the stability numbers are computed when γD/Cu=2, friction angle 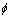=0?, per- meability coefficient k=1×10-4, 1×10-5 and 1×10-6, and C/D varying from 1 to 4, respectively. As shown in Fig.3, with the increase of permeability coefficient, the stability numbers is decreasing. This phenomenon may be reasonably explained as follows. As the hydraulic gradient being a certain value, the permeability coefficient of tunnel surrounding rock increases with the increase of underground water seepage. The influence of secondary stress and displacement field on primary stress and displacement field is aggravated by the seepage effect. Consequently, the stability numbers are reduced
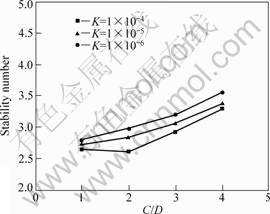
Fig.3 Relationship between stability number and permeability coefficient
and tunnel surrounding rock becomes unstable.
4.3 Stability numbers of shallow tunnel with groundwater level depth ratio H/D
All the aforementioned researches of tunnel stability analysis are for the fully saturated soil. However, plenty of tunnels in practice are not located in fully saturated soil. For instance, the groundwater level will vary when the rainy season comes in seasonal rain area. Therefore, it is important to take account of the variation of the groundwater level in stability analysis of shallow tunnel. In order to investigate the effect of groundwater level on stability numbers for shallow tunnel when the permeability coefficient is the same, groundwater level depth ratio H/D is applied to describing the variation of groundwater level in this work. Similar to the process above, the stability numbers of shallow tunnel are computed by strength reduction theory when γD/Cu=2, friction angle=0?, C/D varying from 1 to 4, and H/D varying from 1 to 3, respectively. As shown in Fig.4, when C/D is the same, the stability numbers decrease with increasing H/D.
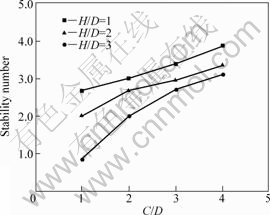
Fig.4 Relationship between stability number and level depth ratio
It can be seen from Fig.5 that the distribution of hydraulic head becomes dense with increasing H/D. Fig.5 demonstrates that when H/D=1, the hydraulic head varies 15.0 m from the tunnel face to upper boundary and 17.5 m from the tunnel face to upper boundary for the case H/D=2. Besides, the variation of hydraulic head between tunnel face and upper boundary is 18.5 m at H/D=3. This result indicates that when groundwater level depth ratio H/D is larger, the head difference of tunnel between the internal and the external is larger. The diffusion velocity of groundwater in soil is determined by hydraulic head. As a result, the diffusion velocity of groundwater is faster when H/D is larger, which causes the decrease of tunnel stability numbers.
Fig.5 Contour diagrams of hydraulic head (m) with different level depth ratios: (a) H/D=1; (b) H/D=2; (c) H/D=3
5 Conclusions
(1) Based on strength reduction theory, taking account of groundwater seepage, the stability numbers of shallow tunnel are calculated. By comparing with the solution of upper and lower bound by limit analysis without considering seepage, it can be concluded that the stability numbers of shallow tunnel considering seepage are much less than those without considering seepage, and that the difference of stability numbers between considering seepage and without considering seepage increases with the increase of C/D.
(2) Stability numbers of shallow tunnel for different permeability coefficients are computed by strength reduction theory. The results show that, when the hydraulic gradient is a certain value, the diffusion velocity of groundwater increases with the increase of permeability coefficient. Consequently, the seepage effect on the stability of tunnel surrounding rock is aggravated, which causes the decrease of tunnel stability numbers.
(3) By simulating the variation of groundwater level depth ratio H/D, the stability numbers of shallow tunnel for imperfect saturated are calculated. The calculated results indicate that when groundwater level depth ratio H/D is larger, the hydraulic head difference of tunnel between internal and external is larger. Still, when permeability coefficient is a certain value the stability numbers decrease with the increase of H/D.
References
[1] ZHAO Ming-hua, LIU Jian-hua, LIU Dai-quan, WANG You. Force analysis of pile foundation in rock slope based on upper-bound theorem of limit[J]. Journal of Central South University of Technology, 2008, 15(3): 404-410.
[2] YANG Xiao-li, LI Liang, YIN Jian-hua. Stability analysis of rock slopes with a modified Hoek-Brown failure criterion[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2004, 28(2): 181-190.
[3] YANG Xiao-li, LI Liang, YIN Jian-hua. Seismic and static stability analysis for rock slopes by a kinematical approach[J]. Geotechnique, 2004, 54(8): 543-549.
[4] YANG Xiao-li, YIN Jian-hua. Slope stability analysis with nonlinear failure criterion[J]. Journal of Engineering Mechanics, 2004, 130(3): 267-273.
[5] DAWSON E M, KOTH W H, DRESCHER A. Slope stability analysis by strength reduction[J]. Geotechnique, 1999, 49(6): 835-840.
[6] CHENG Y M, LANSIVAARA T, WEI W B. Two-dimensional slope stability analysis by limit equilibrium and strength reduction methods[J]. Computers and Geotechnics, 2007, 34 (1): 137-150.
[7] KANG K W, KIM H S, KIM M S, KIM J K. Strength reduction behavior of honeycomb sandwich structure subjected to low-velocity impact[J]. Materials Science and Engineering, 2008, 483/484(1/2): 333-335.
[8] LEE I M, NAM S W. The study of seepage forces acting on the tunnel lining and tunnel face in shallow tunnels[J]. Tunnelling and Underground Space Technology, 2001, 16(1): 31-40.
[9] LIN H I, LEE C H. An approach to assessing the hydraulic conductivity disturbance in fractured rocks around the Syueshan tunnel, Taiwan[J]. Tunnelling and Underground Space Technology, 2009, 24(4): 222-230.
[10] NAKAMURA H, KUBOTA T, FURUKAWA M, NAKAO T. Unified construction of running track tunnel and crossover tunnel for subway by rectangular shape double track cross-section shield machine[J]. Tunnelling and Underground Space Technology, 2003, 18(2/3): 253-262.
[11] DAVIS E H, DUNN M J, MAIR R J, SENEVIRATNE H N. Stability of shallow tunnels and underground openings in cohesive material[J]. Geotechnique, 1980, 30 (4): 397-416.
[12] CHEN Jing-xi, KE Peng-zhen, ZHANG Guang. Slope stability analysis by strength reduction elasto-plastic FEM[J]. Key Engineering Materials, 2007, 345/346(1): 625-628.
[13] LI R Q, YU Y Z, DENG L J, LI G X. Stability analysis of unsaturated soil slope by 3D strength reduction finite element method[J]. Geotechnical Special Publication, 2006, 148: 62-69.
[14] DAWSON E M, NESARAJAH S, ROTH W H. 3D Geotechnical stability analysis by strength reduction[J]. ASCE Special Publication, 2000, 101: 99-113.
(Edited by YANG You-ping)
Foundation item: Project(200550) supported by the Foundation for the Author of National Excellent Doctoral Dissertation of China; Project(09JJ1008) supported by Hunan Provincial Natural Science Foundation of China; Project(200631878557) supported by West Traffic of Science and Technology of China
Received date: 2009–03–02; Accepted date: 2009–06–06
Corresponding author: YANG Xiao-li, Professor; Tel: +86-731-82656248; E-mail: yxnc@yahoo.com.cn
