一种基于自适应输入—输出线性化的
无刷直流电机参数辨识方法
揭贵生, 马伟明
(海军工程大学 电力电子技术研究所, 湖北 武汉, 430033)
摘要: 对基于理想换相的永磁无刷直流电机, 在给出其单相等效模型的基础上, 运用基于自适应输入—输出线性化(AIOL) 方法, 设计了适用于无刷直流电机的参数辨识与控制的电流控制器, 来提高驱动控制系统对电机参数的自适应能力; 此外, 对辨识方法进行相应的改进。 研究和仿真分析结果表明: AIOL方法不要求各状态量解耦, 参考模型中也不包含估计状态量, 因而自适应律的导出较简单, 并且使参数辨识与电机控制在一个框架内得到解决, 更适合电机的运行控制; 基于AIOL方法的改进参数辨识算法消除了待辨识参数变化互相耦合、 相互抵消的负面影响, 能够准确、 稳定地估计电机参数, 且系统的响应性能较好, 易于工程实现。
关键词: 永磁无刷直流电机; 自适应输入—输出线性化; 参数辨识
中图分类号:TM33 文献标识码:A 文章编号: 1672-7207(2005)06-1069-05
A parameter identification method of brushless DC motor
based on adaptive input-output linearization
JIE Gui-sheng, MA Wei-ming
(Institute of Power and Electronics Technology, Naval University of Engineering, Wuhan 430033, China)
Abstract: Equivalent single phase model of brushless DC motor (BLDCM) is deduced assuming it can commutate ideally. In order to improve the adaptive capability of the driving control system when the motor parameters vary, the current controller which is suitable for the control and parameter identification of BLDCM is designed based on adaptive input-output linearization method. The parameter identification method was improved. The research and simulation results show that the adaptive rule can be deduced easily with the AIOL method because it doesnt require the state quantities’ discoupling and the estimated state quantities needn’t be included in the reference model ; at the same time, the method can make the parameter estimation and motor control solved in the same frame, so it is more suitable for the motor operation control. The improved parameter identification algorithm based on adaptive input-output linearization can estimate the motor parameters exactly and stably with good system response as it eliminates the parameters’ negative influences of mutually counteracting.
Key words: brushless DC motor; adaptive input-output linearization; parameter identification
永磁无刷直流电机(BLDCM)既具有交流电机结构简单、 运行可靠、 维护方便的特性, 又兼有直流电机控制简单的优点, 而且具有比正弦波永磁同步电机更大的转矩/电流比, 因而得到较广泛的应用[1, 2]。 然而, BLDCM在运行过程中其电机参数难免会发生变化(特别是永磁磁链和电感均因饱和而减小), 使得电机额定工作点也会相应变化。 对于控制系统, 确切的电机参数可用于判断电机的运行状态, 当采用一些附加控制方法时(如换相转矩脉动补偿), 需要知道确切的电机参数[4, 5]; 此外, 即使采用PID控制, 控制器参数也要根据系统模型和参数进行合理选择和调整, 故电机参数的辨识与自适应问题显得很重要。 对此, 很多研究者运用模型参考自适应(MRAS)方法、 基于线性矩阵不等式(LMI)的H2/H∞参数鲁棒控制方法、 人工神经网络(ANN)方法等对永磁电机参数辨识和自适应问题进行了研究, 结果表明: MRAS方法要求电机各状态量解耦, 并且不能同时估计电机的电阻、 电感和磁链参数; 而采用H2/H∞的参数鲁棒控制方法和ANN方法时需进行大量的矩阵运算或梯度和加权运算, 对CPU的要求高, 工程实现上难度较大[6-11]。 基于上述情况, 本文作者针对理想磁通分布的导通型三相BLDCM, 在忽略换相影响的情况下, 运用AIOL方法, 在线辨识电机参数, 并针对参数变化互相耦合、 抵消的不利情况, 对辨识算法进行改进, 以此来提高控制系统对电机参数的自适应能力。
1 理想BLDCM的单相等效模型
对于理想磁通分布的梯形波三相BLDCM, 在忽略凸极效应的影响(因为BLDCM多为转子表面磁体结构, 因而凸极效应很小), 当采用三相六状态换相控制方式时, 在理想换相情况下(忽略因电枢电感带来的续流问题), 各相电流在1个周期内为240°方波, 任何时候只有两相导通, 且两相电流和反电动势大小分别相等、 极性相反, 因而, 电机可等效为电阻、 电感和永磁磁链均为各相2倍的单相永磁电机, 因而有如下电压、 转矩和转矩-运动方程:

其中: Rs, Ls, M和Ke分别为电机各相电阻、 自感、 各相之间互感和永磁磁链; R, L和KE分别为等效的单相电阻、 电感和永磁磁链(R=2Rs, L=2(Ls-M), KE=2Ke); U和i分别为等效单相电机的供电电压和电流(即任何时候导通两相间的线电压和线电流); pn, ωe和ωr分别为电机极对数、 电磁转速和机械转速; Te, Tl和B分别为电机电磁转矩、 负载转矩和粘滞阻力系数。
由上述方程可见, 在理想情况下, 只要换相准确, 则BLDCM的电磁转矩与等效单相电机的供电电流成正比, 因而, 通过控制其供电电压就可以很好地控制电机的电磁转矩和转速。 典型的BLDCM双闭环调速系统原理如图1所示, 速度调节器根据转速偏差产生指令电流, 电流调节器根据电流偏差产生供电电压U, 根据三路霍尔位置信号进行换相, 实现自同步, 从而产生恒定的电磁转矩。

图 1 典型BLDCM调速系统原理框图
Fig. 1 The block diagram of the typical speed control system of BLDCM
2 基于AIOL的BLDCM参数在线估计
2.1 估计原理
式(1)可改写为如下参数形式的状态方程:
i=θT1φ1+θ2φ2。(4)
其中: θ1和θ2为系数参数; φ1和φ2为状态量, 且有: θ1=[-R/L -Kepn/L]T, φ1=[i ωr]T, θ2=1/L, φ2=U。 待估计参数为θ1和θ2, 其估计值记为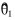 和
和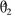 , 且有:
, 且有:  ,
, 。
。
由式(4), 输出控制量U可表示为:
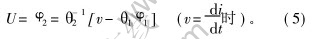
由式(5)可知, θ2为大于0的正数, 并且式(4)和(5)所表示系统的相对阶为1, 因此, 式(4)是可以输入-输出线性化的, 参数估计可用基于自适应输入-输出线性化辨识方法, 并且对于本系统, 只要满足相对阶小于或等于1的条件, 稳定性同样能得到保证。 基于AIOL的辨识方法与模型参考自适应(MRAS)方法的不同之处在于, 不要求状态量解耦, 只用估计参数替代系统未知的真实参数构成参考模型, 参考模型中并不包含估计状态量, 使得由李亚普诺夫函数导出自适应律较简单, 并且控制量直接根据参考模型得出, 使参数辨识与电机控制在一个框架内得到解决, 因而更适合电机的运行控制[12, 13]。
由AIOL方法, 参考模型方程可定义为:

其中: e=i-iref; g>0, 为常数。 定义:

由以上2式可得:

因此, 有:

定义目标李亚普诺夫函数包含电流和参数误差, 即:

那么:
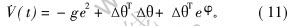
为保证在任何时候都有[AKV·](t)≤0, 使得辨识算法的渐近稳定性得到满足, 取:

则 。 若假定电机参数θ为慢变参数, 则有:
。 若假定电机参数θ为慢变参数, 则有:

因此, 由式(5), 辨识期间电流跟踪控制方程为:

综上所述, 辨识原理及过程如图2所示。 BLDCM真正电流i与转速调节器输出的电流指令值iref相减得到电流误差, 由式(13)所示的辨识算法不断调整参考模型电机参数, 并根据参考模型由电流指令值iref得到电机控制电压U来控制电机电流, 这样通过不断辨识调整, 使得当电流误差越小时, 参考模型参数与真正电机参数间的偏差也越小, 最终使参考模型电机参数逐渐收敛于BLDCM真正参数。

图 2 基于AIOL的BLDCM参数辨识原理框图
Fig. 2 The block diagram of the parameter identification method based on AIOL
2.2 估计算法的缺陷
由式(13)可知, 估计算法能准确估计BLDCM参数的前提是: 当电机参数变化时, 电流误差也能发生相应变化。 但实际上, 对于BLDCM, 在某些情况下, 这个前提是不存在的。 例如, 假定L和U不变, 且电机电磁暂态比机械动态快得多, 则ωr可认为是不变的。 当R和KE分别变化为: R=R0+ΔR, KE=KE0+ΔKE(R0和KE0分别为参数发生变化前电机等效电阻和永磁磁链初始值), 由式(4), 在参数变化前、 后, 有:
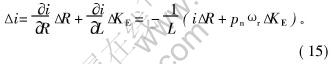
可见: 无论对于BLDCM, 还是对于其参考模型, 在参数发生变化或参数估计调整前、 后, 如果ΔR和ΔKE符号相反(即R与KE的变化趋势相反, 实际运行时通常是R增大, KE减小), 且ΔR和ΔKE在一定范围内取值时, 由式(15)可知, 它们对电流响应式(4)的影响是互相抵消的, 有可能使得电流变化趋势为0而电流误差e不变。 由(13)可知, 如果同时估计电机的R和KE, 则估计参数无法作相应调整, 因而有可能导致电机参数估计值与真实值差别较大。
针对采用图2所示辨识算法的BLDCM驱动控制系统, 对上述情况进行验证仿真分析, 仿真参数及工况如下:
电机参数: R=24 mΩ, L=300 μH, KE=18.5 mWb, pn=6, 额定转速ωrN=400 rad/s, 直流侧供电电压Vd=48 V, 转动惯量J=5 g·m2, Tl=7.8 N·m, B=0; 仿真工况为ωref=200 rad/s, 在0.2 s时转速稳定, 将电机参数变为R=48 mΩ, 而辨识器设定参数初始值仍为原电机参数, 取g=8000, 0.2 s辨识器投入使用, 同时辨识R, KE和L。
图3所示为系统的电流、 转速、 电流误差响应曲线及 的辨识及辨识误差曲线。 可见, 在辨识稳定后, 虽然电流误差为0, 电机电流与转速也已稳定, 但是
的辨识及辨识误差曲线。 可见, 在辨识稳定后, 虽然电流误差为0, 电机电流与转速也已稳定, 但是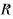 明显偏大,
明显偏大,  明显偏小。 因此, 基于通用AIOL方法同时辨识电机的R和KE是不可取的。
明显偏小。 因此, 基于通用AIOL方法同时辨识电机的R和KE是不可取的。
2.3 BLDCM改进的基于AIOL的估计策略
当把R当作已知量时(因为R的在线测量很容易实现), 就消除了在辨识时R与KE的变化互相耦合、 抵消的负面影响, 在R可测的前提下可以对KE和L较准确地辨识。 因此, 对θ和φ做如下修改:
θ=[1/L -KEpn]T, φ=[-Ri+U ωr],
θ3=1/L, θ4=-KEpn/L, φ3=Ri+U, φ4=ωr。

图 3 当电机等效电阻变大时系统辨识响应曲线
Fig. 3 The curves of the system identification response when the motor equivalent
resistance increase abruptly
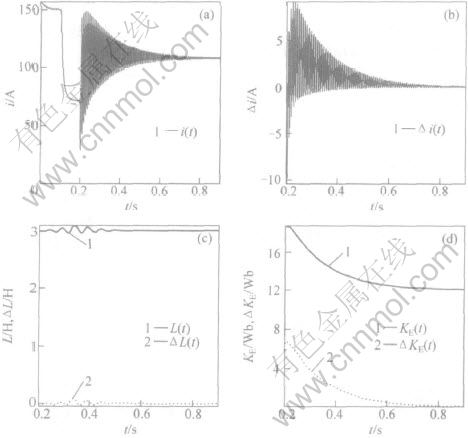
图 4 改进的基于AIOL系统辨识响应曲线
Fig. 4 The curves of the system identification response of the improved identification
method based on AIOL
显然, 辨识原理仍然如式(6)~(14)所示, 但辨识期间电流跟踪控制方程相应为:
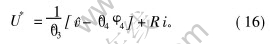
在与图3同样的仿真工况下(电机R和L不变, 0.2 s时电机参数变为KE=12 mWb), 但辨识器将R视为已知, 只同时辨识KE和L。 图4所示为系统的辨识响应曲线。 可见, 修改辨识算法能对电机KE和L的变化能准确跟踪, 并且收敛性能得到保证。
3 结 论
对基于理想换相的BLDCM, 以其单相等效模型作为研究对象, 运用基于自适应输入-输出线性化(AIOL)的参数辨识方法, 来提高控制系统对电机参数的自适应能力。 研究和仿真分析表明: 基于AIOL方法在线辨识电机参数, 必须根据实际情况对算法进行相应修改, 消除待辨识参数变化互相耦合、 抵消的负面影响后才能准确、 稳定地估计电机参数, 且系统的响应性能较好, 自适应律的导出较简单, 易于工程实现。
参考文献:
[1]张琛. 直流无刷电动机原理及应用[M]. 北京: 机械工业出版社, 1996.
ZHANG Cheng. The Theory and Application of Brushless DC Motor[M]. Beijing: Mechanism Industry Press, 1996.
[2]唐任远. 现代永磁电机—理论与设计[M]. 北京: 机械工业出版社, 1997.
TANG Ren-yuan. Modern Permanent Magnet Machines—theory and Design[M]. Beijing: Mechanism Industry Press, 1997.
[3]张相军, 陈伯时, 朱平平. 无刷直流电机换相转矩脉动的分析及其补偿方法[J]. 电工技术杂志, 2000(8): 13-15.
ZHANG Xiang-jun, CHEN Bo-shi, ZHU Ping-ping. An analysis and a compensatioln method for commutation torque ripple in trapezoidal BLDC motor[J]. Electro-technical Journal, 2000(8): 13-15.
[4]Song J H, Choy I. Commutation torque ripple reduction in brushless DC motor drives using a single DC current sensor[J]. IEEE Trans on Power Electr, 2004, 19(2): 312-319.
[5]Carlson R, Lajoie-Mazenc M, Joao C, et al. Analysis of torque ripple due to phase commutation in brushless dc machines[J]. IEEE Trans on Ind Appl, 1992, 28(3): 632-638.
[6]Matsui n, Ohashi H. DSP based adaptive control of brushless motor[a]. IEEE IAS’88[C]. Pittsburgh, 1988. 375-380.
[7]Kim K H, Chung S K, Moon G W. Parameter estimation and control of permanent magnet synchronous motor drive using model reference adaptive technique[A]. IECON’95[C]. Orlando, 1995. 387-392.
[8]Li F J, Lin Y S. A robust PM synchronous motor drive with adaptive uncertainty observer[J]. IEEE Trans on Energy Conversion, 1999, 14(6): 989-995.
[9]Elbuluk M E, LIU Tong, Husain I. Neural-network-based model reference adaptive systems for high-performance motor drives and motion controls[J]. IEEE Trans on Ind Appl, 2002, 38(3): 879-886.
[10]Weisgerber S, Proca A, Keyhani A. Estimation of permanent magnet motor parameters[A]. IEEE IAS Annual Meeting[C]. New Orleaus, 1997. 29-34.
[11]Nakano M. Application of H∞ control to motor speed control system[A]. IECON’91[C]. Tokyo, 1991. 839-842.
[12]韩曾晋. 自适应控制[M]. 北京: 清华大学出版社, 1995.
HAI Zeng-jin. Adaptive Control[M]. Beijing: Tsinghua University Press, 1995.
[13]Tsakalis K S. Robustness of model reference adaptive controllers: an input-output approach[J]. IEEE Trans on Auto Contr, 1992, 37(5): 556-565.
收稿日期:2005-01-28
基金项目: 高等学校优秀青年教师教学科研奖励计划项目(文教司[2001]183)
作者简介: 揭贵生(1976-), 男, 湖南澧县人, 博士研究生, 从事电力电子与电气传动控制技术研究
论文联系人: 揭贵生, 男, 博士研究生; 电话: 027-62997980(O); E-mail: zhenyujiel@sohu.com