基于误差最小化的新型迭代学习算法
肖擎纲1, 2,曾阳素1
(1. 湖南师范大学 物理与信息科学学院,湖南 长沙,410081;
2. 湖南邵阳医学高等专科学校 计算机网络中心,湖南 邵阳,422000)
摘 要:采用1种新方法对基于时间域内二次型性能函数的最优迭代学习算法进行研究,并采用仿真实例对该方法进行验证。该方法的基本原理是:以整个学习过程输出误差的最小化为目标,并以控制增量的二次型作为函数得到新的性能函数进行分析和设计,研究确定以及不确定性线性离散系统的最优迭代学习律、保性能迭代学习律的设计优化问题。研究结果表明:采用这种新方法可使输出误差很小;仿真结果证明了该算法的正确性和有效性。
关键词:LMI方法;迭代学习;函数;算法;误差
中图分类号:TP391 文献标识码:A 文章编号:1672-7207(2008)02-0356-06
A new iteration learning algorithm based on smallest erroneous
XIAO Qing-gang1, 2, ZENG Yang-su1
(1. College of Physics and Information Science, Hunan Normal University, Changsha 410081, China;
2. Center of Computer Network, Hunan Shaoyang Medicine College, Shaoyang 422000, China)
Abstract: A new optimal iterative learning algorithm was proposed in the time domain of a linear quadratic performance function, and it is used to simulate some examples. The main contents of this method are as follows: optimizing question to the iteration learning control, aiming at the smallest outlet error of the entire learning process, analyzing and designing new performance function based on punish function of control’s increase of a linear quadratic. The results show that the output error is the smallest using the new method. Simulation results prove the algorithm is accurate and valid.
Key words: LMI method; iteration learning; function; algorithm; error
基于时间域内二次型性能函数离散系统方程 的最优迭代学习算法
的最优迭代学习算法
设计,从理论上或者实际应用上是很有价值和意 义的。另外,W. G. Seo等[1-5]基于性能函数

给出了另一类最优迭代学习控制设法。对其设计机理的直观解释就是:给出控制量uk+1(i)的具体形式,使
得第k+1次迭代输出误差在学习区间[0, N]内的均方和达到极小,同时,以uk+1(i)相对于uk(i)的增量作为罚函数。在此,本文作者从学习的整个过程来考虑迭代学习控制的最优化问题,即以整个学习过程输出误差的最小化为目标,并以控制增量的二次型作为罚函数。于是,得到新的性能函数离散系统:
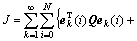
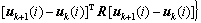 。 (1)
。 (1)
考虑任意采样点 ,得到迭代轴上二次型性能函数:
,得到迭代轴上二次型性能函数:

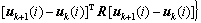 。 (2)
。 (2)
式中:Q和R均为正定对称矩阵。
迭代域内二次型性能的最优化问题,就是基于性能函数(1)或(2)设计新的迭代学习律,使得性能J或 J(i)( )极小。基于性能函数(1)或(2)进行设计可以很方便地调节学习速度,性能矩阵R相对Q越小,学习速度越快。
)极小。基于性能函数(1)或(2)进行设计可以很方便地调节学习速度,性能矩阵R相对Q越小,学习速度越快。
1 系统描述
为了描述方便,先考虑线性连续系统:
 (3)
(3)
式中: ;x(t),y(t)和u(t)分别表示系统状态、输出及控制输入。第k次迭代时,系统模型可表示为:
;x(t),y(t)和u(t)分别表示系统状态、输出及控制输入。第k次迭代时,系统模型可表示为:
 (4)
(4)
由式(4)得到误差模型:
 (5)
(5)
由式(4)或(5)得:
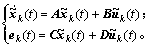 (6)
(6)
式中: ;
;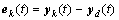 ;
;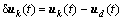 ;
; ;
; 。
。
于是,仿照性能函数(2),定义连续系统(3)的性能函数:
 。 (7)
。 (7)
针对系统(3),要实现迭代学习控制过程最优化,也就是设计相应的迭代学习律,使得对于任意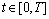 ,当k→∞时,J(t)达到极小。
,当k→∞时,J(t)达到极小。
再考虑一般形式的线性离散系统:
 (8)
(8)
式中: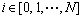 ;状态变量
;状态变量 Rn;输出变量
Rn;输出变量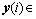 Rm;输入变量
Rm;输入变量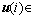 Rr;A,B,C和D为相应维数的系数矩阵。由式(6)有:
Rr;A,B,C和D为相应维数的系数矩阵。由式(6)有:
 ;
;  (9)
(9)

 ; (10)
; (10)
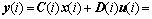
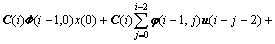
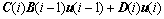 。 (11)
。 (11)
其中:i≥2; , j≤i;
, j≤i;
 。
。
由式(9)~(11)得第k次迭代时的状态误差、输出 误差:
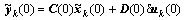 ; (12)
; (12)
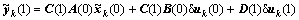 ; (13)
; (13)
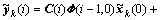

 。 (14)
。 (14)
其中:i≥2; ;
;
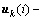
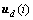 ;
; ;xd(i),ud(i)和yd(i)分别表示第i采样时刻系统状态、控制输入与输出的期望值。由式(12)~(14)可得:
;xd(i),ud(i)和yd(i)分别表示第i采样时刻系统状态、控制输入与输出的期望值。由式(12)~(14)可得:
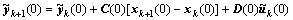 ; (15)
; (15)

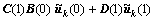 ; (16)
; (16)
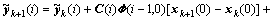
 +
+
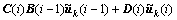 。 (17)
。 (17)
其中:i≥2;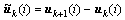 ,表示第i采样时刻,第k+1次迭代时的控制输入相对于第k次迭代控制输入的增量,其具体形式即为本文要求取的迭代学习律。
,表示第i采样时刻,第k+1次迭代时的控制输入相对于第k次迭代控制输入的增量,其具体形式即为本文要求取的迭代学习律。
依据式(1)定义性能函数:
 。 (18)
。 (18)
或写成批量形式为:
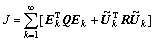 。 (19)
。 (19)
其中:误差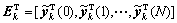 ;控制输入修正量
;控制输入修正量 ;性能参数矩阵
;性能参数矩阵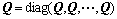 ,
,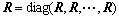 分别为N+1项Q和R组成的分块对角矩阵,同样也是正定对称的。最优迭代学习算法设计问题就是寻找
分别为N+1项Q和R组成的分块对角矩阵,同样也是正定对称的。最优迭代学习算法设计问题就是寻找 的具体表示式,使得性能函数J极小。
的具体表示式,使得性能函数J极小。
2 确定性系统最优迭代学习算法设计
根据上述分析,迭代轴上线性离散系统(6)的批量误差模型可表示为:

表示相邻2次迭代初始定位差,不失一般性,在处理时可设为均值为零、方差为 的随机变量。
的随机变量。
很明显,系统(20)具有与线性离散时间系统相同的结构形式,这里借鉴离散系统相关成果[6-9]。基于性能函数(19)最优化的迭代学习律设计可由定理1 给出。
定理1 若相邻2次迭代初始定位差 ,则采用迭代学习律:
,则采用迭代学习律:

3 不确定性系统保性能迭代算法设计
式(21)所给出的迭代学习律要求确切知道系统模型G,当模型包含不确定项,且 时,系统(20)可转化为:
时,系统(20)可转化为:

 表示可获得的系统标称模型,
表示可获得的系统标称模型,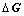 为不确定项。首先进行如下假设。
为不确定项。首先进行如下假设。
假设1 系统模型不确定项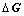 具有如下结构形式:
具有如下结构形式:

在设计前,首先引入如下定义与定理。
定义1 对系统(23)和性能指标(19),若存在矩阵K和正定对称矩阵P,使得对所有非零的Ek,满足:

则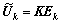 称为系统(23)的一个具有性能矩阵P的保性能迭代学习律。
称为系统(23)的一个具有性能矩阵P的保性能迭代学习律。
保性能迭代学习律、迭代域内二次镇定以及系统性能指标之间的关系由以下定理揭示。
定理2 若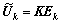 是系统(23)和性能指标(19)的一个具有性能矩阵P的保性能迭代学习律,则对所有允许的不确定性,迭代轴上的误差模型在迭代域内是二次稳定的,且相应的性能指标值满足
是系统(23)和性能指标(19)的一个具有性能矩阵P的保性能迭代学习律,则对所有允许的不确定性,迭代轴上的误差模型在迭代域内是二次稳定的,且相应的性能指标值满足 。其中E1表示第1次迭代时的系统误差。
。其中E1表示第1次迭代时的系统误差。
 (27)
(27)
定理3  是系统(23)的保性能迭代学习律,当且仅当存在常数ε>0,矩阵
是系统(23)的保性能迭代学习律,当且仅当存在常数ε>0,矩阵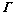 和对称正定矩阵P使得
和对称正定矩阵P使得

4 保性能迭代学习律的优化
定理3给出的保性能迭代学习律设计在一般情况下不一定是惟一的,如下定理给出保性能迭代学习律的优化设计方法。
定理4 对以下优化问题:

5 仿 真
为了验证上述方法的有效性,选取如下离散系统作为仿真实例:
按照上述分析,容易得到系统(4)在迭代轴上批量形式的误差模型。具有形如(19)所示的性能函数,另设系统期望输出yd(i)=i2/100-i+200。在假定系统(29)确定与不确定2种情况下,进行如下仿真。
仿真1 设a=-0.8,b=0.5,c=1,d=1.2。根据定理1设计最优迭代学习律,且选择Q=3I,R=I,I为21×21阶单位矩阵。利用MATLAB及其TOOLBOX中的函数,可得系统性能函数值与迭代学习次数的关系曲线如图1所示,相应的系统输出误差均方和与迭代学习次数的关系曲线如图2所示。若修改性能函数,取Q=3I,R=0.1I,则得到如图3所示的性能函数值与迭代学习次数的关系曲线,相应的系统输出误差均方和与迭代学习次数的关系曲线如图4所示。
比较图2与图4可以看出,性能矩阵R相对于矩阵Q越小,输出误差收敛越快。因而,利用本文方法设计迭代学习律,可以很方便地对学习速度进行调节。
比较图1和图3可知,随着R的减少,性能函数具有明显的收敛效果;从图2与图4可以看出,性能矩阵R相对于矩阵Q越小,输出误差收敛速度越快,输出误差趋于最小。

图1 Q=3I和R=I时性能函数值与迭代次数关系曲线
Fig.1 Relationship between properties value and iterative times when Q=3I and R=I
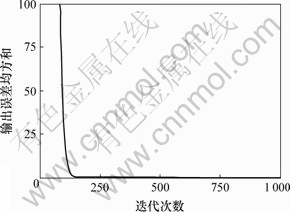
图2 Q=3I和R=I时输出误差均方和与迭代次数关系
Fig.2 Relationship between average error of output and iterative number when Q=3I and R=I
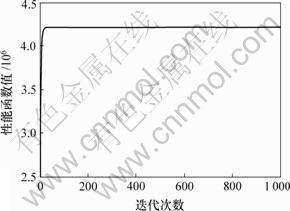
图3 Q=3I和R=0.1I时性能函数值与迭代次数关系曲线
Fig.3 Relationship between properties value and iterative number when Q=3I and R=0.1I
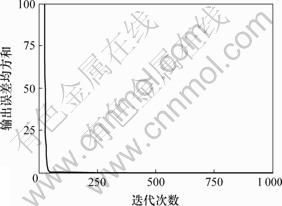
图4 Q=3I和R=0.1I时输出误差均方和与迭代次数关系
Fig.4 Relationship between average error of output and iterative number when Q=3I and R=0.1I
仿真2 进一步考虑系统(29)的不确定性,假设系统标称模型参数分别为:a=-0.8,b=0.5,c=1,d=5。由假设1知,系统模型不确定项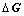 具有如下结构形式:
具有如下结构形式:
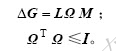
仿真中若仅考虑(29)中输出方程参数d的变化,设 ,则可选取
,则可选取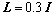 ,
, (I为21×21阶单位矩阵)。根据定理3和定理4设计并优化迭代学习律,取性能矩阵
(I为21×21阶单位矩阵)。根据定理3和定理4设计并优化迭代学习律,取性能矩阵 ,
, ,则得:当
,则得:当 时,针对不确定性系统(23)和性能函数(19),可得到最优保性能迭代学习律
时,针对不确定性系统(23)和性能函数(19),可得到最优保性能迭代学习律 。此时,性能函数值、输出误差均方和与迭代学习次数关系曲线分别如图5和图6所示。可见,随着性能函数参数矩阵的适当调整,性能函数取得好的收敛效果,其输出误差达到最小。
。此时,性能函数值、输出误差均方和与迭代学习次数关系曲线分别如图5和图6所示。可见,随着性能函数参数矩阵的适当调整,性能函数取得好的收敛效果,其输出误差达到最小。

图5 L=0.3I,Q=3I和R=I时性能函数值与迭代次数关系曲线
Fig.5 Relationship between properties value and iterative number when L=0.3I, Q=3I and R=I
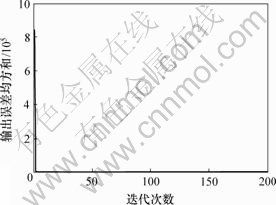
图6 L=0.3I,Q=3I和R=I时输出误差均方和与迭代次数关系
Fig.6 Relationship between average error of output and iterative number when L=0.3I, Q=3I and R=I
6 结 论
a. 在迭代域内先定义了二次型性能函数,针对新的性能函数指标研究了确定、不确定性线性离散系统的最优迭代学习律、保性能迭代学习律的设计优化问题,使得输出误差很小,达到了预期的效果。
b. 所提出的不确定性系统给出的基于LMI方法的保性能迭代学习律设计方法,不仅在理论上容易验证,同时可以使用MATLAB工具箱方便、快速求解。
c. 通过适当调整性能函数中的参数矩阵,使性能矩阵R相对于矩阵Q交换减少,从而使输出误差很快收敛,输出误差最小,同时,控制迭代的学习速度也得到提高。
参考文献:
[1] Seo W G, Park B H, Lee J S. Intelligent learning control for a class of nonlinear dynamics systems[J]. IEE Proc Control Theory Application, 1999, 146(2): 165-170.
[2] 林 辉, 王 林. 迭代学习控制理论[M]. 西安: 西北工业大学出版社, 1998.
LIN Hui, WANG Lin. Control theory of iterative learning[M]. Xi’an: Press of Northwest Industrial University, 1998.
[3] 谢振东, 刘永清. 分布参数系统目标跟踪的二阶P 型学习算法[J]. 暨南大学学报, 1998, 16(1): 42-47.
XIE Zheng-dong, LIU Yong-qing. Distributed parameter system target tracking two steps P learning algorithm[J]. Journal of Jinan University, 1998, 16(1): 42-47.
[4] 杨胜跃, 樊晓平, 年晓红, 等. 基于LMI方法的保性能迭代学习算法设计[J]. 自动化学报, 2006, 32(4): 578-585.
YANG Sheng-yue, FAN Xiao-ping, NIAN Xiao-hong, et al. Designing of guaranteed cost iterative learning algorithms based on LMI method[J]. Acta Automatica Sinica, 2006, 32(4): 578-585.
[5] 刘 颖, 李正飞, 曾光宇. 数字图像重建的迭代算法研究及仿真[J]. 机械工程与自动化, 2006(4): 37-39.
LIU Ying, LI Zheng-fei, XIAO Guang-yu. Study and simulation on the ART algorithm of figure image reconstruction[J]. Mechanical Engineering and Automation, 2006(4): 37-39.
[6] 俞 立. 不确定离散系统的最优保性能控制[J]. 控制理论与应用, 1999, 16(5): 639-642.
YU Li. Indefinite separate system optimal performance control[J]. Control Theory and Application, 1999, 16(5): 639-642.
[7] 周其节, 徐建闽. 柔性机机器人的控制[J]. 控制理论与应用, 1994, 11(2): 226-228.
ZHOU Qi-jie, XU Jian-min. Control of flexibility machine robot[J]. Control Theory and Application, 1994, 11(2): 226-228.
[8] 樊晓平, 徐建闽, 周其节, 等. 柔性机器人的动力学建模及控制[J]. 控制理论与应用, 1997, 14(3): 318-329.
FAN Xiao-ping, XU Jian-min, ZHOU Qi-jie, et al. Dynamics modeling and control of flexible robot[J]. Control Theory and Application, 1997, 14(3): 318-329.
[9] YU Li, WANG Jin-cheng, CHU Jian. Guaranteed cost control of uncertain linear discrete-time systems[C]//Proceedings of American Control Conference. Albuquerque, 1997: 3181- 3184.
[10] Gunnarsson S, Norrlof M. On the design of ILc algorithms using optimization[J]. Automatica, 2001, 37(12): 2011-2016.
[11] Norrlof M. An adaptive iterative learning control algorithm with experiments and industrial robot[J]. IEEE Transactions on Robotics and Automation, 2002, 18(2): 245-251.
[12] Frueh J A, Phan M Q. Linear quadratic optimal learning control[J]. International of Control, 2000, 73(10): 832-839.
[13] CHENG Shao, RONG Gao-fu, YANG Yi. Robot stability of optimal iterative learning control and application to injection molding machine[J]. Automatica, 2003, 29(1): 73-79.
[14] 陈若珠, 艾文欢, 李战明. 一种改进的非线性离散系统迭代学习控制算法[J]. 科学技术与工程, 2007, 22(7): 5776-5780.
CHEN Ruo-zhu, AI Wen-huan, LI Zhan-ming. Improved iterative learning control algorithm for nonlinear discrete systems[J]. Science and Technology and Engineering, 2007, 22(7): 5776-5780.
收稿日期:2007-07-16;修回日期:2007-09-26
基金项目:湖南省自然科学基金资助项目(05F0018)
通信作者:肖擎纲(1956-),男,湖南邵阳人,副教授,硕士研究生,从事计算机应用技术和光信息技术研究;电话:0739-5395956;E-mail: shaojiew@163.com