采用边坡稳定性强度折减法分析弹性应变能突变判据

柴红保^{1, 2}，曹  平¹，林  杭¹，赵延林¹

(1. 中南大学 资源与安全工程学院，湖南 长沙，410083；

2. 湖南科技大学 能源与安全工程学院，湖南 湘潭，411201)

摘  要：为分析采用强度折减法确定边坡安全系数过程中边坡弹性应变能随折减系数变化与边坡失稳破坏的内在联系，建立数值模型，记录边坡弹性应变能与折减系数关系曲线；通过对某边坡的分析，绘制弹性应变能与折减系数关系曲线。研究结果表明：采用强度折减法，当边坡处于稳定状态时，折减系数增大引起边坡变形增大，导致边坡体弹性应变能随之增大；但是，边坡岩土体能够承受的弹性应变能是有极限的，当折减系数增大到某一值时，边坡体的弹性应变能达到极限，再增大折减系数将导致边坡失稳破坏；边坡体弹性应变能与折减系数服从指数关系；利用弹性应变能与折减系数关系曲线得到的边坡安全系数与采用其他经典的方法所得边坡安全系数基本一致，弹性应变能随折减系数变化而变化的规律可以作为边坡稳定性强度折减法分析的失稳判据。

关键词：强度折减法；失稳判据；能量；安全系数

中图分类号：TU 452          文献标识码：A         文章编号：1672-7207(2009)04-1054-05

Criteria of elastic strain energy in slope stability analysis using strength reduction method

CHAI Hong-bao^{1, 2}, CAO Ping¹, LIN Hang¹, ZHAO Yan-lin¹

(1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;

2. School of Energy and Safety Engineering, Hunan University of Science and Technology, Xiangtan 411201, China)

Abstract: A calculation model was created to analyze the relationship between elastic strain energy and the reduction coefficient in slope stability analysis using strength reduction method. The relationship between elastic strain energy and the reduction coefficient was recorded. One slope was analyzed, and the curve of the elastic strain energy and the reduction coefficient was plotted. The results show that the elastic strain energy becomes larger with the increase of the strength reduction coefficient when the slope is still in steady state. That the strength reduction coefficient becomes larger causes the strain of the slope and elastic strain energy larger. The elastic strain energy of the slope has a limited point. The biggest value can be gotten when the strength reduction coefficient reaches a value. The slope will slip if the strength reduction coefficient becomes larger. There exists an index relationship between the elastic strain energy and reduction coefficient. The safety factor obtained with the relationship between elastic strain energy and the reduction coefficient is similar to that obtained by other traditional slope steady analyzed method. The relationship between elastic strain energy and the reduction coefficient can be used as criteria in slope stability analysis using strength reduction method.

Key words: strength reduction method; strength reduction failure criteria; energy; safety coefficient

目前，边坡稳定性分析中判断边坡失稳破坏的判据有：边坡内某点的位移与折减系数的关系曲线^[1-2]，广义剪应变贯通^[3-4]，塑性区的范围及其连通状态^[5]，迭代求解的不收敛性^[6-8]等。边坡失稳时，某些物理量的变化和分布特征不依赖于所采用的数值计算手段。采用限定收敛迭代最大次数的判定方法是不合适的；以数值计算中节点不平衡力与外荷载的比值作为边坡失稳破坏依据也具有一定的人为任意性。连镇营等^[9]基于强度折减弹塑性有限元分析结果，绘制边坡内广义剪应变分布，并认为若某一幅值广义剪应变的区域在边坡中相互贯通，则表明边坡已经失稳破坏，由此所确定的边坡安全系数也带有一定的非确定性。赵尚毅等^[10]则认为塑性区从坡脚到坡顶贯通并不一定意味着边坡破坏，塑性区贯通是破坏的必要条件，但不是充分条件，还要看是否产生很大的且无限发展的塑性变形和位移。在边坡变形破坏过程中应力应变状态十分复杂，具有一定的不确定性，因此，简单地以应力或应变作为破坏判据不适合。实际上，岩石的破坏归根到底是能量驱动下的一种状态失稳现象。可见，若能详细分析岩石变形破坏过程中的能量传递与转化，建立以能量变化为破坏判据的强度理论，则有可能真实地反映岩石的破坏规律^[11-12]。为此，本文作者采用边坡变形过程中的能量突变作为边坡破坏的 判据。

1  强度折减过程中边坡体弹性应变能

1.1  强度折减法

抗剪强度折减系数的概念是由Zienkiewicz等^[13]提出的，由此所确定的强度储备安全系数与Bishop所提出的稳定安全系数在概念上是一致的。抗剪强度折减系数^[14]是指在外荷载保持不变的情况下，边坡体所发挥的最大抗剪强度与外荷载所产生的实际剪应力 之比。

1.2  弹性应变能

设弹性体只在某一个方向如x方向受到均匀的正应力为σ_x，相应的正应变为ε_x，则其每单位体积中具有的形变势能即形变势能密度或比能为σ_xε_x/2 (这里假定物体在弹性受力过程中始终保持平衡，因而动能没有改变，而且弹性体的非机械能也没有改变，因此，外力减少的势能完全转化为形变势能)。设弹性体承受全部6个应力分量σ_x，σ_y，σ_z，τ_xz，τ_yz和τ_xy作用，则根据能量守恒定律，得出全部形变势能密度(U₁)：

通常物体受力并不均匀，各个应力分量和形变分量都是位置坐标的函数，因而，形变势能也是位置坐标的函数。为了得出物体全部弹性变形势能，必须将形变势能在整个物体的体积内进行积分，整体的弹性变形势能为

FLAC^3D软件采用的是塑性增量法，使用的是每一个计算时步的变形增量，这导致不能直接使用应变进行能量计算，而弹性应变能也可用应力分量来表示：

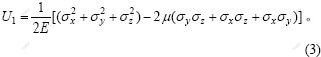
由式(2)得：

由式(4)，可以直接使用应力分量计算变形能量。

1.3  边坡变形过程中变形能量特征

岩石的破坏归根到底是能量驱动下的一种状态失稳现象。岩石材料在变形破坏过程中始终不断与外界交换物质和能量，外载提供的机械能、热能等能量与材料的内能处于一种动态平衡。外载对材料所做的功一部分转化为弹性应变能储存起来，另一部分转化为材料的耗散能。能量耗散是材料变形破坏的本质属性，它反映了材料内部微缺陷的不断发展，强度不断弱化并最终丧失的过程；而变形过程中储存的弹性应变能在破坏时将全部释放出来。可见，能量耗散和能量释放伴随着材料的整个变形过程，并体现了材料性质的不断变化过程^[15]。

2  某边坡强度折减时弹性应变能变化规律

选取某均质边坡作为分析对象，该边坡高为20 m，边坡角为45?。按照平面应变建立FLAC^3D计算模型，模型共计576个单元，1 270个节点。边界条件为：下部固定，左右两侧为水平约束，上部为自由边界。计算模型和图层参数见图1。

土层参数：弹性模量E=10 MPa；泊松比μ=0.3；粘聚力c=

42 kPa；内摩擦角φ=17?；重度2.5 kN/m³

图1  边坡计算模型

Fig.1  Calculation model of slope

2.1  强度折减时边坡体弹性应变能变化趋势

利用FISH语言编写的FLAC^3D程序计算边坡的弹性应变能。该程序能够计算每一个单元的弹性应变能，把所有单元弹性应变能累加即可以得到整个边坡的弹性应变能。该程序可以记录每个折减系数对应的边坡弹性应变能。

利用强度折减法以一定步长增大折减系数，使折减系数由0.9变化到2.6。在采用强度折减法分析边坡稳定性过程中，当折减系数小于1.6时，边坡处于弹性稳定状态。当折减系数低于1.6时，边坡弹性应变能经过一定的计算时步后将处于稳定状态。随着折减系数的增大，边坡弹性应变能不断增大。当折减系数达到1.6时，边坡体的弹性应变能达到最大值；当折减系数继续增加时，边坡体内积聚的弹性应变能不断减小。利用该程序对图1所示模型进行计算分析，得到弹性变形能e与折减系数f的关系，如图2所示，折减系数由初始值增加，边坡弹性应变能增大，当弹性变形能增大到某一极值时，随着折减系数增大，边坡弹性应变能逐渐减小。

图2  边坡弹性变形能与折减系数的关系

Fig.2  Relationship between elastic strain energy of slope and reduction coefficient

2.2  边坡弹性应变能变化规律

在岩体工程中，不同的应力状态允许储存不同的应变能。或者说，一定的应力状态具有一定的极限储存能。岩石试块破断时总的应变能即为该应力状态下的极限储存能。

采用强度折减法分析边坡稳定性时，原岩强度较大，变形较小，岩体中储存的弹性应变能也较小；随着折减系数增大，岩体强度降低，变形不断增大，岩体中储存的弹性应变能也不断增加。但是，能量集聚是有条件的，即集聚的弹性变形能不允许超过该应力状态下的极限储存能。工程围岩各点的应力状态各不相同，围岩各点的允许储存能也互不相同。愈接近滑动带，围岩的最小主应力增加得愈多，能够储存的能量(即极限储存能)也愈多。若集聚能大于该点的极限储存能，则多余的能量将被释放和转移。所释放的能量和转移的能量将造成岩体塑性变形或破裂。

2.3  折减系数与变形能量的关系

边坡弹性应变能量与折减系数服从如下函数关系：

当e取最大值时，对应的折减系数即为边坡的安全系数。式(5)对应的函数曲线见图3。

图3  边坡弹性应变能与折减系数的关系

Fig.3  Relationship between elastic strain energy of slope and reduction coefficient

当折减系数逐渐增大时，边坡的弹性应变能逐渐增大。这是由于强度折减引起边坡变形增大，从而导致边坡体内的弹性应变也逐渐增大。但是，边坡体能够承受的弹性应变能是有极限的，随着折减系数的增大，边坡体内的弹性应变能不断增大，当折减系数达到某一值时，边坡体内积聚的弹性应变能也达到极限值，再增大折减系数，边坡体内积聚的弹性应变能将超过坡体能够存储的最大弹性应变能极限，导致坡体破坏失稳；边坡体失稳破坏后，它积聚的弹性应变能便急剧减小。在这个过程中，当边坡体积聚的弹性应变能达到极限值时，边坡处于极限平衡状态，此时，对应的强度折减系数就是边坡的安全系数。

3  实例分析

3.1  计算模型

某一均质土坡，坡高H=20 m，粘聚力c=42 kPa，土的容重γ=20 kN/m³，内摩擦角为17?，求坡角β分别为30?，35?，40?，45?和50?时边坡的稳定安全系数以及对应的滑动面。

按照平面应变建立模型，如图4所示。边界条件为：左右两侧水平约束，下部固定，上部为自由边界，坡体材料为摩尔库仑材料。采用非关联流动法则进行分析。

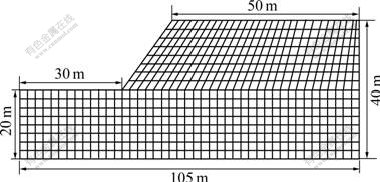
土层参数：边坡角β=50?；泊松比μ=0.3；粘聚力c=42 kPa；内摩擦角φ=17?；容重为20 kN/m³

图4  边坡计算模型

Fig.4  Calculate model of slope

3.2  安全系数计算结果

不同折减系数对应的弹性应变能见表1，其中：由表2中前面3种方法得到的安全系数为各屈服准则采用非关联流动法则(膨胀角ψ=0?)时所得的安全系  数^[10]。表2中，DP1为外接圆DP准则，DP2为摩尔-库仑等面积圆DP准则，DP3为平面应变条件下的摩尔-库仑匹配DP准则。传统极限平衡条分法安全系数计算采用的软件为加拿大的边坡稳定分析程序SLOPE/W。

表1  不同折减系数对应的弹性应变能

Table 1  Different elastic strain energies with different reduction coefficients

边坡弹性应变能与折减系数的函数关系为：

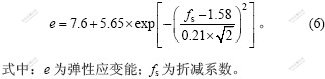
当折减系数f_s=1.58时，e取极值，此时，边坡处于极限平衡状态，这个折减系数就是该边坡的安全系数。采用不同方法求得的安全系数见表2。

表2  不同方法求得的安全系数

Table 2  Safety factors by different methods

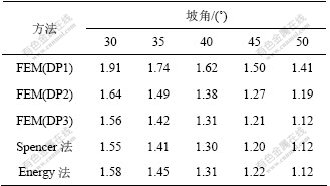
从表2可以看出，利用边坡强度折减过程中弹性应变能的变化规律判定得到的安全系数与Spencer法所得安全系数的相对误差为2%左右，以能量变化为判据所确定的强度折减法分析边坡稳定性的安全系数与采用极限平衡法得到的结果十分相近。利用强度折减法分析边坡稳定性时，边坡体内弹性应变能的变化规律可以作为边坡失稳破坏的依据，也可以作为确定强度折减法分析边坡安全系数的判据。

4  结  论

a. 采用强度折减法，边坡体内弹性应变能与折减系数呈指数关系，随着折减系数的增大，坡体内塑性区的应变能会发生突变，在发生突变的这一点对应着的折减系数即为边坡的安全系数。

b. 当折减系数较小，边坡没有被破坏时，随着折减系数的增大，边坡体的变形量不断增大，引起边坡弹性应变能不断增加。在该阶段，边坡体弹性应变能经过一定计算时步后都将处于稳定状态。

c. 在强度折减过程中，边坡体弹性应变能的突变点对应的折减系数即为边坡的安全系数。在该点，边坡体内的弹性应变能达到该坡体能够存储的弹性应变能的极限值，再增大折减系数，坡体内存储的弹性应变能将超过边坡体存储弹性应变能的极限，会引起边坡体失稳破坏。

d. 使用强度折减法时，以边坡体弹性应变能突变作为判据确定边坡安全系数与采用简化Bishop法和非线性迭代收敛性失稳评判准则所得到的计算结果比较接近，边坡体弹性应变能的突变可用于确定边坡安全系数。

参考文献：

[1] Griffiths D V, Lane P A. Slope stability analysis by finite elements[J]. Geotechnique, 1999, 49(3): 387-403.

[2] 张培文, 陈祖煜. 糯扎渡大坝设计边坡稳定的有限元分析[J]. 中国水利水电科学研究院学报, 2003, 1(3): 207-210.
ZHANG Pei-wen, CHEN Zu-yu. Finite element analysis of slope stability in Nuozhadu dam design[J]. Journal of China Institute of Water Resources and Hydropower Research, 2003, 1(3): 207-210.

[3] Ugai K, Leshchinsky D. Three dimensional limit equilibrium and finite element analysis: a comparison of results[J]. Soils and Foundations, 1995, 35(4): 1-7.

[4] Dawson E M, Roth W H, Drescher A. Slope stability analysis by strength reduction[J]. Geotechnique, 1999, 49(6): 835-840

[5] 郑颖人, 赵尚毅, 张鲁渝. 用有限元强度折减法进行边坡稳定分析[J]. 中国工程科学, 2002, 4(10): 57-61.
ZHENG Ying-ren, ZHAO Shang-yi, ZHANG Lu-yu. Slope stability analysis by strength reduction FEM[J]. Engineering Science, 2002, 4(10): 57-61.

[6] 孙 伟, 龚晓南. 弹塑性有限元法在土坡稳定分析中的应用[J]. 太原理工大学学报, 2003, 34(2): 199-202.
SUN Wei, GONG Xiao-nan. Application of elasto-plastic finite element method in stability analysis of soil slopes[J]. Journal of Taiyuan University of Technology, 2003, 34(2): 199-202.

[7] 栾茂田, 武亚军, 年廷凯. 强度折减有限元法中边坡失稳的塑性区判据及其应用[J]. 防灾减灾工程学报, 2003, 23(3): 1-8.
LUAN Mao-tian, WU Ya-jun, NIAN Ting-kai. A criterion for evaluating slope stability based on development of plastic zone by shear strength reduction FEM[J]. Journal of Disaster Prevention and Mitigation Engineering, 2003, 23(3): 1-8.

[8] 林 杭, 曹 平, 赵延林, 等. 强度折减法在 Hoek-Brown 准则中的应用[J]. 中南大学学报: 自然科学版, 2007, 38(6): 1219-1224.
LIN Hang, CAO Ping, ZHAO Yan-lin, et al. Strength reduction method applied in Hoek-Brown criteria[J]. Journal of Central South University: Science and Technology, 2007, 38(6): 1219-1224.

[9] 连镇营, 韩国城, 孔宪京. 强度折减有限元法研究开挖边坡的稳定性[J]. 岩土工程, 2001, 23(4): 407-411.
LIAN Zhen-ying, HAN Guo-cheng, SUN Xian-jing. Stability analysis of excavation by strength reduction FEM[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(4): 407-411.

[10] 赵尚毅, 郑颖人, 张玉芳. 极限分析有限元法讲座—Ⅱ有限元强度折减法中边坡失稳的判据探讨[J]. 岩土力学, 2005, 26(2): 332-336.
ZHAO Shang-yi, ZHENG Ying-ren, ZHANG Yu-fang. Study on slope failure criterion in strength reduction finite element method[J]. Rock and Soil Mechanics, 2005, 26(2): 332-336.

[11] 谢和平, 彭瑞东. 岩石破坏的能量分析初探[J]. 岩石力学与工程学报, 2005, 24(15): 2603-2608.
XIE He-ping, PENG Rui-dong. On energy analysis of rock failure[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(15): 2603-2608.

[12] 谢和平, 鞠 杨, 黎立云, 等. 岩体变形破坏过程的能量机制[J]. 岩石力学与工程学报, 2008, 27(8): 1729-1740.
XIE He-ping, Ju Yang, LI Li-yun, et al. Energy mechanism of deformation and failure of rock masses[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(8): 1729-1740.

[13] Zienkiewicz O C, Humpheson C, Lewis R W. Associated and non-associated visco-plasticity and plasticity in soil mechanics[J]. Geotechnique, 1975, 25(4): 671-689.

[14] Duncan J M. State of the art: Limit equilibrium and finite-element analysis of slopes[J]. Journal of Geotechnical Engineering, ASCE, 1996, 122(7): 577-596.

[15] 郑颖人. 岩土材料屈服与破坏及边(滑)坡稳定分析方法研讨——“三峡库区地质灾害专题研讨会”交流讨论综述[J]. 岩石力学与工程学报, 2007, 26(4): 649-661.
ZHENG Ying-ren. Discussion on yield and failure of geomaterials and stability analysis methods of slope/landslide communion and discussion summary of special topic forum on geologic disasters in the Three Gorges Project Region[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(4): 649-661.

收稿日期：2008-08-10；修回日期：2008-11-15

基金项目：国家自然科学基金资助项目(50774093)；高等学校博士学科点专项科研基金资助项目(20060533071)；中国博士后科学基金资助项目(20060400264)；湖南省研究生创新基金资助项目(1343-74236000014)

通信作者：柴红保(1977-)，男，河南南阳人，博士研究生，从事岩土工程研究；电话：13574091922；E-mail: chbmoon@163.com