J. Cent. South Univ. (2020) 27: 2673-2686

DOI: https://doi.org/10.1007/s11771-020-4490-z

Robust force tracking control via backstepping sliding mode control and virtual damping control for hydraulic quadruped robots

SHEN Wei(沈伟)^{1, 2}, LU Xiao-bin(吕晓斌)¹, MA Chen-jun(马琛俊)³

1. Department of Mechatronics Engineering, University of Shanghai for Science and Technology,Shanghai 200093, China;

2. State Key Laboratory of Fluid Power and Mechatronic Systems, Zhejiang University,Hangzhou 310000, China;

3. Libin Technology R&D Center, Shanghai Electric Hydraulic & Pneumatics Co., Ltd.,Shanghai 200237, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020

Abstract: In order to improve the force tracking performance of hydraulic quadruped robots in uncertain and unstructured environments, an impedance-based adaptive reference trajectory generation scheme is used. Secondly, in order to improve the robustness to environmental changes and reduce the contact force errors caused by trajectory tracking errors, the backstepping sliding mode controller is combined with the adaptive reference trajectory generator. Finally, a virtual damping control based on velocity and pressure feedback is proposed to solve the problem of contact force disappearance and stall caused by sudden environmental change. The simulation results show that the proposed scheme has higher contact force tracking accuracy when the environment is unchanged; the contact force error can always be guaranteed within an acceptable range when the environment is reasonably changed; when the environment suddenly changes, the drive unit can move slowly until the robot re-contacts the environment.

Key words: hydraulic quadruped robot; impedance control; backstepping sliding mode control; virtual damping control

Cite this article as: SHEN Wei, LU Xiao-bin, MA Chen-jun. Robust force tracking control via backstepping sliding mode control and virtual damping control for hydraulic quadruped robots [J]. Journal of Central South University, 2020, 27(9): 2673-2686. DOI: https://doi.org/10.1007/s11771-020-4490-z.

1 Introduction

Compared with traditional wheeled robots, quadruped robots have excellent athletic abilities in unknown and unstructured environments, which makes it have broad application prospect in military and civilian fields [1]. Among the common driving methods, hydraulic drive is more suitable for the high-performance requirements of quadruped robot due to its high precision, fast response speed, small size and other advantages [2, 3]. Therefore, the research of hydraulic quadruped robot has attracted extensive attention.

The hydraulic quadruped robot realizes various movements by frequently interacting with the environment surface. Therefore, whether the interaction can be accurately controlled will directly determine the performance of the hydraulic quadruped robot [4]. In this case, it is unreasonable to control the contact force only by using motion control strategy. Because in the process of the interaction between the robot and the external environment, the actual contact force should track the expected value in real time. Too small contact force will cause the task to fail, while excessive contact force will damage the external environment or even the robot itself. The interaction between the robot and the external environment can be described by the contact force [5, 6]. In addition, the quadruped robots often lose stability because of unbalanced contact force. If contact force tracking can be achieved during the interaction, the above-mentioned shortcomings can be overcome.

For a known and static environment, the classic force control strategies can achieve excellent control performance. However, in the unknow and changeable complex environment, coupled with the serious nonlinearity caused by the introduction of the hydraulic drive unit system, it is difficult to achieve excellent force tracking control [7].

In 1985, HOGAN [8] proposed an impedance control strategy for force control. It does not directly control the force and displacement of the system, but establishes and controls the dynamic relationship between them, thereby achieves active flexible control. Then, MAPLES et al [9] summarized the impedance control proposed by HOGAN. They proposed that the stiffness control can be realized by converting the force feedback signals into position errors, and the damping control can be realized by converting the force feedback signals into velocity errors. After that, more and more researchers have sought to achieve contact force tracking within the framework of impedance control.

AREVALO et al [10] discussed the position- based and force-based impedance control methods, introduced the theoretical model of the contact between the legged robot and the environment, and proposed a theoretical control scheme of the general legged robot. CHEN et al [11] proposed a novel fractional-order impedance controller, which effectively reduced the impact and improved the regulation ability of the robot system. KIM et al [12] presented an adaptive boundary energy method, which can ensure the stable contact between the robot and uncertain environment, but cannot achieve variable contact force tracking. ROVEDA et al [13] proposed a force tracking scheme based on optimal impedance. The impedance control gain was analyzed and calculated by LQR optimal control algorithm, and good control performance was achieved in partially uncertain environments. YANG et al [14] proposed an impedance parameter adaptive method based on Q-learning technique, which was implemented based on trajectory tracking errors. On the premise of setting impedance stiffness to zero, DUAN et al [6] and SHENG et al [15] respectively used adaptive impedance damping parameters and fuzzy control to achieve contact force tracking. However, it is unreasonable to set impedance stiffness to zero, because the assumption of zero stiffness does not conform to the intuitive force tracking rule, that is, the creature always maintains stiffness when applying the desired force to the object [16]. LIU et al [17] presented a position-based force control scheme, which had strong robustness under unknown environmental stiffness and variable environmental location, and was successfully applied to constant force tracking. HE et al [18] proposed an adaptive fuzzy neural network control method based on impedance learning. Under uncertain flexible static environment, the robot had better tracking performance. PENG et al [19] presented a position/force tracking impedance control scheme based on adaptive Jacobian matrix and neural network, the robot can achieve contact force tracking under certain external disturbances. KIM et al [20] adopted position-based force tracking impedance control and introduced sliding mode control algorithm to keep the contact force of cleaning robot in the error range when working on different walls. KONG et al [1] simulated the load characteristics of the hydraulic robot drive unit when the environmental structure was changeable. When the load characteristics are known, the proposed force control compensation method has a positive compensation effect. In uncertain environments, ZHANG et al [21] and LIANG et al [16] both proposed an adaptive reference trajectory generation scheme, on which LIANG et al [16] introduced iterative learning algorithm, which further reduced the contact force tracking error.

In general, researchers have carried out extensive and in-depth research on force control in the framework of impedance control, and achieved many results. However, there are few studies on the dynamic force tracking control of hydraulic quadruped robots in complex environments. The existing studies have not considered the negative effects of environmental parameter changes and the inherent nonlinearity of hydraulic systems, nor have they specifically analyzed the cause of force tracking error. As a result, the existing studies are not able to achieve robust force tracking control in complex environments, nor to maintain the safety and stability of the robot when environmental parameters change.

In a real complex environment, environmental parameters are not only unknown, but also changeable. In view of the shortcomings of the above existing research, this paper proposes the following scheme. In the framework of position- based impedance control, an adaptive reference trajectory generator based on Lyapunov function is applied. Secondly, the backstepping sliding mode control algorithm is used to improve the robustness to environmental changes and reduce the contact force tracking errors. Finally, a virtual damping control strategy based on velocity and pressure feedback is proposed to avoid the instability caused by sudden environmental changes.

The scheme proposed in this paper can fundamentally solve the problem that the hydraulic quadruped robot is difficult to achieve robust force tracking in complex environment, and can avoid the instability caused by the sudden change of environmental parameters. While ensuring the safety and stability of the robot, it greatly enhances the adaptability of the hydraulic quadruped robot to the complex environment, and helps to promote the hydraulic quadruped robot to practical applications.

2 Hydraulic drive unit model

Through the cooperative action of the hydraulic driving unit of each joint of the leg, various kinds of motions of the robot are realized. In this paper, an integrated valve controlled symmetrical cylinder with high power density is used as the driving unit of leg joint. The schematic diagram of the hydraulic drive unit control system is shown in Figure 1.

Considering the nonlinearity and time-varying uncertain flow of the hydraulic drive unit system, the uncertain friction force of the hydraulic cylinder and the time-varying contact force from the environment, this paper establishes a mathematical model of the hydraulic drive unit through mechanism analysis.

The nonlinearity of the hydraulic drive unit system mainly comes from the servo valve. The relationship between the flow of the servo valve and the displacement of the valve core can be expressed as:

               (1)

where C_d is the flow coefficient; ω is the servo valve area gradient; x_v is the spool displacement; ρ is hydraulic oil density; P_s is the oil supply pressure; P_L is load oil pressure; P_L=P₁-P₂; P₁ and P₂ are respectively the pressure of two chambers of the hydraulic cylinder. The symbolic function sign() is expressed as:

                       (2)

Considering the time-varying uncertain flow of the actual system [22], the flow continuity equation of the hydraulic cylinder is:

              (3)

where A is the effective area of the piston rod; x,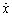and are respectively the displacement, velocity and acceleration of hydraulic cylinder; C_tp is the total leakage coefficient of hydraulic cylinder; V_t is the effective volume; β_e is the oil elastic modulus; W(t) is time-varying uncertain flow.

Considering the time-varying contact force from the environment and the uncertain friction force of the hydraulic cylinder, the force balance equation of the hydraulic cylinder can be expressed as:

                     (4)

where m is converted mass load; b is the damping load; f_a is the uncertain friction force; f_e is the time-varying contact force.

Figure 1 Control system structure schematic diagram (1-Globe valve; 2-Electric motor; 3-Constant pressure variable pump; 4-Filter; 5-Check valve; 6-Hydraulic accumulator; 7-Servo valve; 8-Hydraulic cylinder; 9-Relief valve)

The hydraulic quadruped robot uses the high frequency response servo valve as the leg joint drive unit. Servo valve bandwidth is more than 80 Hz, while the system bandwidth is about 4 Hz. Therefore, the relationship between the displacement of servo valve core x_v and the input signal u can be simplified as a proportion link, that is, x_v=k_iu. Equation (1) can be rewritten as:

                   (5)

where

Choose x₁=x, as the state variables. Through formulas (1)-(5), the state space equation of the whole hydraulic drive unit system can be expressed as:

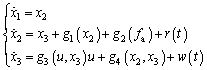           (6)

where

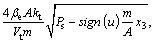
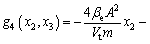
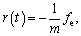
3 Controller design

3.1 Adaptive reference trajectory generator based on impedance control

Position-based impedance control (PBIC) is used in this paper, and the robot’s position control system is well-developed and stable. Compared with the force-based impedance control (FBIC), the position-based impedance control can avoid solving the complex dynamic model of robot. The schematic diagram of position-based impedance control structure of the hydraulic drive unit is shown in Figure 2. It consists of an impedance control outer loop and a position control inner loop. The dynamic relationship between output position and contact force of hydraulic drive unit is adjusted by establishing mass damping spring model.

To simplify the analysis process, consider variables in one direction, and the target impedance model is:

     (7)

where m_d, b_d and k_d are target mass, target damping and target stiffness respectively, x_r is reference trajectories, f_r and f_e are the expected contact force and actual contact force respectively.

Figure 2 Hydraulic drive unit position-based impedance control structure

Common environments can be simplified into a stiffness model:

                           (8)

where k_eis the equivalent stiffness between the foot end of the leg and the environment surface; x_e is environmental location.

After robot’s feet contact with environment is stable, Therefore, Eq. (7) can be rewritten as:

                  (9)

where e_f is the contact force error.

Substituting Eq. (8) into Eq. (9), we can get:

                   (10)

Assume that the expect contact force f_r is a constant, so Meanwhile, after contact is stable,the error equation of steady- state contact force can be obtained as:

                 (11)

where e_fs is the steady-state contact force error.

According to the analysis of Eq. (11), there are two methods to make the error of steady contact force equal to zero. Method 1 is to make the target stiffness k_d=0, and this method is satisfied with any environmental stiffness. Method 2 is to make the reference trajectory x_r satisfy the following equation:

                             (12)

It is unreasonable to set the target stiffness to zero [16], and the leg is expected to maintain a certain stiffness during the interaction with the environment surface. Therefore, the method 2 mentioned above will be used in this paper. In the process of interacting with the environment surface, the position of the end of the leg is adjusted continuously by generating the reference trajectory in real time, so that the contact force error is zero. In order to realize contact force tracking, Eq. (12) needs to be satisfied, but the environmental stiffness k_e and environmental location x_e are unknown quantities and difficult to measure, so it is difficult to calculate accurate reference trajectory online.

According to the previous research results, the environmental stiffness k_e and environmental location x_e can be estimated online by using Lyapunov function, and then the reference trajectory x_r can be calculated indirectly. The complete adaptive reference trajectory generation law is as follows:

 (13)

where is the initial value of equivalent environmental stiffness; is the initial value of environmental location; r₁ and r₂ are positive constants; 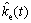is the estimate of environmental stiffness;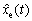is the estimate of environmental location; is the estimate of contact force.

Lyapunov equation is used to estimate the environmental parameters in real time, and then the reference trajectory is calculated in real time to ensureandand finally the force tracking control is realized. However, this scheme does not consider the situation of environmental parameter changes, so in the unknown and changeable environment, the force tracking performance of this scheme is not ideal.

By analyzing the causes of force error, we can know that under the framework of position-based impedance control, the performance of the force tracking control is ultimately determined by the performance of the inner loop position controller.The traditional PID control can not deal with the interference caused by the change of environment parameters and the nonlinearity of hydraulic system, and the robustness is insufficient. Therefore, it is of great significance to improve the accuracy and robustness of the inner loop position controller.

3.2 Backstepping sliding mode control

In this section, on the basis of the adaptive reference trajectory generator, the backstepping sliding mode control (BSSMC) is introduced. The backstepping control can solve the nonlinear problem of complex system very well, and it has very high control precision, so it is very suitable for the control system of hydraulic drive unit. However, the backstepping control can not overcome the disturbance caused by time-varying contact force and depends on the precise control object model, while the sliding mode control is just not sensitive to the disturbance and the change of system parameters [23]. The combination of them can not only overcome the shortcomings of the backstepping control, but also improves the tracking accuracy and the robustness of the control system [24].

When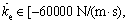 and[-45000 N/m, 45000 N/m] or and 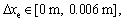it is expected that the controller can still maintain excellent control performance and the contact force tracking error is no more than ±2 N, where is the rate of environmental stiffness change; is the difference between the actual environmental stiffness and the preset environmental stiffness; is the rate of environmental location change; is the difference between the actual environmental location and the preset environmental location.

According to the state space Eq. (6) of the hydraulic drive unit system, the design of the controller can be roughly divided into the following three steps.

Define the position tracking error z₁=x₁-x_d, then where x_d is the ideal position output.

Step 1 Define the Lyapunov equation V₁ of the first-order system:

                               (14)

In order to guarantee define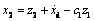, where c₁>0 is a constant, z₂ is a virtual control item and 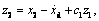then

The derivative of V₁ is obtained as follows:

                      (15)

According to the expression of z₂, the derivative is obtained as follows:

      (16)

Step 2: Define the Lyapunov equation V₂ of the second-order system:

                           (17)

The derivative of V₂ is obtained as follows:

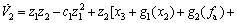
                      (18)

In order to guarantee define  where c₂> 0 is a constant, z₃ is a virtual control item, then the following formulas can be obtained:

 (19)

Define the switching function s:

                        (20)

where k₁>0 and k₂>0 are constants.

Step 3: Define the Lyapunov equation V₃ of the third-order system:

                        (21)

The derivative of V₃ is obtained as follows:

         (22)

According to formula (22), the designed control law can be obtained:

                    (23)

whereis an integrated disturbance item; h and β are positive constants.

Insert formula (23) into formula (22).

         (24)

Define the matrices Q and Z^T as:

           (25)

                        (26)

Due to

             (27)

Combining formula (24) and formula (27), the following inequality can be obtained.

                      (28)

The third-order system has been reversed to the entire hydraulic drive unit system. In order to make the entire system is stable, i.e., 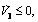we only need to ensure that the matrix Q is positive definite, due to:

 (29)

By guaranteeing |Q|>0, the matrix Q can be positively definite and the system is gradually stable. Therefore, the selection of controller parameters needs to satisfy the following inequalities.

           (30)

The contact force tracking control based on adaptive reference track generator and BSSMC has satisfactory performance. However, in an unstructured and complex environment, the environmental parameters are changeable. For example, during the interaction between the robot and the environment surface, when the environment surface suddenly sinks, the contact force will inevitably fail to track the desired contact force. At this time, the control target should be changed to maintain the stability of the robot, so that the legs slowly touch the ground again.

3.3 Virtual damping control

When the environment surface suddenly sinks and the robot’s legs slip, the contact force of the legs will disappear instantly, and the hydraulic drive unit will stall. This will cause the legs to re-touch the ground at a very high speed and damage the robot’s leg structure. Therefore, when the above situation occurs, the hydraulic drive unit of the robot leg needs to have additional damping characteristics to limit its speed, avoid stalling, and maintain the stability and structural safety of the robot [25]. In response to the above problems, a virtual damping control method based on speed and pressure feedback is proposed.

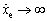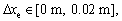Whenandthe hydraulic drive unit needs to have enough damping characteristics to allow the end of the hydraulic drive unit to move slowly until it touches the ground again.

Since the piston reciprocates in the oil, the hydraulic drive unit has damping characteristics. However, compared with the damping required by the quadruped robot joints, the damping of the hydraulic drive unit is small and negligible [25]. Therefore, the virtual damper b_v shown in Figure 3 needs to be built on the hydraulic cylinder to ensure the damping characteristics required by the drive unit.

To obtain the damping characteristics shown in Figure 3, a new force balance equation is constructed.

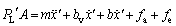              (31)

Figure 3 Virtual impedance schematic

According to the above formula (31), the load pressure of the hydraulic drive unit system when using virtual damping control can be expressed as:

               (32)

Further, referring to Eqs. (1) and (3), the flow equation of the hydraulic drive unit system when using virtual damping control can be expressed as:

                (33)

According to Eq. (4), the load pressure of the hydraulic drive unit system without virtual damping control can be expressed as:

                    (34)

Similarly, according to Eqs. (1) and (3), the flow equation of the hydraulic drive unit system without virtual damping control can be expressed as:

                 (35)

By comparing and analyzing Eqs. (33) and (35), it is not difficult to see that due to the existence of virtual damper, the increase of hydraulic drive unit load pressure leads to the decrease of servo valve flow, this will suppress the speed of the hydraulic drive unit and ultimately ensure that the legs can slowly and steadily re-contact the environmental surface. However, there is no such virtual damper in the actual hydraulic drive unit system, so it is necessary to adjust the input signal of the servo valve to make the hydraulic drive unit exhibit additional damping characteristics.

According to Eq. (33), when virtual damping control is adopted, the spool displacement can be expressed as:

                  (36)

According to Eq. (35), when virtual damping control is not adopted, the spool displacement can be expressed as:

                  (37)

Therefore, the compensation value of spool displacement under virtual damping control is:

                           (38)

The corresponding servo valve input signal compensation value is:

                              (39)

Then, the following formula can be obtained:

 (40)

Therefore, by adjusting the input signal of the servo valve with Eq. (40), the virtual damping control of the hydraulic drive unit system can be realized.

Finally, the complete control structure diagram is shown in Figure 4. It also consists of an outer loop controller and an inner loop controller. The outer loop controller includes an impedance controller and an adaptive reference trajectory generator, and the inner loop controller includes a backstepping sliding mode controller and a virtual damping controller.

4 Simulation

The mass of one leg of a hydraulic quadruped robot is 25 kg, which is equivalent to the load mass of 5 kg on the leg. The leg touches the ground smoothly at a slow speed. The contact force only acts on the foot end in the vertical direction. At this time, the contact force is about 300 N. In practical engineering applications, the hydraulic quadruped robot travels in a complex environment. The robot needs to have the ability of dynamic force tracking to meet different task requirements, so f_r=300+60 sin(πt) N is selected as the control target. The parameters of the hydraulic drive unit system model can be seen in Table 1 and the controller parameters can be seen in Table 2.

In this simulation, the contact environment is equivalent to the stiffness model, and the environmental stiffness k_e=100000 N/m, and the environmental location x_e=0.01 m. The fixed reference trajectory x_r=0.0136 m, and the position tracking curves and contact force tracking curves of the robot hydraulic drive unit can be seen in Figures 5 and 6. The hydraulic drive unit moves from free space to contact with the environment surface, but the actual contact force cannot track the expected contact force. Through analysis, it can be concluded that the fixed reference track x_r is not appropriate, and only by setting impedance parameter k_d to zero or giving precise x_r can achieve zero contact force tracking error. Therefore, a useful reference trajectory generator is designed to achieve accurate contact force tracking.

Figure 4 Complete control structure

Table 1 System parameters

Table 2 Controller parameters

Figure 5 Position tracking curves with fixed x_r=0.0136 m

The adaptive reference track generator generates variable x_r, the position tracking curves, and the contact force tracking curves of the robot hydraulic drive unit can be seen in Figures 7 and 8.

Figure 6 Contact force tracking curves with fixed x_r=0.0136 m

Compared with fixed x_r, the proposed adaptive reference trajectory generation scheme generates accurate x_r through real-time estimation of environmental stiffness, environmental position and contact force, thus achieving better contact force tracking performance. Although the adaptive reference trajectory generation scheme has excellent contact force tracking performance, contact force tracking errors still exist, as shown in Figures 7 and 8. After analysis, the residual contact force error is mainly caused by position tracking error, which has been discussed and studied in Section 3.

Considering the nonlinearity of the hydraulic drive unit system and the time-varying contact force from the environment, Section 3 of this paper redesigns the position controller of the inner loop through the backstepping sliding mode control algorithm to improve the contact force tracking performance. The simulation results can be seen in Figures 9-12, and the simulation conditions are the same as before. The simulation results show that the contact force tracking error is less than 1 N after the introduction of backstepping sliding mode control, which has better contact force tracking performance compared with PID controller, and basically eliminates the contact force tracking error.

Figure 7 Position tracking curves with variable x_r

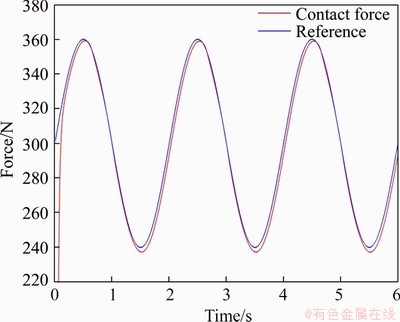
Figure 8 Contact force tracking curves with variable x_r

Figure 9 Position tracking curves with BSSMC and PID controller

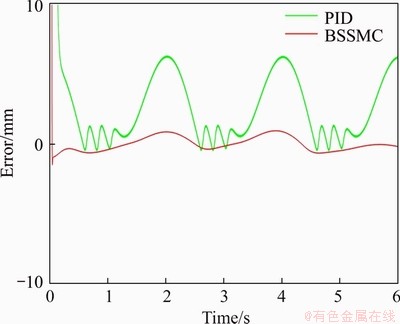
Figure 10 Position tracking error curves with BSSMC and PID controller

Figure 11 Contact force tracking curves with BSSMC and PID controller

Figure 12 Contact force tracking error curves with BSSMC and PID controller

In a complex environment, the environmental parameters are not only unknown, but also changeable, so it is necessary to verify the robustness of the proposed backstepping sliding mode control scheme. The changing curves of environmental stiffness and environmental location can be seen in Figures 13 and 16. The corresponding simulation results when environmental stiffness changes can be seen in Figures 14 and 15, and the corresponding simulation results when environmental location changes are shown in Figures 17 and 18. Simulation results show that the proposed backstepping sliding mode control can still maintain satisfactory contact force tracking performance with no more than ±2 N contact force error when environmental parameters change. Compared with PID controller, the backstepping sliding mode controller has better robustness.

In an unstructured and complex environment,when the environment surface suddenly sinks and the robot’s legs slip, the contact force of the legs will disappear instantly, and the hydraulic drive unit will stall. This will cause the legs to re-touch the ground at a very high speed and damage the robot’s leg structure. By designing the following simulation to verify the damping characteristics of the hydraulic drive unit given by the virtual damping control, the simulation results can be seen in Figures 19 and 21.

Figure 13 Environmental stiffness curve

Figure 14 Contact force tracking curves with BSSMC and PID controller

Figure 15 Contact force tracking error curves with BSSMC and PID controller

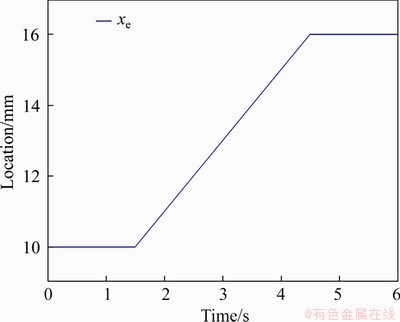
Figure 16 Environmental location curve

Figure 17 Contact force tracking curves with BSSMC and PID controller

Figure 18 Contact force tracking error curves with BSSMC and PID controller

Figure 19 shows the position response curve of the hydraulic drive unit when the virtual damping is set to 0, 20000 and 40000 N·s/m, respectively in the case of x_e=0.002 m and x_r=0.025 m. When the virtual damping is 0 N·s/m, the steady-state time is 130 ms; when the virtual damping is 20000 N·s/m, the steady-state time is 350 ms; when the virtual damping is 40000 N·s/m, the steady-state time is 580 ms. The steady-state time increases with the increase of virtual damping, and the hydraulic drive unit system can exhibit the desired damping characteristics.

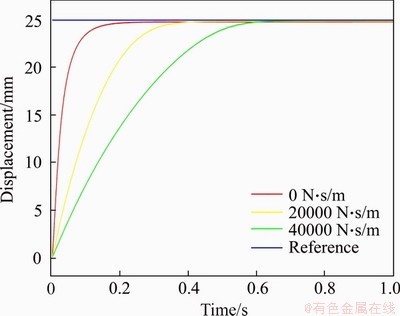
Figure 19 Virtual damping control curves

In the simulation, in order to simulate the sudden sinking of the environment surface and the robot’s legs slipping, the environmental location was suddenly changed from x_e=0.002 m to x_e= 0.022 m, as shown in Figure 20. The expected contact force f_r=300 N, and the output displacement curve of the hydraulic drive unit system when the environmental location changes suddenly can be seen in Figure 21. At 1 s, the contact force disappeared instantly due to the sudden change of the environmental location. Compared with zero virtual damping, when the virtual damping is 20000 and 40000 N·s/m, the hydraulic drive unit system can re-contact the environmental ground stably at a slower speed, and the speed decreases as the virtual damping increases. The virtual damping control proposed in this paper can effectively suppress the occurrence of stall phenomenon and ensure the stability and structural safety of the robot.

Figure 20 Environmental location curve

Figure 21 Displacement output curves with virtual damping

5 Conclusions

1) Considering that the complex environment is unknown and changeable, in this paper, the following methods are used to improve the accuracy and robustness of the contact force tracking control, and maintain the stability and structural safety of the robot. Firstly, an adaptive reference trajectory generation scheme based on Lyapunov function is adopted to realize dynamic contact force control. Secondly, combining backstepping control with sliding mode control, the tracking accuracy and robustness of contact force are improved. When the environment is unchanged, the tracking error of contact force doesn’t exceed 0.1 N; when the environment changes slowly, the tracking error of contact force does not exceed 0.2 N. Finally, by adjusting the input signal of the servo valve, the virtual damping control of the hydraulic drive unit is realized. When the environmental location changes suddenly, the virtual damping characteristic restrains the speed of the drive unit, which makes it re-contact the environment slowly and improves the stability of the robot.

2) The robust force tracking control scheme proposed in this paper has sufficient control accuracy and robustness, and can well meet the control requirements of the hydraulic quadruped robot. But when the speed and acceleration in the interaction process need to be considered, this scheme will lead to force tracking error. Therefore, the next step will carry out dynamic analysis of contact force and try to integrate other advanced intelligent algorithms to improve control performance.

Contributors

SHEN Wei provided the concept and edited the draft of manuscript, LU Xiao-bin conducted the literature review and wrote the first draft of the manuscript and MA Chen-jun edited the draft of manuscript.

Conflict of interest

SHEN Wei, LU Xiao-bin, and MA Chen-jun declare that they have no conflict of interest.

References

[1] KONG Xiang-dong, BA Kai-xian, YU Bin, CAO Yuan, ZHU Qi-xin, ZHAO Hua-long. Force control compensation method with variable load stiffness and damping of the hydraulic drive unit force control system [J]. Chinese Journal of Mechanical Engineering, 2016, 29(3): 454-464. DOI: 10.3901/CJME.2016.0311.030.

[2] SHEN Wei, HUANG Hong-lei, PANG Yu, SU Xiao-yu. Review of the energy saving hydraulic system based on common pressure rail [J]. IEEE Access, 2017, 5: 655-669. DOI: 10.1109/ACCESS.2017.2648642.

[3] SHEN Wei, WANG Jie-hao. An integral terminal sliding mode control scheme for speed control system using a double-variable hydraulic transformer [J]. ISA Transactions, 2019. DOI: 10.1016/j.isatra.2019.08.068.

[4] BOAVENTURA T, BUCHLI J, SEMINI C, CALDWELL D G. Model-based hydraulic impedance control for dynamic robots [J]. IEEE Transactions on Robotics, 2015, 31(6): 1-13. DOI: 10.3929/ethz-a-010604012.

[5] MENDES N, NETO P, PIRES J N, LOUREIRO A. An optimal fuzzy-PI force/motion controller to increase industrial robot autonomy [J]. The International Journal of Advanced Manufacturing Technology, 2013, 68(1-4): 435-441. DOI: 10.1007/s00170-013-4741-3.

[6] DUAN Jin-jun, GAN Ya-hui, CHEN Ming, DAI Xian-zhong. Adaptive variable impedance control for dynamic contact force tracking in uncertain environment [J]. Robotics and Autonomous Systems, 2018, 102: 54-65. DOI: 10.1016/ j.robot.2018.01.009.

[7] SU Xiao-yu. Master–slave control for active suspension systems with hydraulic actuator dynamics [J]. IEEE Access, 2017, 5: 3612-3621. DOI: 10.1109/ACCESS.2017.2672598.

[8] HOGAN N. Impedance control-An approach to manipulation [J]. ASME Transactions Journal of Dynamic Systems & Measurement Control B, 1985, 107(1): 304-313.

[9] MAPLES J A, BECKER J J. Experiments in force control of robotic manipulators [C]// Proceedings of 1986 IEEE International Conference on Robotics and Automation. 1986: 695-702. DOI: 10.1109/ROBOT.1986.1087590.

[10] AREVALO J C, GARCIA E. Impedance control for legged robots: An insight into the concepts involved [J]. IEEE Transactions on Systems, Man and Cybernetics, Part C (Applications and Reviews), 2012, 42(6): 1400-1411. DOI: 10.1109/TSMCC.2012.2187190.

[11] CHEN Ying-hui, ZHAO Jiang-bo, WANG Jun-zheng, LI Duo-yang. Fractional-order impedance control for a wheel-legged robot [C]// Chinese Control and Decision Conference. 2017: 7845-7850. DOI: 10.1109/CCDC.2017. 7978618.

[12] KIM S, KIM J P, RYU J. Adaptive energy-bounding approach for robustly stable interaction control of impedance-controlled industrial robot with uncertain environments [J]. IEEE/ASME Transactions on Mechatronics, 2014, 19(4): 1195-1205. DOI: 10.1109/ TMECH.2013.2276935.

[13] ROVEDA L, IANNACCI N, VICENTINI F, PEDROCCHI N, BRAGHIN F, TOSATTI L M. Optimal impedance force-tracking control design with impact formulation for interaction tasks [J]. IEEE Robotics & Automation Letters, 2016, 1(1): 130-136. DOI: 10.1109/LRA.2015.2508061.

[14] YANG Run-xian, YANG Cheng-guang, CHEN Mou, NA Jing. Adaptive impedance control of robot manipulators based on Q-learning and disturbance observer [J]. Systems Science & Control Engineering, 2017, 5(1): 287-300. DOI: 10.1080/21642583.2017.1347532.

[15] SHENG Xian-jun, ZHANG Xi. Fuzzy adaptive hybrid impedance control for mirror milling system [J]. Mechatronics, 2018, 53: 20-27. DOI: 10.1016/ j.mechatronics.2018.05.008.

[16] LIANG Xiu-quan, ZHAO Huan, LI Xiang-fei, DING Han. Force tracking impedance control with unknown environment via an iterative learning algorithm [J]. Science China, 2018, 62(5): 47-49. DOI: 10.1109/icarm.2018. 8610769.

[17] LIU Hou-de, LU Wei-feng, ZHU Xiao-jun, WANG Xue-qian, LIANG Bin. Force tracking impedance control with moving target [C]// 2017 IEEE International Conference on Robotics and Biomimetics. 2017: 1369-1374. DOI: 10.1109/robio. 2017.8324608.

[18] HE Wei, DONG Yi-ting. Adaptive fuzzy neural network control for a constrained robot using impedance learning [J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(4): 1174-1186. DOI: 10.1109/TNNLS. 2017.2665581.

[19] PENG Jin-zhu, YANG Ze-qi, MA Tian-lei. Position/force tracking impedance control for robotic systems with uncertainties based on adaptive jacobian and neural network [J]. Complexity, 2019, 2019: 1406534. DOI: 10.1155/2019/ 1406534.

[20] KIM T, YOO S K, KIM H S, KI M J. Design and force-tracking impedance control of a 2-DOF wall-cleaning manipulator using disturbance observer and sliding mode control [C]// 2018 IEEE International Conference on Robotics and Automation. 2018: 4079-4084. DOI: 10.1109/icra.2018. 8460897.

[21] ZHANG Xiao-dong, KHAMESEE M B. Adaptive force tracking control of a magnetically navigated microrobot in uncertain environments [J]. IEEE/ASME Transactions on Mechatronics, 2017, 22(4): 1644-1651. DOI: 10.1109/ TMECH.2017.2705523.

[22] SU Xiao-yu, GAO Yan-nan, ZHAO Rui-han. Roll attitude controller design for ships at zero speed [J]. International Journal of Fuzzy Systems, 2018, 20(2): 611-620. DOI: 10.1007/s40815-017-0402-2.

[23] LIN Bin, SU Xiao-yu, LI Xiao-hang. Fuzzy sliding mode control for active suspension system with proportional differential sliding mode observer [J]. Asian Journal of Control, 2019, 21(1): 264-276. DOI: 10.1002/asjc.1882.

[24] SHEN Wei, SU Xiao-yu, PANG Yu, ZHAO Rui-han. Robust controller design for the excavator swing system under the active regulating common pressure rail [J]. Transactions of the Institute of Measurement and Control, 2018, 40(11): 3323-3332. DOI: 10.1177/0142331217707369.

[25] BA Kai-xian, YU Bin, MA Guo-liang, ZHU Qi-xin, GAO Zheng-jie, KONG Xiang-dong. A novel position-based impedance control method for bionic legged robots’ HDU [J]. IEEE Access, 2018, 6: 55680-55692. DOI: 10.1109/access. 2018.2871244.

(Edited by FANG Jing-hua)

中文导读

基于反步滑模和虚拟阻尼的液压四足机器人鲁棒力跟踪控制

摘要：为了提高在不确定和非结构化环境下液压四足机器人的力跟踪性能，采用了基于阻抗的自适应参考轨迹生成方案。然后，为了提高对环境变化的鲁棒性并减少由轨迹跟踪误差引起的接触力误差，将反步滑模控制器与自适应参考轨迹生成器结合使用。最后，提出了一种基于速度和压力反馈的虚拟阻尼控制，以解决环境突然变化引起的接触力消失和失速的问题。仿真结果表明，该方案在环境不变的情况下具有较高的接触力跟踪精度。当环境发生合理变化时，接触力误差始终可以保证在可接受的范围内；当环境突然改变时，驱动单元可以缓慢移动，直到机器人足端重新接触环境。

关键词：液压四足机器人；阻抗控制；反步滑模控制；虚拟阻尼控制

Foundation item: Projects(51975376, 51505289) supported by the National Natural Science Foundation of China; Project(19ZR1435400) supported by the Natural Science Foundation of Shanghai, China

Received date: 2019-12-01; Accepted date: 2020-06-30

Corresponding author: SHEN Wei, PhD, Associate Professor; Tel: +86-21-55270389; E-mail: shenwei@usst.edu.cn; ORCID: https:// orcid.org/0000-0001-9141-9509