J. Cent. South Univ. Technol. (2009) 16: 0112-0118

DOI: 10.1007/s11771-009-0019-1

Seismic response analysis for equatorial diagnostic port plug of international thermonuclear experimental reactor

YU Dong-man(余东满)^{1, 2}, YAO Da-mao(姚达毛)¹, XIE Han(谢 韩)¹, BAO Li-man(鲍立曼)¹, XU Tie-jun(许铁军)¹, PENG Yu-hua(彭玉华)¹, LIU Su-mei(刘素梅)¹, YANG Qing-xi(杨庆喜)¹

(1. Institute of Plasma Physics, Chinese Academy of Sciences, Hefei 200031, China;

2. Department of Mechanical Engineering, Henan Polytechnic Institute, Nanyang 473000, China)

Abstract: Modal analysis and seismic response analysis were carried out for the equatorial diagnostic port plug of international thermonuclear experimental reactor (ITER). The aim of the theoretical analysis is to verify structural strength and reliability of the device. The working condition includes one-dimensional seismic wave and two-dimensional seismic wave. Modal analysis of the device shows that primary vibration is inclined to occur in low-order modes. The horizontal (X-direction, Y-direction) maximum vibration appears at the first and the fourth eigen modes, with the natural frequency of 70.59 and 215.88 Hz respectively, and the vertical (Z-direction) primary vibration appears at the second eigen mode with the natural frequency of 82.85 Hz. According to the results of the finite element analysis (FEA) program, the weak portions of the device are distributed in the joint of port body with blanket shielding module (BSM) and inner side wall of ribbed plate for lifting flange, the maximum von Mises stress is 14.8 MPa with the Y-direction seismic wave. In accordance with the design criteria, the destructive effect is far below the failure boundary, and the structural reliability of the equatorial diagnostic port plug can meet the requirements of the design specifications.

Key words: diagnostic port plug; seismic response; finite element analysis; nuclear fusion

1 Introduction

International thermonuclear experimental reactor (ITER) is one of the largest international cooperative scientific projects for exploring new energy (fusion energy) in the world involving China, European Union, Russia, Japan, USA, Korea, and India[1-4]. As a great project that is just inferior to the International Space Station, ITER will be built as the first large-scale fusion tokamak device and carry out a series of technological experiments to solve some crucial problems. It is a landmark of magnetic controlled nuclear fusion that receives much attention and support from governments and scientists. ITER program is one of the most important projects that China has ever engaged in, which will accelerate the fusion researching process of China and grasp the significant technology of nuclear fusion by participating in the course of design, analysis, manufacture, experiment and operation.

The mission of the ITER is to develop an advanced tokamak experimental device that can produce 500 MW thermal power and will be the first self-sustaining nuclear chain reactor. The plasma discharge current of the device can reach 15 MA, and the reaction time can exceed 16 min. The main frame of the ITER, which is researched and constructed, consists of superconducting magnet system, external vacuum dewar, external and internal cold shield, vacuum vessel and its inner components, magnet feeder system, up-down and equatorial diagnostic port plugs[5-8].

According to the agreements signed by China and ITER Organization, Institute of Plasma Physics, Chinese Academy of Science (ASIPP) has taken on the task of design and manufacture of the No.12 equatorial diagnostic port plug for ITER. Seismic analysis is a key step for the reliability analysis of the nuclear device, and the analysis results can not only verify the structural strength and reliability but also provide some technical data and references for further analysis and optimum design. For example, since 1970 s, a series of medium and small sized tokamak fusion devices, such as HT-6B, HL-1, HT-6M, KT-5 and HT-7[9-12], have been established in China. Based on numerical analysis, different mathematical methods and finite element calculation, seismic analyses have been conducted to compute the dynamic earthquake wave response, and the results are practicably applicable. Therefore, in order to verify structural strength and reliability under the condition of the earthquake destruction, seismic analysis should be carried out in the course of phase design.   All the working behavior parameters in this study were obtained from design tasks or reference documentations offered by ITER Organization.

2 Structure of equatorial port plug

The inner portion (inside of the vacuum vessel) of the equatorial port plug provides vacuum interface for vacuum vessel, inputs all kinds of pilot signals and outputs all kinds of diagnostic signals. The outer portion (outside of vacuum vessel) of the equatorial port plug provides structural support and electromagnetic shield for diagnostic modules and blanket shielding module (BSM)[13-15].

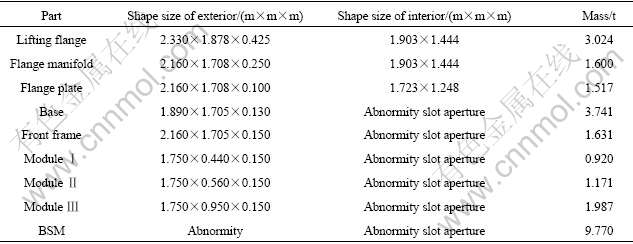
Components of the port plug include lifting flange, flange manifold, flange plate, base, front frame and so on. The visible light diagnostic module and Thomson scattering module are fixed at interior space of port plug. The proposal port plug structure, being fastened with the top lid and keyed by dowels, has a ‘U’ shape, which is available for insertion of the diagnostic modules from the above, as shown in Fig.1. There is an open front frame with the first extending diagnostic module and uncooled rear flange plate. The lifting flange, flange manifold and the gusset plate are welded together, and the trapezoidal section of flange is made of the forged plate with either 1 m in length inner cast waterways or 1 m in length (to be decided) machined and gun-drilled forging. A top plate is made of the sandwich structure machined with the seam plates and spot welded technology. Further details of geometry parameters are listed in Table 1. The main material with the port plug structure is stainless steel (SS) to satisfy the tokamak environment requirements.

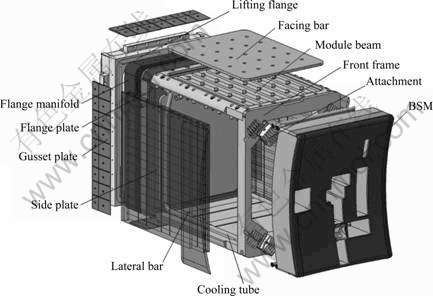
Fig.1 Exploded figure of 3-D model for equatorial port plug

Table 1 Main geometric parameters for parts of port plug

3 Site soil condition and design response spectra(DRS)

ITER is located in the south-east of France on bedrock close to the confluence of Durance and Heron rivers in Provence. After extensive drilling of the Cadarache site loads, ITER Organization has hosen an area with dense limestone up to the natural level to implement the tokamak building and the other building[16-17]. The soil condition used for the analysis of the Cadarache site has been obtained in some reference technology report of ITER Organization, where the assumed shear wave velocity is taken as v_s=1.376 km/s.

Generally, there are two methods for seismic analysis[18-20]. One is the response spectrum method. The spectrum is a curve of response value changing with frequency that represents a response result of a vibrating system. The main response forms are displacement, velocity, acceleration, and force. The other is time-history method that needs complete information about loads variation with time going. However, ITER Organization supplied no time-history information but DRS. Therefore, in this study, the response spectra method was chosen for seismic analysis of the port plug.

For the design of ITER components, two different DRS were selected[16-17]: SMS and PALEO. SMS is a kind of the 5.3-level earthquake event which happened in Manosque in 1905, the projected seismic center is 7.1 km away from Cadarache, the surface acceleration is 3.087 m/s², and the maximum surface acceleration is 7.24 m/s². PALEO is another kind of ancient earthquake event which happened in Cadarache in 1887, the projected seismic center is 18.5 km, the surface acceleration is 2.754 m/s², and the maximum surface acceleration is 6.373 m/s². These spectra are the same in damping coefficient of 5%. They can be compared in Fig.2 with the ASME 0.2 g spectra (issued by American Society of Mechanical Engineers) as required in the generic design. The Cadarache spectra exhibit larger acceleration at frequency above 4 Hz. According to the design specifications of the ITER Organization, at this time, only SMS and PALEO are used for each case to reduce the total amount of the required.

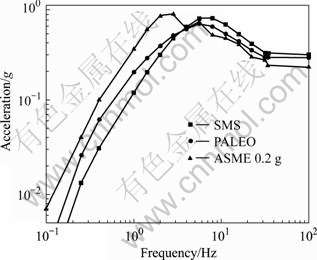
Fig.2 Comparison between ASME DRS for 0.2 g (used before site selection) and two DRSs in Cadarache (all for 5% damping)

4 Procedure of seismic response spectra analysis

The motion differential equation of a system with many freedoms can be described as follows[18-19]:

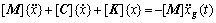           (1)

where  [M], [C] and [K] are the mass matrix, damp matrix, and rigidity matrix, respectively; {x} is the displacement of a point in system; and x_g(t) is the acceleration of the system at specific time.

The decoupling equation of the differential equation can be obtained as:

,

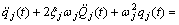
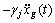j=1, 2, ???, n                                  (2)

where  q_j(t), x_j and, w_j represent the generalized coordinate, fraction of critical damping, and the natural angular frequency of the level-j mode, respectively; and g_j is the modal participation factor of the level-j mode. The generalized coordinate q_j(t) and displacement x_i(t) of the point i can be derived from Eqns.(1) and (2).

Finally, the maximum action F_ji of the seismic surface wave can be calculated as follows:

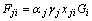                             (3)

where  a_j is the seismic influence coefficient of level-j mode; x_ji is the displacement of level-j mode at the point i; and G_i is the weight of point i in system.

Seismic action effect S_j of the level-j mode can be gotten from the maximum action F_ji. Applying the probability statistics method and superimposing the maximum displacement of the various vibration modal response can get the maximum displacement response. Modal superimposition includes two methods. One is the square root of sum square (SRSS), the other is the complete quadratic combination (CQC). This investigation adopted SRSS for the reason of its widespread application. The total action response (S) of the structural freedom can be gotten through Eqn.(4), where m is the total mode number of the system.

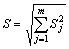                                 (4)

It is evident that the natural frequency and the eigen modal distribution derived from FEA programme are the primary parameters for seismic response spectra analysis. The mass matrix, damp matrix, and rigidity matrix are improved into FEA programme to get the maximum response of port plug. The flowchart of seismic response analysis is shown in Fig.3.

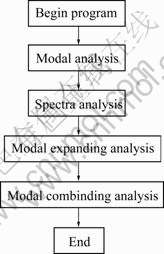
Fig.3 Flowchart of seismic response analysis for port plug

5 Finite element analysis of port plug

5.1 Establishment of port plug model

A simplified finite element model of the port plug, including the BSM, was used for the seismic analysis. The starting point to perform the analysis was a 3D CATIA (V5R11) model of the diagnostic equatorial port plug (some minor details are neglected). This model was imported into ANSYS programme with solid 195 element type. There were 65 880 nodes and 16 681 units being created in the meshed modes. All the freedom degrees of the ribs, inner sides for lifting flange were restricted because they were located at the equatorial neck tube of the vacuum vessel. The structural deadweight was also an important factor, which was applied to the system as an inertial restraint with the acceleration of 9.8 m/s².

5.2 Modal analysis of port plug model

The modal analysis can be used to compute the natural frequency and vibration characteristic of the device. The natural frequency and vibration characteristic are important parameters for the system. First of all, the modal analysis should be carried out before seismic analysis to get the natural frequency and mode characteristic of the port plug. We chose main natural frequencies and mode characteristics from front 10-order modes. The natural frequency and modal distribution are shown in Table 2. The analysis results indicate that the first and fourth eigen modes are horizontal vibration modes, with the natural frequency of 70.59 and 215.88 Hz, respectively, while the second mode is the vertical vibration mode, with the frequency of 82.85 Hz. In other words, the horizontal (X-direction, Y-direction) maximum vibration appears at the fourth and the first eigen modes respectively, the vertical (Z-direction) maximum vibration appears at the second eigen mode, as shown in Fig.4.

Table 2  Natural frequency and mode distribution of front 10-order eigen modes

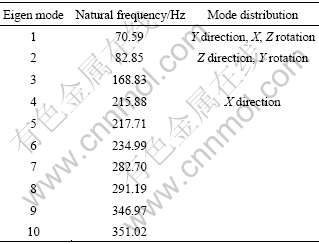
Fig.4 Natural modes for front 4-order eigen modes of port plug model (Deformation range is enlarged): (a) The 1st eigen mode; (b) The 2nd eigen mode; (c) The 3rd eigen mode; (d) The 4th eigen mode

From the above analysis, it can be seen that the vibration response primarily happens in low-order. In most cases, the displacement response of the low-order modes is higher, the acceleration response is lower; while the acceleration response of the high-order modes is higher, the displacement response is lower. At the same time, the low-order modes are inclined to cause structure damage[18]. Therefore, the low-order modes are principal modes for the structural modal vibration and the high-order modes are negligible quantities in this study.

5.3 Seismic response analysis of port plug model

The soil-structure interaction and the interaction with the building were included into the FEA program[17]. The new procedure was supposed to consider the model effective mass and effective height. The detailed model of the building was replaced with the equivalent parallel mass-spring systems.

5.3.1 Seismic analysis under one-dimensional seismic wave

The response spectra of Cadarache were imported into ANSYS programme to find the seismic response in 3D space. One-dimensional seismic spectra were combined with SRSS method to obtain the total response. The von Mises stress and deformation of the system under the Y-direction seismic wave were bigger than those of the X-direction and Z-direction. The detailed information is shown in Fig.5 and listed in Table 3. When the seismic wave was solely applied to Y-direction, by detailed FEA process for the structure of the port plug, the maximum von Mises stress can be found in the joint of port body with BSM and the inner side wall of the ribbed plate for lifting flange, especially in the double- end of the ribbed plate’s inner side wall.

Fig.5 Response results of Y-direction seismic wave: (a) von Mises stress distribution nephogram by SMS seismic wave (unit: Pa);  (b) von Mises stress displacement nephogram by PALEO seismic wave (unit: Pa)

Table 3  Maximum response results under one-dimensional seismic spectra of SMS and PALEO

The maximum von Mises stress is 14.8 and 13.0 MPa, the maximum deformation is 0.489 and 0.431 mm when SMS and PALEO are respectively applied to system. When SMS and PALEO are respectively applied to system in Z-direction, the maximum von Mises stress is 11.4 and 10.1 MPa, the maximum deformation is 0.358 mm and 0.315 mm, which is inferior to that of Y-direction. While the maximum von Mises stress under X-direction seismic wave is just 2.4 and 2.1 MPa, and the maximum deformation is only 0.056 and 0.049 mm. This indicates that the destructive effect of horizontal longitudinal (Y-direction) seismic wave is bigger than that of vertical (Z-direction) seismic wave, while horizontal transversal (X-direction) seismic wave is less than that of vertical (Z-direction) seismic wave.

In this study, ASME, a definite criterion for boiler and pressure vessel issued by American Society of Mechanical Engineers, is suitable for assessing the reliability of port plug. The stress of a system plug can be classified into 3 types: the primary stress, the secondary stress, and the peak stress, according to the criterion of ASMEⅧ-2[21]. Seismic stress is a kind of normal stress or shear stress of the system produced by external applied seismic wave, and belongs to the primary stress (P_m) of the system. Structural discontinuous phenomenon appears at the joint of the plug body with BSM as well as bending stress (Q) produced by deadweight, and seismic loads belong to the secondary stress of the system. According to the third strength theory, the cooperative action of the system loads should meet the following requirements[21]: s_max=P_m+Q<3[σ]. The maximum stress is 14.8 MPa, as shown in Fig.5, the admissible stress [σ] of SS316L is 147 MPa. Therefore, the calculative stress can meet the strength requirements of the device.

5.3.2 Seismic analysis under two-dimensional seismic wave

In the same way, two-dimensional seismic spectra were also combined with SRSS method to obtain the total response. The von Mises stress and deformation of the port plug could also reach the maximum value under the cooperative action of Y-direction and Z-direction seismic waves, The maximum von Mises stress is 13.0 and 11.4 MPa, respectively, the maximum deformation is 0.426 and 0.224 mm, respectively, the detailed information is shown in Table 4 and Fig.6. While the maximum von Mises stress under the cooperative action of X-direction and Z-direction wave is just 8.21 and 7.2 MPa, respectively, and the maximum deformation is only 0.255 and 0.376 mm, respectively. The results prove that the destructive effect of Y-direction plus Z-direction seismic wave is the biggest in all the seismic wave combinations. The maximum stress of the device is 13.0 MPa. The calculative stress can still meet the strength requirement: σ_max=P_m+Q＜3[σ]. Therefore, the port plug can bear the action of two-dimensional seismic wave.

Table 4 Maximum response results under two-dimensional seismic spectra of SMS and PALEO

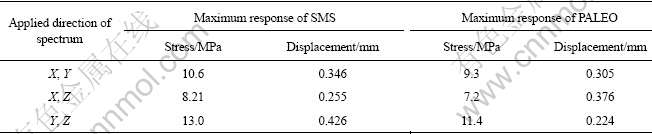
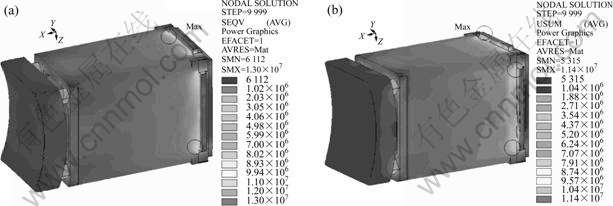
Fig.6 Response results of Y-direction plus Z-direction seismic wave: (a) von Mises stress distribution nephogram by SMS seismic wave (unit: Pa); (b) von Mises stress displacement nephogram by PALEO seismic wave (unit: Pa)

Consideration of the SMS and PALEO seismic wave, both the one-dimensional and two-dimensional working conditions, have the similar weak portions (the maximum response portion), as shown in Figs.5 and 6. The weak portions of the device are distributed in the joint of the port body with BSM and the inner side wall of the ribbed plate for lifting flange, especially in the double-end of the ribbed plate’s inner side wall for lifting flange, which are crucial sites and need for reinforcement or further detailed analysis.

6 Conclusions

(1) The modal analysis of the device shows that the primary vibration is inclined to occur in the low-order modes. The horizontal (X-direction, Y-direction) maximum vibration respectively appears at the first and the fourth eigen modes with the natural frequency of 70.59 and 215.88 Hz, and the vertical (Z-direction) primary vibration appears at the second eigen mode with the natural frequency of 82.85 Hz.

(2) When one-dimensional seismic wave is applied to the system, the destructive effect of the horizontal longitudinal (Y-direction) seismic wave is bigger than that of the vertical (Z-direction) seismic wave, while the horizontal transversal (X-direction) seismic wave is less than that of the vertical (Z-direction) seismic wave.

(3) When two-dimensional seismic wave is applied to the system, the results prove that the destructive effect of Y-direction plus Z-direction seismic wave is the biggest in all the seismic wave combinations.

(4) The weak portions of the device are distributed in the joint of the port body with BSM and the inner side wall of ribbed plate for lifting flange, especially in the double-end of inner side wall of the ribbed plate.

(5) Considering the action conditions of the one-dimensional seismic wave and the two-dimensional seismic wave, the results show that the Y-direction SMS seismic wave can lead to the maximum response, where the maximum von Mises stress is 14.8 MPa, and the maximum deformation is 0.489 mm.

(6) According to the ASME criteria, the destructive effect of seism is far below failure boundary, and the structural reliability of the port plug can meet the requirements of the design specifications.

Acknowledgement

The authors wish to acknowledge all the members who participated in and supported this study. The views and opinions expressed herein do not necessarily reflect those of the ITER Commission.

References

[1] ITER Organization. The ITER design phase [R]. Cadarache: ITER, 2007.

[2] YU Dong-man, XIE Han. Structural design of equatorial diagnostic port plug for ITER [R]. Hefei: ASIPP, 2007.

[3] YU Dong-man, XIE Han. Force analysis of equatorial diagnostic port plug for ITER [R]. Hefei: ASIPP, 2007.

[4] WALKER C. Diagnostic system engineering [R]. Cadarache: ITER, 2005.

[5] WALKER C. Equatorial port plug design-development [R]. Cadarache: ITER, 2005.

[6] WALKER C. Diagnostic port plug loads [R]. Cadarache: ITER, 2004.

[7] DOCEUL L, WALKER C, INGESSON C, CIATTAGLIA E, CHAPPUIS P, PORTAFAIX C, SALASCA S, THOMAS E, TREMBLAY G, BRUYERE C. CEA engineering studies and integration of the ITER diagnostic port plugs [J]. Fusion Engineering and Design, 2007, 82: 1216­­-1223.

[8] WALKER C, BARNSLEY R, COSTLEY A E, GOTTFRIED R, HAIST B, ITAMI K, KONDOH T, LOESSER G D, PALMER J, SUGIE T, TESINI A, VAYAKIS G. ITER diagnostics: Maintenance and commissioning in the hot cell test bed [J]. Fusion Engineering and Design, 2005, 74: 685-690.

[9] YAO Da-mao, SONG Yun-tao, WU Song-tao, HE Ye-xi, WU Wei-yue, DU Shi-jun. Design and structure analyses of HT-7U vacuum vessel [J]. Fusion Engineering and Design, 2001, 58/59: 839-843.

[10] YAO Da-mao, LI Jian-gang, SONG Yu-tao, DU Shi-jun, CHEN Jun-ling, WENG Pei-de. EAST in-vessel components design [J]. Fusion Engineering and Design, 2005, 75/79: 491-494.

[11] YAO Da-mao, SONG Yu-tao, WU Song-tao, WENG Pei-de. HT-7U vacuum vessel [J]. Fusion Engineering and Design, 2003, 69: 355-359.

[12] YAO Da-mao, SONG Yu-tao, DU Shi-jun, WU Wei-yue, WU Song-tao, HE Ye-xi. An optimized structure design of the HT-7U vacuum vessel [J]. Plasma Science and Technology, 2001, 3(4): 865-870.

[13] CIATTAGLIA E, INGESSON L C, CAMPBELL D, SAIBENE G, WALKER C, DOCEUL L, DIRKEN P, PETRIZZI L, HEIDINGER R. ITER diagnostic port plug engineering design analysis in the EU [J]. Fusion Engineering and Design, 2007, 82: 1231-1237.

[14] HONG Y S, KWON T H, AHN H J, KIM Y K, LEE C D. Structural analysis for an upper port of the ITER vacuum vessel [J]. Fusion Engineering and Design, 2007, 82: 1969-1976.

[15] COSTLEY A E, SUGIE T, VAYAKIS G, WALKER C. Technological challenges of ITER diagnostics [J]. Fusion Engineering and Design, 2005, 74: 109-119.

[16] BARABASCHI P, VERRECCHIA M, SORIN V. Summary of soil structure interaction seismic analyses of tokamak building in the candidate sites [R]. Cadarache: ITER, 2003.

[17] GIRARD J P, GR?NTHAL G, NICOLAS M. Design earthquakes for ITER in Europe at Cadarache [J]. Fusion Engineering and Design, 2005, 75/79: 1109-1113.

[18] XU Rong, ZHANG Hui-qiao. Earthquake response spectrum analysis and its application in isolated phase bus [J]. Machine Design and Research, 1999(1): 55-57. (in Chinese)

[19] LIU Hou-xiang, LI Ning, LIAO Xue, WU Cong-shi, PAN Xu-dong. Effective stress analysis method of seismic response for high tailings dam [J]. Journal of Central South University of Technology, 2007, 14(1): 129-134.

[20] YANG Meng-gang, HU Jian-hua, CHEN Zheng-qing. Seismic response analysis of self-anchored suspension bridge with single-tower [J]. Journal of Central South University: Science and Technology, 2005, 36(1): 133-137. (in Chinese)

[21] FAN Qin-shan. Stress analysis and strength design of pressure vessel [M]. Beijing: Atomic Energy Press, 1989. (in Chinese)

Foundation item: Project(10405024) supported by the National Natural Science Foundation of China; Project supported by International Thermonuclear Experimental Reactor Organization in France

Received date: 2008-04-29; Accepted date: 2008-07-24

Corresponding author: YU Dong-man, Doctoral candidate; Tel: +86-551-5593267; E-mail: yudongman@126.com

(Edited by YANG You-ping)