J. Cent. South Univ. Technol. (2011) 18: 1115-1120
DOI: 10.1007/s11771-011-0811-6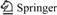
Effects of mask wall angle on matrix-hole shape changes during electrochemical machining by mask
LI Dong-lin(李冬林), ZHU Di(朱荻), LI Han-song(李寒松), LIU Jin-guo(刘金国)
College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics,
Nanjing 210016, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract: The influences of the mask wall angle on the current density distribution, shape of the evolving cavity and machining accuracy were investigated in electrochemical machining (ECM) by mask. A mathematical model was developed to predict the shape evolution during the ECM by mask. The current density distribution is sensitive to mask wall angle. The evolution of cavity is determined by the current density distribution of evolving workpiece surface. The maximum depth is away from the center of holes machined, which leads to the island appearing at the center of cavity for mask wall angles greater than or equal to 90° (β≥90°). The experimental system was established and the simulation results were experimentally verified. The results indicate that the simulation results of cavity shape are consistent with the actual ones. The experiments also show that the repetition accuracy of matrix-hole for β≥90° is higher than that for β<90°. A hole taper is diminished, and the machining accuracy is improved with the mask wall angle increasing.
Key words: electrochemical machining; matrix-hole; machining accuracy; current density distribution
1 Introduction
Many parts involve matrix-hole in the field of aviation, space, automobile, electronics, etc. Therefore, it is important to develop an efficient technique to produce matrix-hole [1-5].
In recent years, there are many methods used to fabricate matrix-hole including micro-drilling, electron beam machining (EBM), ion beam machining (IBM), photochemical machining, laser beam machining (LBM), and electro-discharge machining (EDM) etc. Each of the methods has its own advantage and weakness. Micro- drilling can produce internal stress and burr [6]. LBM can generate a heat affected zone. The process of photochemical machining is poisonous, and the cost is very high for EBM and IBM [7-8]. The tool electrode wear takes place during the EDM [9]. Electrochemical machining (ECM) is an anode dissolution process and has been proved to be a promising machining technique with some advantages such as high machining efficiency, no tool wear, no burr and low production cost [10-11].
ECM by mask involves selective metal dissolution from unprotected areas of mask patterned workpiece in an electrolytic cell. It dissolves the metal workpiece either from a single side or from both sides simultaneously. This technique is employed to fabricate matrix-hole efficiently in extremely hard and tough materials. It offers unique advantages such as short time and low cost because the mask could be re-used. The shape of hole is determined by current density distribution that is affected by mask parameters. These parameters include mask thickness, diameter of hole in the mask and mask wall angle. In this work, the influences of the mask wall angle on the current density distribution, the shape of the evolving cavity and the machining accuracy were investigated.
2 Principle of evolution modeling
The ECM by mask machining system consists of workpiece, insulator, mask and cathode, as shown in Fig.1. The mask locating on the workpiece is movable, not bonded to the workpiece. The mask has matrix-hole pattern which will be transferred to the workpiece. After the desired structure has been obtained, the mask is removed from the workpiece and can be re-used in the later experiments. Electrolyte, which is generally a concentrated salt solution, is pumped out at high speed between the cathode and the mask. The workpiece dissolved electrochemically according to Faraday’s law is flushed away together with generated gas bubbles and Joule heat by the flowing electrolyte. The area of the workpiece exposed in the electrolyte can be dissolved when sufficient voltage is applied.
Fig.1 Schematic diagram of ECM by mask
The workpiece is partially covered by a mask of a certain thickness, e. The pattern involves holes of equal diameter (D) that are separated by a spacing of 2a. The mask wall angle between the mask side wall and the anode workpiece surface is β. The isotropic nature of the workpiece removal process leads to undercut, W. The distance between the cathode and the mask is c. The workpiece thickness is b. The principle diagram of the ECM by mask is shown in Fig.2.
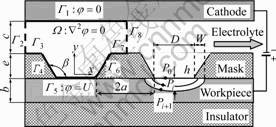
Fig.2 Principle diagram and electric potential distribution of ECM by mask
3 Mathematical model setup and current density distribution
The evolution of cavity is determined by the current density distribution of evolving workpiece surface. Therefore, analysis of current density distribution was carried out. Electric potential distribution and simulation were proceeded to observe the current density distribution [12]. The assumptions are made as follows [13-16].
1) The current density distribution at the workpiece surface is determined solely by the Ohmic effects. Cathode and workpiece are defined as equipotential surface.
2) The rate at which workpiece surface recedes is governed by Faraday’s law.
3) The conductivity of electrolyte, γ, is constant.
The current density distribution is obtained by solving the electric potential distribution as governed by Laplace’s equation within gap domain Ω:
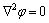(in Ω) (1)
The boundary conditions are
φ|Γ1=0 (at cathode surface) (2)
φ|Γ5=U (at workpiece surface) (3)
φ|Γ2×3×4×6×7×8=0 (under other boundary conditions) (4)
where U is the voltage between the workpiece and the cathode.
The current density, J, is given by
J=γE (5)
The electric field intensity, E, is extracted by the finite element simulation. According to theory of electro- chemical machining, the velocity of workpiece erosion, va, is determined as
va=ηωJ=ηωγE (6)
where ω is the volume electrochemical equivalent value of material, and η is the current efficiency.
As for an initial point (P0) of the workpiece, its coordinates are changed according to the theory of electric field principle. After the time of i?Δt, the point Pi is obtained. Pi+1 is the next point of Pi. The recursion formula is
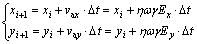(7)
where xi and xi+1 denote the abscissa values of points Pi and Pi+1; yi and yi+1 denote the ordinate values of point Pi and Pi+1. Ex is the point component of the electric field intensity in the abscissa; Ey is the point component of the electric field intensity in the ordinate. In order to describe the current density distribution and the change of the coordinates, the D/2 section is divided into 39 equal parts, and so it has 40 points on the D/2 section. The initial point (P0) locates on the workpiece surface. As the shape evolves, the point Pi moves to the next point Pi+1, as shown in Fig.2. The current density distribution change of points could be achieved by the recursion formula (Eq.(7)).
Finite element method (FEM) is employed to solve the boundary problem of electric field model and to analyze the current density distribution. The shape of evolving cavity is determined by finite element simulation software. The simulation parameters are listed in Table 1. Normalized current density distribution on the initial workpiece surface for various mask wall angles is shown in Fig.3. The normalized current density is defined as J/Jmax where Jmax is the maximum current density on different sections and J is the current density of every key point on different sections.
Table 1 Process parameters used in simulation
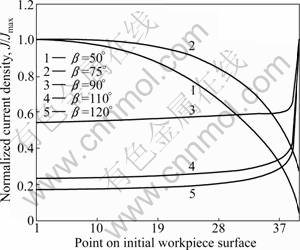
Fig.3 Current density distribution on initial workpiece surface
For β<90°, the maximum current density locates on the center of hole, and it decreases as point approaches mask wall side. Conversely, for β≥90°, the minimum current density lies on the center of hole, and it increases as the point approaches the mask wall side. Therefore, the current density distribution on the initial workpiece surface is extremely sensitive to the mask wall angle. Small changes in the mask wall angle lead to significantly different current density distribution on the workpiece surface, as illustrated in Fig.3. The simulation parameters are the same as Table 1.
The current density distribution on the evolving surface for mask wall angle of 50°, 90° and 120° are plotted as Fig.4. The current density distribution on the workpiece surface shows a maximum at the center of hole and it decreases as the point approaches the mask wall side. This leads to a higher removal rate at the center of the hole compared with the edge during the ECM by mask. Consequently, it is helpful to enhance localization and decrease undercut, as shown in Fig.4(a). Figures 4(b) and (c) show the current density distributions on the evolving surface for β=90° and β=120°. The maximum current density on the initial workpiece surface (t=0 s) locates on the hole wall side. The high current density on the wall side is not desirable since it leads to undercut. However, the undercut results in the redistribution of the current density as the machining proceeds. The maximum current density is transferred to the center of the hole, and the current density on the wall side becomes smaller.
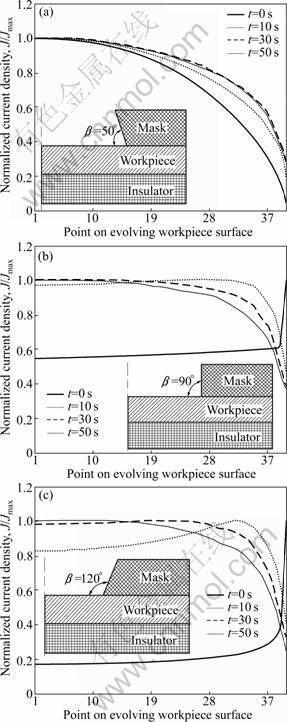
Fig.4 Current density distributions on evolving workpiece surface: (a) β=50°; (b) β=90°; (c) β=120°
4 Experimental
4.1 Setup
The ECM by mask machining system was set up which consisted of electrolyte tank, power supply, and working platform etc, as shown in Fig.5. The workpiece was stainless steel (SS304), which was directly fixed on the insulator placed in a tank. The machining profile of cavity was measured by surface mapping microscope (MicroXAM). The experimental conditions are listed in Table 2.
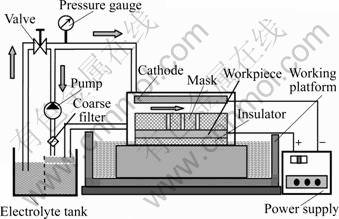
Fig.5 Sketch of ECM by mask machining system
Table 2 Process conditions used in experiment
4.2 Experimental results
4.2.1 Shape of evolving cavity
The simulation parameters are shown in Table 1 and Table 2. Figure 6 illustrates the shape of the evolving workpiece surface for β=50°, 90° and 120° by simulation.
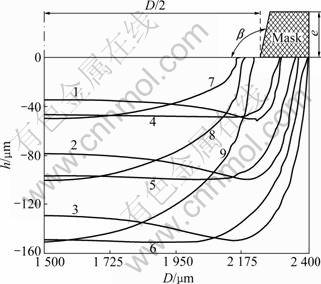
Fig.6 Simulation profiles for ECM by mask: 1—t=10 s, β=120°; 2—t=30 s, β=120°; 3—t=50 s, β=120°; 4—t=10 s, β=90°; 5— t=30 s, β=90°; 6—t=50 s, β=90°; 7—t=10 s, β=50°; 8—t=30 s, β=50°; 9—t=50 s, β=50°
For β=50°, the maximum depth is always at the center of the holes. For β≥90°, the maximum depth is away from the center of the holes as the shape evolves. Figure 6 also shows that the undercut depends on the mask wall angle at the same depth. The undercut for β=50° is less than that for β=90°, which in turn is less than that for β=120°. The machining conditions are the same as the simulation parameters. Experimental profiles for ECM by mask are shown in Fig.7.
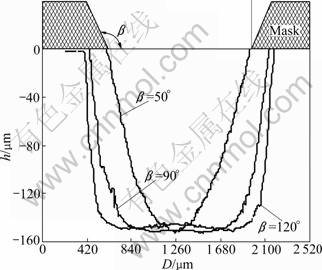
Fig.7 Experimental profiles for ECM by mask
The maximum depth is away from the center of holes machined, which leads to the island appearing at the center of cavity for β≥90°. The undercut of β=50° is obviously less than that for β≥90°. Furthermore, the significant improvement on hole taper is caused by the increase of the mask wall angle. The machining accuracy of β=120° is higher than that for β=50° and β=90°, as shown in Fig.7. The simulation results of cavity shape are well consistent with the experimental results.
4.2.2 Machining accuracy
The improvement on the machining accuracy caused by mask wall angle can be attributed to the electric field distribution localization and electrolyte flow uniformity. It is well known that the uniform and stable electrolyte flow is more easily obtained in the machining gap with the mask wall angle increasing.
One of the most serious problems in ECM by mask is the generation of taper, as shown in Fig.8.
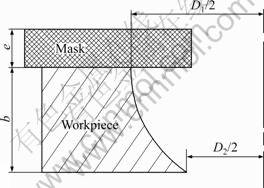
Fig.8 Schematic diagram of hole taper
The hole taper, θ, is determined as
(8)
where D1 is the diameter of entrance, and D2 is the diameter of export. w is the difference in radius of the entrance and the export and is proportional to the hole taper.
Figure 9 shows the change of the hole taper with the hole depth. The results are mean values of the five experiments under the same process parameters and conditions. It is evident from Fig.9 that the hole taper of β=50° is more than that of β≥90°. Hence, the machining accuracy is improved with the increase of β.
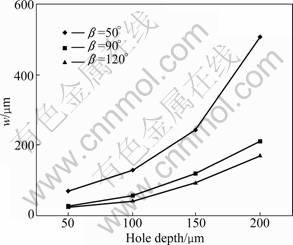
Fig.9 Relation between w and hole depth
The standard deviation S(x) of experimental data is
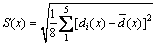(9)
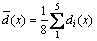(10)
where di(x) is the hole diameter at the measurement point x. The value of standard deviation is a measurement of dispersion extent of machining results. It has a close relationship with repetitive accuracy. The experiment is carried out for four times, and at each time eight holes are selected in the workpiece. Figure 10 shows the standard deviation of different mask wall angle.
Less S(x) means higher repetitive accuracy. This indicates that large mask wall angle leads to less standard deviation, i.e. higher repetitive accuracy. It is clearly shown that the machining fashion for β=50° has a poor repetition accuracy. The deviation is greater than 0.25 mm. The ECM for β≥90° has much better repetition accuracy. Its maximum deviation is less than 0.03 mm, because the harsh electrolyte flow condition causes the deviation. The disturbance in flow condition results in the variation of conductivity and removal rate, which leads to this significant repetition error. In contrast, the ECM for β≥90° shows much better repetition accuracy due to its electrolyte flow field improved.
4.2.3 Matrix-hole machining
The parameters are listed in Table 1 and Table 2. The material of the workpiece is SS304. A series of experiments have been carried out, as shown in Fig.11.
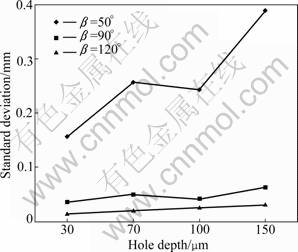
Fig.10 Standard deviation of different mask wall angles
Fig.11 Matrix-holes machined by two-side process of ECM by mask: (a) β=50°; (b) β=90°; (c) β=120°
The three results are caused with the same machining parameters except the mask wall angle. The experimental results shown in Fig.11 strongly indicate that the uniformity of the machined hole and the repetition accuracy are better improved with the mask wall angle increasing. Furthermore, Figure 11(a) shows that the ECM for β=50° has a poor repetition accuracy and the ECM for β≥90° has a much better repetition accuracy due to good electrolyte flow status.
5 Conclusions
1) The current density distribution on the initial workpiece surface is very sensitive to the mask wall angle. During ECM by mask, the shape of evolving cavity causes significant redistribution of the current density on the workpiece surface. As the shape evolves, the current density distribution becomes more uniform with the mask wall angle increasing.
2) The mask wall angle affects the shape of evolving cavity. For β<90°, the maximum etch depth is always at the center of the holes. For β≥90°, the maximum etch depth always departs from the center of the holes, which leads to the island appearing at the center of cavity. The undercut increases with the mask wall angle increasing. The hole taper of cavity profile gradually decreases, and the machining accuracy is improved with the increase of the mask wall angle.
3) The ECM for β≥90° results in a uniform electrolyte flow. Significant improvements in the machining accuracy as well as repetition accuracy are obtained. Good uniformity of diameters of matrix-hole is observed for β≥90°. The uniformity of diameters of matrix-hole machined using mask electrode ECM for β=50° is less than that for β≥90°.
References
[1] SEN M, SHEN H S. Analysis of hole quality characteristics in the electro jet drilling process [J]. International Journal of Machine Tools & Manufacture, 2005, 45 (15): 1706-1716.
[2] LIU Hung-sung, YAN B H, HUANG Fuang-yuan, QIU Kuan-her. A study on the characterization of high nickel alloy micro-holes using micro-EDM and their applications [J]. Journal of Materials Processing Technology, 2005, 169(3): 418-426.
[3] RHIM S H, SON Y K, OH S L. Punching of ultra small size hole array [J]. Annals of the CIRP, 2005, 54(1): 261-264.
[4] LOW D K Y, LI L, CORFE A G, BYRD P J. Spatter-free laser percussion drilling of closely spaced array holes [J]. International Journal of Machine Tools and Manufacture, 2001, 41(3): 361-377.
[5] WANG Ming-huan, ZHU Di. Fabrication of multiple electrodes and their application for micro-holes array in ECM [J]. International Journal of Advanced Manufacturing Technology, 2009, 41(1/2): 42-47.
[6] SUGAWARA A, INAGAKI K. Effect of workpiece structure on burr formation in micro-drilling [J]. Precision Engineering, 1982, 4(1): 9-14.
[7] ROY R, ALLEN D, ZAMORA O. Cost of photochemical machining [J]. Journal of Materials Processing Technology, 2004, 149(10): 460-465.
[8] DUBEY A K, YADAVA V. Laser beam machining—A review [J]. International Journal of Machine Tool & Manufacture, 2008, 48(6): 609-628.
[9] ABBAS N M, SOLOMON D G, BAHARI M F. A review on current research trends in electric discharge machining (EDM) [J]. International Journal of Machine Tool & Manufacture, 2007, 47(7/8): 1214-1228.
[10] RAJURKAR K P, ZHU Di, MCGEOUGH J A, KOZAK J, SILVA A D. New developments in electro-chemical machining [J]. Annals of the CIRP, 1999, 48(2): 567-579.
[11] RYU S H. Micro fabrication by electrochemical process in citric acid electrolyte [J]. Journal of Materials Processing Technology, 2009, 209(6): 2831-2837.
[12] LI Xiang-peng, LI Jie, LAI Yan-qing, CHEN Jiang. Electric field distribution in 75 KA drained aluminum reduction cell [J]. Journal of Central South University of Technology, 2010, 17: 62-67.
[13] SHENOY R V, DATA M, ROMANKIW L T. Investigation of island formation during through-mask electrochemical micromachining [J]. Journal of the Electrochemical Society, 1996, 143(7): 2305-2309.
[14] ZHU Di, QU Ning-song, LI Han-song, ZENG Yong-bin, LI Dong-lin, QIAN Shuang-qing. Electrochemical micromachining of microstructures micro hole and dimple array [J]. Annals of the CIRP, 2009, 58(1): 177-180.
[15] ZHU Di, ZENG Yong-bin. Micro electroforming of high-aspect-ratio metallic microstructures by using a movable mask [J]. Annals of the CIRP, 2008, 57(1): 227-230.
[16] MADORE C, LANDOLT D. Electrochemical micromachining of controlled topographies on titanium for biological applications [J]. Journal of Micromechanics and Microengineering, 1997, 7(4): 270-275.
(Edited by YANG Bing)
Foundation item: Project(50635040) supported by the National Natural Science Foundation of China; Project(2009AA044205) supported by the National High Technology Research and Development Program; Project(BK2008043) supported by the Jiangsu Provincial Natural Science Foundation, China
Received date: 2010-07-07; Accepted date: 2010-10-29
Corresponding author: LI Dong-lin, PhD Candidate; Tel:+86-13913897453; E-mail: ldlnuaa@nuaa.edu.cn
