基于三维热力耦合模型研究不等厚型材在淬火过程中的非均匀冷却行为
来源期刊:中国有色金属学报(英文版)2020年第5期
论文作者:刘志文 易杰 李世康 聂文杰 李落星 王冠
文章页码:1211 - 1226
关键词:铝型材;不等厚壁;水淬;换热系数;热力耦合模型
Key words:aluminum profile; unequal and large thicknesses; water quenching; heat transfer coefficient; thermo- mechanical coupling?model
摘 要:采用反向热传导算法并结合一维末端水淬试验求解热型材与冷却水的界面换热系数。以确定的换热系数作为热边界条件,基于Deform-3D仿真平台建立不等厚壁挤压铝型材在线水淬过程的三维热力耦合模型。系统研究型材水淬过程中的温度场、残余应力场和截面畸变。研究结果表明:随着冷却水流量的增加,界面换热系数增大;高冷却水流量的峰值换热系数出现在低的界面温度;型材淬火过程中横截面上的温度分布严重不均匀,淬火时间为3.49 s时最大温差为300 °C;通过型材横截面不同壁厚部位的温差先急剧增大到峰值,然后逐渐减小;随型材各部位壁厚的增加,温度梯度明显增大;淬火完成后在型材接头内侧和壁厚为10 mm部位的两端存在较大的残余应力;非均匀冷却条件下,型材淬火过程中横截面呈现扭曲型畸变,最大扭曲角为2.78°。
Abstract: The interfacial heat transfer coefficient between hot profile surface and cooling water was determined by using inverse heat conduction model combined with end quenching experiment. Then, a Deform-3D thermo-mechanical?coupling?model for simulating the on-line water quenching of extruded profile with unequal and large thicknesses was developed. The temperature field, residual stress field and distortion of profile during quenching were investigated systematically. The results show that heat transfer coefficient increases as water flow rate increases. The peak heat transfer coefficient with higher water flow rates appears at lower interface temperatures. The temperature distribution across the cross-section of profile during quenching is severe nonuniform and the maximum temperature difference is 300 °C at quenching time of 3.49 s. The temperature difference through the thickness of different parts of profile first increases sharply to a maximum value, and then gradually decreases. The temperature gradient increases obviously with the increase of thickness of parts. After quenching, there exist large residual stresses on the inner side of joints of profile and the two ends of part with thickness of 10 mm. The profile presents a twisting-type distortion across the cross-section under non-uniform cooling and the maximum twisting angle during quenching is 2.78°.
Trans. Nonferrous Met. Soc. China 30(2020) 1211-1226
Zhi-wen LIU1,2, Jie YI2, Shi-kang LI2, Wen-jie NIE1, Luo-xing LI2, Guan WANG3
1. School of Mechanical Engineering, University of South China, Hengyang 421001, China;
2. State Key Laboratory of Advanced Design and Manufacture for Vehicle Body, Hunan University, Changsha 410082, China;
3. College of Mechanical Engineering, Ningxia University, Yinchuan 750021, China
Received 29 September 2019; accepted 18 March 2020
Abstract: The interfacial heat transfer coefficient between hot profile surface and cooling water was determined by using inverse heat conduction model combined with end quenching experiment. Then, a Deform-3D thermo-mechanical coupling model for simulating the on-line water quenching of extruded profile with unequal and large thicknesses was developed. The temperature field, residual stress field and distortion of profile during quenching were investigated systematically. The results show that heat transfer coefficient increases as water flow rate increases. The peak heat transfer coefficient with higher water flow rates appears at lower interface temperatures. The temperature distribution across the cross-section of profile during quenching is severe nonuniform and the maximum temperature difference is 300 °C at quenching time of 3.49 s. The temperature difference through the thickness of different parts of profile first increases sharply to a maximum value, and then gradually decreases. The temperature gradient increases obviously with the increase of thickness of parts. After quenching, there exist large residual stresses on the inner side of joints of profile and the two ends of part with thickness of 10 mm. The profile presents a twisting-type distortion across the cross-section under non-uniform cooling and the maximum twisting angle during quenching is 2.78°.
Key words: aluminum profile; unequal and large thicknesses; water quenching; heat transfer coefficient; thermo- mechanical coupling model
1 Introduction
Aluminum alloys are widely applied in the rail transportation, automotive, aerospace, communication, construction and other industries due to their low density, high specific strength, high stiffness, good corrosion resistance and easy recycling, etc [1-5]. Extruded profiles with large section enable several fabricated classic components to be replaced with an integral construction, and thus the subsequent welding process can be minimized [6,7]. In the predicable future, extruded aluminum profiles will play a more and more vital role in the application of aluminum components [8-11]. Quenching for metal components is a promising heat treatment method to improve the performance of forming products due to its ability of high heat removal rate [12,13]. Quenching aluminum profiles during extrusion press outlet with subsequent aging can increase their strength by 1.5-2 times compared to the as-extruded state. To satisfy the required mechanical properties of profiles, the aluminum alloy billets are usually extruded at a exit temperature above 500 °C (approximately solution temperature), and then are cooled in a cold medium. The quenching process is generally carried out either by putting the components into water or by spraying them with fluids [14,15]. The on-line water quenching after extrusion, compared with other quenching techniques, has higher heat fluxes, heat transfer efficiency and low energy consumption, which is widely used in aluminum profile quenching [16-18]. For the extruded profiles with a large section, multiple nozzles need to be arranged reasonably on the outer surface of profile in the quenching system, and suitable water flow velocities should be afforded. Otherwise, it maybe leads to a non-uniform cooling and large residual stress in quenched profiles. Good control for water flow velocities will obtain better results of solid solution treatment for extruded profiles and it will be also helpful to control the profile distortion. It is very important to predict the temperature evolution, residual stress and distortion of profile during on-line quenching process.
Due to the fact that the quenching process of profile is a typical problem of thermo-mechanical coupling, it is practically impossible to predict accurately the quenching process by simply using the theoretical analysis or experiment methods. In this case, numerical simulation is of use in investigating the on-line quenching process and obtaining necessary physical quantities, such as temperature, residual stress and deformation [19-21]. In recent years, with the help of numerical simulations, many researches have been carried out with respect to the analyses of temperature field, residual stress field and shape distortion in quenching. YANG et al [22] simulated the flow distribution in quench tank for heat treatment of large complicated aluminum components using Fluent computational fluid dynamics software. The flow velocity and the uniformity of flow field in two types of quench tanks with or without agitation system were calculated. WANG et al [23] analyzed the temperature and stress distributions of a circular pipe during on-line quenching process by using finite element (FE) simulation combined with experimental methods. YANG et al [24] investigated the quenching process of large complicated thin-wall workpiece by FE simulation. The maximum residual stress and distortion of quenched workpiece under different quenchants and quenching temperatures were predicted. NOWAK et al [25] studied the influence of the technological spray cooling parameters on the final profile temperature and on the resulting mechanical properties of EN AW-6082 aluminum profile. BIKASS et al [26] revealed the distortion mechanism due to non-uniform cooling in the aluminum extrusion process. The effect of the non-uniformity ratio, width ratio, thickness and width of the section on the shape distortion were studied. They also investigated the effect of the initial cooling rate on the distortion mechanism due to nonuniform cooling throughout the thickness by introducing a parameter called “the front width” [27]. EDELBAUER et al [28] developed an Eulerian spray model for simulations of spray quenching and cooling in water mist chambers. To validate the model, measurements of the temperature history at certain locations within a quenched test geometry have been performed and compared with the numerically predicted results. FENG et al [29] developed a FE model to predict the residual stress after quenching process by quenching aluminum blocks with different thicknesses into water and polyalkylene glycol solution. The influences of block thickness and quenchants on residual stresses were investigated. Heat transfer coefficient is the most decisive factor in influencing the quenching results, compared with other data such as material properties, process parameter and other conditions. In the FE model, heat transfer coefficient needs to be used to calculate the heat exchange between the hot profile surface and quenchant. Therefore, in order to accurately simulate the quenching process and predict the temperature field of extruded profiles, the quantitative determination of heat transfer coefficient at different water flow rates will be very valuable. GOLOVKO et al [30] identified the heat transfer coefficients of 6082 aluminium alloy sheets during spray cooling based on the measured surface temperatures and by applying a lumped heat capacitance method. GUO et al [31] investigated the effect of water temperature and nozzle pressure on the heat transfer coefficient during spray quenching for 2024 aluminum alloy thin sheets.
According to the above references, many researches focused on the FE simulations of on-line quenching process for aluminum alloy have been carried out. However, the research objects were mainly focused on the aluminum sheets or simple profiles with thin thickness. Little research has been reported on the water quenching process of extruded profile with unequal and large thicknesses. In this work, the study combining simulation analysis with experimental method was performed to investigate the water quenching of extruded aluminum profile with a large section and unequal thicknesses and to predict the temperature, residual stress and distortion evolution. Cooling curves of 6082 aluminum alloy under different water flow rates were obtained by end quenching experiment, and the interfacial heat transfer coefficients between the hot profile surface and cooling water were identified by using inverse heat conduction method. Using the identified heat transfer coefficient as the thermal boundary condition, a three-dimensional thermo-mechanical coupling model of water quenching process for extruded profile was established in the Deform-3D software platform. The accuracy of FE model was validated by the comparison of measured and simulated temperatures on the outer surface of profile. The temperature field, residual stress field and distortion of profile during quenching were investigated and analyzed systematically. This study will provide effective theoretical guidance for revealing the heat transfer behavior and the distortion mechanism in water quenching of complex aluminum profile.
2 Identification of heat transfer coefficient during water quenching
2.1 End quenching experiments
The heat transfer coefficient between the hot profile surface and cooling water is an important parameter for establishing the thermal boundary conditions in numerical simulation of on-line water quenching of extruded profile, which directly affects the calculation accuracy of temperature field, residual stress field and distortion of profile. In this study, method in end quenching experiments combined with inverse heat conduction was utilized to determine the heat transfer coefficients at different water flow rates. The material used in this study was a commercial 6082 aluminum alloy. The chemical composition is shown in Table 1. The quenching samples were taken from a natural aging extruded bar with a diameter of 32 mm. The schematic diagram of end quenching set-up in the experiment is shown in Fig. 1. It consists of water spray quenching system, specimen and data acquisition system. A tank containing cooling water was placed in the bottom of the device. The cooling water was pumped by a pump and water pipe. The room temperature water used as a cooling medium during the tests can be reused. A flowmeter and control valve were installed in the middle of the pump and nozzle in order to adjust the spray water flow rate as needed. The nozzle shape was round with a diameter of 10 mm and the distance from the outlet of nozzle to the surface of sample was 80 mm.
Table 1 Chemical composition of 6082 aluminum alloy (wt.%)


Fig. 1 Schematic diagram of end quenching experimental set-up

Fig. 2 Schematic diagram of quenching sample and thermocouples layout (unit: mm)
Cylindrical samples were used to equivalently study the interaction between extruded profile and cooling water during quenching. Figure 2 shows the dimensions of quenching sample and the location of thermocouples. All samples were machined into the size of d30 mm × 125 mm. The surface roughness of samples was 0.5 μm which was in accordance with the actual surface roughness of the extruded profile. Aiming to measure the temperature evolution, three K-type thermocouples labeled by T1, T2 and T3 with the diameter of 3 mm were centrally positioned on the lateral surface of each sample. The distances between the quenching surface and the three thermocouples are 3, 10 and 20 mm, respectively. A screw hole with a diameter of 6 mm and depth of 15 mm was designed on the upper surface of specimens to fix the sample. The side surface of the samples was wrapped with an asbestos layer tighten by aluminum foil, to ensure that the water flow only contacts the bottom end of the specimen. Thus, the heat transfer behavior between the cooling water and sample can be approximated as one-dimensional heat transfer. The samples were heated to 500 °C and soaked for 3 h in the electric resistance furnace, and then quickly transferred to the operating position within 10 s. NI USB 9213 data acquisition instrument was used to collect temperature data at a rate of 100 Hz, which consists of a 16 channel, 24 bit data acquisition instrument with a sampling rate of 1200 samples per second. The uncertainty of temperature measurement is less than 0.25 °C for the K-type thermocouple, while the uncertainty of the placement of thermocouples is estimated to be ±0.2 mm. The interfacial heat transfer coefficient between the samples and cooling water was determined by using the inverse heat conduction program based on the measured temperature data.
2.2 Inverse heat conduction model
There are many factors such as material properties, quenching media, water flow rate and surface roughness, which can influence the heat transfer coefficient. Thus, quantitative identification of the heat transfer coefficient through simple mathematical model is still very difficult. In this study, method in inverse heat conduction combined with quenching experiment was used to determine the heat transfer coefficient between the hot profile surface and cooling water. As shown in Fig. 1, the quenching process can be approximately considered as an one-dimensional heat transfer, thus the transient heat conduction equation can be defined as follows:
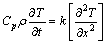 (1)
(1)
where Cp, ρ and k are the specific heat, density and the thermal conductivity of sample; T is the temperature sample; t is the time.
The inverse heat conduction equations were executed by adopting an iterative approach. To ensure that the program can execute and satisfy the required solution accuracy, optimization model and convergence criterion were needed to establish. The norm of difference between the measured and calculated temperatures at each iteration was used as the convergence criterion S(h), which can be written as follows [32]:
 (2)
(2)
where  is the measured temperature changing with time ti(i=1,…, Nt) at the location of xj(j=1,…, Nm);
is the measured temperature changing with time ti(i=1,…, Nt) at the location of xj(j=1,…, Nm); 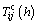 is the corresponding calculated temperature; h is the unknown interfacial heat transfer coefficient, h={h1, h2, …, hNh}, Nh is the number of heat transfer coefficients required solution; σT is the error of measured temperature; σk is the allowable maximum variation of h at each iteration; and
is the corresponding calculated temperature; h is the unknown interfacial heat transfer coefficient, h={h1, h2, …, hNh}, Nh is the number of heat transfer coefficients required solution; σT is the error of measured temperature; σk is the allowable maximum variation of h at each iteration; and 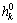 is the hypothetical initial heat transfer coefficient.
is the hypothetical initial heat transfer coefficient.
To calculate the interfacial heat transfer coefficient h, the minimum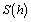 is required, thus there is [33]
is required, thus there is [33]
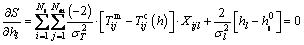 (3)
(3)
where Xijl is the sensitivity coefficient, which can be linearly expanded with the Taylor formula at the heat transfer coefficient :
:
 (4)
(4)
The δhl is the variation of hl at previous iteration, which is used to calculate the sensitivity coefficient Xijl. In the calculation process of temperature field, the temperature of the next iteration  is also linearized, that is,
is also linearized, that is,
 (5)
(5)
where the variation of heat transfer coefficient is calculated by the following equations:
is calculated by the following equations:
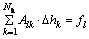 (6)
(6)
 (7)
(7)
 (8)
(8)
The reverse solution process of heat transfer coefficient during quenching is described in detail as follows.
(1) The temperature data of three locations (T1-T3) inside the sample changing with time were obtained by the end quenching experiments.
(2) Assume that the initial heat transfer coefficient  , and a maximum iteration number of M was set. Before entering some iteration, the advanced algorithm compared the number of this iteration with the maximum value.
, and a maximum iteration number of M was set. Before entering some iteration, the advanced algorithm compared the number of this iteration with the maximum value.
(3) The temperature field  of the sample was calculated by numerical simulation.
of the sample was calculated by numerical simulation.
(4) The sensitivity coefficient Xijl was calculated by Eq. (4).
(5) Through Eqs. (6)-(8), the variation of heat transfer coefficient is obtained. If |Δhk/hk|<ε, the calculation is terminated, and the heat transfer coefficient is output, otherwise, the heat transfer coefficient  , and the program is gone to the third step.
, and the program is gone to the third step.
During reverse operation process, it is necessary to calculate (Nh+1)M times for the forward solution of temperature fields, which inevitably consumes a large amount of computing time. Therefore, the one dimensional end quenching experiments adopted in this study can shorten the computation time of forward solution and improve the efficiency of inverse operation. The transient temperature field of samples during the end quenching was solved by FE method. Figure 3 shows the calculation flow chart of inverse heat conduction algorithm.

Fig. 3 Calculation flow chart of inverse heat conduction algorithm
2.3 Determination of heat transfer coefficients
Figure 4 shows the measured cooling curves at the location of 10 mm from the sample surface with different water flow rates. It is clear that the general shape of the 5 sets of cooling curves is similar. There are two stages in the cooling curves: rapid decline stage and slow decline stage. The temperatures decrease rapidly in the rapid decline stage (0-20 s), then continue to decrease slowly. At the initial 10 s of quenching, the temperatures decrease sharply due to the large difference of interface temperature between the profile surface and cooling water, and the 5 sets of cooling curves are basically in coincidence. After quenching for 10 s, the cooling rate increases obviously as water flow rate increases. This can be attributed to that, the cooling water is able to fill into micro-cavities of sample surface deeply as the water flow rate increases, thus the contact heat transfer area and heat flux increase. After quenching for 20 s, the cooling rates for the water flow rates of 0.30 and 0.40 m3/h are relatively small. However, the temperature at the water flow rate more than 0.55 m3/h continues to drop until the time reaches 100 s, then keeps stable.

Fig. 4 Cooling curves at location of 10 mm from sample interface with different water flow rates
Figure 5 shows the variation of calculated heat transfer coefficient with interface temperature at different water flow rates. It can be seen that the heat transfer coefficient and the interface temperature were evidently non-linear relation. The five curves present the similar tendency. The heat transfer coefficient first increases linearly with the decrease of interface temperature, then reaches the peak value at the interface temperature of 108-180 °C due to both vigorous boiling and full fluid contact. After reaching the peak value, heat transfer coefficient decreases rapidly as the interface temperature decreases. The heat transfer coefficient increases with increasing water flow rate. The peak heat transfer coefficient is 15.7074 kW/(m2·°C) at the water flow rate of 0.30 m3/h and surface temperature 180 °C. In addition, the peak heat transfer coefficient with higher water flow rates appears at lower interface temperatures. When the water flow rate increases to 1.00 m3/h, the peak heat transfer coefficient increases to 34.795 kW/(m2·°C), increasing by 122.7% compared with that at 0.30 m3/h. The interface temperature corresponding the peak heat transfer coefficient drops to about 108 °C. Higher water flow rate corresponds to greater total water flow volume. The increase of total water flow volume can not only increase the bubble evaporation heat transfer, but also increase the single-phase heat transfer. The greater single-phase convection heat transfer is able to decrease the decline of heat flux. Thus, the peak heat transfer coefficient with higher water flow rates appears at lower interface temperatures. It can be also seen from Fig. 5 that the difference of heat transfer coefficient when the water flow rate varies from 0.30 to 0.70 m3/h is larger than that when the spray pressure varies from 0.70 to 1.00 m3/h. With the increase of water flow rate, the cooling water can be filled into micro-cavities deeply, and the heat transfer area increases. However, the fluid surface tension and entrapped air pressure, hindering the fluid filling into the micro-cavities, also increase with the increasing water flow rate. At low water flow rate, each unit increment of water flow rate will lead to the increase of the heat transfer area and heat flux due to the smaller fluid surface tension and entrapped air pressure. However, at high water flow rate, each unit increment of water flow rate causes less increase in the heat transfer area due to the increasing fluid surface tension and entrapped air pressure. Heat transfer coefficient is an important thermal boundary condition for the accurate simulation of heat transfer during water quenching. Thus, the identified heat transfer coefficient at different water flow rates provides a theoretical basis for the determination of the heat transfer boundary conditions in the numerical simulations of the on-line quenching process of extruded profile.
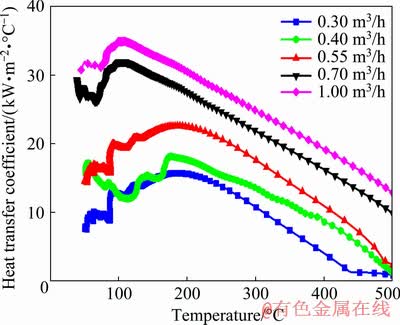
Fig. 5 Variation of calculated heat transfer coefficient with interface temperature at different water flow rates
3 Thermo-mechanical coupling model for simulating water quenching
3.1 Quenching scheme description for extruded profile
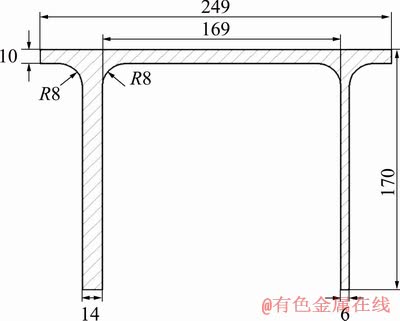
Fig. 6 Shape and dimensions of extruded aluminum profile (unit: mm)
The research object in this study was a 6082 extruded profile with π-shaped section used in urban rail traffic, which had a maximum width of 249 mm and height of 170 mm, as shown in Fig. 6. In addition, the wall thicknesses of the three parts of profile were severe non-uniform, and the thicknesses were 6, 10 and 14 mm, respectively. The water spray quenching experiments were performed using a multi-nozzles spray cooling system integrated into the 4000 t extrusion press. The extrusion process conditions and parameters were selected to be similar to the real process in plants. Table 2 shows the detailed conditions of the extrusion process. Due to the high-quenching sensitivity properties of 6082 alloy, the large section dimension and wall thickness difference, the required quenching method is able to provide enough cooling strength for extruded profiles to ensure better mechanical properties after aging and minimum distortion of profiles. The cooling rate for air quenching is low and the profile is prone to distort, thus the water quenching is adopted for this profile. Figure 7 shows the schematic configuration of the spray cooling device and applied nozzle positions. The cooling device was installed at a distance of about 1000 mm from the front plate of press. Multi-row spray nozzles were arranged on the outer surface of profile in order to ensure temperature uniformity over the profile cross- section on leaving the spray cooling device. The direction, distance, velocity of the nozzles can be automatically controlled by the computer according to the material, shape and dimension of the extruded profiles. The shape of the actual nozzles in quenching device was fan-shaped. In this study, the water flow rates of all nozzles are 0.30 m3/h.
3.2 Thermo-mechanical coupling model
3.2.1 FE mesh modelling
The 3D thermo-mechanical model for simulating the on-line water quenching of aluminum extruded profile was established based on the Deform-3D software using coupled thermal- displacement analysis. Figure 8 shows the thermo- mechanical coupling model of on-line water quenching. In order to improve the simulation accuracy and save computer source, the quenching and non-quenching regions were allocated for different mesh sizes. The model lengths in the quenching box, near the die side and the puller side are 1000, 2000, 100 mm, respectively. The hexahedra element was adopted for meshing the extruded profiles, the region in the quenching box was meshed with higher element density and finer elements. At least three nodes were assigned in the thinnest position of cross section profile, and the element size was about 1/2 of the minimum wall thickness of profile. However, in the non-quenching region, the mesh size along the profile length was set to be about 20 mm. After meshing, the element size and quality need to meet the following basic conditions: (1) the minimum element size >0.1 mm; (2) the length-to-width ratio of tri-prism element <12; (3) the minimum angle of element >15°, the maximum angle of element <165°; (4) Jacobian >0.7. The total numbers of elements and nodes of the FE model were 35283 and 48610, respectively. By checking, the mesh quality of all elements meets the above requirements.
Table 2 Experimental extrusion parameters

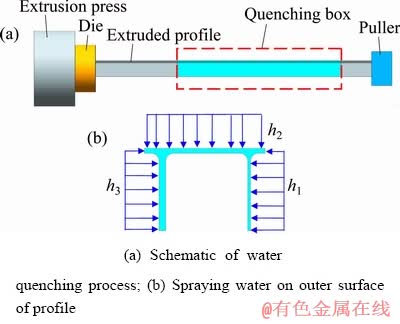
Fig. 7 Experimental principle of on-line quenching process for extruded profiles

Fig. 8 Thermo-mechanical model of on-line water quenching process
3.2.2 Mathematical models
The heat conduction equation describes the heat distribution over time at given regions. The elastic-plastic material model was adopted in the FE simulation. According to the Fourier model and the first law of thermodynamics, the equation for calculating the temperature distribution of extruded profiles is described as
 (9)
(9)
where ρ, c and λ are the density of profile, specific heat, and thermal conductivity, respectively; T and t are temperature and time, respectively; qv is the latent heat of phase transformation, and the value is set to be zero due to the inhibition of secondary phase Mg2Si precipitation during quenching.
For the coupled temperature-displacement systems Deform-3D solves a system shown as follows:
 (10)
(10)
where Δu and ΔT are corrections to the incremental displacement and temperature, respectively; Kuu, KuT, KTu and KTT are the sub-matrices of the coupled stiffness matrices; Ru and RT are the thermal residual vectors, respectively. These systems are solved simultaneously using the Newton’s method. The initial stress of extruded profiles was assumed to be 0 MPa.
3.2.3 Boundary conditions
In the two ends of profile along the extrusion direction, the mechanical boundary conditions (constraints) were defined to represent the roles of the extrusion die and puller. At the extrusion die end, profile’s edge was fixed while at the puller side, the profile was constrained only in the middle part (see Fig. 8).
Generally, thermal boundary condition is defined as
 (11)
(11)
where n is normal direction of the sprayed surface of profile; h is the convection heat transfer coefficient between the cooling medium and profile surface; T and T0 are the temperature of profile surface and medium temperature, respectively. In this study, the water flow rates of all nozzles arranged on the outer surface of profile are all 0.30 m3/h, thus the heat transfer coefficients h1, h2 and h3 on the outer surface of the three parts of profile in the region of quenching box are identical (see Fig. 7(b)). In FE simulation, the heat boundary conditions between the profile surface and cooling water were established respectively based on the identified heat transfer coefficients by inverse heat conduction method. Thus, the corresponding heat transfer coefficient at the water flow rate of 0.30 m3/h was directly used as an input date of thermal boundary condition. Besides, the convection heat transfer coefficient between the environment and profile surface was set to be 100 W/(m2·°C).
The initial condition is an initial value problem. In this study, initial condition is the exit temperature of extruded profile from the extrusion die. The equation of initial condition at time t=0 is described as
 (12)
(12)
where T0(x, y, z) is the initial temperature function. Since the heat transfer along the extrusion direction is very small, assuming that both end surfaces of the profile are adiabatic. The extrusion exit temperature of 500 °C was defined for the extruded profile, which is regarded as a uniform temperature field. The initial temperature of the cooling water was 27 °C.
During water quenching, there are great differences for the thermophysical parameters of material such as thermal conductivity and specific heat capacity at different temperatures. To improve the simulation precision, it is necessary to be accurately measured. Figure 9 shows the thermal conductivity and specific heat capacity of 6082 aluminum alloy at different temperatures. It can be seen that the thermal conductivity and specific heat capacity increase with increasing temperature. When the temperature is 500 °C, the thermal conductivity and specific heat capacity increase by 9.71% and 22.55%, respectively relative to those at room temperature.

Fig. 9 Thermal conductivity and specific heat capacity of 6082 aluminum alloy
After FE modeling, the on-line water quenching process of extruded profile was simulated and the simulation time was about 12 h in the ThinkStation C30 workstation. Then, a series of simulated results such as the temperature field, residual stress field and distortion of profile, can be obtained. To validate the thermo-mechanical coupling model and quantitatively reveal the variation of physical quantity, locations of A1-C2 (see Fig. 10) at the centre positions of three parts of profile with unequal thicknesses and locations of D-I at the joint and the ends of three parts of profile were selected to analyze.
3.3 Experimental verification
The temperature field is the basis of calculating thermal stress and residual deformation of extruded profiles during quenching, which is easy to realize the real-time and on-site measurement compared to the other physical quantities. Thus, temperature field is used to validate the reliability of the thermo-mechanical coupling model. Extrusion experiment of aluminum profile was carried out on the 4000 t extrusion press and experimental conditions are presented in Table 2. The exit temperature of extruded profile was controlled at about 500 °C. When the billet extruded through the die bearing, then was directly taken into the on-line water quenching device arranged in the exit of extrusion press. The temperatures of the outer surface of extruded profile at the locations of A1 and C1 were measured using the contactless infrared thermometers which are respectively arranged at the locations of 0.25, 0.5 and 1 m from the entrance of the quenching device. The corresponding quenching time for the measured locations in the FE simulation is 2.5, 5 and 10 s, respectively. Figure 11 shows the comparison of the simulated and measured temperatures at the locations of A1 and C1. It is clear that the trends of temperature curves of the simulated and measured results in general are consistent. The maximum relative errors of the calculated and measured temperatures at the locations of A1 and C1 are 12% and 5.6%, respectively. The slight difference is mainly due to the poor repeatability of the experiment and uncertainty. Some uncertainties existed in addition to general differences between the FE simulation and experiment. The cooling of the outer surface of extruded profile by the water spraying in the simulated model is stable, while for the experiment, the distribution of the water spraying varied at every trial. The prediction error is well within the range of that deemed to be accepted, which indicates that the established thermo-mechanical coupling model is accurate and can be used to simulate the water quenching process of extruded profiles.

Fig. 10 Locations on middle section of profile selected to quantitatively investigate physical quantity of quenching process
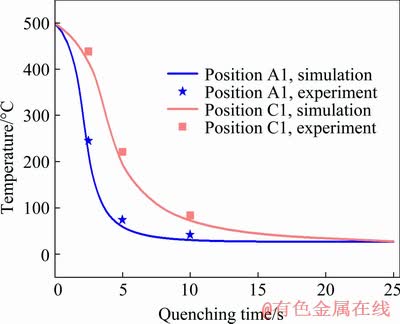
Fig. 11 Comparison of simulated and measured temperatures at locations of A1 and C1
4 FE analysis of water quenching process for extruded profile
4.1 Temperature evolution during water quenching

Fig. 12 Temperature distributions of extruded profile in quenching box at different quenching time
The variation of temperature field reflects the heat transfer between the hot profile and cooling water, which is also the theoretical basis for the calculation of residual stress and distortion of profile. To reveal the temperature evolution of profile during quenching, the temperature field results at the quenching time of 1, 2.5, 5, 7.5, 15 and 20 s were extracted to analyze. Figure 12 shows the temperature distributions of profile during quenching at different quenching time. It can be seen that from Fig. 12(a), at the beginning of quenching (1 s), the temperature on the outer surface of profile drops rapidly due to the severe heat exchange with the cooling water. The minimum temperature of profile is 452 °C, which is located on the outer surface of the part with the thickness of 6 mm. However, the temperature of the inner surface of the part with the thickness of 14 mm is slightly deceased to 494 °C owing to the low heat transfer with surrounding environment. As can be shown in Fig. 12(b), after 2.5 s of quenching time, the temperature distribution on the cross- section of profile is extremely nonuniform. The maximum temperature difference of profile reaches 261 °C. The temperature in the part with thickness of 6 mm decreases sharply to 200 °C, while that in the other parts is high than 400 °C. As seen in Fig. 12(c), after 5 s of quenching time, the temperature difference of profile is still very large and the maximum value is 234.6 °C. As can be shown in Fig. 12(d), at quenching time of 7.5 s, the cooling rate in the part with thickness of 14 mm is obviously increased, and the maximum temperature is decreased to 150 °C. As can be seen in Fig. 12(e), the maximum temperature difference of profile is further reduced to 29.8 °C. After 20 s of quenching (see Fig. 12(f)), the temperature difference of profile is very small and at this time, the quenching process is considered as a finished state.
In order to quantitatively analyze the temperature evolution of three parts of profile with different thicknesses during quenching, the cooling curves of locations A1-C2 (see Fig. 10) on the cross-section of profile were extracted, as shown in Fig. 13. It is clear that the general trend in the data is similar for all locations in that there is an initial rapid drop in temperature at the initial quenching stage, which is followed by a relatively slow rate of decrease. Finally, the temperatures decrease to a constant which is same as the cooling water temperature of 27 °C. The cooling rates of locations A1 and A2 are significantly larger than those at the other locations. The lowest cooling rates are located at the locations of C1 and C2 in the part with thickness of 14 mm. The reason is that the locations on the outer surface of profile not only dissipates the heat away to the cooling water, but also absorbs the heat from the surrounding. The absorbed heat fluxes with large thicknesses are higher than those with low thicknesses. This results in the slow decreasing of temperature. In the later stage of quenching (after about 15 s), the absorbed heat flux in comparison with the heat loss with cooling water can be negligible, thus the cooling rates of all locations are basically identical. It can be also seen from Fig. 13 that there exists obvious temperature gradient through the thickness of the three parts of profile. Figure 14 shows the variation of temperature difference through the thickness in different parts of profile during quenching. It is clear that when cooling occurs through the thickness, which is severe non-uniform for the three parts of profile. The temperature difference through the thickness first increases sharply to a maximum value, and then decreases gradually. The quenching time for the arrival of the maximum temperature difference in the three parts of profile is 2.33, 3.43 and 3.35 s, respectively. Moreover, the temperature gradient increases obviously with the increase of part thickness. The maximum temperature difference in the part with thickness of 14 mm is up to 210 °C, which is 167.2 °C larger than that in the part with thickness of 6 mm. Figure 15 shows the maximum temperature difference across the cross-section of profile during quenching. It is clear that the maximum temperature difference is 300 °C at the quenching time of 3.49 s. The large temperature difference is mainly due to the non-uniform cooling of different parts of profile and higher cooling rate on the outer surface than that on the inner surface.

Fig. 13 Cooling curves of locations A1-C2 on cross- section of profile during quenching
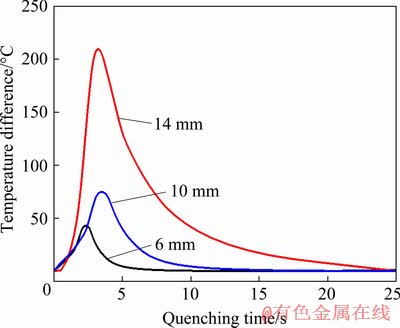
Fig. 14 Typical temperature difference through thickness of three parts of profile during quenching

Fig. 15 Maximum temperature difference across cross- section of profile during quenching
4.2 Stress evolution during water quenching
During quenching, there exist transformation and thermal stress in the interior of profile. The former is caused by the non-uniformity of phase transformation of the material, while the latter is caused by the inconsistent shrinkage rate of different parts of profile. Since the phase transformation has almost no effect on aluminum alloy, this study only considers the thermal stress caused by the non-uniform cooling of profile. Figure 16(a) shows the thermal stress evolution of locations A1-C2 in the three parts with different thicknesses during quenching process. It is clear that the principal stresses of locations A1 and A2 in the part with the thickness of 6 mm are both tensile stress. The principal stresses show a similar tendency, that is, the tensile stress rapidly increases to the peak value, then decreases to a lower one. In addition, the stress magnitude of location A1 is large at the initial quenching stage, while lower at the later stage of quenching than that of location A2. For the part with the thicknesses of 10 mm, the outer and inner surfaces before 4.53 s suffer tensile and compressive stresses, respectively (see the curves of locations B1 and B2). After quenching for 4.53 s, the stress state of inner surface is changed to tensile stress and the stress magnitude is larger than that of the outer surface. The stress state for the part with the thicknesses of 14 mm before 8.23 s is also tensile-compressive stresses (see the curves of locations C1 and C2). Moreover, the stress magnitude and gradient along the thickness in the region with the thicknesses of 14 mm is obviously larger than that in the region with the thicknesses of 10 mm. This is mainly due to a higher temperature gradient through the thickness in comparison with the other two parts. Figure 16(b) shows the stress evolution of locations D-I at the ends of the three parts and joints of profile. It can be seen that the stresses of locations D and E at the ends of parts with thicknesses of 6 and 14 mm are relatively low, and the peak stresses during quenching are 33.5 and 27.7 MPa, respectively. The stress states of locations H and I at the joints of profile are compressive stress at the initial quenching stage, and then are gradually changed to tensile stress. The peak stress of location I (82.6 MPa) is larger than that of location H (59.2 MPa). However, for the locations F and G, the tensile stress first increases to a peak value, then decreases rapidly and translates into the compressive stress. After quenching for 5.5-6 s, the compressive stress reaches a peak value of about 100 MPa and keeps constant. Figure 17 shows the residual stress distribution of the extruded profiles after quenching. It is clear that there exists a large residual stress on the inner surface of joints of profile and the value is 60-95 MPa. This is mainly due to the fact that the cooling rate on the inner surface of the joints is much slower than that on the outer surface of joints, resulting in large compressive stress on the outer surface and large tensile stress in the centre and inner of joints. In the ends of part with the thickness of 10 mm, the residual stress is maximum with a value of 102 MPa due to the maximum cooling rate. However, the residual stress at the ends of parts with thicknesses of 6 and 14 mm is relatively low, and the stresses in most regions are lower than 30 MPa.
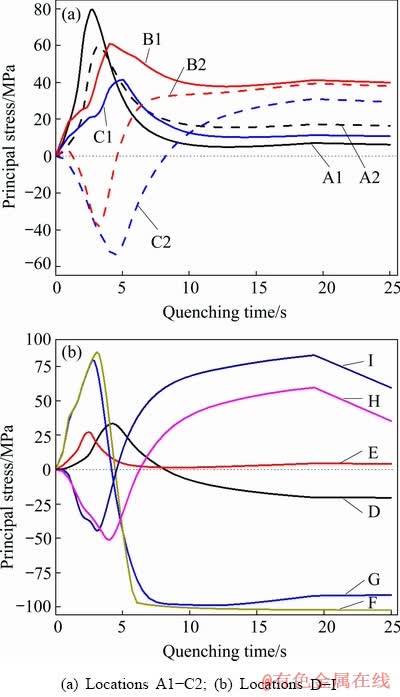
Fig. 16 Thermal stress evolutions at different locations during quenching

Fig. 17 Residual stress distribution of profile after quenching
4.3 Distortion during water quenching
During quenching, the thermal stress exceeds the yield strength of material at high temperatures, which may cause plastic deformation of profile. The distortion or profile surface cracks may occur once plastic deformation accumulates to some degree. Besides, the thermal and mechanical properties of material such as the elastic modulus, thermal expansion coefficient and yield strength, vary as quenching temperature changes, leading to a difference of deformation magnitude in each part of profile due to the non-uniform cooling. Figure 18 shows the residual deformation of extruded profiles after quenching for 25 s. It is clear that the profile presents a twisting-type distortion across the cross-section under non-uniform cooling. And severe outward bowing in the two parts with thicknesses of 6 and 14 mm is found. The maximum displacement of 9.51 mm is located at the end of part with the thickness of 6 mm. Figure 19 shows the variation of twisting angle during quenching. It can be seen that the twisting angle increases first to peak value and then decreases gradually, finally is maintained at 0.91°. As previously mentioned, cooling gradients would develop across the cross-section of profile during quenching, as shown in Fig. 12. During quenching, two stages occur in the history of the distortion due to the non-uniform cooling through the thickness of profile when cooling the profile from the outer surfaces [9]. In the first stage, the longitudinal contraction on the outer surfaces of three parts with different thicknesses is faster and larger relative to that on the inner surfaces and imposes an inward bowing of the cross-section. Then, as the outer surface cools, its cooling rate decreases while the cooling rate of the inner surface is still high because its temperature is high. The bowing direction varies and the part exhibits a outward bowing until the end of the quenching process. Consequently, the different type of bowing occurs in the different parts of profile, and the bowing rate is faster for the thin part than thick parts because it cools faster. Thus, the different bowing value and rate introduce twisting to the section. In addition, the distortion value in the part with thickness of 6 mm is obviously larger than that in the part with thickness of 14 mm. This is because the thickness of part plays a dual role in the outward bowing of the part. The temperature gradient through the thickness of part increases with the increasing thickness. Thus, larger distortions would be expected. However, as the thickness increases, the part becomes stiffer due to the increasing moment of inertia. At a large thickness, the role of the latter is more obvious. Consequently, the resultant of these two effects determines that the distortion of thin part is larger.
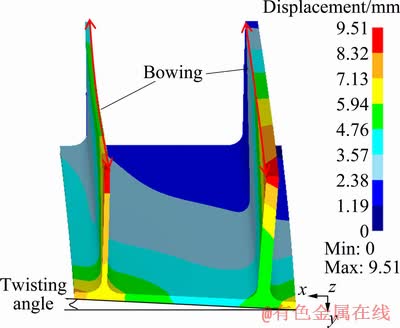
Fig. 18 Distortion type of profile during quenching

Fig. 19 Twisting history of profile during quenching
5 Conclusions
(1) Heat transfer coefficient first increases linearly with the decrease of interface temperature, then reaches peak value at the interface temperature of 108-180 °C due to both vigorous boiling and full fluid contact. After reaching the peak value, heat transfer coefficient decreases rapidly as interface temperature decreases. The heat transfer coefficient increases with increasing water flow rate. The peak heat transfer coefficient with the higher water flow rate appears at lower interface temperature.
(2) The simulated temperatures on the outer surface of profile during quenching are in good agreement with the measured ones and the maximum relative error is less than 12%, which indicates that the established thermo-mechanical coupling model is accurate and can be used to simulate the on-line quenching process of extruded profiles.
(3) The temperature distribution across the cross-section of profile during quenching is severe non-uniform and the maximum temperature difference is 300 °C at the quenching time of 3.49 s. The temperature difference through the thickness of different parts of profile first increases sharply to a maximum value, and then decreases gradually. The temperature gradient increases obviously with the increasing thickness of parts.
(4) The principal stress in the part with the thickness of 6 mm is tensile stress, while in the parts with the thicknesses of 10 and 14 mm is tensile-compressive stress. After quenching, there exist large residual stresses at the inner side of joints of profile and the two ends of part with thickness of 10 mm. The profile presents a twisting-type distortion across the cross-section under non-uniform cooling. The twisting angle increases firstly to the peak value of 2.78° and then decreases gradually, finally is maintained at 0.91°.
References
[1] YI J, WANG G, LI S K, LIU Z W, GONG Y L. Effect of post-weld heat treatment on microstructure and mechanical properties of welded joints of 6061-T6 aluminum alloy [J]. Transactions of Nonferrous Metals Society of China, 2019, 29(10): 2035-2046.
[2] XU W F, WU X K, MA J, LU H J, LUO Y X. Abnormal fracture of 7085 high strength aluminum alloy thick plate joint via friction stir welding [J]. Journal of Materials Research and Technology, 2019, 8(6): 6029-6040.
[3] WANG Y, ZHAO G, CHEN X, XU X, CHEN L, ZHANG C. Effect of inter-annealing between two stages of extrusion on the microstructure and mechanical property for spray deposited Al-Cu-Li alloy 2195 [J]. Journal of Materials Research and Technology, 2019, 8(5): 3891-3907.
[4] LIU Z, WANG G, YI J. Study on heat transfer behaviors between Al-Mg-Si alloy and die material at different contact conditions based on inverse heat conduction algorithm [J]. Journal of Materials Research and Technology, 2020, 9(2): 1810-1823.
[5] QI M, LI J, KANG Y. Correlation between segregation behavior and wall thickness in a rheological high pressure die-casting AC46000 aluminum alloy [J]. Journal of Materials Research and Technology, 2019, 8(4): 3565-3579.
[6] LIU Z W, LI L X, WANG G, YI J. Analysis and improvement of material flow during extrusion process using spreading pocket die for large-size, flat-wide, and multi-ribs profile [J]. The International Journal of Advanced Manufacturing Technology, 2020, 107(3-4): 1115-1129.
[7] LIU Z W, LI L X, LI S K, YI J, WANG G. Entrance shape design of spread extrusion die for large-scale aluminum panel [J]. The International Journal of Advanced Manufacturing Technology, 2019, 101(5-8): 1725-1740.
[8] BARBARA R, LORENZO D. Experimental, numerical, and analytical investigations on the charge weld evolution in extruded profiles [J]. The International Journal of Advanced Manufacturing Technology, 2018, 99(5-8): 1379-1387.
[9] YI J, WANG Z H, LIU Z W, ZHANG J M, HE X. FE analysis of extrusion defect and optimization of metal flow in porthole die for complex hollow aluminium profile [J]. Transactions of Nonferrous Metals Society of China, 2018, 28(10): 2094-2101.
[10] WANG D, ZHANG C, WANG C, ZHAO G, CHEN L, SUN W. Application and analysis of spread die and flat container in the extrusion of a large-size, hollow, and flat-wide aluminum alloy profile [J]. The International Journal of Advanced Manufacturing Technology, 2018, 94(9-12): 4247-4263.
[11] LI S K, LI L X, HE H, LIU Z W, ZHANG L. Influence of dynamic recrystallization on microstructure and mechanical properties of welding zone in Al-Mg-Si aluminum profile during porthole die extrusion [J]. Transactions of Nonferrous Metals Society of China, 2019, 29(9): 1803-1815.
[12] GOMES D F, TAVARES R P, BRAGA B M. Mathematical model for the temperature profiles of steel pipes quenched by water cooling rings [J]. Journal of Materials Research and Technology, 2019, 8(1): 1197-1202.
[13] LI M, LI Y D, BI G L, HUANG X F, CHEN T J, MA Y. Effects of melt treatment temperature and isothermal holding parameter on water-quenched microstructures of A356 aluminum alloy semisolid slurry [J]. Transactions of Nonferrous Metals Society of China, 2018, 28(3): 393-403.
[14] KANG L, ZHAO G, WANG G D, LIU K, TIAN N. Effect of different quenching processes following solid-solution treatment on properties and precipitation behaviors of 7050 alloy [J]. Transactions of Nonferrous Metals Society of China, 2018, 28(11): 2162-2172.
[15] KANG L, ZHAO G, TIAN N, ZHANG H T. Computation of synthetic surface heat transfer coefficient of 7B50 ultra-high- strength aluminum alloy during spray quenching [J]. Transactions of Nonferrous Metals Society of China, 2018, 28(5): 989-997.
[16] ZHANG J, DENG Y, YANG W, HU S, ZHANG X. Design of the multi-stage quenching process for 7050 aluminium alloy [J]. Materials Design, 2014, 56: 334–344.
[17] BIKASS S, ANDERSSON B, PILIPENKO A. Simulation of distortion due to non-uniform cooling in aluminium extrusion process [J]. International Journal of Material Forming, 2010, 3(1): 813–816.
[18] SHEPPARD T. Press quenching of aluminium alloys [J]. Materials Science and Technology, 1988, 4: 635-643.
[19] LOPEZ-GARCIA R D, GARCIA-PASTOR F A, MALDONADO-REYES A, JIMEMEZ-GOMEZ M A, RODRIGUEZ-GARCIA J A. Analysis of the effect of immersion rate on the distortion and residual stresses in quenched SAE 5160 steel using FEM [J]. Journal of Materials Research and Technology, 2019, 8(6): 5557-5571.
[20] YANG X, ZHU J, NONG Z, LAI Z, HE D. FEM simulation of quenching process in A357 aluminum alloy cylindrical bars and reduction of quench residual stress through cold stretching process [J]. Computational Materials Science, 2013, 69(1): 396-413.
[21] FU P, ZHOU P, XIE Z W, WU H Y, CHEN J G. Experimental and CFD investigations on cooling process of end-quench test [J]. Transactions of Nonferrous Metals Society of China, 2019, 29(11): 2440-2446.
[22] YANG X W, ZHU J C, LI W Y. CFD-supported optimization of flow distribution in quench tank for heat treatment of A357 alloy large complicated components [J]. Transactions of Nonferrous Metals Society of China, 2015, 25(10): 3399-3409.
[23] WANG M J, YANG G, HUANG C Q, CHEN B. Simulation of temperature and stress in 6061 aluminum alloy during online quenching process [J]. Transactions of Nonferrous Metals Society of China, 2014, 24(7): 2168-2173.
[24] YANG X W, ZHU J C, LAI Z H, LIU Y, HE D, NONG Z S. Finite element analysis of quenching temperature field, residual stress and distortion in A357 aluminum alloy large complicated thin-wall workpieces [J]. Transactions of Nonferrous Metals Society of China, 2013, 23(6): 1751-1760.
[25] NOWAK M, GOLOVKO O, NURNBERGER F, FROLOV I, SCHAPER M. Water-air spray cooling of extruded profiles: Process integrated heat treatment of the alloy EN AW-6082 [J]. Journal of materials engineering and performance, 2013, 22(9): 2580-2587.
[26] BIKASS S, ANDERSSON B, PILIPENKO A, LANGTANGEN H P. Simulation of the distortion mechanisms due to non-uniform cooling in the aluminum extrusion process [J]. International Journal of Thermal Sciences, 2012, 52(2): 50-58.
[27] BIKASS S, ANDERSSON B, PILIPENKO A, LANGTANGEN H P. Simulation of initial cooling rate effect on the extrudate distortion in the aluminum extrusion process [J]. Applied Thermal Engineering, 2012, 40: 326-336.
[28] EDELBAUER W, ZHANG D, KOPUN R, STAUDER B. Numerical and experimental investigation of the spray quenching process with an Euler-Eulerian multi-fluid model [J]. Applied Thermal Engineering, 2016, 100: 1259-1273.
[29] FENG X, ZHANG L, LI Z, LIU C. FEM simulation and experimental study on the quenching residual stress of aluminum alloy 2024 [J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2013, 227(7): 954-964.
[30] GOLOVKO O, FROLOV I, RODMAN D, NURNBERGER F, GRYDIN O, SCHAPER M. Spray cooling of extruded EN AW-6082 aluminium alloy sheets: spatial heat transfer coefficients [J]. Forschung im Ingenieurwesen, 2014, 78(3-4): 131–137.
[31] GUO R, WU J, FAN H, ZHAN X. The effects of spray characteristic on heat transfer during spray quenching of aluminum alloy 2024 [J]. Experimental Thermal and Fluid Science, 2016, 76: 211-220.
[32] FORESTIER R, MASSONI E, CHASTEL Y. Estimation of constitutive parameters using an inverse method coupled to a 3D finite element software [J]. Journal of Materials Processing Technology, 2002, 125: 594-601.
[33] STORCH R B, PIMENTEL L C G, ORLANDE H R B. Identification of atmospheric boundary layer parameters by inverse problem [J]. Atmospheric Environment, 2007, 41(7): 1417-1425.
刘志文1,2,易 杰2,李世康2,聂文杰1,李落星2,王 冠3
1. 南华大学 机械工程学院,衡阳 421001;
2. 湖南大学 汽车车身先进设计制造国家重点实验室,长沙 410082;
3. 宁夏大学 机械工程学院,银川 750021
摘 要:采用反向热传导算法并结合一维末端水淬试验求解热型材与冷却水的界面换热系数。以确定的换热系数作为热边界条件,基于Deform-3D仿真平台建立不等厚壁挤压铝型材在线水淬过程的三维热力耦合模型。系统研究型材水淬过程中的温度场、残余应力场和截面畸变。研究结果表明:随着冷却水流量的增加,界面换热系数增大;高冷却水流量的峰值换热系数出现在低的界面温度;型材淬火过程中横截面上的温度分布严重不均匀,淬火时间为3.49 s时最大温差为300 °C;通过型材横截面不同壁厚部位的温差先急剧增大到峰值,然后逐渐减小;随型材各部位壁厚的增加,温度梯度明显增大;淬火完成后在型材接头内侧和壁厚为10 mm部位的两端存在较大的残余应力;非均匀冷却条件下,型材淬火过程中横截面呈现扭曲型畸变,最大扭曲角为2.78°。
关键词:铝型材;不等厚壁;水淬;换热系数;热力耦合模型
(Edited by Xiang-qun LI)
Foundation item: Project (51605234) supported by the National Natural Science Foundation of China; Projects (2019JJ50510, 2019JJ70077) supported by the Natural Science Foundation of Hunan Province, China; Projects (18B285, 18B552) supported by Scientific Research Fund of Hunan Provincial Education Department, China
Corresponding author: Jie YI, Tel: +86-15111270111, E-mail: 15111270111@163.com;Guan WANG, Tel: +86-13895189949, E-mail: belonging@163.com
DOI: 10.1016/S1003-6326(20)65290-6

