Theoretical analysis and simulation of measuring method on alternating micro capacitor
KONG Quan-cun(孔全存)1, 2, LIU Gui-li(刘桂礼)1, ZHUANG Hai-han(庄海涵)3
(1.School of Opto-Electronics Information & Communication Engineering, Beijing Information Science & Technology University, Beijing 100192, China;
2. Department of Precision Instrument&Mechanology, Tsinghua University, Beijing 100084, China;
3. School of Instrument Science & Opto-Electronics Engineering, Beihang University, Beijing 100191, China)
Abstract: A theoretical model for alternating micro capacitor measurement based on the biased voltage was established, and a quivalent circuit model on the basis of first-order approximate solution was put forward. The theoretical model was solved by classical series analytical method and numerical method based on the single step Runge-Kutta, respectively. Theoretical analysis and numerical calculations show that the relative error between theoretical approximate value and numerical simulation results is less than 0.02% except for very few points where the error is about 0.2%, when the ratio of dynamic and static capacitance is less than 0.01. The results also prove the correctness of detection models and provide a theoretical reference for the circuit design of AMC.
Key words: alternating micro capacitor measurement; biased voltage; theoretical model; numerical solution
CLC number: TH701 Document code: A Article ID: 1672-7207(2011)S1-1062-06
Micro capacitor measuring techniques are widely adopted in many fields as sensors. Alternating micro capacitor (AMC) is the pick-up component of micro- resonator, which is the basic mechanical unit in the microstructure of micro-electro-mechanical system (MEMS) devices. The performance of micro-resonator is directly affected by the measuring accuracy of AMC. The measuring method for AMC based on biased voltage (BV) has features such as simple circuit structure, easy implement, high reliability, fast response and little signal distortion. As a non-contact measureing method, AMC measurement has been widely used for the measurement of resonator[1-2]. With the rapid development of MEMS technology, micro-comb capacitor is widely used as the pick-up and detection device of resonators[3]. For example, AD Corp. employs the differential capacitor way to measure the displacemt or vibration amplitude of mass in ADX series gyro and accelerometers[4]. The resonator gyro designed by Draper Lab has two sets of detection electrodes. One set of detection electrodes is used as the primary vibration pick-up of mass and the other set is employed to detect the negative vibration of mass that caused by Coriolis effect. For both applications, the so-called differential switched-capacitor test method[5] is adopted in the AMC measurement. The differential switched-capacitor test method is particularly suitable to detect AMC in the order of magnitude of kHz. For higher frequency vibration of a resonance, this method is inapplicable because of its too much time expenditure during demodulation and integration. The biased voltage (BV) measuring method is still widely used in vibration measurement of the order of magnitude of 100 kHz or more, and it is especially suitable for measuring the static capacitor with magnitude of 1~10 pF attached by alternating capacitor with magnitude in fF order. This method has many advantages such as simple structure, high reliability and good compatible with the process that fabricated resonators using complementary metal oxide semiconductor (CMOS) technology, easy integration, and etc. This detective method is applied during the research and development of all types of MEMS resonators[6-8]. When this method is adopted, the signal frequency response of resonators is good and the output signal magnitude can reach 100 mV. Moreover, the higher the frequency, the smaller the distortion.
In this study, according to the basic principle of the AMC measurement based on BV, a mathematical model was proposed considering the impact of detection circuit. According to the mathematical model, the AMC measuring method based on BV was proved suitable for the measuring of time-varying circuits. Furthermore, the equivalent circuit model of the measuring method was established.
1 Mathematical model of AMC measurement
based on BV
The working process of AMC measurement based on BV can be described as follows: firstly, a biased direct current (DC) voltage is applied to the capacitor by external circuits so that certain charges are accumulated across the capacitor; the voltage across the capacitor would change when the capacitance changes instantaneously and the amount of the voltage change represents the change in capacitor. However, the change of electric charge caused by capacitance change would lead to an alternating voltage in actual measuring circuits. Capacitor value itself would couple with this alternating voltage by the interaction between alternating voltage and capacitance. In addition, the high-pass filter circuit, which consists of the input impedance of measuring circuit and capacitor together, would also cause distortion of the signal.
Conventional circuit model analysis, e.g. the time-domain analysis mothed, frequency domain analysis and Laplace transform method, are all linear circuit models based on ordinary differential equations (ODE) and the capacitance is treated as a constant. These conventional methods are not suitable to analyze the time-varying capacitor in measuring circuits. In this study, a nonlinear mathematical model of the AMC measurement is put forward, in which many factors (input BV, AMC and input resistance of measuring circuit) are synthetically considered. The circuit model of AMC measurement is shown in Fig.1, and the loop voltage Eqs. (1) and (2) could be be listed according to Kirhhoff’s voltage law. Equivalent circuit model of AMC measurement based on BV is shown in Fig.2.
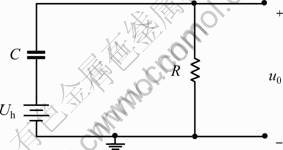
Fig.1 Circuit model of AMC measurement based on BV
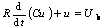 (1)
(1)
u0 = Ub – u (2)
where C is the capacitance to be detected, u is the voltage across the capacitor, R is the input impedance, Ub is the DC BV of the circuit and u0 is the actual output voltage in measuring circuit.
When C changes with time, Eq. (1) is no longer ODE. Traditional analysis methods, such as Fourier analysis (frequency domain analysis) and Laplace transform method would no longer fit. This work adopts trigonometric series solution to solve Eq. (1). Meanwhile, under this condition, C is a typical sinusoidal variation superimposed constant term, and Eq. (1) is solved. The variation of capacitor C is assumed as:
C = C0 + C1cosω0t (3)
where C0 is the constant part of the test capacitance (static capacitance), C1 is the amplitude of the alternating capacitor to be detected, ω0 is the frequency of the variation of alternating capacitor. Under this situation, the steady-state voltage across the capacitor has periodic function with the change of frequency ω0 as:
u(t) = u(t+ nT0) (n = 1, 2, …) (4)
where T0=2π/ω0 is the changing cycle of capacitance. So u(t) could be expanded in Fourier series form as:
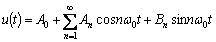 (5)
(5)
Further calculations can be expressed as:
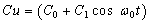
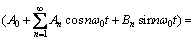
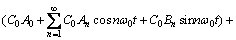
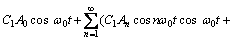
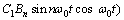 (6)
(6)
The first derivative of time to Eq. (6) is calculated, the result and Eq. (5) are substituted into Eq. (1), and the equation about the coefficient sequence could be obtained as (double frequency item and above are omitted):

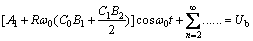 (7)
(7)
In Eq. (7), as sinnωt and cosnωt are mutually orthogonal, each corresponding coefficient of the left and right ends of the equation equals to zero:
 (8)
(8)
Actually, the magnitude of C1 is often 3 orders lower or more than that of C0, that is C1<0. So the first order approximation solution of Eq. (1) by using the Eq.(8) is solved. Set An = 0, Bn = 0 (n > 1), the baseband linear equations can be obtained, and the solution of Eq. (8) is:
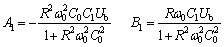 (9)
(9)
Thus, the voltage signal u(t) across the capacitor could be expressed. According to Eq. (2), the effective output signal u0 of AMC measuring circuit based on BV is expressed as:
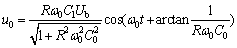 (10)
(10)
Eq. (10) is just a mathematical expression of a first order high-pass filter circuit[9]. According to the relationship between magnitude and phase, it could be determined that the high-pass filter circuit exhibited in Fig.2 is the equivalent one shown in Fig.1. In the circuit of Fig.2, when C0 = C and Rin = R, the circuit input signal is:
uin = ( UbC1/C0 )cosωt (11)
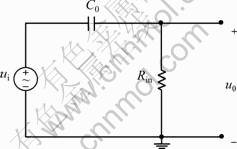
Fig.2 Equivalent circuit model of AMC measurement based on BV
Eq.(11) demonstrates that the equivalent input signal source caused by the alternating capacitance is proportional to the biased voltage as well as C1/C0, which has nothing to do with the absolute value of capacitance (static capacitance and alternating capacitance). Fig.2 shows that C0 and Rin (the input impedance of the rear measuring circuit) are composed of the first order high-pass network. If this method is adopted to design the AMC measuring circuit, this input impedance should be selected and the frequency of AMC measuring circuit should also be chosen in the passband of the high-pass filter.
From the equivalent model, it can be seen that the AMC measurement based on BV has very good high frequency response characteristics compared with other measuring methods of capacitor. It is especially suitable for the applications of covering high resonance frequency. Besides, the measuring circuits are very simple, they can directly output the signal that is proportional to the capacitor variation.
2 Simulation of equation numerical solution
When a set of parameters is given, Eq. (1) could be solved by using single-step Runge-Kutta method of fourth order. According to the equivalent circuit shown in Fig.2, the model can be divided into two parts. One is the equivalent power and the other is a high-pass filter composed of the capacitor and resistance. So the equivalent circuit of two parts can be compared respectively.
The amplitude-frequency and phase-frequency characteristics of equivalent transfer function are compared without considering the impact of the input amplitude.
When the three parameters (Ub, C0 and C1) are changed within the pass-band frequency, whether the equivalent signal source is on equal amplitude with Eq. (11) is unvestigated.
This work uses Ode45 function in Matlab to simulate the model. If the residual precision is set to 10-8 order of magnitude, the iterative error between the numerical solution and exact one can be guaranteed in 10-8 order.
2.1 Comparison of transfer function
The transfer function H(s) for the RC network consisted of high-pass filter circuit shown in Fig.2 is H(s)=RCs/(RCs+1). Amplitude-frequency and phase- frequency characteristics of the function are expressed as:

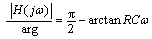 (12)
(12)
Eq. (12) is drawn as logarithmic curve by the continuous solid dotted line in Fig.3. The numerical solutions of Eq. (1) are shown in Fig.4 (The output signal amplitude is calculated using the output signal after 4 μs to eliminate the transient conditions caused by the initial conditions). According to Eq. (11), the amplitude is divided by the constant of UbC1/C0, and the equivalent transfer gain of sign could be extracted. After the operating frequency is set as horizontal coordinate and the transmission gain multiplied by 20 times logarithmic was set as vertical coordinate, the amplitude-frequency characteristics chart is marked with hollow triangles in Fig.3. The sweep frequency simulation is done from 100 Hz to 10 MHz. The theoretical values, simulation values and the relativeerror in every point of sweep frequency are listed in Table 1.
Table 1 Error comparision of theoretical approximate value with numerical simulation results of transfer function
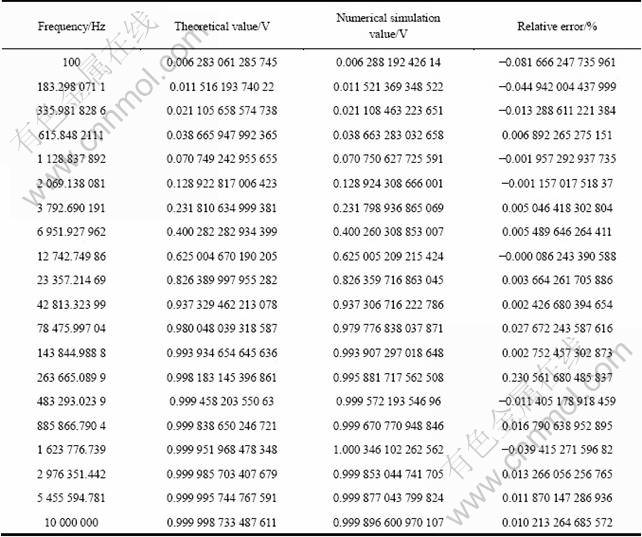
Table 1 demonstrates that the relative error between theoretical approximate value and numerical simulation results is below 0.02% except for very few points where the error is about 0.2%, when the sweeping frequnency ranges from 100 Hz to10 MHz.
When the operating frequency is set as horizontal coordinate and the phase difference between numerical simulation signal shown in Fig.4 and cosω?t is set as vertical coordinate, the phase frequency plane is shown in Fig.3. Fig.3 demonstates that the theory analysis results of the transfer function are in good agreement with the numerical simulation ones.
The comparision between the approximation theoretical model and numerical analysis results shows that the approximation theoretical model is correct. Therefore, in an actual circuit design process, when the AMC is far below the steady-state capacitance, the measuring equivalent circuit can be designed according to Fig. 2.
2.2 Comparison of equivalent signal source model
The operating frequency of numerical simulation calculation is set in the high-pass filter passband, which is made up of the equivalent RC network. When ω0>>1/(RC), the gain of RC network equals to 1 and the phase difference between input and output equals to 0. Then, the output signal u0 represents the quivalent power uin. By changing Ub, C0 and C1, comparing output amplitude of Eq. (11) with UbC1/C0, the signal source model is verified.

Fig.3 Caparison with transfer function
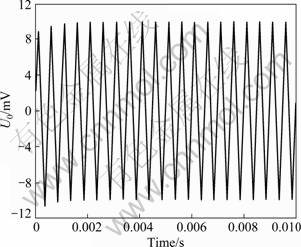
Fig.4 Numerical calculation results of Eq.(1)
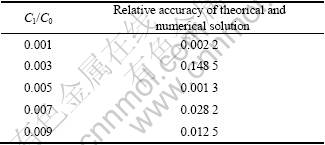
In Fig.5, continuous soild line represents Ampli= C1Ub/C0, where Ampli is the amplitude of the theorical equivalent input signal, C1/C0 is set according to actual circuit, Ub is horizontal coordinate. The hollow triangles denote the amplitude of output signal obtained by numerical simulation, when ω0>>1/(RC). The lines in the graph represent different values of C1/C0, and the values are 0.001, 0.003, 0.005, 0.007 and 0.009 respectively from bottom to top.
From Fig.5, it can be seen that the equivalent input
signal strength of theorical approximate model can be represented by the approximate formula Ampli=C1Ub/C0. Table 2 shows the relative error caused by the two methods in five curves.
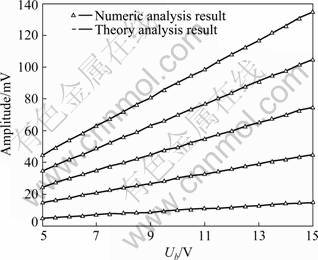
Fig.5 Comparision of solution between theory and numerical simulation of equivalent input signal amplitude
Table 2 Relative error of two methods in Fig.5
3 Conclusions
(1) The equivalent circuit model is a good approximation with the actual situation that the high-order error in most cases is less than 0.02%, when the ratio of dynamic and static capacitance is equal or less than 0.01(i.e.C1/C0 ≤ 0.01). Since the correctness of the theoretical model is proved, the model provides a design method for the application of AMC measurement based on BV.
(2) From the equivalent circuit, the alternating part of capacitor does not affect the passband of the equivalent high-pass filter, and the cut-off frequency is only related with the static capacitance C0. The input impedance of measuring circuit is determined according to the operating frequency and the static capacitance in measuring circuit, so it can be guaranteed that the operating frequency is within the pass band of the equivalent circuit.
(3) From the equivalent signal source, it is shown that the ampitude of the measuring signal is proportional to the DC biased voltage Ub and the ratio of the dynamic and static capacitance (i.e. C1/C0), which provides a reference for the design of mechanical structure and the selection of DC biased voltage.
Acknowledgments
The authors would thank Modern Electronic Technology Lab of School of Opto-Electronics Information&Communication Engineering of Beijing Information Science & Technology Univeristy for their designing and computing resources and post Ph.D LI Jian-li for many helpful discussion.
References
[1] Tan Xiao-yun, Xiong Jun, Study of a facile signal demodulation pre-circuit for differential capacitance detection[J]. Chinese Journal of Scientific Instrument, 2005, 6(suppl): 6.
[2] Zhu Wu, Zhang Jia-min, Xiong Bin, Research of Detecting Technique of Micro Differential Capacitance[J]. Journal of Test and Measurement Technology, 2004, 18(3): 203-207.
[3] Eloy J C. Status of the MEMS industry in 2006[J]. Sensors and Transducers, 2006, 66(4): 521-525.
[4] Product Datasheets; Analog Devices, Norwood, MA. http://www. analog. com.
[5] Tanga W C, Nguyen T C H, Judy M W, et al. Electrostatic comb drive of laterally driven resonators[C]// Proceeding of Transducers’89, Montreaux, Switzerland, 1989: 25-30.
[6] Nguyen C T C, Howe R T. CMOS micromechanical resonator oscillator technical digest[C]// 1993 International Electron Devices Meeting. Washinton D C. 1993: 199-202.
[7] Roessig T A, Howe R T, Pisano A P. Nonlinear Mixing in Surface-Micromachined Tuning Fork Oscillators[C]// 1997 IEEE International Frequency Control Symposium. Orlando, US. 1997: 778-782.
[8] Nguyen C T C, Howe R T. Design and Performance of CMOS Micromechanical Resonator Oscillators[C]// 1994 IEEE International Frequency Controal Symposium. Boston, US. 1994: 127-134.
[9] Hua Cheng-ying, Tong Shi-bai. Analog Electronics[M]. Beijing: Higher Education Press, 2006: 240-256.
(Edited by FANG Jing-hua)
Foundation date: Project (1025004) supported by the Foundation of Beijing Information Science & Technology Univeristy, China
Received date: 2011-04-15; Accepted date: 2011-06-15
Corresponding author: KONG Quan-cun, lecturer, PhD candidate; Tel: 010-82426919; E-mail: kongquancun@163.com