DOI: 10.11817/j.issn.1672-7207.2019.03.021
基于井筒-射孔模型的地层破裂压力及起裂角的理论研究
范勇1, 2,赵彦琳1, 2,朱哲明1, 2,周昌林1, 2,张宪尚1, 2
(1. 四川大学 深地科学与工程教育部重点实验室,四川 成都,610065;
2. 四川大学 建筑与环境学院,四川 成都,610065)
摘要:为了研究不同参数对水力压裂中地层破裂压力和水力裂缝起裂角的影响规律,利用井筒-射孔模型,将射孔简化为裂缝,采用保角映射的方法求得射孔端部的应力强度因子;根据最大拉应力准则求得射孔端部水力裂缝的起裂角和地层破裂压力的理论公式。为了验证该方法的有效性,将理论值与文献中的实验结果和工程实际值进行对比。研究结果表明:理论值与实验结果和工程实际值均吻合较好。水力裂缝的起裂角随主应力差、射孔长度和射孔角度的增大而增大;最优射孔方位角应在0°~15°范围内;最优射孔长度应为井筒直径的2~3倍。
关键词:水力压裂;射孔;应力强度因子;地层破裂压力;起裂角
中图分类号:TU45 文献标志码:A 文章编号:1672-7207(2019)03-0669-10
Theoretical study of break down pressures and fracture initiation angles based on model containing wellbore and perforations
FAN Yong1, 2, ZHAO Yanlin1, 2, ZHU Zheming1, 2, ZHOU Changlin1, 2, ZHANG Xianshang1, 2
(1. MOE Key Laboratory Deep Underground Science and Engineering, Sichuan University, Chengdu 610065, China;
2. College of Architecture and Environment, Sichuan University, Chengdu 610065, China)
Abstract: In order to study the influences of perforation parameters on break down pressures and hydraulic crack initiation angles, a 2D model containing perforations and wellbore was established to simplify the perforations as a crack. By conformal mapping techniques, the stress intensity factors at perforation tips were obtained. The theoretical method to calculate break down pressure and initiation angle was acquired according to the maximum tensile failure criterion. For validating the theoretical solutions, the experimental results and the in-situ test results were compared with the calculated results. The results show that they are in good agreement. The hydraulic crack initiation angles increase with the increase of two principal stresses, the perforation lengths and the perforation azimuths. The optimal perforation azimuth is between 0° to 15° with the major principal stress. The optimal perforation length is between 2 and 3 times wellbore diameter.
Key words: hydraulic fracturing; perforation; stress intensity factor; break down pressure; initiation angle
水力压裂中,射孔是油气完井工程的重要组成部分,一方面,射孔连通复杂储层与井眼,能提高射孔完井的作业效率和油气产量;另一方面,能合理保护储集层,延长油气藏的开发寿命[1]。但是,由于钻井过程的不确定性以及地层的复杂性,有效预测射孔破裂压力和水力裂缝的延伸方向是水力压裂增产过程中所面临的重要挑战[2]。随着射孔完井技术的广泛应用,国内外学者对射孔井地层破裂压力和水力裂缝扩展问题进行了大量的研究。试验研究方面,HALLAM等[3]选取长×宽×高为304.8 mm×304.8 mm×304.8 mm的立方体岩心模拟地层,模型中央钻取直径为6.35 mm的圆柱形井眼,分别对裸眼及套管井模型进行水力压裂试验并观察压裂后水力裂缝的连通情况,研究表明:裸眼井情况下水力裂缝的起裂方位具有随机性,而套管井中水力裂缝总是在射孔段起裂,裂缝延伸平面垂直于最小地应力方向。与射孔连通的水力裂缝的长度与射孔方位角有关,方位角越小,水力裂缝越长。BEHRMANN等[4]选用大型砂岩立方体试件研究套管井中不同射孔参数对水力裂缝起裂的影响,结果表明裂缝起裂方位与射孔方位、压裂液特性以及注入排量有关。VAN 等[5]试验研究了射孔相位、间距、射孔轴线相对于最优起裂面的角度等参数对水力裂缝的影响,研究结果表明:90°相位角最不利于相邻射孔间裂缝的连通,射孔最好沿0°或180°相位成直线排列。JIN等[6-7]采用含射孔的水泥砂浆模型进行水力压裂试验,研究不同射孔参数对起裂压力和起裂角的影响。数值模拟方面,门晓溪等[8]采用RFPA软件研究了不同射孔角度对水力裂缝扩展的影响,研究结果表明:无论射孔角度如何变化,裂纹的扩展方向始终趋向于最大主应力方向;随着射孔角度的增加,逐渐形成双翼型转向裂纹,且射孔方位角越大,裂纹的转向越明显,转向距离越大;最佳射孔方位角范围为0°~30°。彪仿俊等[9]基于有限分析软件研究了螺旋射孔条件下,不同射孔参数(如射孔方位角、相位角和射孔密度)对地层破裂压力的影响,并给出了地层破裂压力的变化规律。王素玲等[10]利用有限元分析方法研究了低渗透储层中不同射孔参数对地层破裂压力的影响,并根据计算结果给出了最优射孔参数。张广清等[11]采用有限元法系统分析了垂直井中射孔对地层破裂压力的影响,结果表明:射孔密度和射孔方位角是影响地层破裂压力的主要因素,射孔孔眼长度和射孔孔眼直径对其影响不大。尽管在试验和数值模拟方面对射孔参数(如射孔密度,射孔直径,射孔长度和射孔方位角等)进行了丰富的研究和讨论,但射孔参数对水力裂缝的影响规律更应该深入的理论研究。理论研究方面,YEW等[12]运用三维弹性理论建立了裸眼斜井的起裂压力计算模型,认为剪应力分量会影响起裂压力以及水力裂缝的起裂方位;HOSSAIN等[13]推导了垂直井和水平井中裸眼完井和射孔完井等6 种情况下地层起裂时所需的破裂压力, 并得出裂缝起裂方向和孔眼轴线间的夹角,但他们均将井筒或射孔简化为二维情况下无限大板中受压圆孔的问题,并得到圆孔周边的应力状态,根据最大拉应力准则求得地层破裂压力;因而忽略了井筒和射孔之间的相互作用和影响。唐世斌等[14-15]将射孔视为成裂缝,并将射孔与井筒的模型简化为二维情况下圆孔周边含对称双裂缝的问题,分别采用应力强度因子手册中经验公式和权函数的半解析法求解裂缝尖端的应力强度因子,并且基于最大拉应力准则得到地层破裂压力和起裂角的解析解。在此,本文作者主要研究180°相位的对称双射孔模型,基于井筒-射孔模型,同时考虑两者的相互影响,并基于弹性力学中的保角变换方法[16]推导地层破裂压力和水力裂缝起裂角的理论计算方法。
1 破裂压力和裂缝起裂角的理论分析
1.1 井筒-射孔模型
在实际工程中,射孔的长度和井筒的直径均远大于射孔的直径,比如大庆敖332-32井[10]中射孔直径为10 mm,射孔长度为500 mm(为射孔直径的50倍),井筒直径为178 mm(为射孔直径的17.8倍)。因此,同时研究射孔和井筒时,相对于其他因素,可以不计射孔直径的影响。将含射孔和井筒的模型简化为无限大平面中圆孔双裂缝的模型,如图1所示。
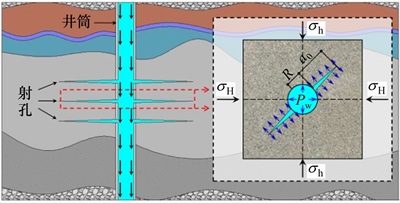
图1 射孔-井筒模型的计算简图
Fig. 1 Model containing wellbore and perforations
本文假设:
1) 储层岩石为各向同性材料;
2) 储层岩石处于线弹性状态下的均匀介质,忽略孔隙的影响;
3) 不考虑岩石与压裂液物理化学作用而引起力学性质的变化;
4) 孔眼轴线与井壁垂直相交,井筒和孔眼间连通性良好,作用在井壁和射孔内的流体压力相等。
1.2 射孔尖端的应力强度因子
对于圆孔双裂缝问题,TADA等[15]采用边界配点法得到圆孔双裂缝Ⅰ和Ⅲ型应力强度因子的半解析公式,但并未提出Ⅱ型裂缝的应力强度因子。因而,本文采用复变函数方法[16-19]求解射孔尖端Ⅰ和Ⅱ型的应力强度因子的解析公式。
采用保角变换的方法将z平面上井筒和射孔以外的岩石区域,映射到ξ平面上中心单位圆的内部,z平面上井筒和射孔的边界即被映射到单位圆的圆周上。郭俊宏等[20]提出了该问题的映射函数:
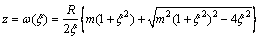 (1)
(1)
式中: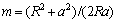 ;
;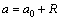 ,a0和R分别为射孔长度和井筒的半径。在z平面上,
,a0和R分别为射孔长度和井筒的半径。在z平面上,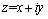 ;在ξ平面上,
;在ξ平面上, ,
,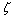 和
和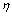 分别为
分别为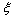 平面上的横坐标和纵坐标。
平面上的横坐标和纵坐标。
采用式(1)的映射函数,可将z平面上射孔和井筒外部的储层岩石区域映射到ξ平面中单位圆的内部(含圆周边界),如图2所示。z平面中射孔和井筒边界上的关键点,可由表1所示的关系映射到ξ平面中单位圆圆周上的关键点。因此,采用如式(1)所示的保角变换关系,射孔和井筒的问题可以转化为研究单位圆的问题。
由式(1)计算可得
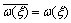 (2)
(2)
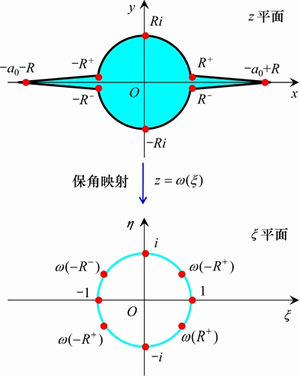
图2 保角映射示意图
Fig. 2 Sketch of conformal mapping method
表1 关键点的映射关系
Table 1 Mapping relations of key points
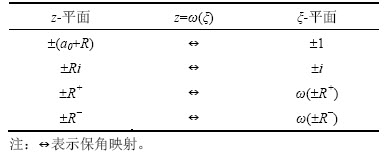
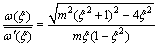 (3)
(3)
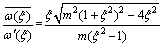 (4)
(4)
由图1可知:射孔和井筒主要承受模型边界上的水平地应力(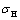 和
和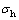 分别为最大、最小水平地应力,如图3(b)所示)与内部压裂液产生的压力Pw,如图3(c)所示。因此本文可将原模型分解为这2部分应力的叠加,如图3所示。
分别为最大、最小水平地应力,如图3(b)所示)与内部压裂液产生的压力Pw,如图3(c)所示。因此本文可将原模型分解为这2部分应力的叠加,如图3所示。
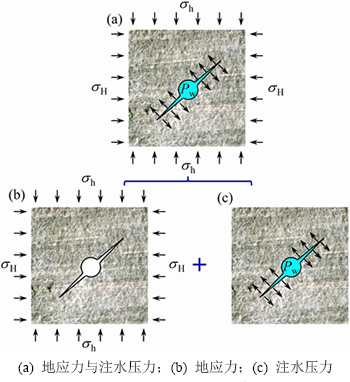
图3 应力的叠加原理示意图
Fig. 3 Sketch of superposition principle
针对图3(b)所示情况,射孔完井仅仅承受最大最小水平地应力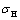 和
和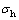 作用时,在ξ平面的单位圆边界上,ξ=σ,则函数
作用时,在ξ平面的单位圆边界上,ξ=σ,则函数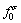 可以表示为
可以表示为
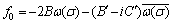 (5)
(5)
式中: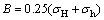 ;
;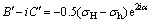 ;
; 为射孔轴线与最大水平地应力
为射孔轴线与最大水平地应力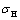 之间的夹角(记作射孔方位角)。将式(2)代入式(5),式(5)可简化为
之间的夹角(记作射孔方位角)。将式(2)代入式(5),式(5)可简化为
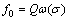 (6)
(6)
式中: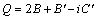 。
。
根据复变函数基本原理[16],地应力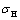 和
和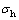 作用下的应力函数
作用下的应力函数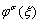 可以表示为
可以表示为
 (7)
(7)
式中: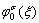 可由下式求得
可由下式求得
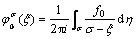 (8)
(8)
根据Cauchy积分方法和解析延拓公式,将式(5)代入式(8)可得
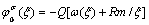 (9)
(9)
最后将式(9)代入式(7),地应力作用下的应力函数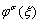 为
为
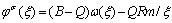 (10)
(10)
同理,针对图3(c)所示情况,当射孔完井仅仅承受射孔和井筒内压裂液压力Pw时,在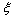 平面的单位圆边界上,函数
平面的单位圆边界上,函数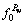 可以表示为
可以表示为
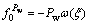 (11)
(11)
因此,在注水压力Pw作用下的应力函数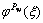 可以表示为
可以表示为
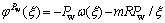 (12)
(12)
由应力的叠加原理可得,压裂液压力Pw以及地应力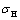 和
和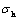 共同作用下的应力函数
共同作用下的应力函数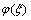 可由2部分叠加而得:
可由2部分叠加而得:
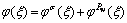 (13)
(13)
根据文献[16],射孔尖端的应力强度因子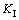 和
和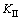 由下式可得
由下式可得

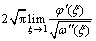 (14)
(14)
将式(13)和式(1)代入式(14)可得,压裂液压力和地应力共同作用下射孔端部的应力强度因子分别为
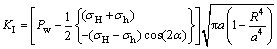 (15)
(15)
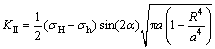 (16)
(16)
1.3 水力裂缝的起裂角
断裂力学中射孔尖端的周向应力σθθ为
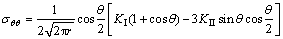 (17)
(17)
式中:r和θ分别为射孔尖端的极坐标,如图4所示。
当射孔端部的最大周向应力σθθ大于储层岩石的抗拉强度σt时,射孔开始起裂,此时水力裂缝扩展的方向与射孔轴线的夹角为起裂角θ0,即
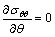 ,
,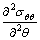 <0 (18)
<0 (18)
将式(17)代入式(18)可得
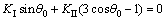 (19)
(19)
当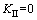 时,起裂角
时,起裂角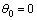 ;当
;当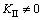 时,令
时,令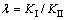 ,起裂角
,起裂角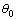 为
为
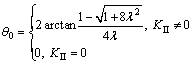 (20)
(20)
式中: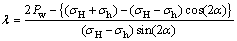 。
。
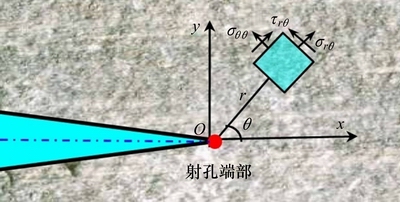
图4 射孔尖端的极坐标
Fig. 4 Polar coordinates at perforation tip
1.4 地层破裂压力
当射孔开始起裂时,水力裂缝的起裂角为θ0,即式(20),此时射孔和井筒内压裂液压力即为地层破裂压力。将式(20)代入式(17)可得:
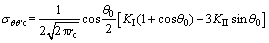 (21)
(21)
式中: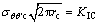 ,
, 为围压作用下储层岩石的Ⅰ型断裂韧度。因此,将应力强度因子KI和KII,即式(15)和式(16),代入式(21)可得地层破裂压力Pb为
为围压作用下储层岩石的Ⅰ型断裂韧度。因此,将应力强度因子KI和KII,即式(15)和式(16),代入式(21)可得地层破裂压力Pb为

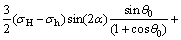
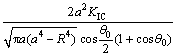 (22)
(22)
式中:地层破裂压力Pb是一个隐式的表达式,该问题宜采用迭代方法进行求解。首先,根据不同的工况,输入射孔参数(射孔长度a0和方位角 ,井筒半径R)和地层应力(
,井筒半径R)和地层应力( 和
和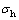 )并将井筒和射孔内压裂液的压力Pw置为0,其次,由式(15)和(16)可分别得到射孔尖端的Ⅰ型和Ⅱ型应力强度因子KI和KII,并由式(20)计算水力裂缝的起裂角θ0;根据式(22)可得地层破裂压力Pb。若该地层破裂压力Pb不满足Pw=Pb,则缓慢增加Pw并重新计算;若该地层破裂压力Pb满足Pw=Pb,则输出水力裂缝的起裂角θ0和地层破裂压力Pb,求解过程如图5所示。
)并将井筒和射孔内压裂液的压力Pw置为0,其次,由式(15)和(16)可分别得到射孔尖端的Ⅰ型和Ⅱ型应力强度因子KI和KII,并由式(20)计算水力裂缝的起裂角θ0;根据式(22)可得地层破裂压力Pb。若该地层破裂压力Pb不满足Pw=Pb,则缓慢增加Pw并重新计算;若该地层破裂压力Pb满足Pw=Pb,则输出水力裂缝的起裂角θ0和地层破裂压力Pb,求解过程如图5所示。

图5 求解破裂压力和裂缝起裂角的流程图
Fig. 5 Flow chart for calculating break down pressure Pb and initiation angles θ0 of hydraulic cracks
由式(22)可知,地层破裂压力Pb主要由以下3部分组成:
1) 垂直于射孔轴线地应力分量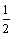
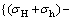
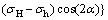 ;
;
2) 沿射孔轴线的地应力分量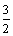
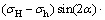
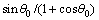 ;
;
3) 储层岩石的抗拉强度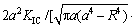
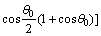 。
。
2 破裂压力和裂缝起裂角的验证
2.1 试验值与理论值的对比
JIN等[6-7]采用水泥砂浆试件进行水力压裂试验,其试样长×宽×高为300 mm×300 mm×300 mm,井筒直径D为15 mm,射孔长度a0为30 mm。射孔方位角 分别取0°,15°,30°,45°和60°;最大水平地应力
分别取0°,15°,30°,45°和60°;最大水平地应力 分别为4和6 MPa;最小水平地应力
分别为4和6 MPa;最小水平地应力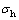 为1 MPa。为了分析不同地应力的影响,本文采用RENSHAW等[21]的建议定义水平应力差为
为1 MPa。为了分析不同地应力的影响,本文采用RENSHAW等[21]的建议定义水平应力差为
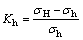 (23)
(23)
试验中Kh分别取3和5,JIN[6]建议断裂韧度KIC分别取值为2.3 MPa·m1/2和2.9 MPa·m1/2。水力压裂试验过程中,文献[6-7]中,射孔端部破裂时井筒内的破裂压力Pb如图6所示。射孔端部水力裂缝的起裂角θ0[6]如图7所示。此外,将射孔参数和地层应力代入本文的计算理论方法,求得地层破裂压力Pb和水力裂缝起裂角θ0的理论值。
由图6可知:井筒和射孔内的破裂压力Pb的试验值与理论值基本吻合。当射孔方位角 为0°和60°时,试验值与理论值之间存在一定的偏差。这主要是因为:1) 理论模型基于无限大平面,而试验模型是有限尺寸;2) 试验中水泥砂浆模型具有不均匀性,试验值存在一定的离散性。但当射孔方位角
为0°和60°时,试验值与理论值之间存在一定的偏差。这主要是因为:1) 理论模型基于无限大平面,而试验模型是有限尺寸;2) 试验中水泥砂浆模型具有不均匀性,试验值存在一定的离散性。但当射孔方位角 为15°,30°和45°时,两者相差不大。此外,当水平应力差系数Kh=3时,试验值基本与理论预测值重合。因此,在总体趋势上地层破裂压力Pb的理论值基本符合模型试验值。
为15°,30°和45°时,两者相差不大。此外,当水平应力差系数Kh=3时,试验值基本与理论预测值重合。因此,在总体趋势上地层破裂压力Pb的理论值基本符合模型试验值。
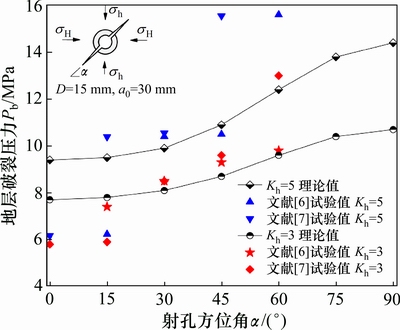
图6 破裂压力Pb的试验值与理论值的对比图
Fig. 6 Comparison of break down pressure Pb between theoretical and experimental results
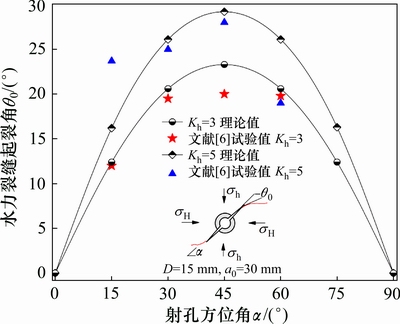
图7 水力裂缝起裂角θ0的试验值与理论值对比
Fig. 7 Comparison of initiation angle θ0 between theoretical and experimental results
由图7可知:除Kh=3, =45°和Kh=5,
=45°和Kh=5, =15°时起裂角θ0的试验值偏离理论值以外,其余情况下的射孔尖端水力裂缝的起裂角θ0与JIN[6]所测试验值吻合较好,其相对误差不大。因此水力裂缝起裂角θ0的理论值基本符合模型试验值。
=15°时起裂角θ0的试验值偏离理论值以外,其余情况下的射孔尖端水力裂缝的起裂角θ0与JIN[6]所测试验值吻合较好,其相对误差不大。因此水力裂缝起裂角θ0的理论值基本符合模型试验值。
2.2 实际工程值与理论值对比
以渤海某油井[22]为研究对象,该油井井筒直径D=178 mm;取射孔长度a0=356 mm,该长度为井筒直径D的2倍;水平地应力分别为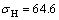 MPa和
MPa和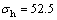 MPa,由式(23)可得水平应力差Kh=0.23。该油井参数如表2所示。
MPa,由式(23)可得水平应力差Kh=0.23。该油井参数如表2所示。
表2 渤海某油井参数[22]
Table 2 Parameters of an oil well in Bohai[22]
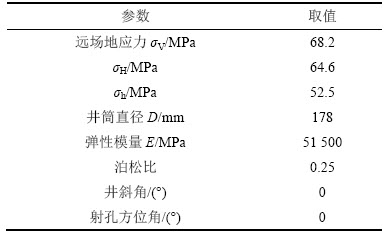
该井的实测地层破裂压力Pb为58.3 MPa。将表2中参数代入本文的理论方法,可得射孔尖端的水力裂缝起裂角θ0为0°,地层破裂压力Pb为54.9 MPa。
由于射孔方位角为0°,射孔轴线沿着最大水平地应力方向,此时水力裂缝呈纯Ⅰ型,因此起裂角θ0恒为0°且符合工程实际。此外,定义理论值与工程实际值之间的相对误差为
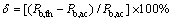 (24)
(24)
式中:△为相对误差;Pb,th和Pb,ac分别为地层破裂压力理论值和实测值。
根据式(24)可求得相对误差仅为5.85%,基本符合工程实测值。
3 射孔对地层破裂压力的影响
射孔作为压裂液通道[1],在压裂过程中具有1) 调节破裂压力Pb;2) 控制水力裂缝的初始方位;3) 调整储层间液体流量等作用。因此,有必要从理论上研究不同射孔参数对地层破裂压力Pb和水力裂缝起裂角θ0的影响。射孔参数主要射孔密度、射孔直径、射孔方位角和射孔长度。本文采用2D井筒-射孔模型,因此,只研究射孔长度a0和方位角 对破裂压力压力Pb和起裂角度θ0的影响。
对破裂压力压力Pb和起裂角度θ0的影响。
3.1 射孔方位角的影响
在水力压裂过程中,选择合理的射孔角度[23]可以确保:1) 水力裂缝总是沿垂直于最小水平主应力方向延伸;2) 裂缝宽度足够大;3) 单一主裂缝向地层远处发展;4) 避免裂缝转向;5) 降低地层破裂压力。
本文选取井筒直径D=15 mm,取射孔长度a0为井筒直径D的2倍,即a0=30 mm;水平最大、最小地应力分别为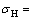 6 MPa和
6 MPa和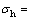 1 MPa,水平应力差Kh=5;射孔方位角
1 MPa,水平应力差Kh=5;射孔方位角 取0°~90°,射孔端部产生水力裂缝时的地层破裂压力如图8所示。为了研究射孔方位角对地层破裂压力的影响,定义压力变化量
取0°~90°,射孔端部产生水力裂缝时的地层破裂压力如图8所示。为了研究射孔方位角对地层破裂压力的影响,定义压力变化量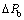 为
为
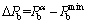 (25)
(25)
式中: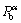 为射孔方位角为
为射孔方位角为 时的地层破裂压力;
时的地层破裂压力;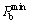 为所有结果中的最小破裂压力。
为所有结果中的最小破裂压力。
由图8可知:射孔方位角 越大,地层破裂压力Pb也逐渐增大。当射孔方位角
越大,地层破裂压力Pb也逐渐增大。当射孔方位角 =0°时,射孔轴线沿着最大水平地应力方向。此时射孔轴线上的地应力分量恒为0 MPa,且沿垂直于射孔轴线方向上的地应力分量为最小值
=0°时,射孔轴线沿着最大水平地应力方向。此时射孔轴线上的地应力分量恒为0 MPa,且沿垂直于射孔轴线方向上的地应力分量为最小值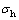 ,因此地层破裂压力Pb最小。这表明射孔的破坏满足最小能量原理, 即储层岩体总是沿着能量消耗最小的方向破裂。当射孔方位角
,因此地层破裂压力Pb最小。这表明射孔的破坏满足最小能量原理, 即储层岩体总是沿着能量消耗最小的方向破裂。当射孔方位角 =90°时,沿垂直于射孔轴线上的地应力分量最大,储层岩石破裂时所需的压裂液压力也应最大,因此,地层破裂压力Pb最大。
=90°时,沿垂直于射孔轴线上的地应力分量最大,储层岩石破裂时所需的压裂液压力也应最大,因此,地层破裂压力Pb最大。
由压力变化△Pb可得,不同射孔方位角 下的地层破裂压力Pb主要呈现4阶段:
下的地层破裂压力Pb主要呈现4阶段:
1) 当 =0°~15°时,地层破裂压力Pb无明显变化,其变化幅度△Pb在0~0.07 MPa之间;此时射孔方位角
=0°~15°时,地层破裂压力Pb无明显变化,其变化幅度△Pb在0~0.07 MPa之间;此时射孔方位角 对地层破裂压力Pb的影响不明显。
对地层破裂压力Pb的影响不明显。
2) 当 =15°~35°时,地层破裂压力Pb缓慢增长,其变化幅度△Pb在0.5 MPa以内。
=15°~35°时,地层破裂压力Pb缓慢增长,其变化幅度△Pb在0.5 MPa以内。
3) 当 =35°~80°时,地层破裂压力Pb快速增长,其变化幅度△Pb在4.72 MPa;因此,不合理的射孔方位角将极大的增加地层破裂时射孔内的压裂液压力,甚至造成压裂失败。
=35°~80°时,地层破裂压力Pb快速增长,其变化幅度△Pb在4.72 MPa;因此,不合理的射孔方位角将极大的增加地层破裂时射孔内的压裂液压力,甚至造成压裂失败。
4) 当 =80°~90°时,地层破裂压力Pb的增长趋于平缓。
=80°~90°时,地层破裂压力Pb的增长趋于平缓。
可见,最优射孔方位角 应该在0°~15°的范围内。ABASS等[24]指出:80°相位布孔且射孔方位和最优起裂面成30°夹角,即可保证射孔和地层水力裂缝具有良好的连通性,避免多裂缝和裂缝弯曲,并增加裂缝宽度。BEHRMANN等[4]研究表明:孔方位角位于最优起裂面20°的范围内有利于裂缝扩展;陈峥嵘等[22]认为:最佳的射孔方位角应在15°范围以内。因此,本文的理论结果与文献结果具有一致性。
应该在0°~15°的范围内。ABASS等[24]指出:80°相位布孔且射孔方位和最优起裂面成30°夹角,即可保证射孔和地层水力裂缝具有良好的连通性,避免多裂缝和裂缝弯曲,并增加裂缝宽度。BEHRMANN等[4]研究表明:孔方位角位于最优起裂面20°的范围内有利于裂缝扩展;陈峥嵘等[22]认为:最佳的射孔方位角应在15°范围以内。因此,本文的理论结果与文献结果具有一致性。
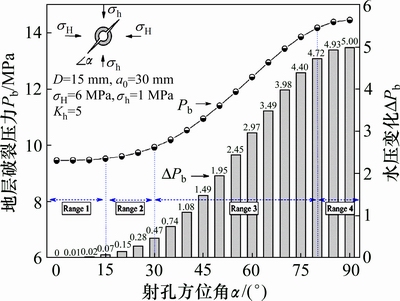
图8 地层破裂压力Pb与射孔方位角α的关系
Fig. 8 Relationship between break down pressure Pb and perforation azimuth α
3.2 射孔长度的影响
在钻井过程中,储层岩石污染带厚度在1 m以上,严重污染的厚度范围为300~500 mm。因此,合理的射孔长度有利于穿过近井污染区,减小井筒近井效应对水力裂缝起裂扩展的影响,并有利于降低地层破裂压力[25]。因此,有必要从理论上研究射孔长度对破裂压力Pb的影响。
选取井筒直径D=15 mm,最大和最小水平地应力分别为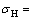 6 MPa和
6 MPa和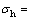 1 MPa,即水平应力差Kh=5;射孔方位角
1 MPa,即水平应力差Kh=5;射孔方位角 为15°。射孔长度a0为井筒直径D的0.4~6.0 倍。地层破裂压力Pb的理论结果如图9所示。
为15°。射孔长度a0为井筒直径D的0.4~6.0 倍。地层破裂压力Pb的理论结果如图9所示。
由图9可知:随着射孔长度a0的不断增加,地层破裂压力Pb逐渐减小。当射孔相对长度a0/D = 0.4时,地层破裂压力Pb=15.99 MPa;当射孔相对长度a0/D=6.0时,地层破裂压力Pb=6.16 MPa,与a0/D=0.4时相比,减少了9.83 MPa。HALLAM等[3]指出无射孔完井的水力裂缝的起裂方位具有随机性。但由于射孔的存在,射孔尖端存在应力集中现象,且射孔长度a0越长,应力集中现象越明显,因此压裂储层岩石所需的压力就会越小。结果表明,射孔长度a0对地层破裂压力Pb的影响显著。
由破裂压力变化量△Pb可得,不同射孔相对长度a0/D下的地层破裂压力Pb主要呈现3个阶段:
1) 当a0/D小于2时,地层破裂压力Pb迅速减小。射孔长度a0由0.4D增长到 2D时,压力递减幅度△Pb为6.46 MPa左右。
2) 当a0/D为2~5之间时,地层破裂压力Pb缓慢减小且呈线性递减。射孔长度a0由2D增加到5D时,压力递减幅度为3 MPa左右。
3) 当a0/D大于5时,地层破裂压力Pb变化幅度不大,其值趋向于最大地层压力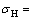 6 MPa。因此,当射孔长度足够长时,射孔长度对地层破裂压力Pb的影响较小。
6 MPa。因此,当射孔长度足够长时,射孔长度对地层破裂压力Pb的影响较小。
在实际工程中,常规射孔击穿深度最大可达800 mm,一般为400 mm左右。而井筒直径一般为180 mm左右,则射孔长度a0一般是井筒直径D的2~3倍[25]。此外,射孔需要穿越近井污染区,因此,本文建议最优射孔长度a0应为井筒直径D的2~3倍,与张广清等[11]的数值模拟规律基本一致。

图9 地层破裂压力Pb与射孔长度a0的关系
Fig. 9 Relationship between break down pressure Pb and perforation length a0
3.3 主应力差的影响
陈勉等[26]指出地层的围压来源于非均匀的原地应力场,若垂向应力源于地层自重,则应力梯度平均为 0.023 MPa/m,多数地区最大水平应力往往大于垂向应力,且2个水平地应力梯度的比值达1.4~1.5。在山前构造带地区,不但地应力梯度高,最大和最小水平地应力的比值也很大。因此,有必要研究主应力差对地层破裂压力的影响。
选取井筒直径D=15 mm,射孔长度a0为井筒直径D的2倍。射孔方位角 取0°~90°,最小地应力取
取0°~90°,最小地应力取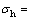 1 MPa,最大地应力
1 MPa,最大地应力 分别取 2,3,4,5和6 MPa,即水平应力差Kh分别为1,2,3,4和5。地层破裂压力的理论计算结果如图10所示。
分别取 2,3,4,5和6 MPa,即水平应力差Kh分别为1,2,3,4和5。地层破裂压力的理论计算结果如图10所示。
由图10可得:水平应力差Kh越大,射孔端部破裂时所需要的地层破裂压力Pb也越大;当Kh=1时,随着射孔方位角 的增加,地层破裂压力仅缓慢增长,涨幅仅在0.5 MPa 左右;但当Kh=5时,随着射孔方位角
的增加,地层破裂压力仅缓慢增长,涨幅仅在0.5 MPa 左右;但当Kh=5时,随着射孔方位角 的增加,地层破裂压力急剧增加,涨幅5 MPa左右;此外,当射孔方位角
的增加,地层破裂压力急剧增加,涨幅5 MPa左右;此外,当射孔方位角 介于0°~30°之间时,无论Kh为何值,地层破裂压力Pb无明显变化;当
介于0°~30°之间时,无论Kh为何值,地层破裂压力Pb无明显变化;当 大于30°时,Kh对地层破裂压力Pb的影响十分显著。因此,在实际工程中应力梯度较大储层中,Kh对地层破裂压力的影响十分明显,此时,更应当精确地控制射孔方位角的范围。
大于30°时,Kh对地层破裂压力Pb的影响十分显著。因此,在实际工程中应力梯度较大储层中,Kh对地层破裂压力的影响十分明显,此时,更应当精确地控制射孔方位角的范围。
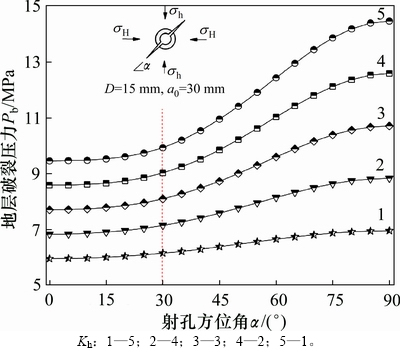
图10 地层破裂压力Pb与主应力差Kh的关系
Fig. 10 Relationship between break down pressure Pb and dimensionless principal stress difference Kh
4 射孔对裂缝起裂角的影响
李根生等[23]指出水力压裂过程中,水力裂缝首先在射孔端部附近的拉应力区起裂,在近井区域产生裂缝转向,最终趋于最大主应力方向。因此,水力裂缝起裂角θ0是近井区域裂缝转向的重要参数。本文主要研究主应力差Kh、射孔方位角 和射孔长度a0对水力裂缝起裂角θ0的影响。
和射孔长度a0对水力裂缝起裂角θ0的影响。
4.1 主应力差和射孔方位角的影响
选取井筒直径D=15 mm,射孔长度a0=30 mm。射孔方位角 取0°~90°,最小水平地应力为
取0°~90°,最小水平地应力为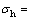 1 MPa,最大水平地应力
1 MPa,最大水平地应力 分别为 2,3,4,5和6 MPa,即水平应力差Kh分别为1,2,3,4和5。射孔端部水力裂缝起裂角θ0的理论值如图11所示。
分别为 2,3,4,5和6 MPa,即水平应力差Kh分别为1,2,3,4和5。射孔端部水力裂缝起裂角θ0的理论值如图11所示。

图11 水力裂缝起裂角θ0与主应力差Kh的关系
Fig. 11 Relationship between initiation angle θ0 and dimensionless principal stress difference Kh
由图11可知:当射孔方位角 =0°或者90°时,射孔轴线方向的地应力分量恒为0,井筒和射孔内的压裂液压力只需克服射孔表面的正压力和储层岩石本身的抗拉强度,此时,射孔端部的水力裂缝处于纯Ⅰ型,因此,起裂角θ0恒为0°,裂缝起裂后沿着射孔轴线形成单一主裂缝向地层远处发展;当射孔方位角
=0°或者90°时,射孔轴线方向的地应力分量恒为0,井筒和射孔内的压裂液压力只需克服射孔表面的正压力和储层岩石本身的抗拉强度,此时,射孔端部的水力裂缝处于纯Ⅰ型,因此,起裂角θ0恒为0°,裂缝起裂后沿着射孔轴线形成单一主裂缝向地层远处发展;当射孔方位角 接近0°或者90°时,水力裂缝起裂角θ0较小,因此裂缝起裂后将在近井区域易形成较小曲率的裂缝;如此有利于降低注入压力和流动阻力,从而易形成长而宽的裂缝;当射孔方位角
接近0°或者90°时,水力裂缝起裂角θ0较小,因此裂缝起裂后将在近井区域易形成较小曲率的裂缝;如此有利于降低注入压力和流动阻力,从而易形成长而宽的裂缝;当射孔方位角 =45°时,射孔轴线方向的地应力分量最大,此时射孔端部水力裂缝处于Ⅰ-Ⅱ复合型,裂缝的起裂需要同时克服射孔轴线和垂直于射孔轴线方向的地应力分量以及岩石本身的抗拉强度,此时,水力裂缝的起裂角θ0最大,易形成较大曲率的裂缝;当压裂液在其中流动时,会产生较大的摩擦阻力与压降损失,不利于流体流动与压力传导,其结果可能导致支撑剂沉降、砂堵,甚至造成压裂失败[23]。
=45°时,射孔轴线方向的地应力分量最大,此时射孔端部水力裂缝处于Ⅰ-Ⅱ复合型,裂缝的起裂需要同时克服射孔轴线和垂直于射孔轴线方向的地应力分量以及岩石本身的抗拉强度,此时,水力裂缝的起裂角θ0最大,易形成较大曲率的裂缝;当压裂液在其中流动时,会产生较大的摩擦阻力与压降损失,不利于流体流动与压力传导,其结果可能导致支撑剂沉降、砂堵,甚至造成压裂失败[23]。
此外,无论水平应力差Kh为何值,射孔方位角 =0°或者90°时水力裂缝的起裂角θ0恒为0°;当
=0°或者90°时水力裂缝的起裂角θ0恒为0°;当 ≠0°或者
≠0°或者 ≠90°时,水平应力差Kh越大,射孔轴线方向的地应力分量就越大,Ⅱ型裂缝的剪切效应越明显,因此水力裂缝的起裂角θ0越大。因此,对于应力梯度较大的储层,更应严格控制射孔方位角
≠90°时,水平应力差Kh越大,射孔轴线方向的地应力分量就越大,Ⅱ型裂缝的剪切效应越明显,因此水力裂缝的起裂角θ0越大。因此,对于应力梯度较大的储层,更应严格控制射孔方位角 ,从而形成宽而长的水力裂缝。
,从而形成宽而长的水力裂缝。
4.2 射孔长度的影响
本文选取井筒直径D=15 mm,射孔方位角 为15°,最小水平地应力取
为15°,最小水平地应力取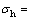 1 MPa,最大水平地应力
1 MPa,最大水平地应力 分别取 2,4和6 MPa,即水平应力差Kh分别为1,3和5;取射孔长度a0为井筒直径D的0.4~6.0倍。射孔端部水力裂缝起裂角θ0的理论值如图12所示。
分别取 2,4和6 MPa,即水平应力差Kh分别为1,3和5;取射孔长度a0为井筒直径D的0.4~6.0倍。射孔端部水力裂缝起裂角θ0的理论值如图12所示。
由图12可知:当射孔相对长度a0/D小于1时,水力裂缝起裂角θ0快速增加;当射孔相对长度a0/D大于1后,起裂角θ0呈线性增长。当水平应力差Kh较小时,射孔长度a0对水力裂缝起裂角θ0的影响不大,起裂角θ0均在10°以内;当水平应力差Kh较大时,射孔长度a0对起裂角有显著影响,起裂角θ0从5°增加到25°。
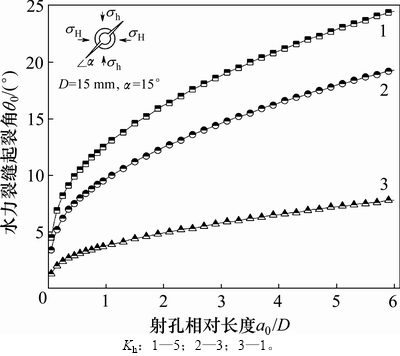
图12 水力裂缝起裂角θ0与射孔长度a0的关系
Fig. 12 Relationship between initiation angle θ0 and perforation length a0
5 结论
1) 随着射孔方位角 从0°增加到90°,地层破裂压力Pb开始保持不变,然后缓慢增加,接着快速增长,最后趋于平缓。建议最佳射孔方位角
从0°增加到90°,地层破裂压力Pb开始保持不变,然后缓慢增加,接着快速增长,最后趋于平缓。建议最佳射孔方位角 应为0°~15°。
应为0°~15°。
2) 随着射孔长度a0的增加,地层破裂压力Pb逐渐降低。基于本文计算结果,并充分考虑射孔弹有效射程和近井污染区半径的条件下,本文认为最佳射孔长度应该在2~3倍井筒直径之间。
3) 水力裂缝的起裂角随主应力差、射孔长度和射孔角度的增大而增大。
参考文献:
[1] 刘合, 王峰, 王毓才, 等. 现代油气井射孔技术发展现状与展望[J]. 石油勘探与开发, 2014, 41(6): 731-737.
LIU He, WANG Feng, WANG Yucai, et al. Oil well perforation technology: Status and prospects[J]. Petroleum exploration and development, 2014, 41(6): 731-737.
[2] SOLIMAN M Y. Interpretation of pressure behavior of fractured, deviated, and horizontal wells[C]// Proceedings of the 1990 Easten Regional Conference and Exhibition. Columbus, 1990: 7-15.
[3] HALLAM S D, LAST N C. Geometry of hydraulic fractures from modestly deviated wellbores[J]. Journal of Petroleum Technology, 1991, 43(6): 742-748.
[4] BEHRMANN L A, ELBEL J L. Effect of perforations on fracture initiation[J]. Journal of Petroleum Technology, 1991, 43(5): 608–615.
[5] VAN D R G, PATER C J. Experimental study on the impact of perforations on hydraulic fracture tortuosity[C]// Proceeding of European Formation Damage Conference. Richardson: SPE, 1997: 65-73.
[6] JIN X. An integrated geomechanics and petrophysics study of hydraulic fracturing in naturally fractured reservoirs[D]. Oklahoma: the University of Oklahoma. Engineering Petroleum, 2014: 80-81.
[7] 姜浒, 陈勉, 张广清, 等, 定向射孔对水力裂缝起裂与延伸的影响[J]. 岩石力学与工程学报, 2009, 28(7): 1321-1326.
JIANG Hu, CHEN Mian, ZHANG Guangqing, et al. Impact of oriented perforation on hydraulic fracture initiation and propagation[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(7): 1321-1326.
[8] 门晓溪, 唐春安, 韩志辉, 等. 射孔角度对水力压裂裂纹扩展影响数值模拟[J]. 东北大学学报(自然科学版), 2013, 34(11): 1638-1641.
MEN Xiaoxi, TANG Chun’an, HAN Zhihui, et al. Numerical simulation to influence of perforation angle on fracture propagation under hydraulic fracturing[J]. Journal of Northeastern University, 2013, 34(11): 1638-1641.
[9] 彪仿俊, 刘合, 张劲, 等. 螺旋射孔条件下地层破裂压力的数值模拟研究[J]. 中国科学技术大学学报, 2011, 41(3): 219-226.
BIAO Fangjun, LIU He, ZHANG Jin, et al. A numerical study of fracture initiation pressure under helical perforation conditions[J]. Journal of University of Science and Technology of China, 2011, 41(3): 219-226.
[10] 王素玲, 董康兴, 董海洋. 低渗透储层射孔参数对起裂压力的影响[J]. 石油钻采工艺, 2009, 31(3): 85-89.
WANG Suling, DONG Kangxing, DONG Haiyang. Effect analysis of perforating parameters upon initiation pressure in low permeability reservoir[J]. Oil Drilling & Production Technology, 2009, 31(3): 85-89.
[11] 张广清, 殷有泉, 陈勉, 等. 射孔对地层破裂压力的影响研究[J]. 岩石力学与工程学报, 2003, 22(1): 40-44.
ZHANG Guangqing, YIN Youquan, CHEN Mian, et al. Influence of perforation on formation fracturing pressure[J]. Chinese Journal of Rock Mechanics & Engineering, 2003, 22(1): 40-44.
[12] YEW C H, SCHMIDT J H, LI Y. On fracture design of deviated wells[C]// Proceedings of SPE Annual Technical Conference and Exhibition. San Antonio, TX, USA: Society of Petroleum Engineers of AIME, 1989: 211-224.
[13] HOSSAIN M, RAHMAN M, RAHMAN S. A comprehensive monograph for hydraulic fracture initiation from deviated wellbores under arbitrary stress regimes[C]// SPE Asia Pacific Oil and Conference and Exhibition, Jakarta, Indonesia: Society of Petroleum Engineers, 1999: 54360-MS.
[14] 唐世斌, 刘向君, 罗江, 等. 水压诱发裂缝拉伸与剪切破裂的理论模型研究[J]. 岩石力学与工程学报, 2017, 36(9): 2124-2135.
TANG Shibin, LIU Xiangjun, LUO Jiang, et al. Theoretical model for tensile and shear crack initiation at the crack tip in rock subjected to hydraulic pressure[J]. Chinese Journal of Rock Mechanics & Engineering, 2017, 36(9): 2124-2135.
[15] TADA H, PARIS P C, IRWIN G R. The stress analysis of cracks handbook[M]. New York: ASME Press, 2000: 614-615.
[16] 徐芝纶. 弹性力学[M]. 北京: 高等教育出版社, 2006: 88-115.
XU Zhilun. Elasticity[M]. Beijing: Higher Education Press, 2006: 88-115.
[17] ZHU Z. New Biaxial failure criterion for brittle materials in compression[J]. Journal of Engineering Mechanics, 1999, 125(11): 1251-1258.
[18] FAN Y, ZHU Z, KANG J, et al. The mutual effects between two unequal collinear cracks under compression[J]. Mathematics & Mechanics of Solids, 2016, 22(5): 1-14.
[19] ZHU Z. An alternative form of propagation criterion for two collinear cracks under compression[J]. Mathematics & Mechanics of Solids, 2009, 14(8): 727-746.
[20] 郭俊宏, 刘官厅. 带双裂纹的椭圆孔口问题的应力分析[J]. 力学学报, 2007, 39(5): 699-703.
GUO Junhong, LIU Guanting. The stress analysis of an elliptical hole with double cracks[J]. Chinese Journal of Theoretical and Applied Mechanics, 2007, 39(5): 699-703.
[21] RENSHAW C, POLLARD D D. Are large differential stresses required for straight fracture propagation paths[J]. Journal of Structural Geology, 1994, 16(6): 817-822.
[22] 陈峥嵘, 邓金根, 朱海燕, 等. 定向射孔压裂起裂与射孔优化设计方法研究[J]. 岩土力学, 2013, 34(8): 2309-2315.
CHEN Zhengrong, DENG Jingen, ZHU Haiyan, et al. Research on initiation of oriented perforation fracturing and perforation optimization design method[J]. Rock and Soil Mechanics, 2013, 34(8): 2309-2315.
[23] 李根生, 黄中伟, 牛继磊, 等. 地应力及射孔参数对水力压裂影响的研究进展[J]. 中国石油大学学报, 2005, 29(4): 136-142.
LI Gensheng, HUANG Zhongwei, NIU Jilei, et al. Research advance of the influence of geostress and perforation parameters on hydraulic fracturing[J]. Journal of the University of Petroleum China, 2005, 29(4): 136-142.
[24] ABASS H H, MEADOWS D L, BRUMLEY J L, et al. Oriented perforations: a rock mechanics view[C]// Proceedings of the 9th Middle East Oil Show & Conference. Richardson, TX: Society of Petroleum Engineers (SPE), 1995: 13-27.
[25] 周再乐, 张广清, 熊文学, 等. 水平井限流压裂射孔参数优化[J]. 断块油气田, 2015, 22(3): 374-378.
ZHOU Zaile, ZHANG Guangqing, XIONG Wenxue, et al. Perforating parameter optimization of limit entry fracturing for horizontal wells[J]. Fault-Block Oil and Gas Field, 2015, 22(3): 374-378.
[26] 陈勉, 金衍, 张广清. 石油工程岩石力学[M]. 北京: 科学出版社, 2008: 2-3.
CHEN Mian, JIN Yan, ZHANG Guangqing. Petroleum engineering rock mechanics[M]. Beijing: Science Press, 2008: 2-3.
(编辑 赵俊)
收稿日期:2018-05-15;修回日期:2018-08-26
基金项目(Foundation item):国家自然科学基金资助项目(11672194,11702181);四川省安全监管局安全生产科技项目(aj20170515161307);四川省科技计划项目(2018JZ0036) (Projects(11672194, 11702181) supported by the National Natural Science Foundation of China; Project (aj20170515161307) supported by Sichuan Administration of Work Safety; Project(2018JZ0036) supported by Science and Technology of Sichuan Province)
通信作者:朱哲明,博士,教授,博士生导师;从事岩石力学与采矿工程研究;E-mail:zhemingzhu@hotmail.com